Complete Solutions to Exercises of chapter CENTER OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTER OF MASS |
| CP SINGH | Exercises |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Two blocks of mass `1kg` and `3 kg` have position v ectors ` hat(i) + 2 hat(j) + hat(k)` and `3 hat(i) - 2 hat(j) + hat(k)` , respectively . The center of mass of this system has a position vector.
View SolutionAll the particles of a body situated at distance `d` from the origin. The distance of the center of mass of the body from the origin is
View SolutionParticle of masses `m, 2m,3m,…,nm` grams are placed on the same line at distance `l,2l,3l,…..,nl cm` from a fixed point. The distance of centre of mass of the particles from the fixed point in centimeters is :
View SolutionThree identical metal balls each of radius `r` are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three balls are joined. The center of mass of system is located at the
View SolutionLook at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6 m. The coordinates of the centres of the different parts are: outer cicle (0,0), left circle (-a, a), right inner circle (a,a), vertical line (0,0) and horizontal line (0 ,-a). The y-coordinate of the centre of mass of the ink in this drawing is

View SolutionA circular disc of radius `R` is removed from a bigger circular disc of radius `2 R` such that the circumferences of the discs coincide. The center of mass of new disc is `alpha R` from the center of the bigger disc. The value of `alpha` is
View SolutionA hemisphere and a solid cone have a common base. The center of mass of common structure coincides with the common base. If `R` is the radius of hemisphere and `h` is the height of the cone, then `h//R` will be
View SolutionIf the linear density (mass per unit length) of a rod of length `3 m` is proportional to `x`, where `x`, where `x` is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is.
View SolutionThe mass per unit length of a non - uniform rod of length `L` is given `mu = lambda x^(2)` , where `lambda` is a constant and `x` is distance from one end of the rod. The distance of the center of mas of rod from this end is
View SolutionA thin rod of length 'L' is lying along the x-axis with its ends at x=0 and x=L its linear (mass/length) varies with `x as k((x)/(L))^n`, where n can be zero of any positive number. If to position `x_(CM)` of the centre of mass of the rod is plotted against 'n', which of the following graphs best apporximates the dependence of `x_(CM)` on n?
View SolutionWhich of the following is true for center of mass ?
(i) The center of mass of a body may lie within , outside , on the surface of the body.
(ii) In the case of symmetrical bodies , the center of mass coincides with the geometrical center of the body.
(iii) In the absence of external forces , the center of mass moves with constant velocity.
(iv) If external forces are absent and system is initially at rest, then location of center of mass is fixed.
View SolutionA cubical block of ice of maas m and edge L is placed in a large tray of maas M. If the ie melts, how far does the centre of maas of the system ''ice plus tray'' come down?
View SolutionTwo paricle A and B initially at rest, move towards each other under mutual force of attraction. At the instant when the speed of A is V and the speed of B is 2V, the speed of the centre of mass of the system is
View SolutionA ladder is leaned against a smooth wall and it is allowed to slip on a frictionless floor. Which figure represents the track of its centre of mass ?
View SolutionA pulley fixed to the ceiling carries a string with blocks of mass `m` and `3m` attached to its ends. The masses of string and pulley are negligible .When the system is released, its center of mass moves with what acceleration
View SolutionTwo balls are thrown simultaneously from top of tower in air as shown in the figure.
(i) The acceleration of the center of mass of two balls while in air is equal to `g`.
(ii) The path followed by the center of mass is parabola.
(iii) The path followed by the center of mass will change if one ball after striking the ground comes to rest.
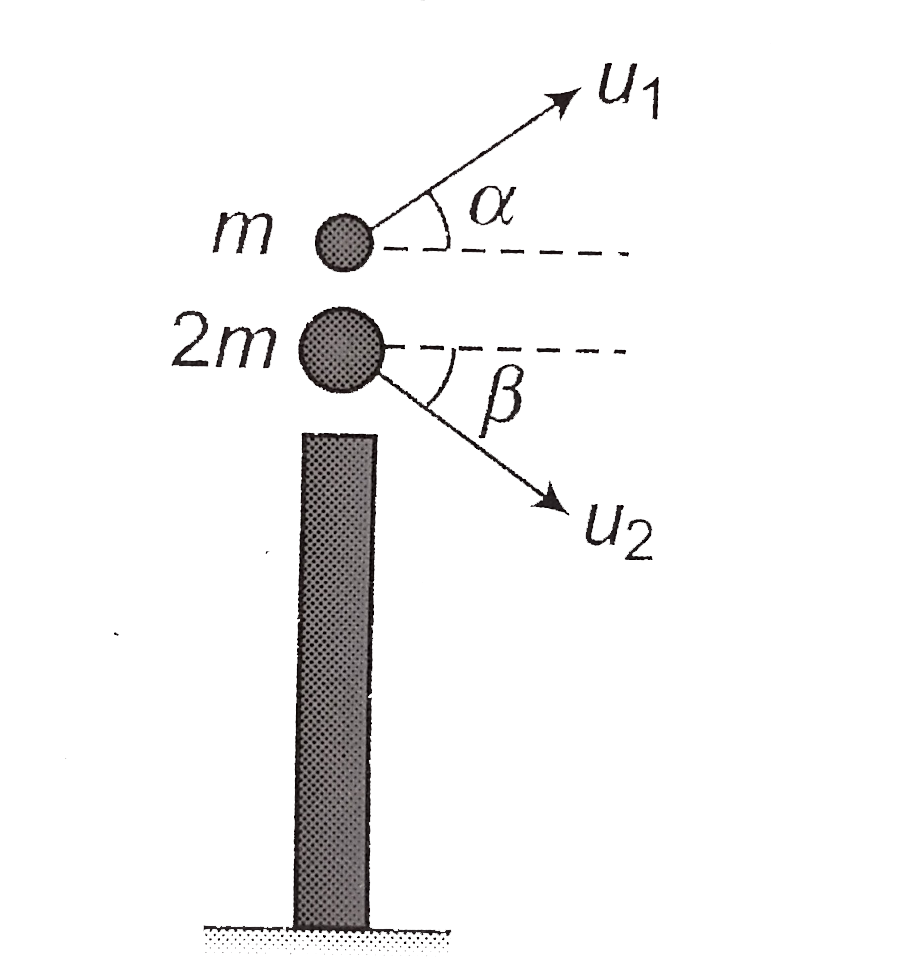
View SolutionWhich of the following statements are true ?
(i) A uniform wooden plank of mass `150 kg` and length `8 m` is floating on still water with a man of `50 kg` at one end of it. The man walks to the other end of the plank and stops. The distance covered by the plank is `2 m`.
(ii) A kid of mass `15 kg` is sitting in a boat of mass `45 kg` in a lake. The distance of kid from the bank of lake is `12 m`. Now the body moves inside the boat at a distance `4m` towards the bank and stops. The distance of the kid from the bank (there is no friction between the water and the boat ) is `11 m`.
(iii) Two persons of masses `40 kg` and `60 kg` are sitting at the midpoint of a `12 -m`- long boat `(140 kg)` standing still in water. Now they move to opposite ends of the boat. Neglecting the friction between boat and water, the distance traveled by the boat in water is `50 cm`.
(iv) In a gravity free space , a man of mass `m` standing at a height `h` above the floor, throws a ball of mass `m_(0)` straight down with a speed `v_(0)`. When the ball reaches the floor, the distance of the man above the floor is `(1 + (m_(0))/(m))h`.
View SolutionWhich of the following statements is true ?
(i) A car of mass `M` is tied by one end of a massless rope of length `10 m`. The other end of the rope is in the hands of a man of mass `M`. The entire system is on a smooth horizontal surface.The man is at `x = 0` and the cart at `x = 10 m`. If the man pulls the cart by the rope, the man and the cart will meet at the point `x = 5 m`.
(ii) Two spherical bodies of mass `M` and `5 M` and radii `R` and `2 R`, respectively , are released in free space with initial separation between their centers equal to `12 R`. If they attract each other due to the gravitational force only , then the distance covered by the smaller body just before collision is `7.5 R`.
(iii) Two skaters `A` and `B` , having masses `40 kg` and `60 kg` , respectively stand facing each other `10 m` apart on a horizontal smooth surface. They pull on a rope stretched between them , the distance covered by `A`, when skaters meet is `6 m`.
(iv) A ballon (mass M) is attached to light rope of length `L`. To the other end of the rope a boy (mass m) is hanging in air. The system is at rest. The distance travelled by the balloon (in downward direction) when the boy touches the ballon is `(ML)/(M + m)`.
View SolutionA boy of mass `40 kg` stands on a rail road car of mass `60 kg`, moving with velocity `10 m//s`. Now , the boy begins to run with velocity `5 m//s` , with respect to the car , in the same direction , the velocity of the car will be
View SolutionA boy `(mass of 40 kg)` is standing at one end of a boat (mass of 60 kg) in still water. The length of the boat is `10 m` and the boy takes `2s` to reach at other end of boat moving with constant speed. Assuming no friction between the boat and the water.
(i) The distance covered by the boat is `4 m`
(ii) The distance covered by the boy with respect to the ground is `6 m`.
(iii) The velocity of the boy with respect to the ground is `lt 5 m//s`
(iv) The velocity of the boy is `3 m//s`
View SolutionTwo particles `A` and `B` of masses `2m` and `m` are placed on a smooth surface at separation `d`. They move towards each other due to the mutual attractive force.
(i) The particles will meet at distance `d//3` from the initial position of mass `2m`.
(ii) The speed of `A` will be half of speed of `B` until the particles collide (excluding the initial speed).
(iii) The distance covered by `B` is always double that covered by `A` until the particles collide.
(iv) The velocity of center of mass is always zero.
View SolutionA wooden plank of mass `M` and length `L` is floating in still water. A persons of mass `m` starts at one end of the plank and reaches to other end other end in time `t_(0)`, moving with a constant speed. Choose the correct option.
(i) The speed of the person as seen from the ground is smaller than `(L)/(t_(0))`.
(ii) The speed of the plank as seen from the ground is `((m)/(m + M)) (L)/(t_(0))`.
(iii) The speed of the plank as seen from the ground is `((M)/(m + M))(L)/(t_(0))`.
(iv) The total `K.E.` of the system is `(1)/(2) (m + M)((L)/(t_(0)))^(2)`.
View SolutionThemasses of `1g` and `4g` are moving with equal kineticc energies. Calculate the ration of the magnitudes of their linear momenta.
View SolutionTwo bodies with kinetix energies in the ratio of `4 : 1` are moving with equal linear momentum. The ratio of their masses is
View SolutionIf KE of a body increases by `300%`, by what `%` will the linear momentum of the body increase?
View SolutionIf the kinetic energy of a body increases by `0.1 %` the percent increase of its momentum will be
View SolutionA body of mass `0.5 kg` is projected under the gravity with a speed of `98 m//s` at an angle of `30^(@)` with the horizontal. The change in momentum (in magnitude) of the body when it strikes the ground is
View SolutionA paticle of mass `m` is executing uniform circular motion on a path of radius `r`. If `p` is the magnitude of its linear momentum, then the radial force acting on the particle is
View SolutionA ball of mass `m` falls vertically to the ground from a height `h_1` and rebound to a height `h_2`. The change in momentum of the ball on striking the ground is.
View SolutionA particle of mass `M` is moving in a horizontal circle of radius `R` with uniform speed `V`. When it moves from one point to a diametrically opposite point , its
View SolutionA particle moves in the X-Y plane under the influence of a force such that its linear momentum is `oversetrarrp(t)=A[haticos(kt)-hatjsin(kt)]`, where A and k are constants. The angle between the force and the momentum is
View SolutionConsider the following two statements:
A. Linear momentum of a system of partcles is zero.
B. Kinetic energ of a system of particles is zero.
View SolutionConsider the following two statements :
1. Linear momentum of a system of particles is zero
2. Kinetic energy of a system of particles is zero , Then
View SolutionA stationary partical explodes into two partical of a masses `m_(1) and m_(2)` which move in opposite direction with velocities `v_(1) and v_(2)`. The ratio of their kinetic energies `E_(1)//E_(2)` is
View SolutionA shell of mass `20 kg` at rest explodes into two fragments whose masses are in the ratio `2 : 3`. The smaller fragment moves with a velocity of `6 m//s`. The kinetic energy of the larger fragment is
View SolutionA bomb of mass `3.0 kg` explodes in air into two pieces of masses `2.0 kg` and `1.0 kg`. The total energy imparted to the two fragment is
View SolutionA bomb of mass `9 kg` explodes into `2` pieces of mass `3 kg` and `6 kg`. The velocity of mass `3 kg is 1.6 m//s`. The `K.E. of mass 6 kg` is
View SolutionA shell of mass `200g` is ejected from a gun of mass `4 kg` by an explosion that generate `1.05 kJ` of energy. The initial velocity of the shell is
View SolutionA body of mass `50 kg` is projected vertically upward with velocity of `100 m//s`. After `5 s` this body breaks into `20 kg` and `30 kg`. If the `20 kg` piece travels upwards with `150 m//s`, then the velocity of other block will be
View SolutionA shell is fired from a cannon with a velocity `v (m//sec.)` at an angle `theta` with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon and the speed (in `m//sec.`) of the other piece immediately after the explosion is
View SolutionAt high altitude , a body explodes at rest into two equal fragments with one fragment receiving horizontal velocity of `10 m//s`. Time taken by the two radius vectors connecting of explosion to fragments to make `90^(@)` is
View SolutionA bomb explodes in air when it has a horizontal speed of `10 m//s`. It breaks into two pieces `A` and `B` of mass ratio `1 : 2`. If `A` goes vertically up at a speed of `40 m//s` , the speed of `B` is
View SolutionA body at rest breaks up into `3` parts. If `2` parts having equal masses fly off perpendicularly each after with a velocity of `12 m//s` when the velocity of the third part which has `3 times` mass of each part is
View SolutionAn explosion blows a rock into three parts. Two parts go off at right angles to each other . These two are `1 kg` first part moving with a velocity of `12 ms^(-1) and 2 kg` second part moving with a velocity of `8 ms^(-1)`. If the third part flies off with a velocity of `4 ms^(-1)`. Its mass would be
View SolutionAn object , initially at rest , explodes in three fragments. The momentum of two pieces are `- 3 p hat(i)` and `-4 p hat(j)` where `p` is a positive number. The momentum of the third piece
(i) will have magnitude `5p`
(ii) will make an angle `tan^(-1) (4//3)` with the `x`-axis
(iii) will make an angle `tan^(-1) (3//4)` with the `x`-axis
(iv) will have magnitude `7 p`
View SolutionA shell is fired from a cannon with a velocity `20 m//s` at an angle `60^(@)` with the horizontal. At the highest point it explodes into three pieces of equal masses . One of the pieces retraces its path to the cannon , the second piece moves vertically up with speed `40 m//s` , the third piece will move with velocity (immediately after the explosion)
View SolutionWhen an expolsive shell travelling in a parabolic path under the effect of gravity explodes in the mid air, the centre of mass of the fragments will move.
View SolutionA body falling vertically downwards under gravity breaks in two parts of unequal masses. The centre of mass of the two parts taken together shifts horizontally towards
View SolutionA bomb of mass `4 m`, while moving on a parabolic path, explodes at highest point of its path. If breaks into two parts of mass ratio `1 : 3`, smaller part coming to rest. The range of this projectile was `60 m` in the absence of explosion. The distance of the second part from the point of projection when it strikes the ground is
View SolutionIn the previous problem , if a bomb explodes into three parts of mass ratio `1 : 1 : 2` , one smaller part retraces its path, the second smaller part coming to rest, the distance from the point of projection , where the heavier part strikes the ground is
View SolutionA ball is released from height `80 m`. When the ball is at height `60 m`, it explodes in two parts of mass ratio `1 : 2`. One of them moves horizontally with speed `20 m//s`. The distance between the two pecies on the ground is
View SolutionA cannon shell is fired to hit a target at a horizontal distance `d`. However , it breaks into two parts of mass ratio `1 : 2` at its height point. The smaller part returns to cannon. The other part
(i) will fall at a distance `d//2` beyond the target
(ii) have eight times the kinetic energy of smaller part
(iii) the increase in kinetic energy of system after explosion is `200 %`
(iv) after explosion , heavier part will take more time as compared to smaller part , to strike the ground
View SolutionA man is standing at the center of frictionless pond of ice. How can he get himself to the shore ?
View SolutionA bullet is fired fram a riffie . If the rifle recoils freely determine whether the kinetic energy of the rifle is greater then , equal or less then that of the bullet .
View SolutionTwo particles having position vectors `vec(r )_(1) = ( 3 hat(i) + 5 hat(j)) meters` and `vec( r)_(2) = (- 5 hat(i) - 3 hat(j)) metres` are moving with velocities `vec(v)_(1) = ( 4 hat(i) + 3 hat(j)) m//s` and `vec(v)_(2) = (alpha hat(i) + 7 hat(j)) m//s`. If they collide after `2 s`, the value of `alpha` is
View Solutionwhich a `U^(238)` nucleus original at rest , decay by emitting an alpha particle having a speed `u` , the recoil speed of the residual nucleus is
View SolutionIn a head on elastic collision of two bodies of equal masses
View SolutionWhich of the following statements is correct ?
(i) In the elastic collsions , the final `K.E.` is equal to the initial `k.E.`
(ii) In an inelastic collision , the final `K.E.` may be smaller or greater than the initial `K.E`.
(iii) In every collision ,momentum is conserved.
(iv) In completely inelastic collision , colliding particles stick to each other and move with same velocity. There will be loss of `K.E.`
View SolutionA particle `P` moving with speed `v` undergoes a head - on elastic collision with another particle `Q` of identical mass but at rest. After the collision
View SolutionA body of mass `m_(1)` moving with a velocity `3 m//s` collides with another body at rest of `m_(2)` . After collision the velocities of the two bodies are `2 m//s` and `5 m//s` , respectively , along the direction of motion of `m_(1)`. The ratio `m_(1)//m_(2)` is
View SolutionA body of mass `2 kg` makes an elastic head - on collision another body at rest and continues to move in the original direction with one fourth of its original speed . The mass of the second body which collides with the first body is
View SolutionTwo equal masses `m_1` and `m_2` moving along the same straight line with velocites `+3 m//s` and `- 5 m//s` respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionA steel ball of radius `2 cm` is at rest on a frictionless surface. Another ball of radius `4 cm` moving at a velocity of `81 cm//see` collides elast cally with first ball. After collision the smaller ball moves with speed of
View SolutionA neutron collides head-on and elasticity with an atom of mass number `A`, which is initially at rest. The fraction of kinetic energy retained by neutron is
View SolutionA neutron makes a head-on elastic collision with a stationary deuteron. The fraction energy loss of the neutron in the collision is
View SolutionA ball of mass `m_(1)` makes an elastic , one-dimensional collision with a stationary particle of mass `m_(2)`. The fraction of the kinetic energy of `m_(1)` transferred to `m_(2)` is
View SolutionIn the previous problem
View SolutionA body of mass `M` moves with velocity `v` and collides elasticity with another body of mass `m(M gt gt m)` at rest , then the velocity of the body of mass `m` is
View SolutionA particle of mass `m` moving with horizontal speed `6 m//s` as shown in the figure. If `m lt lt M` then for one - dimensional elastic collision , the speed of lighter particle after collision will be

View SolutionIn a smooth circular tube of radius `R` , a particle of mass `m` moving with speed `V_(0)` hits another particle of mass `3 m` at rest as shown. The time after which the next collision takes place (assume elastic collision)

View SolutionA point mass of 1kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1kg mass reverses its direction and moves with a speed of `2ms^-1`. Which of the following statements (s) is (are) correct for the system of these two masses?
View SolutionThe ball `A` is reached and it makes head on collision with `B`. The masses of `A` and `B` are same
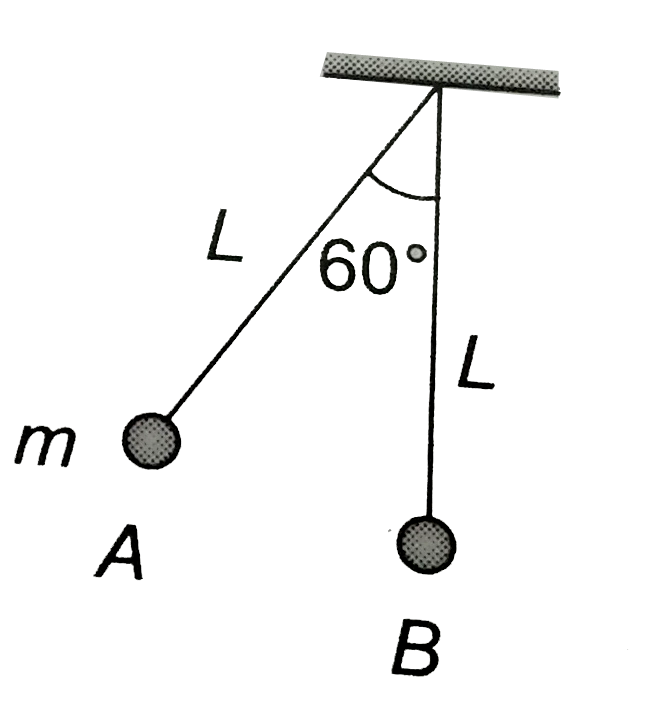
View SolutionA ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, travelling with a velocity `V m//s` in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is

View SolutionThe ball is released when the string is horizontal. The collision between the ball and the block is head - on elastic. The velocities of the ball and the block immediately after collision

View SolutionIn the previous problem , the maximum height attained by the ball and the distance traveled by the block , after collision will be
View SolutionTwo sphere `A and B` of masses `m_(1) and m_(2)` respectivelly colides. A is at rest initally and `B` is moving with velocity `v` along x-axis. After collision `B` has a velocity `(v)/(2)` in a direction perpendicular to the original direction. The mass `A` moves after collision in the direction.
View SolutionA ball , moving with a speed of `10 sqrt(3) m//s` , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of `30^(@)`with the original line of motion. The speeds of two balla after the collision are , respectively.
View SolutionA ball `A` of mass `1 kg` , moving with a speed of `12 m//s` , collides obliquely and elasticity with another ball `B` which was initially at rest. Ball `A` then moves off at the right angle to its initial direction with a speed of `5 m//s`. The momentum of ball `B` after the collision is
View SolutionIn elastic collision between spheres `P` and `Q` of equal mass but unequal radii , move along a straight line. Which of the following may be correct after the collisions ? (i) `P` comes to rest and `Q` moves with velocity of `P`.
(ii) `P` and `Q` move with equal speeds making an angle of `45^(@)` each with original line of motion.
(iii) `P` and `Q` move with unequal speeds , making angles of `30^(@)` and `60^(@)` with the original line of motion , respectively.
(iv) `P` comes to rest:
View SolutionA sphere has a elastic obique collision with another identical sphere which is initially at rest. The angle between their velocities after the collision is
View SolutionTwo small particles of equal masses stant moving in opposite direction from a point `A` in a burtizonetal circule orbic their tangention velocity are `V` and `2V` , respectively as shown in the figure between collsions , the particals move with constant speed After making how many elastic collition , other the then that at `A` these two partical will again reach the point `A` ?

View SolutionWhich of the following is not a perfectly inelastic collision ?
View SolutionA neutron having a mass of `1.67 xx 10^(-27) kg` and moving at `10^(8) m//s`collides with a deuteron at rest and sticks to it. If the mass of the deuteron is `3.33 xx 10^(-27) kg` then the speed of the combination is
View SolutionA body of mass `4 kg` moving with velocity `12 m//s` collides with another body of mass `6 kg` at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
View SolutionA bullet of mass `m` moving with velocity `v` strikes a block of mass `M` at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA shere of mass `m` , moving with velocity `V`, enters a hanging bag of sand and stop. If the mass of the bag is `M` and it is reised by height `h`, then the velocity of the sphere will be
View SolutionA particle of mass `m` moving eastward with a speed `v` collides with another particle of the same mass moving coalesce on collision. The new particle of mass `2 m` will move in the north - easterly direction with a velocity
View SolutionA mass 'm' moves with a velocity 'v' and collides inelastieally with another identical mass . After collision the `1^(st)` mass moves with velocity `v/sqrt3` in a direction perpendicular to the initial direction of motion. Find the speed of the `2^(nd)` mass after collision.
`undersetunderset ((before),(collision))(m)(*rarr) underset(m)* uparrow v//sqrt3 underset((after),(collision):)`
View SolutionA bullet of mass `10 g` moving horizontally with a speed of `400 m//s` a block of mass `390 g` and remains in it. The block slides `10 m` on rough surface before coming to rest. The friction coefficient is
View SolutionIn the previous problem , the bullet penetrates the block and emerges with speed `v_(0)`.If the block travels `2.5 m` on the rough surface , the value of `v_(0)` is
View SolutionA bullet of mass `20 g` moving horizontally strikes a block of mass `480 g` suspended by a string of length `2 m`. If the collision is completely inelastic , the minimum velocity of bullet , so that the combined mass complete vertical circle should be
View SolutionIn the previous problem. If the bullet is moving with velocity `50 sqrt(2) m//s`, the maximum angle made by string with vertical is
View SolutionConsider the situation as shown in the diagram. The bullet penetrates the block and emerges with speed `v_(0)//3`. If after collision , the string becomes horizontal , `v_(0)` will be

View SolutionA block of mass `2m` is attached to a string of length `L = 5 m`. The block is released when the string is horizontal , it picks up a particle of `2 m` kept at rest at the lowest point. The maximum height attached by the combined mass is
View SolutionIn the previous problem , if the horizontal surface is rough with friction coefficient `0.5` and collision is elastic , head - on , the distance travelled by the block on the rough surface
View SolutionThree objects `A` ,` B` and `C` are kept in a straight line on a smooth horizontal surface. These have masses `m `, `2m` and `3 m` , respectively . The head - on elastic collision takes place between `A` and `B` and then `B` makes completely inelastic collision with `C`. All motions occur on the same straight line. The final speed of `C` will be
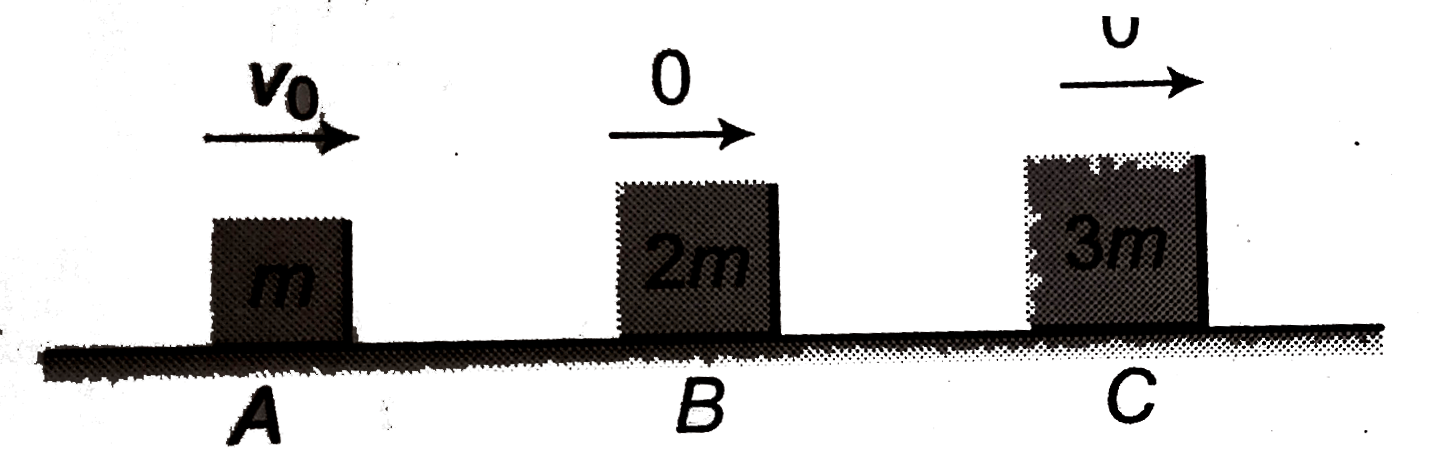
View SolutionA set of a identical cubical blocks lies at rest parallel to each other along a line on a smooth horizontal surface. The separation between the near surface of any two adjacent blocks is `L`. The block at one and is given a speed `v` towards the next one at time `t = 0`. All collision are completely inelastic , then the last block starts moving at
View SolutionA ball moving with velocity `2 ms^(-1)` collides head on with another stationary ball of double the mass. If the coefficient of restitution is `0.5`, then their velocities (in `ms^(-1)`) after collision will be
View SolutionA sphere `A` impinges directly on an identical sphere `B` at rest. If coefficient of restitution is `e` , the ratio of velocities of `A` and `B` after collision is
View SolutionIn the previous problem , sphere `A` is moving with speed `u_(1)` and sphere `B` with speed `u_(2)` in opposite direction. After the collision , sphere `A` comes to rest , then `u_(1)//u_(2)` is
View Solution
Exercises questions and complete solutions for chapter CENTER OF MASS of CP SINGH PHYSICS (HINGLISH) of Class 11