Complete Solutions to Example of chapter CENTER OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTER OF MASS |
| CP SINGH | Example |
| Number Of Questions | 79 |
| Academic Year | 2023-24 |
The four particles of masses ` m , 3m, 2m` and `4m` are placed on the vertices of a sqare of side `L`. Locate the center of mass
 03:33View Solution
03:33View SolutionConsider the situation as shown in the figure. Locate the center of mass.
 03:44View Solution
03:44View SolutionLocate the center of mass.
 04:14View Solution
04:14View SolutionTwo identical rods each of mass `m` and length are connected as shown. Locate `c.m.`
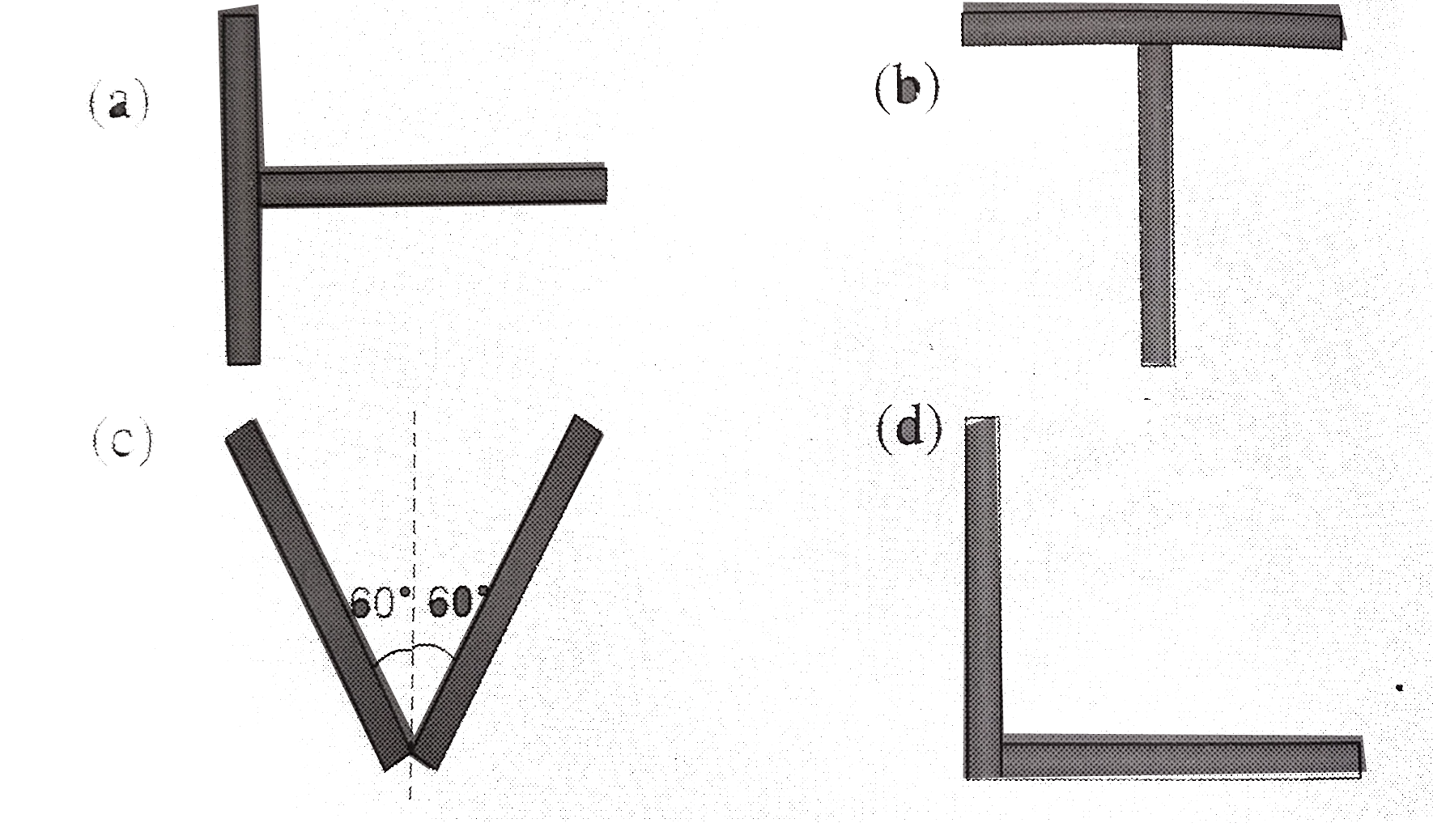 10:01View Solution
10:01View SolutionThree thin uniform rods made of same material are joined as shown. Locate x coordinate of COM.
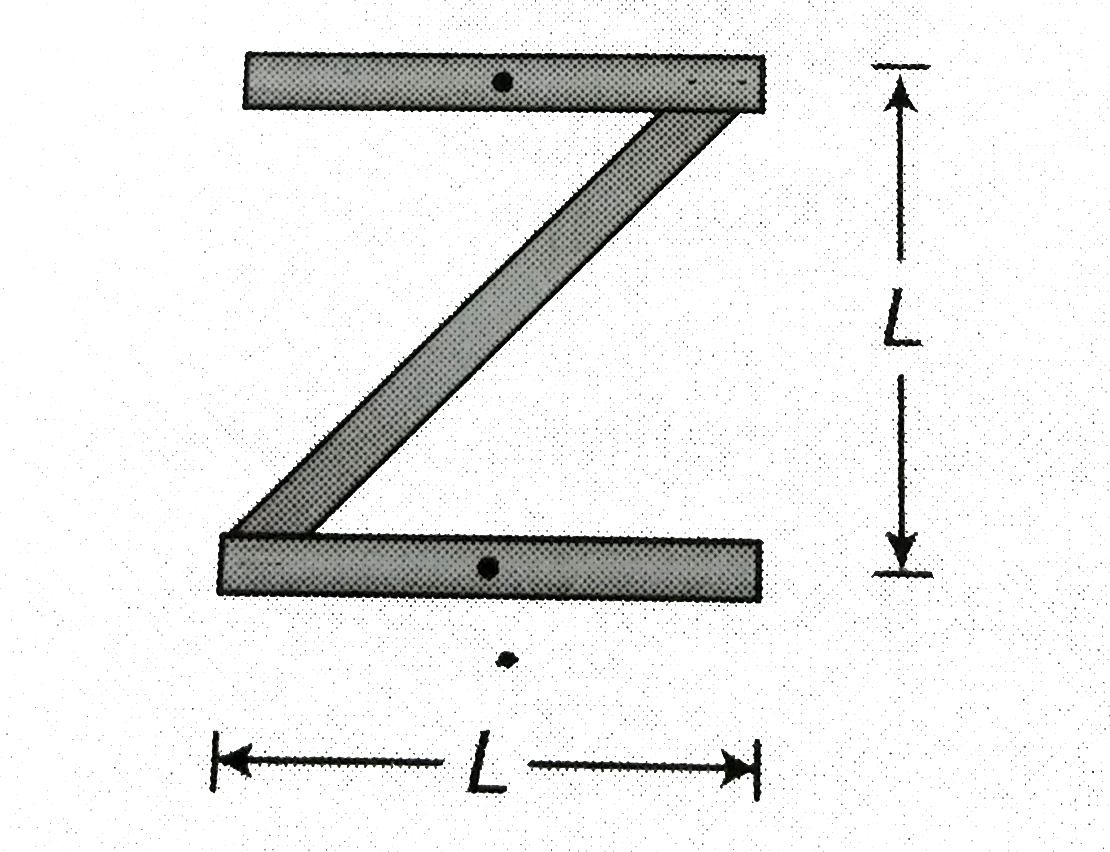 06:40View Solution
06:40View SolutionTwo uniform discs made of same material and thickness of redii `R` and `2 R` are joined as shown. Locate `c.m.`
 04:46View Solution
04:46View SolutionTwo plates made of the same material and thickness are joined as shown. One plate is circular and another square in shape. The diameter of circular plate is equal to the side of the square plane. Locate `c.m.`
 06:32View Solution
06:32View SolutionFrom a circular disc of radius `R`, another disc of diameter `R` is removed. Locate `c.m.` of the remaining portion.
 04:53View Solution
04:53View SolutionFrom a semicircular disc of radius `r_(1)`, another semicircular disc of radius `r_(2)` is removed. Find the `c.m.` of the remaining position.
 04:54View Solution
04:54View SolutionA right circular cone of radius `R` and height `2 R` is placed on a hemisphere of radius `R`. Locate `c.m.` of the combined mass from `O`.
 04:02View Solution
04:02View SolutionThe linear mass density i.e. mass per unit length of a rod of length `L` is given by `rho = rho_(0)(1 + (x)/(L))`, where `rho_(0)` is constant , `x` distance from the left end. Find the total mass of rod and locate `c.m.` from the left end.
 04:46View Solution
04:46View SolutionLocate `c.m.` of thin , uniform semicircular wire of radius `R`.
04:56View SolutionLocate `c.m.` of thin , uniform semicircular plate.
04:55View SolutionThe three particles of mass `m , 2m` and `3m` are located at `(1 , 2, 3) , ( 2, 3, 4)` and `(1, 1,1)`. Find the position vector of `c.m.`
03:45View SolutionA system consists of three particles in motion as shown. Find the velocity of `c.m.`
 01:59View Solution
01:59View SolutionFind the velocity of `c.m.`
 03:07View Solution
03:07View SolutionTwo particles of masses `2m` and `3m` are placed at separation `d` on a smooth surface. They move towards each other due to mutual attractive force. Find (a) acceleration of c.m. (b) Velocity of c.m. when separation between particles becomes `d//3`. ( c) At what distance from the initial position of mass `2m`, the particles collide.
03:55View SolutionA `20 kg` kid is sitting in a `60 kg` boat in a lake. The distance of kid from the bank of lake is `20 m`. If the kid moves `8m` on the boat towards the bank, then find the distance of kid from the bank. The system is initially at rest and there is no friction between boat and water.
04:02View SolutionA boy of mass `40 kg` is standing at one ned of the boat (mass : 80 kg) of length 6m in a river. Now the boy reaches to other end of the boat. Find the distance moved by the boat and the distance travelled by boy as seen from the bank of river.Assume that the system is at rest and no friction between the boat and the water.
04:56View SolutionAll surfaces are smooth. The ball of mass `m` is released from `A`. Find the distance travelled by the block of mass `M`.
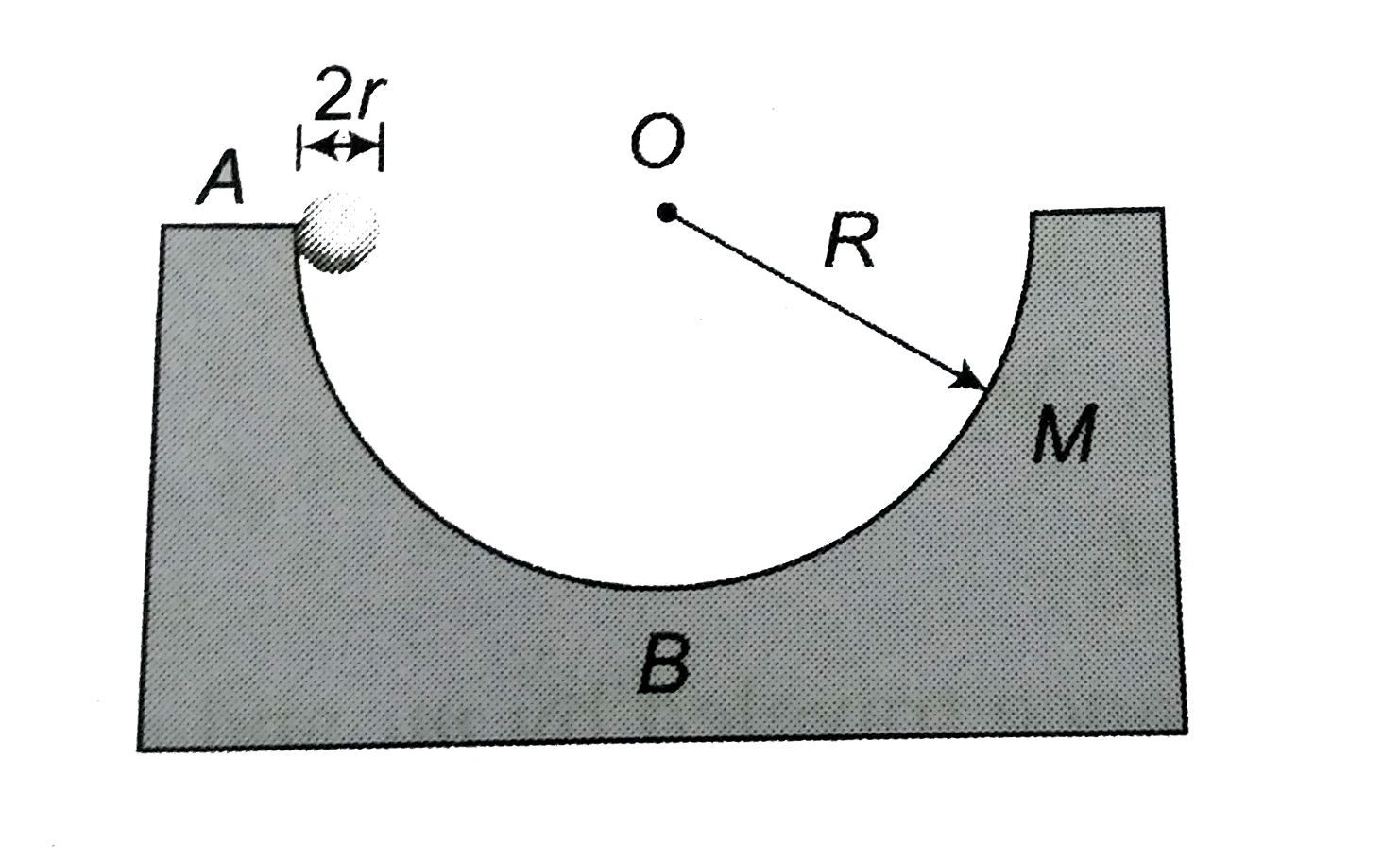 04:28View Solution
04:28View SolutionA small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
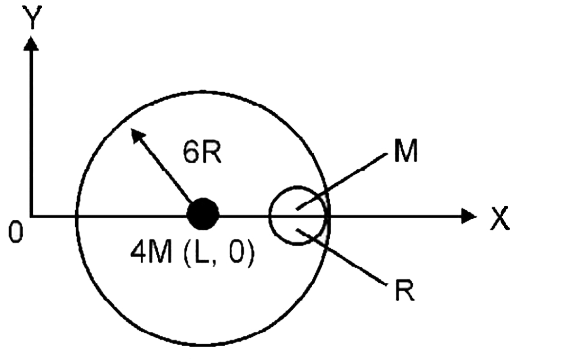 04:38View Solution
04:38View SolutionA bomb is thrown at a speed `20 m//s` at an angle `45^(@)`. At the highest point , it explodes into two parts of equal mass , the one part coming to rest. Find the distance from the origin to the point where the other part strikes the ground.
03:59View SolutionA bullet of mass `50 kg` is fired with a speed of `200 m//s` from a gun of mass `2 kg` . Find the recoil velocity of the gun.
02:22View SolutionA bomb of mass `4 m` explodes into two parts of mass ratio `1 : 3`. If the `K.E`. Of smaller fragment is `K` , find the `K.E.` of the larger fragment.
04:04View SolutionA shell is fired from a cannon with a velocity `v (m//sec.)` at an angle `theta` with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon and the speed (in `m//sec.`) of the other piece immediately after the explosion is
03:48View SolutionAs shown , a small body of mass `50 g` placed over a larger mass `1950 g` whosw surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed `20 m//s` and the system is left to itself. All surfaces are smooth. Find the speed of the larger block when the smaller block is moving on the vertical part.
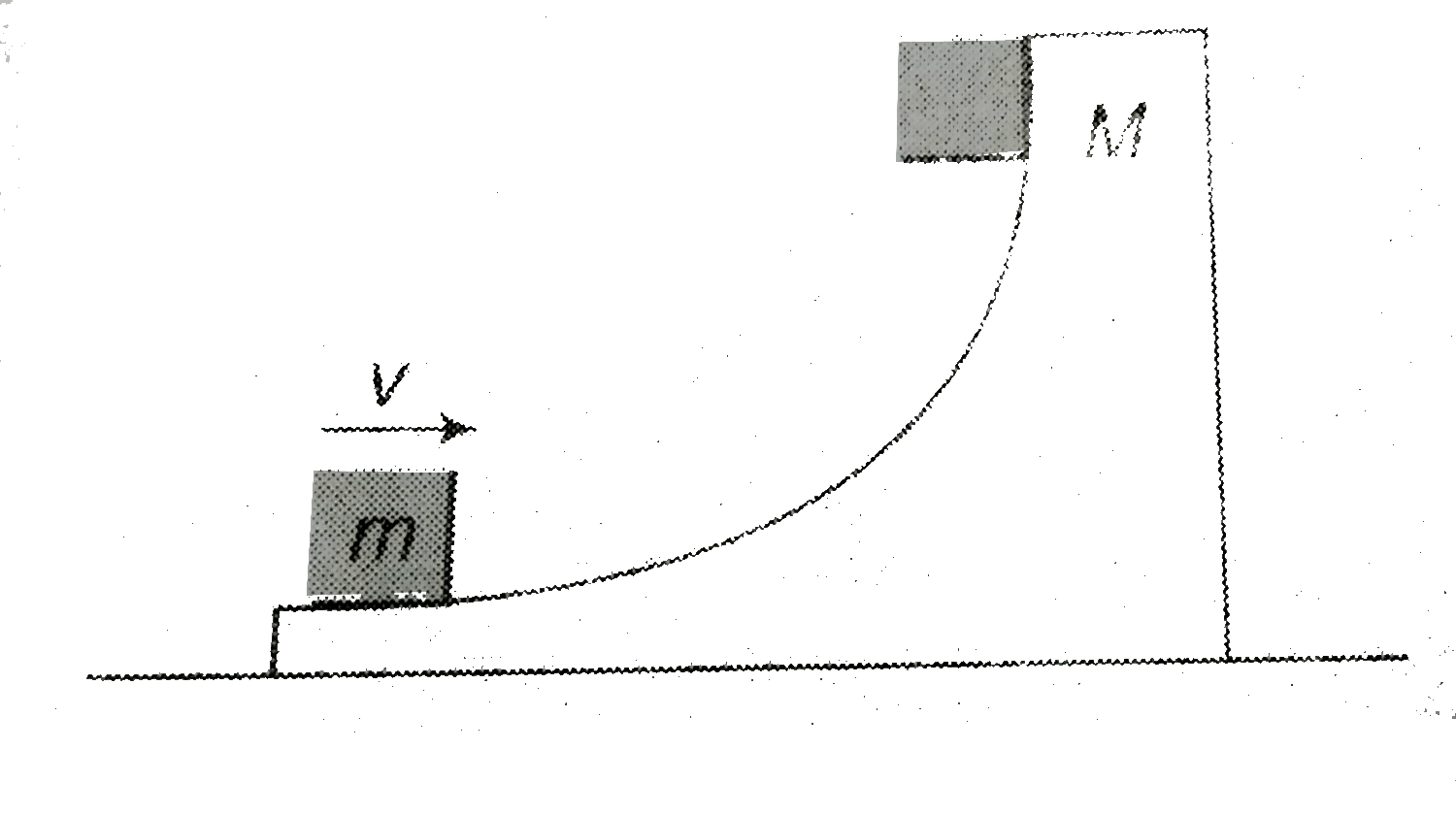 03:03View Solution
03:03View SolutionA `U^(238)` nucleus , initially at rests , emits an alpha particle with a speed `v_(0)`. Calculate the recoil speed of the residual nucleus `Th^(234)`. Assume that the mass of a nucleus is proportional to the mass number. Also , calculate the ratio of `K.E. of Th^(234)` and `alpha` -particle.
03:27View SolutionA bomb of mass `5 m` initially at rest explodes and breaks into three pieces of masses in the ratio `1 : 1 : 3`. The two pieces of equal mass fly off perpendicular to each other with a speed of `v_(0)`. What is the velocity of the heavier piece? Also , calculate the energy released in explosion.
04:17View SolutionThree particles A, B and C of equal mass move with equal speed V along the medians of an equilateral triangle as shown in hgure. They collide at the centroid G of the triangle. After the collision, A comes to test, B retraces its path with the speed V. What is the velocity of C ?
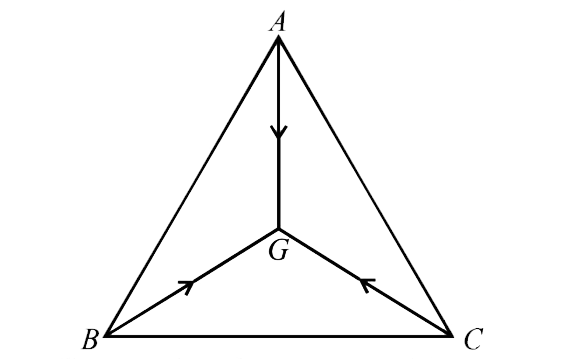 02:24View Solution
02:24View SolutionA boy of mass `m` is standing on a platform of `M` kept on smooth floor. If the body starts moving on the platform with a speed `v_(0)` relative to the platform , with what velocity to the floor does the platform recoil ?
02:26View SolutionA cannon of mass `m_(1)` fires a shell of mass `m_(2)` with speed `v_(0)` relative to the barrel which is inclined at an angle `alpha` with horizontal . Find the recoil speed of cannon if it is placed on ice.
03:29View SolutionA block at rest is suddenly burst into two pieces of mass `2 kg` and `4 kg` , respectively . The pieces fly apart with a relative of `30 m//s`, determine the speed of each. If the coefficient of friction for surface is `0.5` , find the separation between pieces when they come at rest.
07:08View SolutionA boy of mass `m` is riding on a trolley of mass `M` which is moving on smooth floor at speed `v_(0)`. He jumps off in the opposite direction of motion of trolley with velocity `u` relative to the trolley before the jump. Find the velocity of the trolley after jump.
04:38View SolutionTwo boys each of mass `40 kg` are standing on the right side of a trolley of mass `80 kg` , initially at rest on smooth floor. The boys jumps to the right with velocity `3 m//s` with respect to the trolley before the jump. Find the final velocity of the trolley if the jumps : (a) together , (b) one after the other and (c ) one boy is on the left and the other on the right , the boy on the left jumps to the left and then the boy on the right jumps to the right. Each boy jumps with `3 m//s` with respect to the trolley before the jump.
06:25View SolutionA boy of mass `40 kg` moves on a `10 m` long , `60 kg` railroad car on the smooth horizontal floor. Now the boy moves with speed `5 m//s`. (a) Find the velocity of the car with respect to the floor. (b) If the boy starts from middle of the car and reaches to one end of the car , find the distance traveled by the car. (c ) If the boy stops at the end , find the velocity of the car. (d) If the boy falls off the car at one end while walking , find the velocity of the car.
04:52View SolutionTwo identical buggies 1 and 2 with one man in each move without friction due to inertia along the parallel rails toward each other. When the buggies get opposite each other, the men exchange their places by jumping in the direction perpendicular to the motion direction. As a consequence, buggy 1 stops and buggy 2 keeps moving in the same direction, with its velocity becoming equal to v. Find the initial velocities of the buggies `v_1` and `v_2` if the mass of each buggy (without a man) equals M and the mass of each man m.
04:29View SolutionA block of mass `M` with a semi - circular track of radius `R` rests on a smooth floor. A sphere of mass `m` and radius `r` is released from rest from `A`. Find the velocity of sphere and track , when the sphere reaches `B`.
 09:52View Solution
09:52View SolutionA small block of super dense material has a mass equal to the half of the mass of the earth . It is released from the height `H(H lt lt ` radius of the earth) . Find its speed when its height from the eath surface decreases by `75%`.
06:28View SolutionA block of mass `m` is placed on a triangular block of mass `M(M = 2m)` , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.
 07:16View Solution
07:16View SolutionA block of mass `(M = 2m)` is placed on smooth surface. Another block of mass `m` is given velocity `sqrt(9 gh)` in horizontal direction , as shown. Find the speed of `m` when it breaks off from `M`. Also , calculate the maximum height attained by it from its initial level. Take `h = 2m`.
 09:21View Solution
09:21View SolutionA particle of mass `m` moving on a smooth surface with velocity `10 m//s` strikes another particle of mass `2 m` moving with `5 m//s` in the same direction . If the collision is elastic and head - on , find velocities of particles after the collision.
04:21View SolutionSolve the previous problem , if particles moving in opposite direction.
03:47View SolutionA particle of mass `m_(1)` moving on a smooth surface with some velocity strikes another particle of mass `m_(2)` at rest. The head - on elastic collision takes place. After the collision , particles move with equal speed in opposite direction . Determine the mass ratio.
03:39View SolutionA particle of mass `m` moving with some velocity on a smooth surface strikes another particle of mass `eta m` at rest , elasticity head - on. What fraction of incident `K.E.` is transferred to the particle of mass `eta m`.
05:48View SolutionIn the previous problem , find the value of `eta` if the the particle of mass `eta m` should recoil with (a) the greater `K.E.` . (b) the greatest momentum and ( c) the greatest speed.
05:28View SolutionA bullet of mass `m` moving with velocity `u` on smooth surface strikes a block of mass `M` kept at rest. The collision is completely inelastic. Find the common velocity and the fractional loss in kinetic energy.
04:17View SolutionIn the previous problem , the block of `mass M` is attached to a string of length `L`. Find the maximum angle made by the string with vertical . Take veloctiy of buller `u = 4 sqrt(g L)`. Take `M = 3m`.
04:41View SolutionA bullet of mass `10 kg` moving horizontally at a speed `140 m//s` strikes a block of mass `100 g` attached to a string like a simple pendulum. The bullet penetrates the block and emerges on the other side. If the block rises by `80 cm` , find final velocity of bullet.
04:43View SolutionA ball `A` of mass `m` attached to a string of length `L` is released when the string is horizontal. It strikes another ball `B` of mass `2 m` suspended to another string of length `L` at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
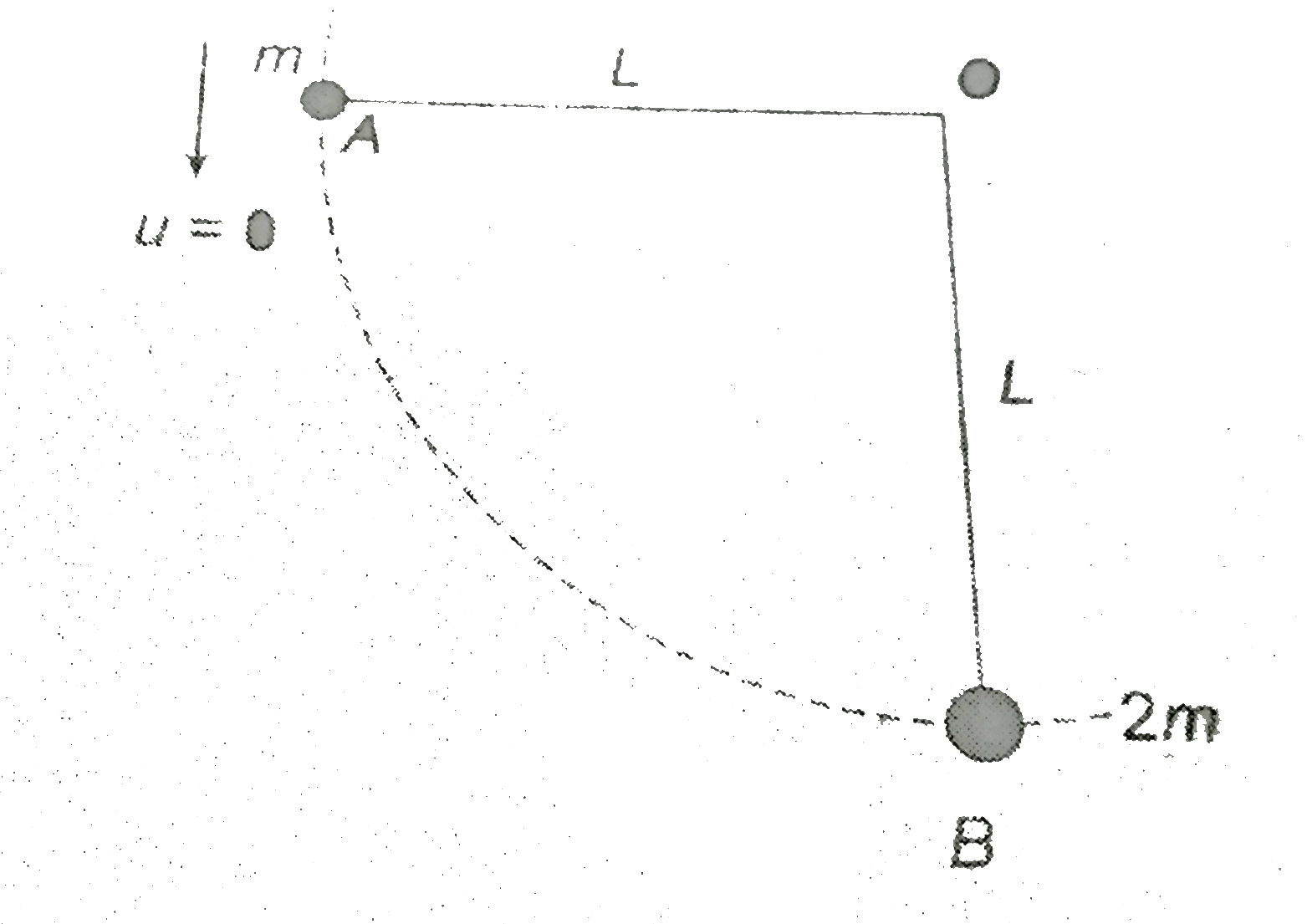 06:07View Solution
06:07View SolutionIn the previous problem , if the collision is head - on elastic , find (a) the velocities of balls immediately after the collision and (b) the maximum height attained by eacl ball.
06:13View SolutionThe ball `A` of mass `m` is released when the string is horizontal. It strikes a block `B` of mass `3 m` kept on a rough surface of friction coefficient `mu = 0.1`. If a head on elastic collision takes place , find the maximum distance travelled by the block on a rough surface.
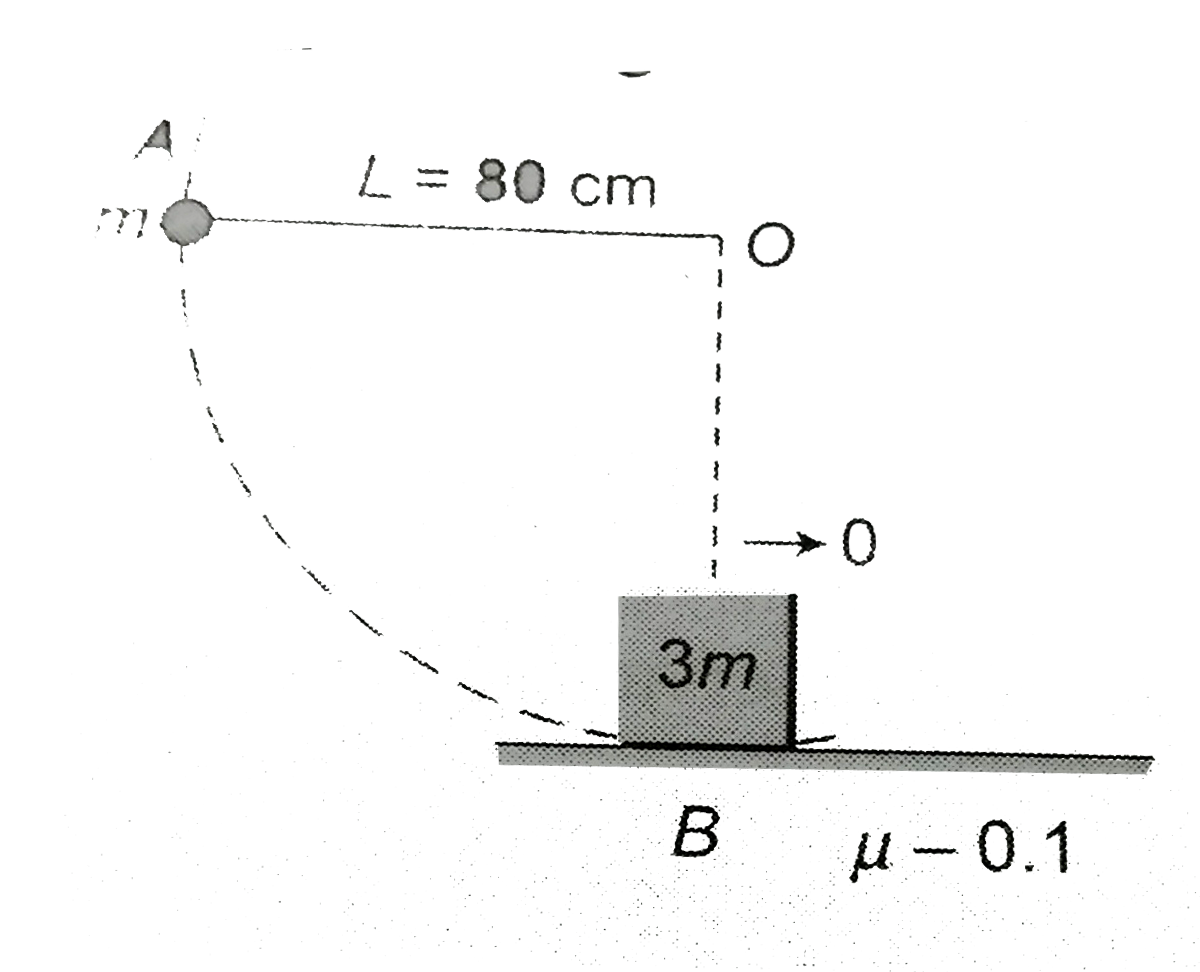 05:34View Solution
05:34View SolutionIn the previous problem another block `C` of mass `m` is placed at distance `1 m` right of block `B`. Find `(a)` the distance travelled by the combined mass if the collision is completely inelastic and `(b)` separation between the blocks when they stop after head - on elastic collision.
09:25View SolutionTwo blocks `A` and `B` of masses `m` and `2m` are connected by a massless spring of natural length `L` and spring constant `k`. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block `C` of mass `m` moves on the floor with a speed `v_(0)` along the line joining `A` and `B` and collides elastically with `A`. FInd `(a)` the velocity of `c.m.` of system `(block A + B + spri ng)` and `(b)` the minimum compression of spring.
 08:22View Solution
08:22View SolutionBlock of mass `2 m` is given `v_(0)` towards the right. If `L` is the natural length of spring constant `k`, find the maximum elongation of the spring.
 04:39View Solution
04:39View SolutionThe ball strikes the block and sticks to it. Find the maximum compression of spring. (`L`: natural length of spring)
 03:42View Solution
03:42View SolutionA block of mass `180 g` is placed on a spring (spring constant `k = 120 N//m`) fixed from below. A ball of mass `20 g` is dropped from height `20 m` and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
10:30View SolutionA block of mass `180 g` is suspended by a massless spring. The spring extends by `1.8 cm` due to the weight of block. A particle of mass `20 g` is dropped from a height `80 cm` on the block. The collision is completely inelastic . Find the maximum elongation of the spring.
06:59View SolutionTwo blocks of masses `m` and `2m` compress a spring of spring constant k by `x_(0)` and blocks are a connected by a thread and placed on a smooth surface as shown. Now , thread is burned. Find the speed of each block when the spring attains its normal length `L`.
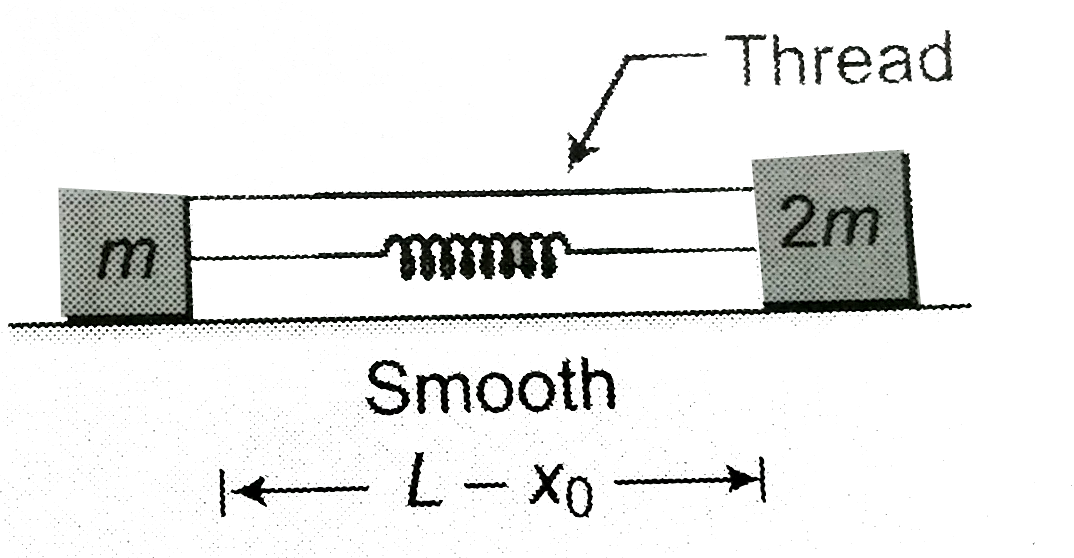 04:19View Solution
04:19View SolutionA ball of mass `m` moving with speed `v` towards the right strikes a wall moving towards the left with speed `u`. Find the change in the `K.E.` of the ball if the collision is elastic.
04:29View SolutionA ball of mass `m` moving with velocity `u` strikes another identical ball at rest. Find the velocities of the balls after the collision if the coefficient of restitution is `e` and the collision is head -on. Also , calculate the loss in `K.E.`
06:08View SolutionIf in the previous problem , the final `K.E.` is `3//5` of the initial `K.E.` , find the value of `e`.
03:10View SolutionA ball strikes directly upon another ball at rest and is itself reduced to rest by the impact. If half of the initial `K.E.` is lost in collision, find the value of `e`.
05:12View SolutionA particle of mass `m` experienced an elastic collision with a stationary particle of mass `2m` . What fraction of the kinetic energy does the striking particle lose if recoils at the right angles to its original motion direction.
View SolutionParticle `1` experiences a perfectly elastic collision with a stationary particle `2`. Determine their mass ratio , if the particles fly symmetrically relative to the initial motion direction particle `1` with angle of divergence `theta = 60^(@)`.
06:18View SolutionParticle `1` experiences a perfectly collision with a staionary particle `2`. Determine their mass ratio , if the particles move perpendicularly to each other.
04:16View SolutionA particle of mass `m` strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
04:39View SolutionA particle of mass `m` moving with velocity `v_(0)` collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.
 View Solution
View SolutionA soccer ball of mass `500 g` is moving horizontally to the left with speed `14 m//s`. The ball is kicked and given velocity `30 m//s` at angle `53^(@)` with horizontal in upward direction to the right. Find the impulse of net force and average net force, assuming the collision time `0.01 s`.
`(cos 53^(@) = 3//5 , sin 53^(@) = 4//5)`04:23View SolutionA particle of mass `m` strikes a smooth floor with speed `u` at angle of incidence `theta` with the normal. The coefficient of resultant is `e`. Find the magnitude and direction of velocity with which the particle rebounds. Also, find the impulse and loss in `K.E.`
View SolutionA ball is thrown from the ground with velocity `u` at an angle `theta` with horizontal. If the coefficient of restitution is `e` , find the time of flight , the maximum height and the horizontal range after the first collision.
05:11View SolutionA ball is dropped from the height `h` on an inclined plane of inclination `theta`. If the coefficient of restitution is `e`, at what distance along the plane , the ball again collides with the plane.
View SolutionA ball is given velocity `u = sqrt(3 gd)` at an angle `45^(@)` with horizontal. It strikes a wall at distance `d` and returns to its original position. Find the coefficient of restitution `e`.
View SolutionA ball after falling a distance collides an inclined plane of inclination `theta`. If after the collision , the ball moves horizontally , find the coefficient of restitution.
 01:54View Solution
01:54View SolutionA ball is attached to a string of length `L`. The ball is released when the string is horizontal. The ball collides with wall and `e = 2//sqrt(5)`. After how many minimum number of collisions , the amplitude of oscillation becomes less than `60^(@)`.
 View Solution
View SolutionA rocket of initial mass `6000 kg` ejects gases at constant rate of `20 kg//s` with constant relative speed of `8 km//s`. What is the acceleration of the rocket after `100 s`.
(a) Neglect gravity , (b) include gravity and (c ) upward thrust.02:57View SolutionA rocket is set for a vertical firing . If the exhaust speed is `2000 m//s` , find the rate of fuel consumption initial vertical upward acceleration of `30 m//s^(2)`. Take mass of rocket `= 6000 kg`.
04:59View SolutionIn the previous problem , if the mass of fuel is `5000 kg` and the rate of fuel consumption is `50 kg//s` , find the speed acquired by the rocket when all fuel is consumed .
06:29View SolutionA uniform chain of mass M and length L is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to rest. Assuming that the chain does not form a heap on the floor, calculate the force exerted by it on the floor when a length x has reached the floor.
07:44View SolutionA ball is dropped from a height h on a floor if the coefficient of restitution ise. Find the
(a). Speed of ball after the first second … `n^(th)` collision.
(b). Maximum height attained by the ball, after the first, second … `n^(th)` collision.
(c). Time taken by the ball to reach the highest point after the first, second, ...`n^(th)` collision.
(d). total distance covered by the ball.
(e). totol time of journey.View Solution
Example questions and complete solutions for chapter CENTER OF MASS of CP SINGH PHYSICS (HINGLISH) of Class 11
