Complete Solutions to EXAMPLE of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| DC PANDEY NEET | EXAMPLE |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
A gas filled in a cylinder fitted with movable piston is allowed to expand. What is the nature of the work done by the gas?
View SolutionA lawn roller has been pushed by a gardener through a distance of 30 m. What will be the work done by him, if he applies a force of 30 kg-wt in the direction inclined at `60^(@)` to the ground?
View SolutionA rigid body moves a distance of 10m along a straight line under the action of a force 5N. If the work done by this force on the body is 25 joules, the angle which the force makes with the force makes with the direction of motion of the body is:
View SolutionA block of mass `m=2kg ` is pulled by a force `F=40 N` upwards through a height `h=2 m.` Find the work done on the block by the applied force `F` and its weight mg. `(g=10m//s^2)`.

View SolutionA 10 g block placed on a rough horizontal floor is being pulled by a constant force 50 N. Coefficient of kinetic friction between the block and the floor is 0.4. Find work done by each individual force acting on the block over displacement of 5 m.
View SolutionA block of mass 2 kg is being brought down by a string. If the block acquires a speed `1(m)//(s)` in dropping down 25 cm, find the work done by the string in the process.
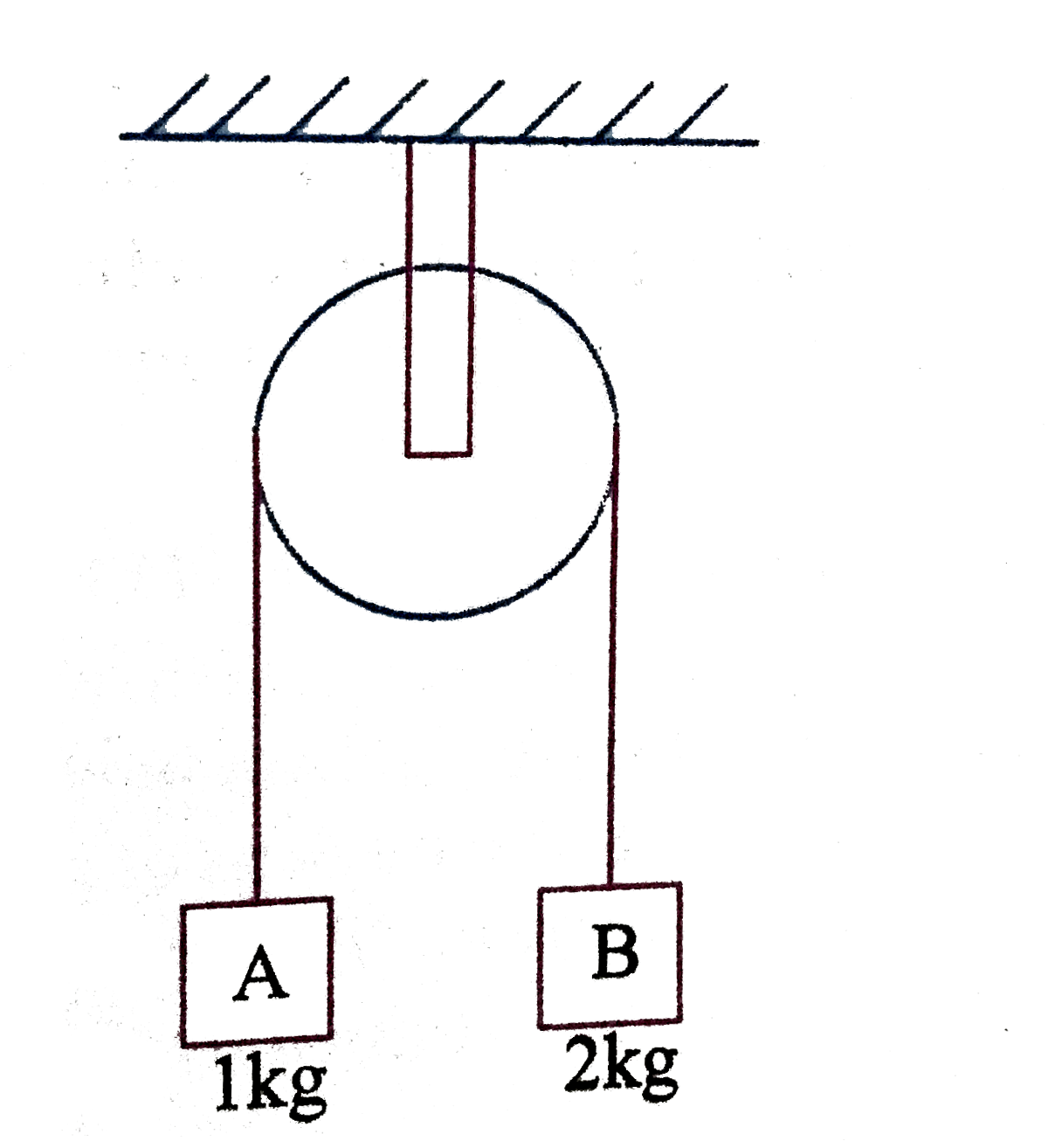
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 `ms^(-2)`)

View SolutionA constant force `F=(hati+3hatj+4hatk)N` acts on a particle and displace it from (-1m,2m,1m)to(2m,-3m,1m).
View SolutionA particle is shifted from point (0,0,1m)to (1m,1m,2m), under simultaneous action of several forces. Two of the forces are `F_(1)=(2hati+3j-k)N " and " F_(2)=(hati-2hatj+2hatk)N`. Find work done by resultant of these two forces.
View SolutionA position dependent force
`F=(7-2x+3x^(2))N`,
acts on a small body of mass 2kg and displaces it from `x=0` to `x=5`m. Work done in joule is
View SolutionA force `F=(2+x)` acts on a particle in x-direction where F is in newton and x in metre. Find the work done by this force during a displacement form 1. 0 m to x = 2.0 m.
View SolutionA force `F=-k/x_2(x!=0)` acts on a particle in x-direction. Find the work done by this force in displacing the particle from. `x = + a` to `x = 2a`. Here, k is a positive constant.
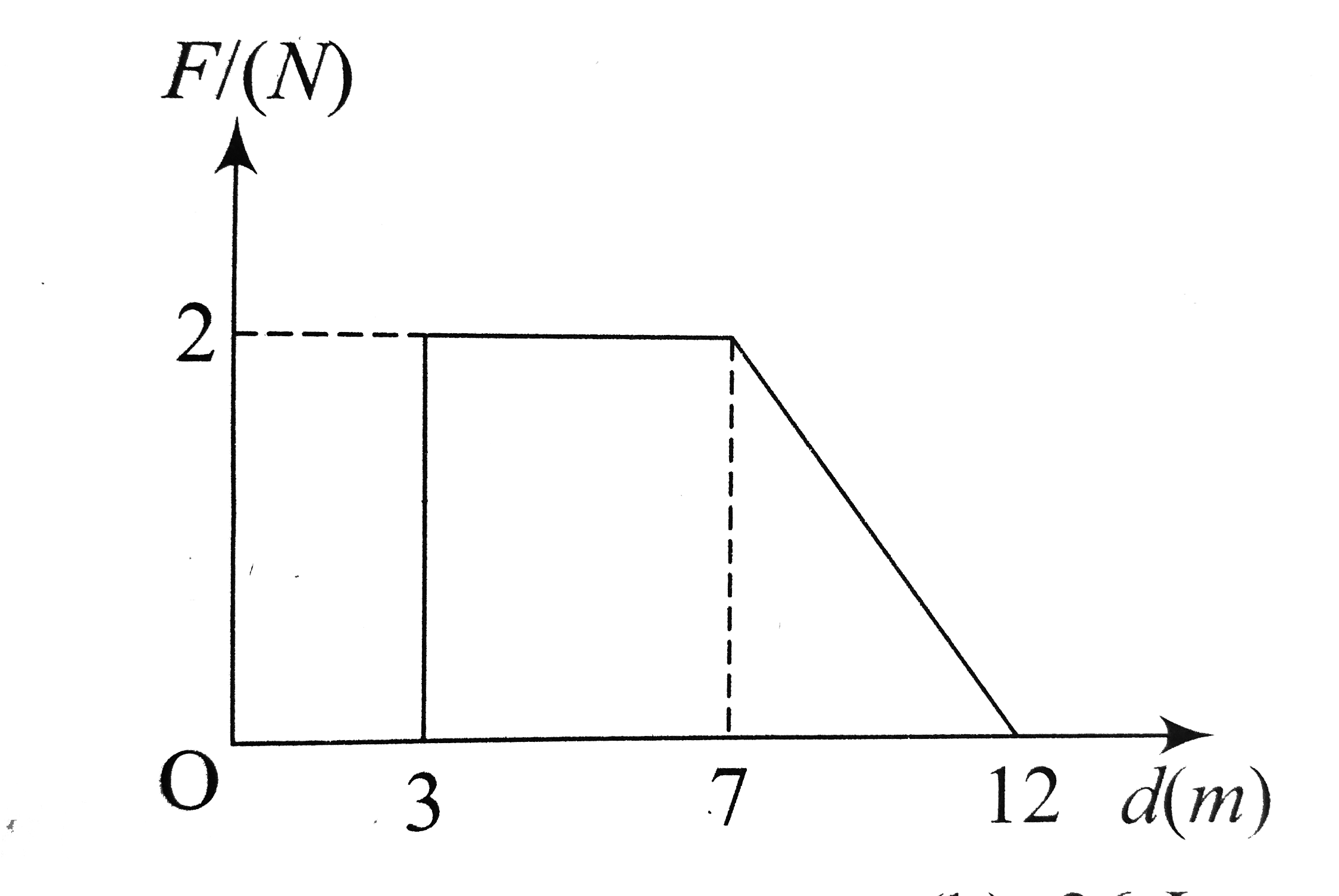
View SolutionForce `F` on a particle moving in a straight line varies with distance `d` as shown in the figure. The work done on the particle during its displacement of `12 m` is
View SolutionThe relationship between force and position is shown in fig ( in one dimensional case). The work done in displacing a body from x=1cm to x = 5 cm is:
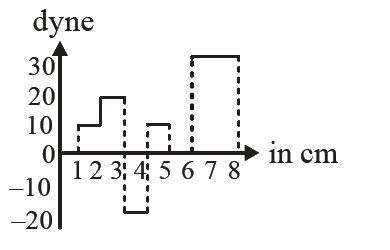
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionThe work done in extending a spring by `x_0` is `W_0`. Find the work done in further extension `x_0`.
View SolutionConsider a block connected to a light spring of spring constant `100Nm^(-1)`. Now the block is displaced by applying a constant force F which gives zero resultant force when spring is stretched through 10 cm.
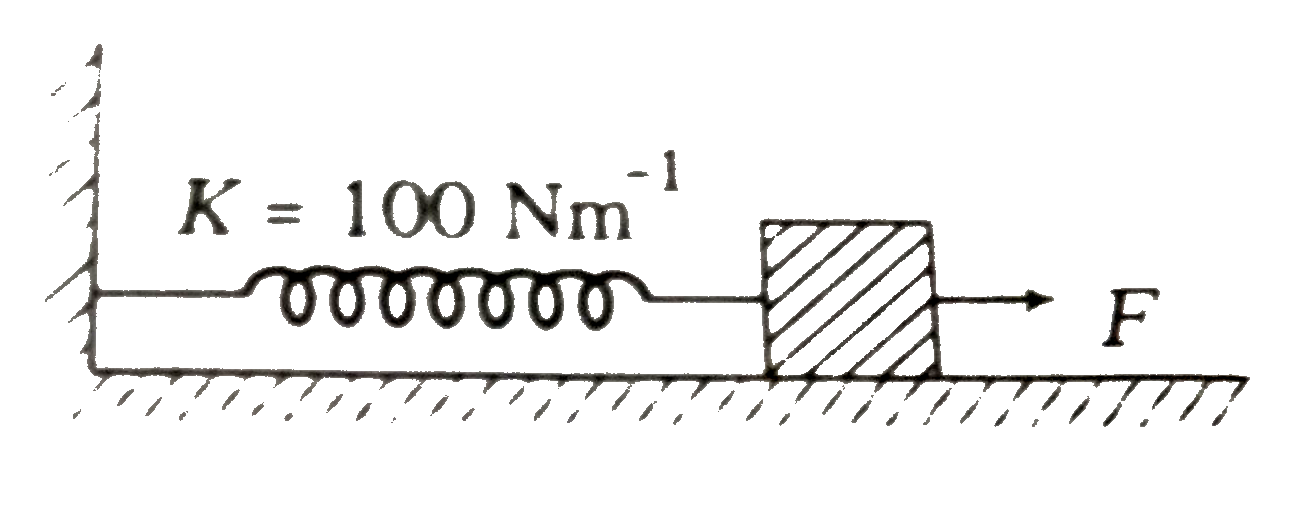
Evaluate
(i) Work done by the spring force when the block attains equilibrium.
(ii) Net work done on the block when it attains maximum speed.
View SolutionA train is moving with a speed of `90 kmh^(-1)` passenger X inside the train displaces his 40 kg, luggage slowly an the floor through 1 m in 10 s. Coefficient of friction of the floor of the train is 0.2. Find the work done by this passenger X and the luggage as seen by
(i) a follow passenger Y
(ii) a person on the ground [Take ,g=10 `ms^(-1)`].
View SolutionAn object is displaced from point A(2m,3m,4m,) to a point B (1m,2m,3m) under a constant force `(2hati+3hatj+4hatk)` N. Find the work done by this force in this process.
View SolutionAn object is displaced from positin vector `r_1=(2hati+3hatj)` m to `r_2=(4hati+6hatj)` m under a forc `F=(3x^2hati+2yhatj)N` Find the work done by this force.
View SolutionA body of mass 0.3 kg is taken up an inclined plane of length 10 m and height 5 m, and then allowed to slide down the bottom again. The coefficient of friction between the body and the plane is 0.15. What is the
(i) work done by the applied force over the upward journey?
(ii) work the by gravitational force over the round trip?
(iii)work the by the frictional force over the round trip?
Which of the above forces (except applied force )is/are conservative forces?
View SolutionIf a man increase his speed by 2m/s, his K.E. is doubled, the original speed of the man is
View SolutionIn a ballistics demonstration, a police officer fires a bullet mass `50.0g` with speed `200ms^(-1)` on soft plywood of thickness 2.00cm. The bullet emerges only with `10%` of its initial kinetic energy. What is the emergent speed of the bullet ?
View SolutionA body of mass 0.8 kg has intial velocity `(3hati-4hatj) ms^(-1)` and final velocity `(-6hatj+2hatk) ms^(-1)`. Find change in kinetic energy of the body?
View SolutionTwo bodies A and B having masses in the ratio of 3 : 1 possess the same kinetic energy. The ratio of their linear momenta is then
View SolutionKinetic energy of a particle is increased by 300 %.Find the percentage increase in momentum.
View SolutionThe position (x) of a particle of mass 1 kg moving along x-axis at time t is given by `(x=(1)/(2)t^(2))` meter. Find the work done by force acting on it in time interval from t=0 to t=3 s.
View SolutionA bullet weighing 10 g is fired with a velocity of `800 ms^(-1)`. After passing through a mud wall 1 m thick, its velocity decreases to `100 ms^(-1)`. Find the average resistance offered by the mud wall.
View SolutionAn object of mass 5 kg falls from rest through a vertical distance of `20 m` and attains a velocity of 10 m/s. How much work is done by the resistance of the air on the object?
`(g=10m//s^(2))`.
View SolutionA particle of mass m moves on a straight line with its velocity varying with the distance travelled according to the equation `v=asqrtx`, where a is a constant. Find the total work done by all the forces during a displacement from `x=0 to x=d`.
View SolutionA block of mass `10 kg` is moving in x-direction with a constant speed of `10 m//s`. it is subjected to a retarding force `F=-0.1 x J//m`. During its travel from `x =20m` to `x =30 m`. Its final kinetic energy will be .
View SolutionAn object of mass `m` is tied to a string of length `l` and a variable force F is applied on it which brings the string gradually at angle thit `theta` with the vertical. Find the work done by the force `F`
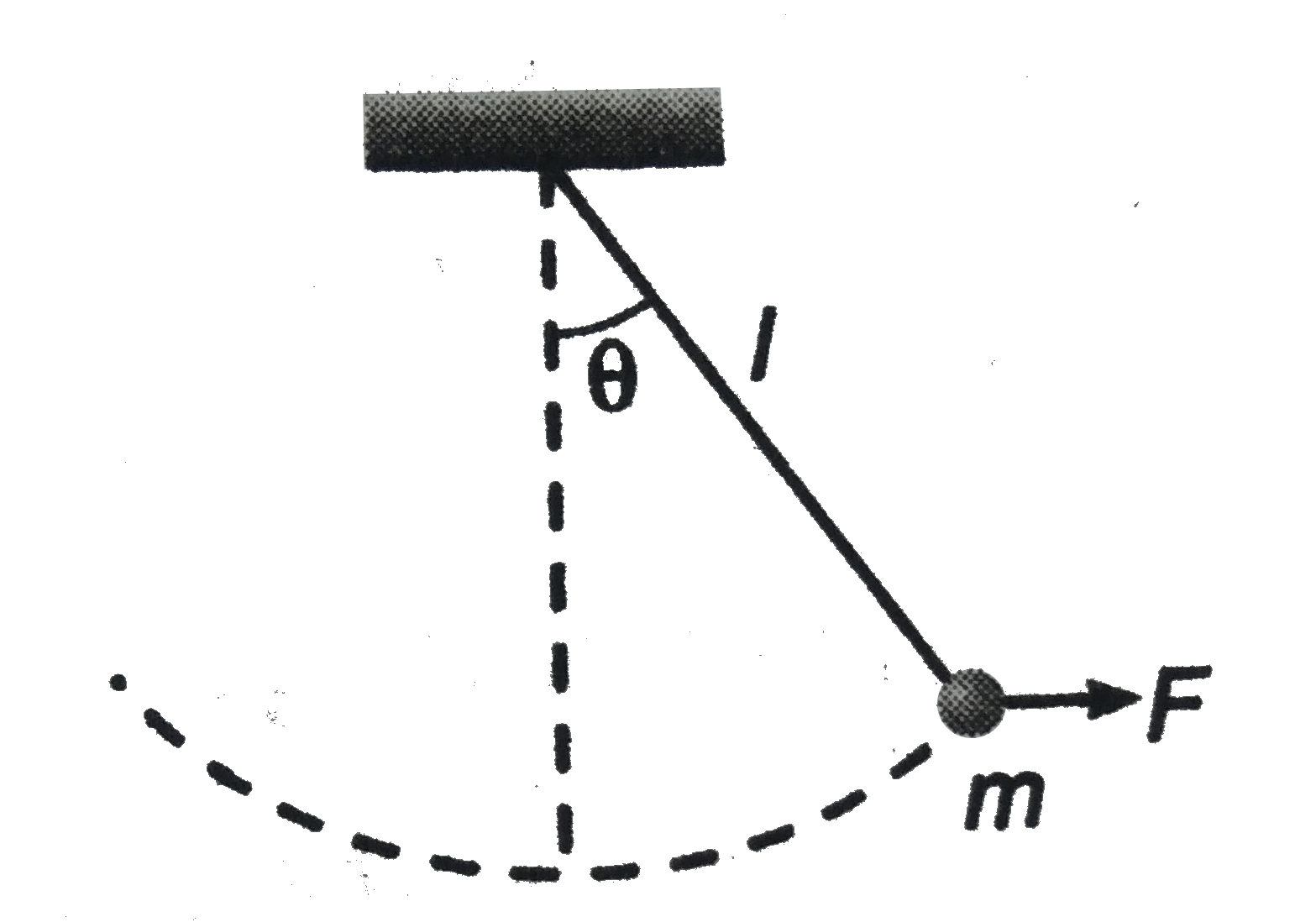 .
.
View SolutionA small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of `theta`.
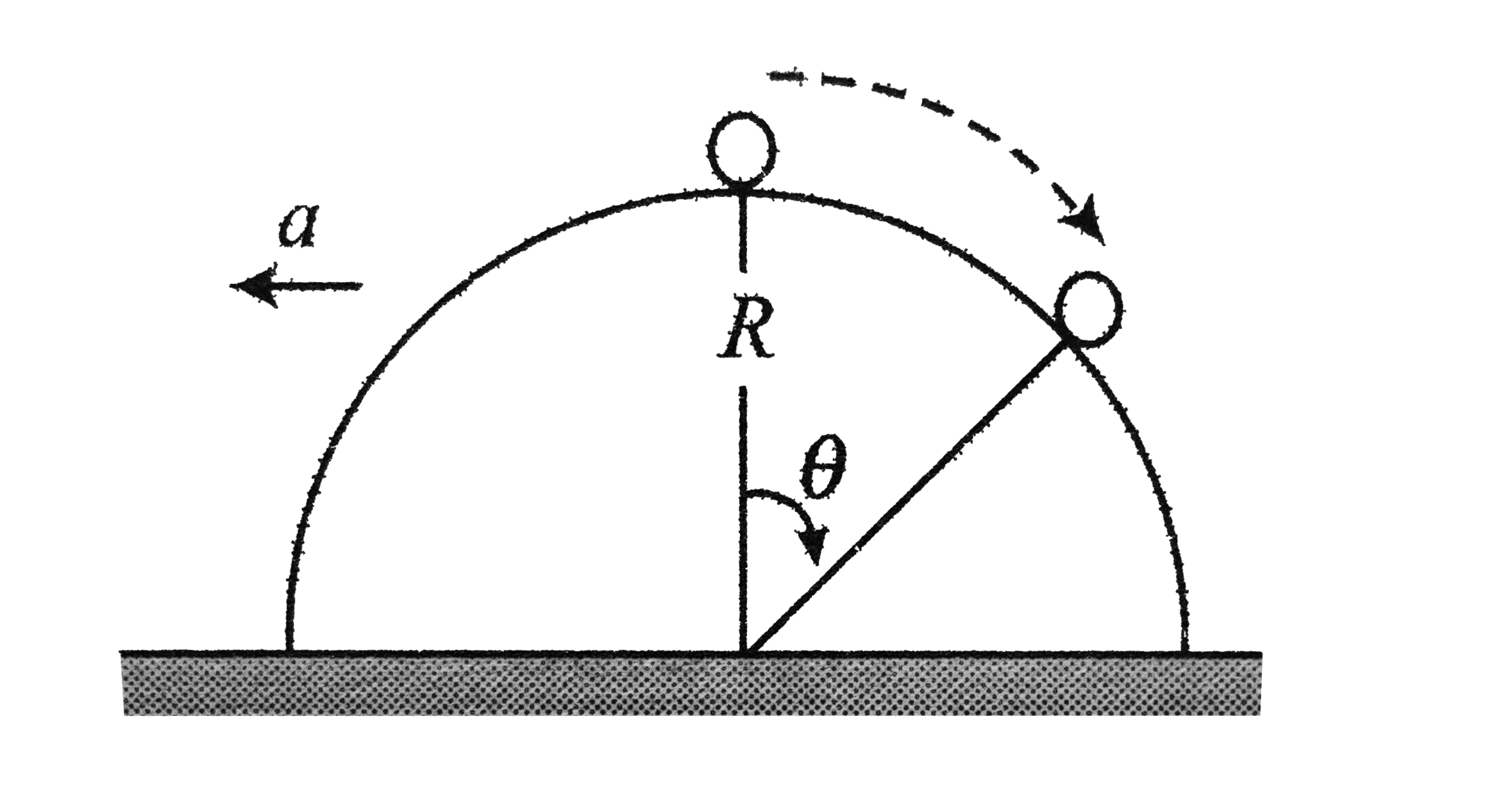
View SolutionA stone of mass 0.4 kg is thrown vertically up with a speed of 9.8 `ms^(-1)`. Find the potential energy after half second.
View SolutionCalculate the work done in lifting a 300N weight to a height of 10m with an acceleration `0.5ms^(-2)`. Take g=`10ms^(-2)`.
View SolutionTwo springs with spring constants ` K _(1) = 1500 N// m`and m `K_(2) = 3000 N//m` are stretched by the same force. The ratio of potential energy stored in spring will be
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest

View SolutionTwo cyllindrical vessels of equal cross sectional ara A contain water upto heights `h_1` and `h_2`. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is `rho`
View SolutionA particle is moving on frictionless XY-plane. It is acted on by a conservative force described by the potential-energy function.
`U(x,y,z)=(1)/(2)k(x^(2)+y^(2)+z^(2))`
where , k=constant
Derive an expression for the force an the particle.
View SolutionA uniform chain of length 4m is kept on a table such that a length of 120 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg What is the work done in pulling the entire chain on the table ?
View SolutionThe potential energy of a conservative force field is given by
`U=ax^(2)-bx`
where, a and b are positive constants. Find the equilibrium position and discuss whether the equilibrium is stable, unstable or neutral.
View SolutionThe potential energy for a conservative force system is given by `U=ax^(2)-bx`. Where a and b are constants find out (a) The expression of force (b) Potential energy at equilibrium.
View SolutionA body of mass 5 kg is thrown vertically up with a kinetic energy of 490 J. What will be height at which the kinetic energy of the body becomes half of the original value ? (Acceleration due to gravity`=9.8ms^(-2)`)
View SolutionA bullet of mass m moving with velocity `upsilon_(1)` strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionA particle of mass m makes SHM in a smooth hemispherical bowl ABC and it moves from A to C and back to A via ABC,so that PB=h. Find the speed of the ball when it just crosses the point B.
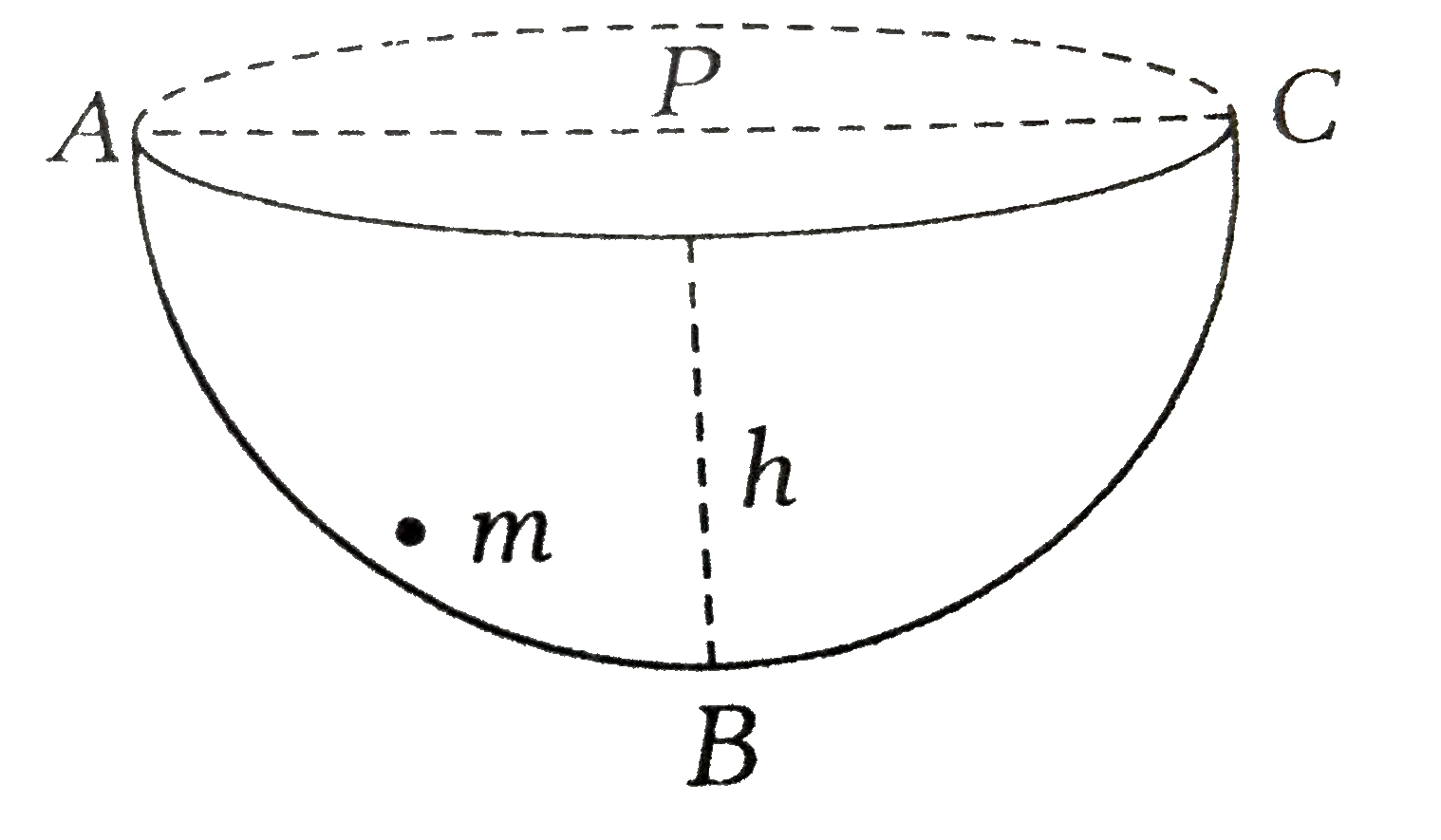
View SolutionA child is swinging a swing. Minimum and maximum heights fo swing from the earth's surface are 0.75 m and 2 m respectively. The maximum velocity of this swing is
View SolutionA machine which is 75 percent efficient, uses 12 joules of energy in lifting up a 1 kg mass through a certain distance. The mass is then allowed to fall through that distance. The velocity at the end of its fall is (in `ms^(-1)`)
View SolutionAuto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of `36 kmh^(-1)` on a smooth road and colliding with a horizontally mounted spring of spring constant `7.5xx10^(3) Nm^(-1)`. Find the maximum compression of the spring .
View SolutionA spherical ball of mass `20kg` is stationary at the top of a hill of height `100m` , it rolls down a smooth surface to the ground , then climbs up another bill of height of `30 m` and final rolls down to a horizontal base at a height of `20 m` about the ground . The velocity attained by the ball is
View SolutionA smooth narrow tube in the form of an arc AB of a circle of centre O and radius r is fixed so that A is vertically above O and OB is horizontal. Particles P of mass m and Q of mass 2 m with a light inextensible string of length (pi r/2) connecting them are placed inside the tube with P at A and Q at B and released from rest. Assuming the string remains taut during motion, find the speed of particles when P reaches B.
 .
.
View SolutionIn the arrangement shown in figure, string is light and inextensible and friction is absent every where. The speed of both blocks after the block `'A'` has ascend a height of `1m` will be `(g=10 m//s^(2))`
View SolutionIn the arrangment shown in figure, `m_(A)`=1 kg, `m_(B)`=4 kg. String is light and inextensible while pulley is smooth. Coefficient of friction between block A and the table is `mu`=0.2. Find the speed of both the blocks when block B has descended a height h=1 m. (Take ,g=10 `ms^(-2)`)

View SolutionConsider the situation shown in figure. The system is released from rest and the block of mass `1 kg` is found to have a speed `0.3 m//s` after it has descended through a destance of `1 m`. Find the coefficient of kinetic friction between the block and the table.
 ,
,
View SolutionA 20 kg body is released from rest so as to slide in between vertical rails and compresses a vertical spring `(k=1920(N)/(m)`) placed at a distance `h=1.0`m from the strating position of the body. The rails offer a frictional force of 40 N opposing the motion of body. Find (a) the velocity v of the body just before striking with the spring, (b) the maximum compression of the spring and (c ) the distance `h^(')` through which the body is rebounded up.
View SolutionCalculate the energy in MeV equivalent to the rest mass of an electron . Given that the rest mass of an electron , `m=9.1 xx 10^(-31) kg`, `1MeV = 1.6 xx 10^(-13) J` and speed of light , `c= 3 xx 10 ^(8) ms ^(-1)`.
View SolutionWhen slow neutrons are incident on a target containing `underset(92)overset(235).U`, a possible fission reaction is
`underset(92)overset(235).U+underset(0)overset(1).nrarr underset(56)overset(141).Ba+underset(36)overset(92).Kr+3_(0)^(1)n`
Estimate the amount of energy released using the following data Given, mass of `underset(92)overset(235).U=235.04 amu`, mass of `underset(0)overset(1).n=1.0087 amu`, mass of `underset(56)overset(141).Ba=140.91 amu`, mass of `underset(36)overset(92).Kr=91.926 amu`, and energy equivalent to 1 amu=931 MeV.
View SolutionA train has a constant speed of 40 `ms^(-1)` on a level road against resistive force of magnitude `3xx10^(4) N`. Find the power of the engine.
View SolutionA machine gun fires 240 bullets per minute. If the mass of each bullet is 10 g and the velocity of the bullets is `600 ms^(-1)`, then find power (in kW) of the gun.
View SolutionIn unloading grain from the hold of a ship, an elevator lifts the grian through a distance of 12 m. Grain is discharged at the top of the elevator at a rate of 2 kg each second and the discharge speed of each of grain particle is 3 `ms^(-1)`. Find the minimum horsepower of the motor that can elevate grain in this way. (Take g=10 `ms^(-2)`)
View SolutionA pump can take out 7200 kg of water per hour from a well 100 m. deep. The power of pump, assuming its efficiency as `50%` will be
View SolutionA block of mass m is pulled by a constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is `mu`. Maximum velocity of the block will be
View SolutionThe force required to row a boat at constant velocity is proportional to the speed. If a speed of 4 `kmh^(-1)` requires 7.5 kW, how much power does a speed of 12 `kmh^(-1)` require?
View SolutionAn engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (Take ,g =10 `ms^(-2)`).
View SolutionAn automobile of mass m accelerates from rest. If the engine supplies a constant power P, the velocity at time t is given by -
View SolutionA train of mass `2xx10^(5)` kg has a constant speed of 20 `ms^(-1)` up a hill inclined at `theta=sin^(-1)((1)/(50))` to the horizontal when the engine is working at `8xx10^(5)` W. Find the resistance to motion of the trian. (Take ,g=9.8 `ms^(-2)`).
View SolutionA small body of mass m moving with velocity `v_(0)` on rough horizontal surface, finally stops due to friction. Find, the mean power developed by the friction force during the motion of the body, if the frictional coefficient `mu`=0.27,m=1 kg and `v_(0)=1.5 ms^(-1)`.
View Solution
EXAMPLE questions and complete solutions for chapter WORK, ENERGY AND POWER of DC PANDEY ENGLISH of Class 11