Complete Solutions to Level 1 Subjective of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
A car is travelling along a circular curve that has a radius of `50m` . If its is speed is `16m//s` and is increasing uniformly at `8m//s^(2)` . Determine the magnitude of its accleration at this instant.
View SolutionA `70kg` man stands in contact against the inner wall of a hollw cylindrical drum of radius `3m` rotating about its verticle axis. The coefficient of friction between the wall and his clothing nis `0.15` . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View SolutionA particle is projected with a speed u at angle `theta` with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circle? This radius is called the adius of curvature of the curve at the point.
View SolutionFind the maximum speed at which a truck can safely travel without toppling over, on a curve of radius `250m` . The height of the centre of gravity of the truck above the ground is `1.5m` and the distance between the wheels is `1.5m` , the truck being horizontal.
View SolutionA hemispherical bowl of radius R si set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is `theta`, find the angular speed at which the bowl is rotating.
View SolutionShow that the angle made by the string with the vertical in a conical pendulum is given by `costheta=(g)/(Lomega^(2))` , where `L` is the string and `omega` is the angular speed.
View SolutionA boy whirls a stone of small mass in a horizontal circle of radius `1.5m` and at height `2.9m` above level ground. The string breacks and the stone flies off horizontally and strikes the ground after travelling a horizontal distance of `10m` . What is the magnitude of the centripetal acceleration of the stone while in circular motion ?
View SolutionA block of mass m is kept on a horizontal ruler. The friction of coefficient between the ruler and the block is `mu`. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. a. What can the maximum angular speed of the ruler b) if the angular speed of ruler is uniformly increased from zero to an angular acceleration `alpha` , at what angular speed will the block slip?
View SolutionA thin circular wire of radius `R` rotates about its vertical diameter with an angular frequency `omega` . Show that a small bead on the wire remain at its lowermost point for `omegalesqrt(g//R)` . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega=sqrt(2g//R)` ? Neglect friction.
View SolutionTwo block tied with a massless string of length `3m` are placed on a rotating table as shown. The axis of rotation is `1m` from `1kg` mass and `2m` from `2kg` mass. The angular speed `omega=4rad//s` . Ground below `2kg` block is smooth and below `1kg` block is rough. `(g=10m//s^(2))`
(a) Find tension in the string, force of friction on `1kg` block and its direction.
(b) If coefficient of friction between `1kg` block and groung is `mu=0.8`. Find maximum angular speed so that neither of the blocksd slips.
(c) If maximum tension in the string can be `100N` , then maximum angular speed so that neither of the blocks slips.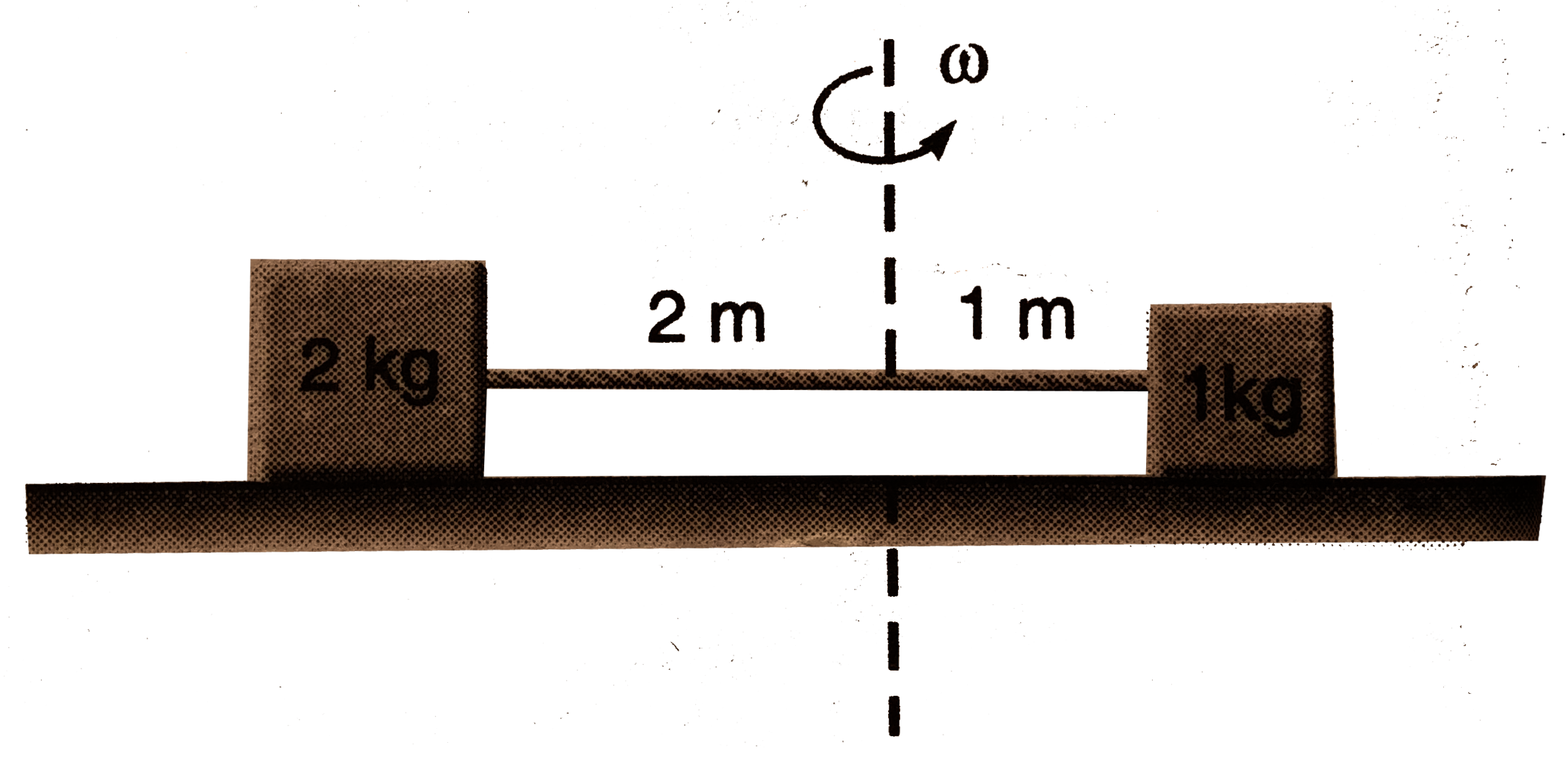
View SolutionA small block slides with velocity `0.5sqrt(gr)` on the horizontal frictionless surface as shown in the figure. The block leaves the surface at point `C` . Calculate angle `theta` in the figure.
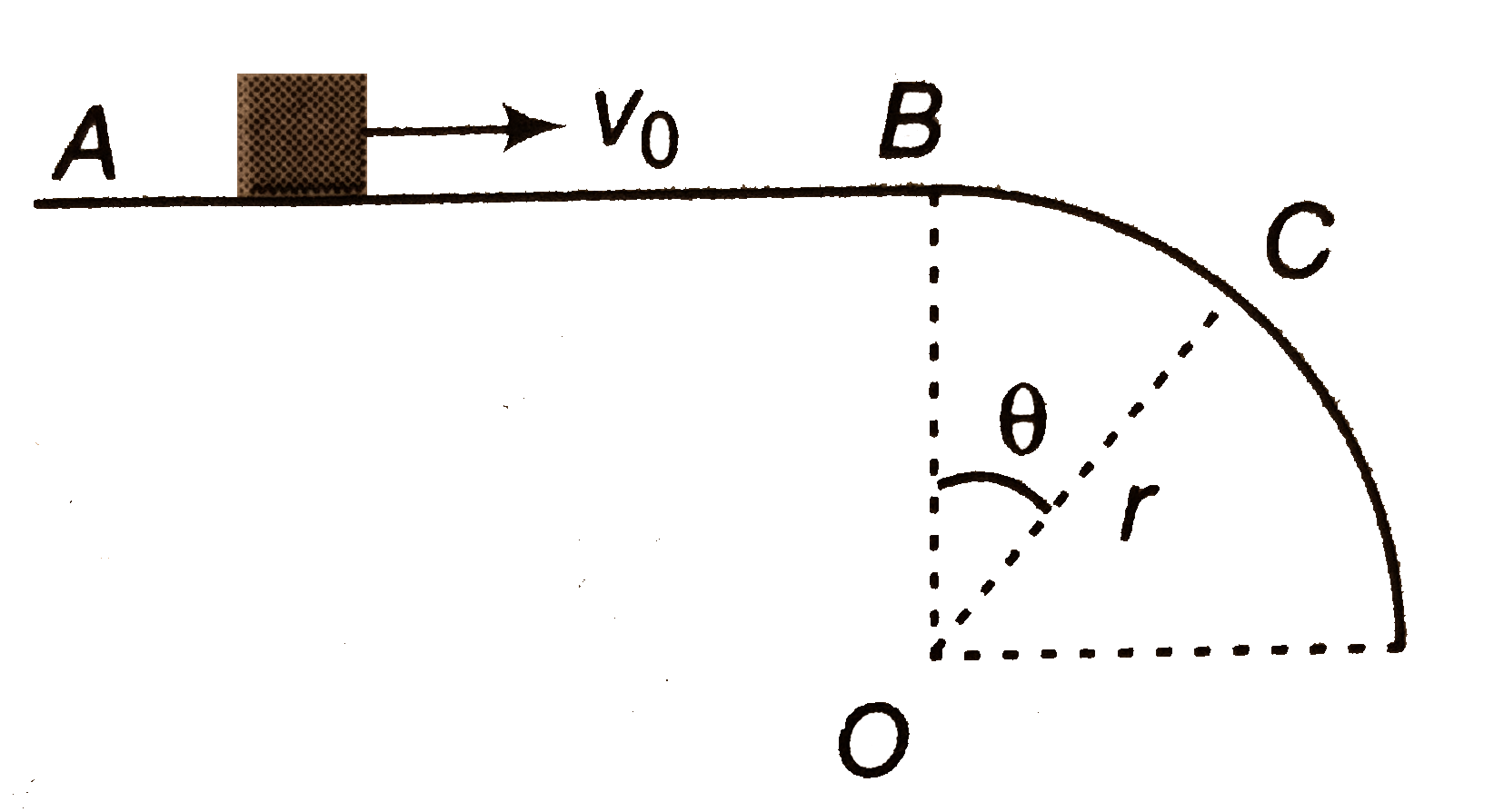
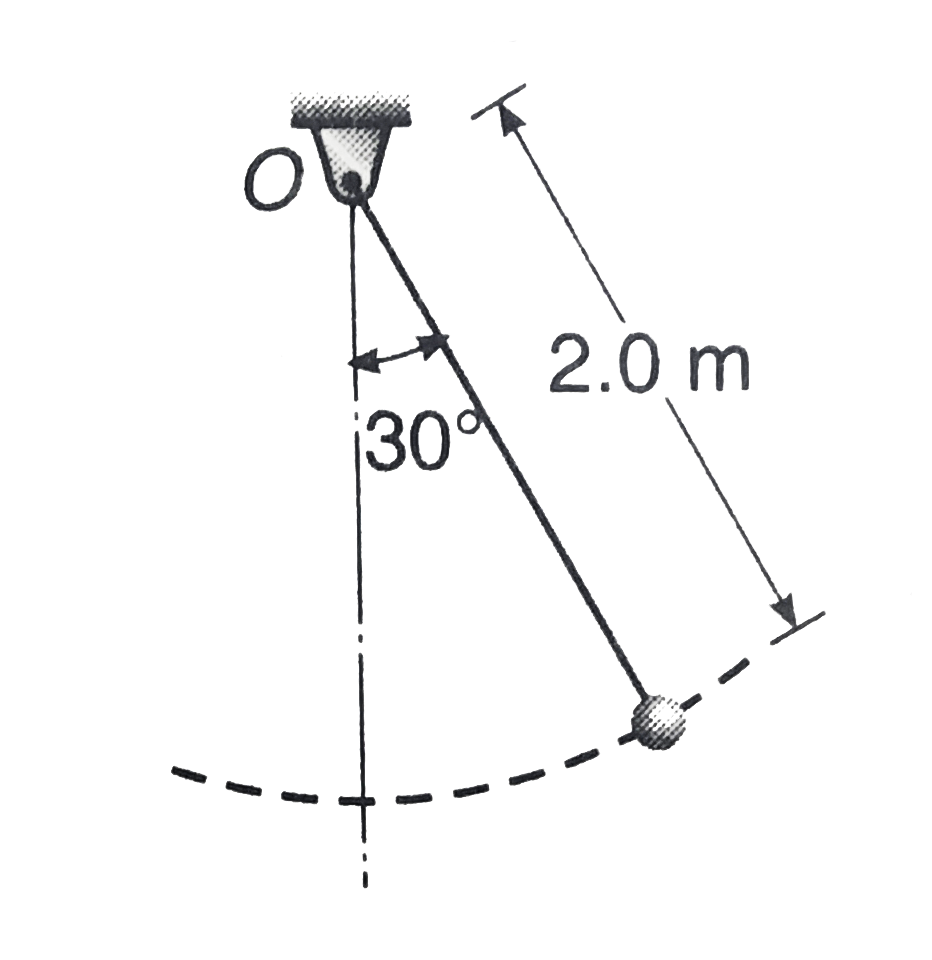
View SolutionThe bob of the pendulum shown in figure describes an arc of a circle in a vertical plane. If the tension in the cord is `2.5` times the weight of the bob for the position shown. Find the velocity and the acceleration of the bob in that position.
View SolutionThe sphere at `A` is given a downward velocity `v_(0)` of magnitude `5m//s` and swings in a vertical plane at the end of a rope of length `l=2m` attached to a support at `O` . Determine the angle `theta` at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
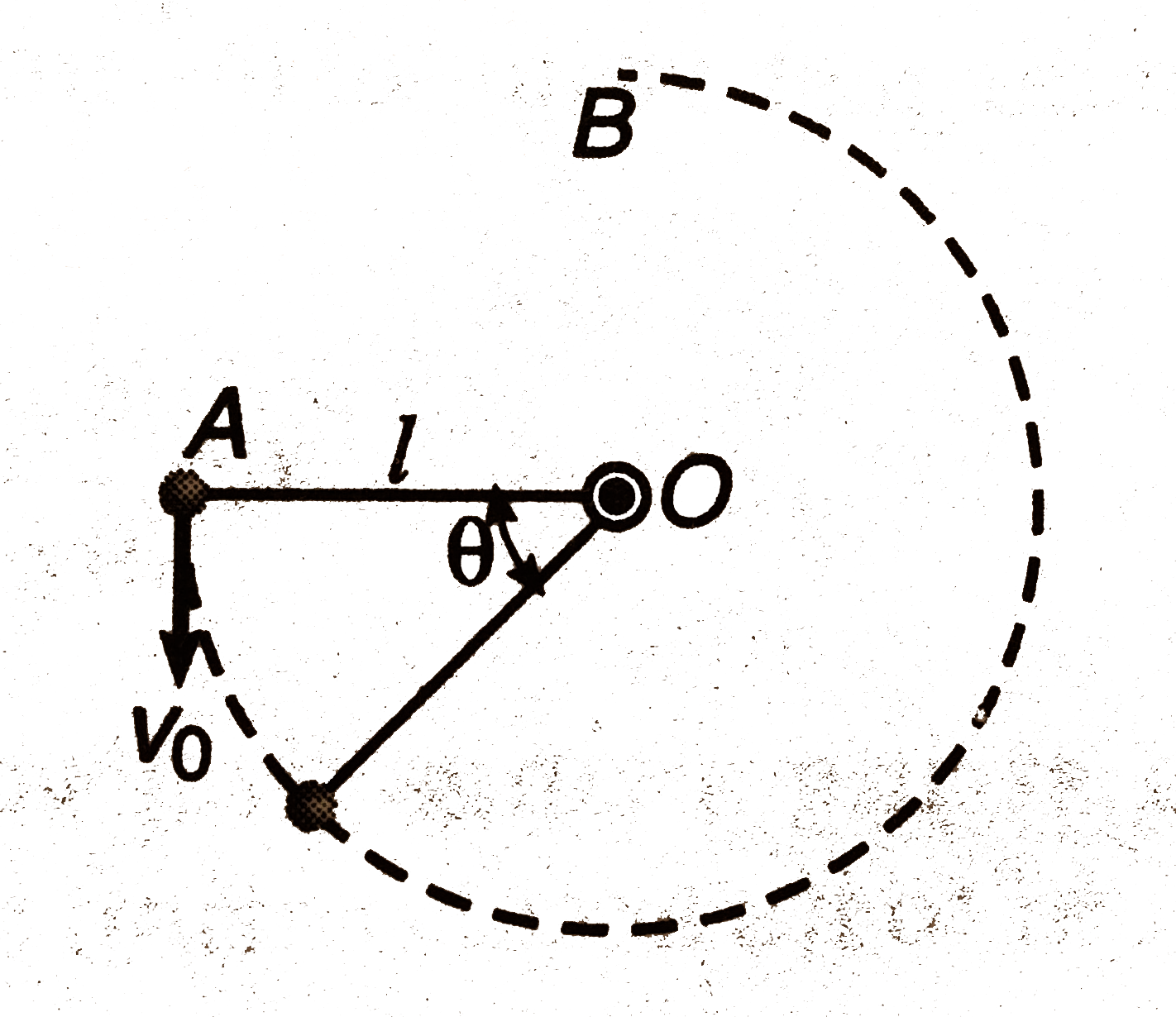
View Solution
Level 1 Subjective questions and complete solutions for chapter CIRCULAR MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS CIRCULAR MOTION
- Assertion And Reason
- Check point
- Comprehension
- Example
- Exercise 10.1
- Exercise 10.2
- Exercise 10.3
- Integer
- JEE Advanced
- JEE Main
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Matrix Matching
- Medical entrances s gallery
- Miscellaneous Examples
- More than One Option is Correct
- Solved Examples
- Subjective Questions
- Taking it together