Complete Solutions to JEE Main of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | JEE Main |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed `omega` varries with time t is
View SolutionA particle moves in `x-y` plane according to the law `x = 4 sin 6t and y = 4 (1-cos 6t)`. The distance traversed by the particle in 4 second is (`x & y` are in meters)
View SolutionA `x and y` co-ordinates of a particle are `x=A sin (omega t) and y = A sin(omegat + pi//2)`. Then, the motion of the particle is

View SolutionPosition vector of a particle moving in `x-y` plane at time `t` is `r=a(1- cos omega t)hat(i)+a sin omega t hat(j)`. The path of the particle is
View SolutionStarting from rest, a particle rotates in a circle of radius R = `sqrt 2 m` with an angular acceleration = `pi/4` rad/s2.The magnitude of average velocity of the particle over the time it rotates quarter circle is:
View SolutionA bob hangs from a rigid support by an inextensible string of length `l`. If it is displaced through a distance `l` (from the lowest position) keeping the string straight and then released. The speed of the bob at the lowest position is

View SolutionA particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
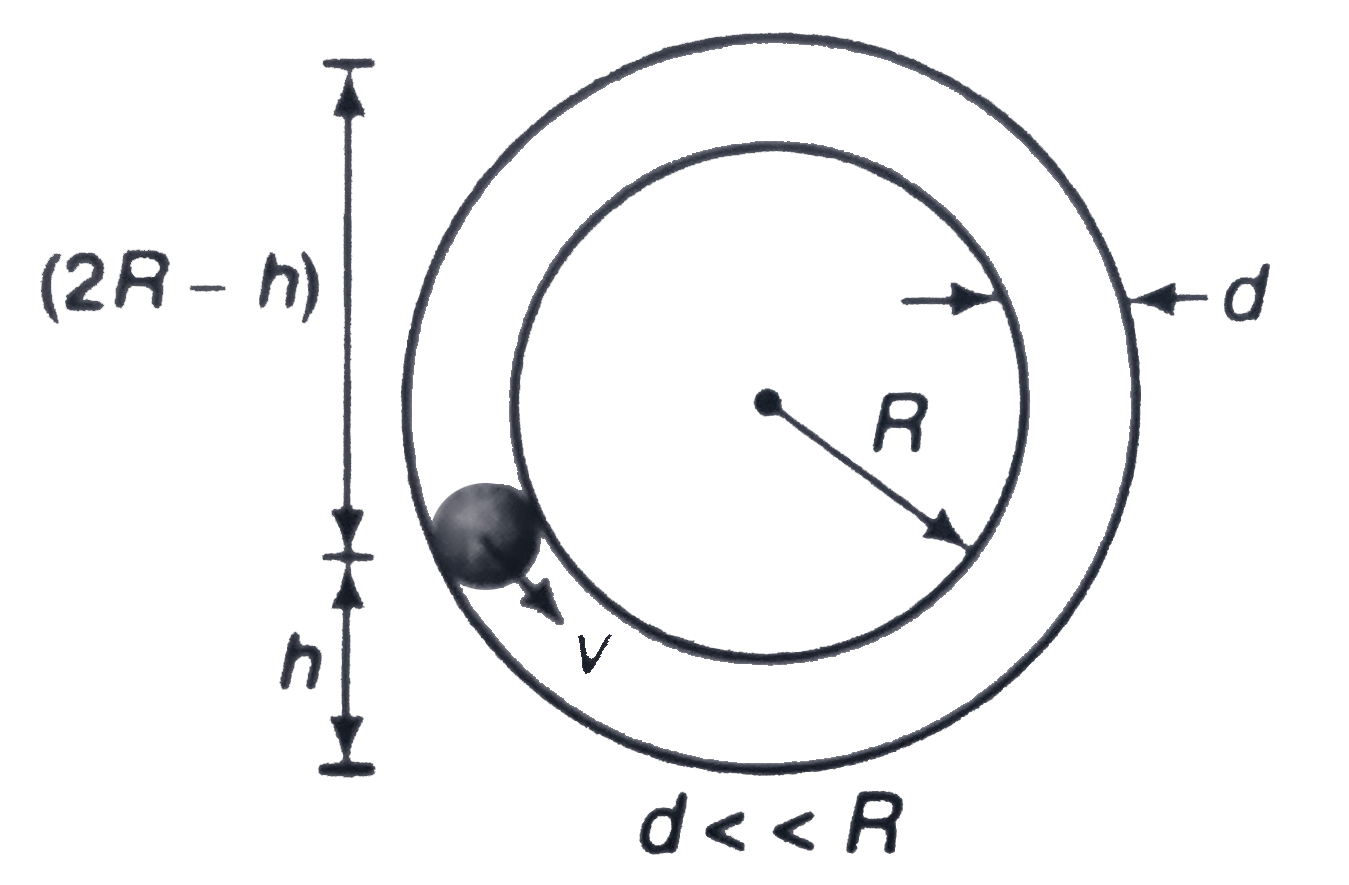
View SolutionWith what minimum speed `v` must a small ball should be pushed inside a smooth vertical tube from a height `h` so that it may reach the top of the tube? Radius of the tube is `R` .
View SolutionThe second's hand of a watch has length 6 cm. Speed of end point and magnitude of difference of velocities at two perpendicular positions will be
View SolutionA pendulum bob is swinging in a vertical plane such that its angular amplitude is less than `90^(@)`. At its highest point, the string is cut. Which trajectory is possible for the bob afterwards ?
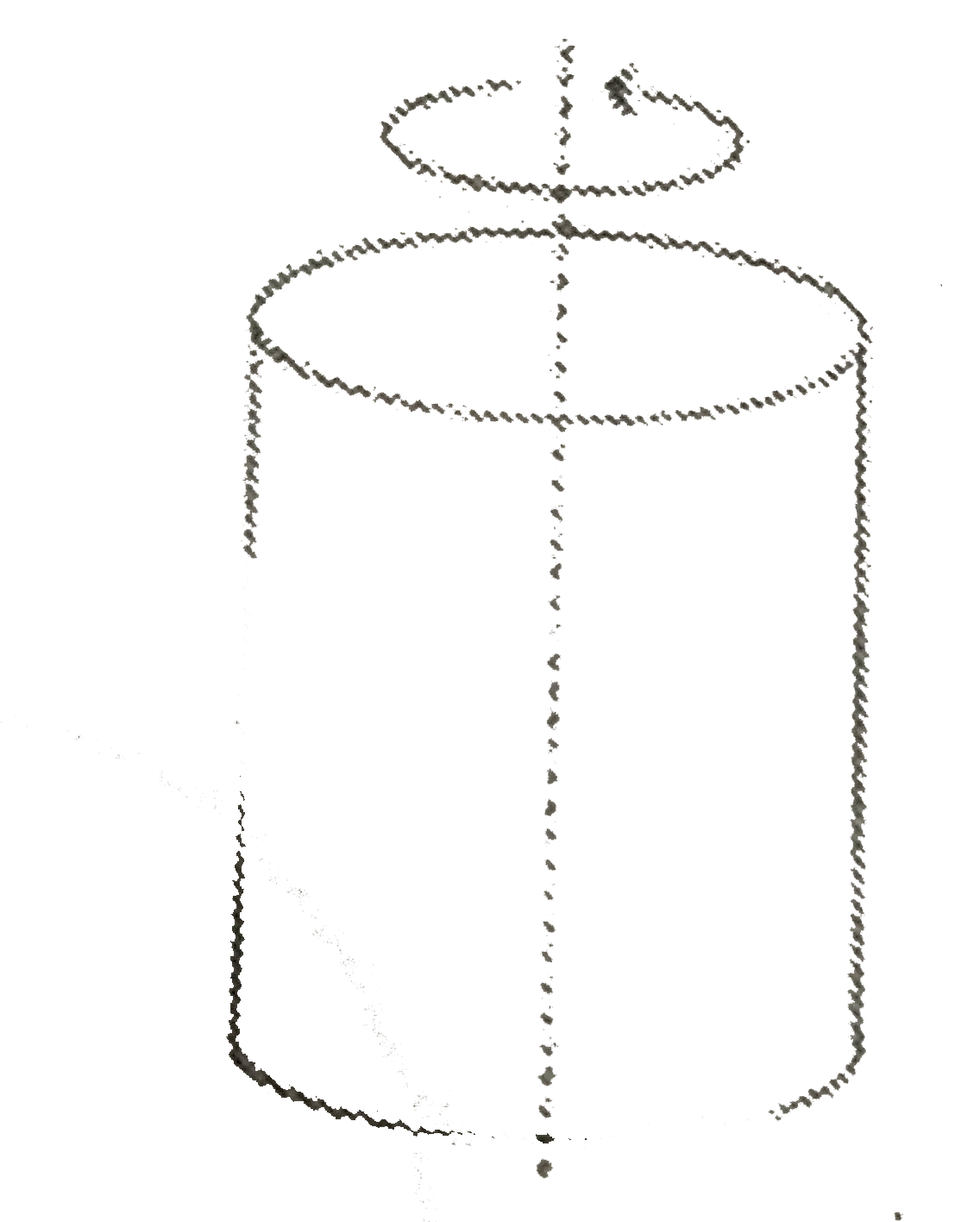
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity `omega` about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
View SolutionA bob of mass m attached to an inextensible string of length l is suspended from a verticle support. The bob rotates in a horizontal circle with an angular speed `omega "rad"//s` about the verticle. About the point of suspension.
View SolutionA particle of mass `m` attached to a string of length `l` is descending circular motion on a smooth plane inclined at an angle `alpha` with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
View SolutionA pendulum of mass 1 kg and length = 1m is released from rest at angle = 60º. The power delivered by all the forces acting on the bob at angle = 30º will be: (g = 10 m/s2)
View Solution(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle `θ` of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as `T = as^(2)` , where 'a' is a constant. Find the force acting on the particle as a function of s.
View SolutionA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle `alpha`. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle `theta` which the string makes with the vertical after hitting the pin is

View SolutionA particle moves along a circle if radius `(20 //pi) m` with constant tangential acceleration. If the velocity of the particle is ` 80 m//s` at the end of the second revolution after motion has begun the tangential acceleration is .
View SolutionThe velocity and acceleration vectors of a particle undergoing circular motion are `v = 2 hat(i) m//s and a = 2 hat(i)+4 hat(j)m//s^(2)` respectively at some instant of time. The radius of the circle is
View SolutionA particle mass `m` begins to slide down a fixed smooth sphere from the top of its vertical diameter. Calculate its tangential acceleration, radial acceleration and total acceleration when it breaks off.
View SolutionA car is moving in a circular horizontal track of radius 10 m with a constant speed of `10ms^(-1)`. A plumb bob is suspended from the roof of the car by a light rigid rod of length 1 m. The angle made by the rod with track is
View SolutionTwo identical balls 1 and 2 are tied to two strings as shown in figure. They are rotated about point O. Ball 1 is observed from ball 2, centrifugal force on ball 1 is `F_(1)`. Similarly, ball 2 is observed from ball 1 and centrifugal force on ball 2 is `F_(2)`, then

View SolutionA particle starts moving from rest at `t=0` with a tangential acceleration of constant magnitude of `pi m//s^(2)` along a circle of radius 6 m. The value of average acceleration, average velocity and average speed during the first `2 sqrt(3)` s of motion, are respectively :
View SolutionA uniform disc of radius 'R' is rotating about vertical axis passing through the centre in horizontal plane with constant angular speed. A massless pole AB is fixed on its circumference as shown in the figure. A light string of length 2R is tied at A and a small bob at its other end. In equilibrium string makes an angle `37^(@)` with vertical. The angular speed of disc is `("take" R=(3)/(11)m,g=10m//s^(2))`

View Solution
JEE Main questions and complete solutions for chapter CIRCULAR MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS CIRCULAR MOTION
- Assertion And Reason
- Check point
- Comprehension
- Example
- Exercise 10.1
- Exercise 10.2
- Exercise 10.3
- Integer
- JEE Advanced
- JEE Main
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Matrix Matching
- Medical entrances s gallery
- Miscellaneous Examples
- More than One Option is Correct
- Solved Examples
- Subjective Questions
- Taking it together