Complete Solutions to Example of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY | Example |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
A particle moves in a circular path of radius `0.5 m` at a speed that uniformly increases. Find the angular acceleration of particle if its speed changes from `2.0m//s` to `4.0 m//s` in `4.0s`
View SolutionThe speed of a particle moving in a circle of radius `r=2m` varies with time `t` as `v=t^(2)`, where `t` is in second and `v` in `m//s`. Find the radial, tangential and net acceleration at `t=2s`.
View SolutionIn circular motion, what are the possible values (zero, positive or negative) of the following:
(a) `omega.v` (b) `v.a`, (c) `omega.alpha`
View SolutionA small block of mass `100 g` moves with uniform speed in a horizontal circular groove, with vertical side walls of radius `25cm`. If the block takes `2.0 s` to complete one round, find the constant force by the side wall of the groove.
View SolutionA fighter plane is pulling out for a dive at a speed of `900 km//h`. Assuming its path to be a vertical circle of radius `2000 m` and its mass to be `16000 kg`, find the force exerted by the air on it at the lowest point. Take `g=9.8 m//s^(2)`
View SolutionThree particles, each of the mass `m` are situated at the vertices of an equilateral triangle of side `a`. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation `a`. Find the initial velocity that should be given to each particle and also the time period of the circular motion. `(F=(Gm_(1)m_(2))/(r^(2)))`
View Solution(a) How many revolutions per minute must the apparatus shown in figure make about a vertical axis so that the cord makes an angle of `45^(@)` with the vertical ?

(b)What is the tension in the cord then? Given, `l=sqrt(2)m,a=20 cm` and `m=5.0 kg`?
View SolutionA turn of radius `20 m` is banked for the vehicle of mass `200 kg` going at a speed of `10 m//s`. Find the direction and magnitude of frictional force (a) `5 m//s`
(b) `15 m//s`
Assume that friction is sufficient to prevent slipping. `(g=10 m//s^(2))`
View SolutionA particle of mass `m` is placed over a horizontal circular table rotating with an angular velocity `omega` about a vertical axis passing through its centre. The distance of the object from the axis is `r`. Find the force of friction `f` between the particle and the table.
View SolutionTwo blocks `A` and `B` of masses `1 kg` and `3 kg` are attached with two massless strings as shown in figure. The system is kept over a smooth table and it is rotates about the axis shown in figure with constant angular speed `omega=2 rad//s`. Find direction and magnitude of centrifugal force on
(a) A as observed by `B`
(b) `B` as observed by `A`

View SolutionA stone tied to a string of length `L` is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at lowest position and has a speed `u` . Find the magnitude of the change in its velocity as it reaches a position, where the string is horizontal.
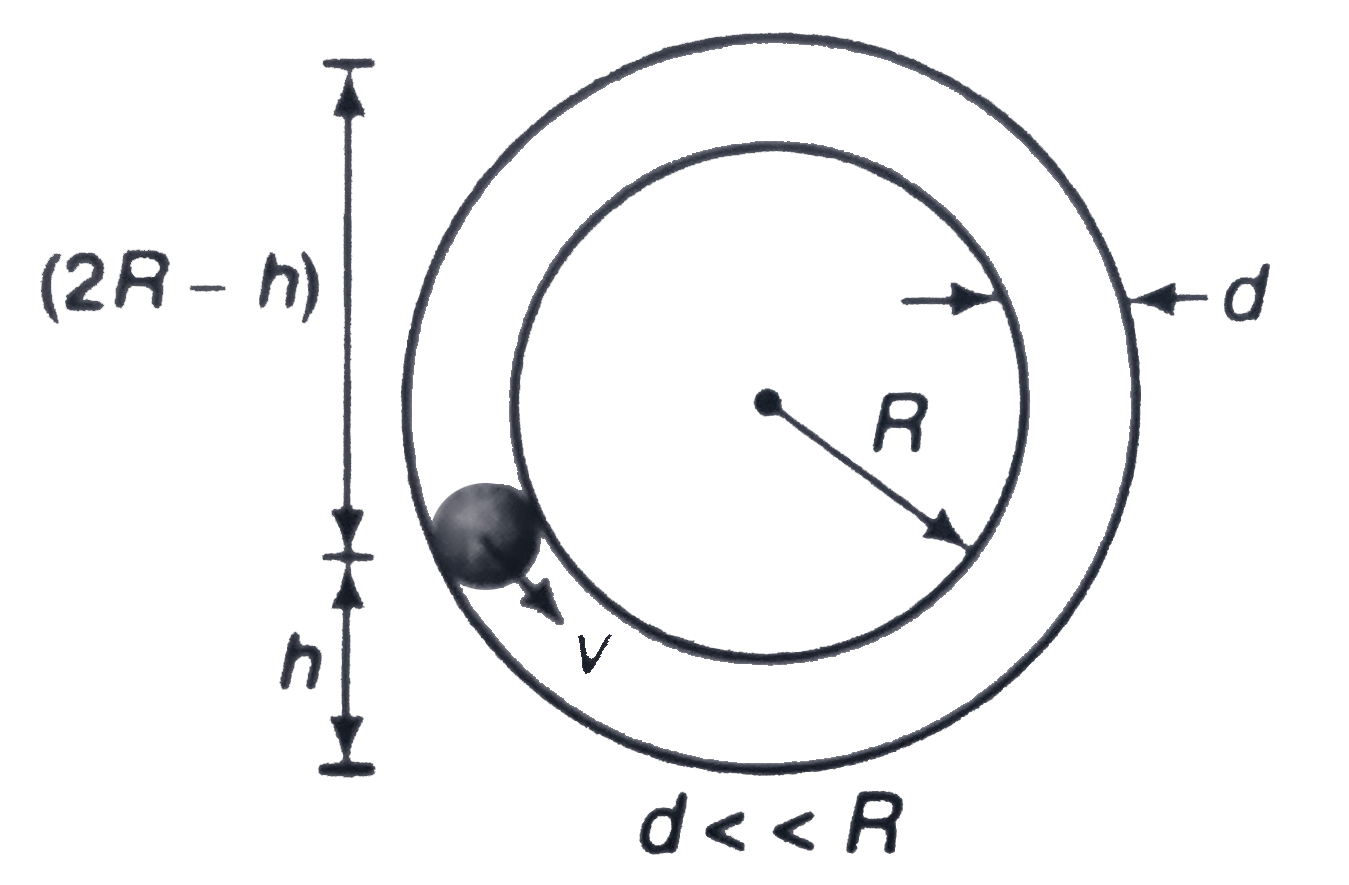
View SolutionWith what minimum speed `v` must a small ball should be pushed inside a smooth vertical tube from a heoght `h` so that it may reach the top of the tube? Radius of the tube is `R` .
View SolutionA particle is suspended from a fixed point by a string of lengh `5m`. It is projected from the equilibrium position with such a velocity that the string slakens after the particle has reached a height `8m` above lowest point. Find the velocity of the particle, just before the string slackens.
Find also, to what to what height the particle can rise further?
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length `l` is projected horizonally with speed `sqrt(gl)` . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionCalculate the average angular velocity of the hour hand of the of a clock.
View SolutionAn object revolves uniformly in a circle of diameter `0.80` m and completes 100 rev `"min"^(-1)`. Find its time period and angular velocity.
View SolutionOne end of a cylindrical glass rod (mu = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (mu= 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
View SolutionA particle moves in a circle of radius 4 m with a linear velocity of `20ms^(-1)`. Find the angular velocity.
View SolutionIf the length of the second's hand in a stop clock is 3 cm the angular velocity and linear velocity of the tip is
View SolutionA point on the rim of a disc starts circular motion from rest and after time t, it gains an angular acceleration given by `alpha=3t-t^(2)`. Calculate the angular velocity after 2 s.
View SolutionThe wheel of a motor rotates with a constant acceleration of `4" rad s"^(-1)`. If the wheel starts form rest, how many revolutions will it make in the first 20 second?
View SolutionThe wheel of a car, accelerated uniformly from rest, rotates through `1.5` rad during the first second. Find the angle rotated during the next second.
View SolutionFind the magnitude of the centripetal acceleration of a particle on the tip of a blade, ` 0 .30 ` metre in diameter, rotating at `1200` revolution per minute.
View SolutionFind the acceleration of a particle placed on the surface of the earth at the equator, due to the earth rotation. The radius of earth is 6400 km and time period of revolution of the earth about its axis is 24 h.
View SolutionConsider
 .
.
The potential difference `V_(A)-V_(B)` is.
View SolutionA particle moves in a circular path of radius `0.5 m` at a speed that uniformly increases. Find the angular acceleration of particle if its speed changes from `2.0m//s` to `4.0 m//s` in `4.0s`
View SolutionA car is travelling along a circular curve that has a radius of `50m` . If its speed is `16m//s` and is increasing uniformly at `8m//s^(2)` . Determine the magnitude of its acceleration at this instant.
View SolutionThe speed of a particle moving in a circle of radius `r=2m` varies with time `t` as `v=t^(2)`, where `t` is in second and `v` in `m//s`. Find the radial, tangential and net acceleration at `t=2s`.
View SolutionA particle moves in a circle of radius `2 cm` at a speed given by `v = 4t`, where `v` is in `cm s^-1` and `t` is in seconds.
(a) Find the tangential acceleration at `t = 1 s`
(b) Find total acceleration at `t = 1 s`.
View SolutionA catlyst is riding with a speed of 27 km/h. As he approaches a circular turn on the raod of radius 80m, he applies brakeks and reduces his speed at the constant rate of 0.50m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
View SolutionA ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving in a horizontal circle. The string will break if the tension is more than 25 N . What is the maximum speed with which the ball can be moved
View SolutionA spaceman in training is rotated in a seat at the end of a horizontal arm of length 5 m. If he can with stand acceleration upto 9 g, then what is the maximum number of revolution per second permissible? (Take, g =`10ms^(-2)`)
View SolutionA string breaks under a load of 4.8kg A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle . Calculate the greatest number of revolutions that the mass can make without breaking the string .
View SolutionA ball of mass `0.12` kg is being whirled in a horizontal circle at the end of a string `0.5` m long. It is capable of making 231 revolutions in one minute. Find the breaking tension of the string
View SolutionA gramophone disc rotates at 60 rpm . A coin of mass 18 g is placed at a distance of 8 cm from the centre . Calculate centrifugal force on the coin . Take `pi^(2) = 9. 87` .
View SolutionFind the maximum speed at which a car can take turn round a curve of 30 cm radius on a level road if the coefficient of friction between the tyres and the road is 0.4. Take `g = 10 ms^(-2)`.
View SolutionA cyclist speeding at `4.5"km h"^(-1)` on a level road takes a sharp circular turn of radius 3 m without reducing the speed The coefficient of static friction between the road and the tyres is `0.1` will the cyclist slip while taking the turn (i) with a speed of `405"km h"^(-1)` and (ii) with a speed of `9 "km k^(-1)`?
View SolutionA turn of radius 600 m is banked for a vehicle of mass 200 kg going with a speed of `180kmh^(-1)` . Determine the banking angle of its path.
View SolutionA train has to negotiate a curve of radius 2000 m. By how much should the outer rail be raised with respect to inner rail for a speed of `72"km h^(-1)`. The distance between the rails is 1 m.
View SolutionA circular racetrack of radius 300 m is banked at an angle of `15^(@)` The coefficient of friction between the wheels of a race car and the road is 0.2. The optimum speed of the race car to avoid wear and tear on its tyres is
View SolutionA cyclist speeding at `6ms^(-1)` in a circle of 18 m radius makes an angle `theta `with the vertical. Calculate `theta`. Also determine the minimum possible value of the coefficient of friction between the tyres and the ground?
View SolutionA body of mass `200g` tied to one end of string is revolved in a horizontal circle of radius `50cm` with angular speed `60` revolution per minute `("rpm")` on a smooth horizontal surface. Find (a) linear speed, (b) the acceleration and ( c) tension in the sting. what will happen if string is broken? (Take `pi^(2)=10)`
View SolutionA ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in radian/s) is:
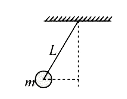
View SolutionA boy whirls a stone of small mass in a horizontal circle of radius `1.5m` and at height `2.9m` above level ground. The string breaks and the stone flies off horizontally and strikes the ground after travelling a horizontal distance of `10m` . What is the magnitude of the centripetal acceleration of the stone while in circular motion ?
View SolutionIN a rotor, a hollow verticla cylindrical structure rotates about its axis and a person rests asgainst he inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the roter is 2m and the coefficient of static frictioin between the wall and theperson is 0.2, find the minimum speed at which the floor may be removed Take `g=10 m/s^2`.
View SolutionOne end of a string of length 1 m is tied to a body of mass `0.5` kg. It is whirled in a vertical circle with angular frequency 4 rad/s. The tension in the string, when the body is at lower most point of its motion, will be equal to (take, g = 10 `ms^(-1)`)
View SolutionA ball of mass `0.6 kg` attached to a light inextensible string rotates in a vertical circle of radius `0.75 m` such that it has speed of `5 ms^(-1)` when the string is horizontal. Tension in the string when it is horizontal on other side is `(g = 10 ms^(-2))`.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle `theta` with the vertical. Find the tension in the string at this instant.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA particle of mass m is attached to a string of length L and given velocity `sqrt(10gL)` in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
View SolutionA hemispherical bowl of radius R si set rotating abouv its axis of symmetry whichis kept vertical. A small blcok kept in the bowl rotates with the bowl without slippingn on its surface. If the surfaces of the bowl is mooth, and the abgel made by the radius through the block with the vertical is `theta`, find the angular speed at which the bowl is rotating.
View Solution
Example questions and complete solutions for chapter CIRCULAR MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS CIRCULAR MOTION
- Assertion And Reason
- Check point
- Comprehension
- Example
- Exercise 10.1
- Exercise 10.2
- Exercise 10.3
- Integer
- JEE Advanced
- JEE Main
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Matrix Matching
- Medical entrances s gallery
- Miscellaneous Examples
- More than One Option is Correct
- Solved Examples
- Subjective Questions
- Taking it together