Complete Solutions to Assertion And Reason of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY | Assertion And Reason |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Assertion: A particle is rotating in a circle with constant speed as shown. Between point `A` and `B` , ratio of average acceleration and average velocity `v` can be stopped in a minimum distance `d` . If the same car, moving with same speed `v` takes a circular turn, then minimum safe radius can be `2d` .
Reasion: `d=(v_(2))/(2mug)` and minimum safe radius `=(v_(2))/(mug)`
View SolutionAssertion: A particle is rorating in a circle with constant speed as shown. Between point `A` and `B` , ratio of average acceleration and average velocity is angular velocity of particle about point `O` .
Reason: Since speed is constant, angular velocity is also constant.
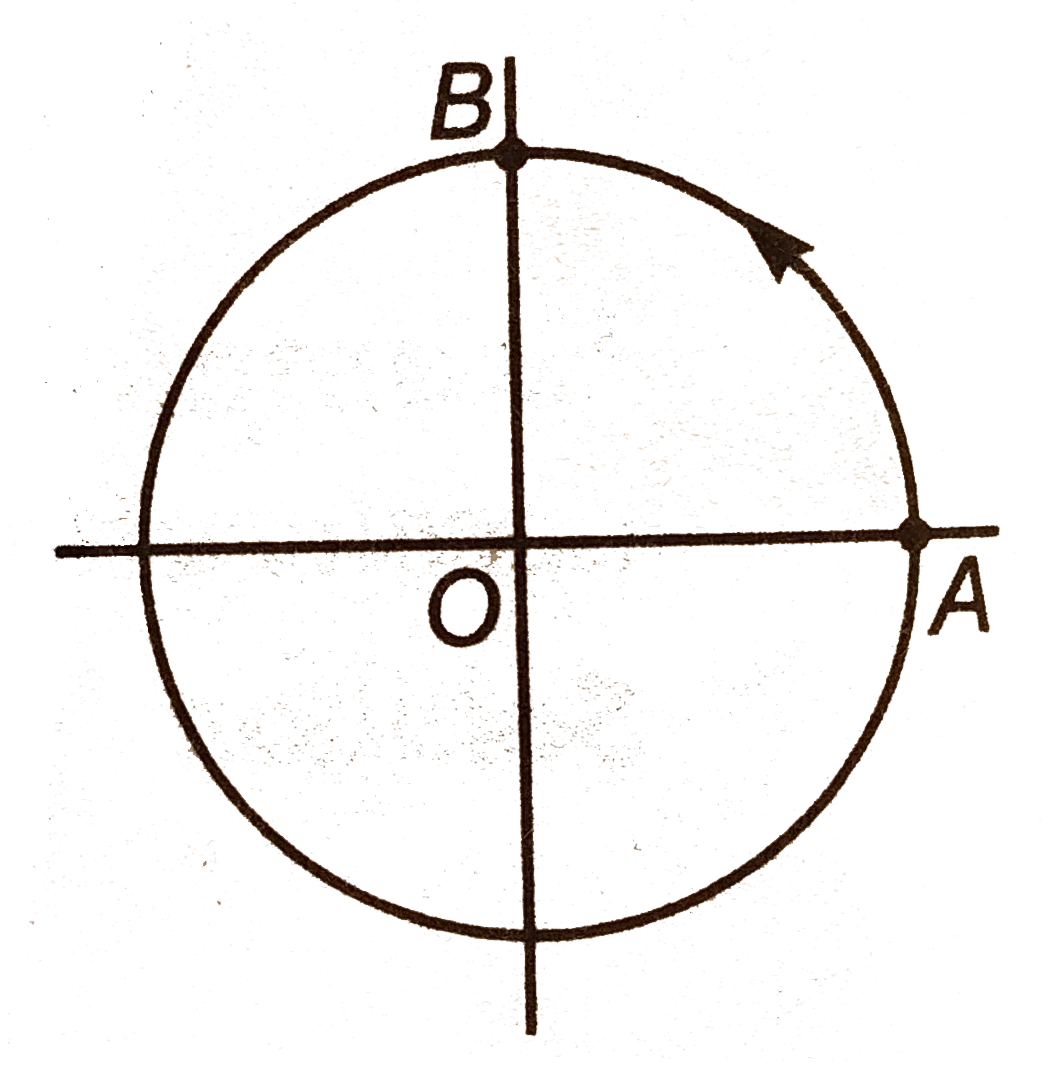
View SolutionAssertion: A frame moving in a circle with constant speed can never be an inertial frame.
Reason: It has a constant acceleration.
View SolutionAssertion: In circular motion, dot product of velocity vector `(v)` and acceleration vector `(a)` may be positive, negative or zero.
Reason: Dot product of angular velocity vector and linear velocity vector is always zero.
View SolutionAssertion: Velocity and acceleration of a particle in circular motion at some instant are:
`v=(2hat(i))ms^(-1)` and `a=(-hat(i)+2hat(j))ms^(-2)` , then radius of circle is `2m` .
Reason: Speed of particle is decreasing at a rate of `1ms^(-2)` .
View SolutionAssertion: In vertical circular motion, acceleration of bob at position `A` is greater than `'`g'` .

Reason: Net acceleration at `A` is resultant of tangential and radial components of acceleration.
View SolutionAssertion: A pendulam is oscillating between points `A` , `B` and `C` . Acceleration of bob at points `A` or `C` is zero.
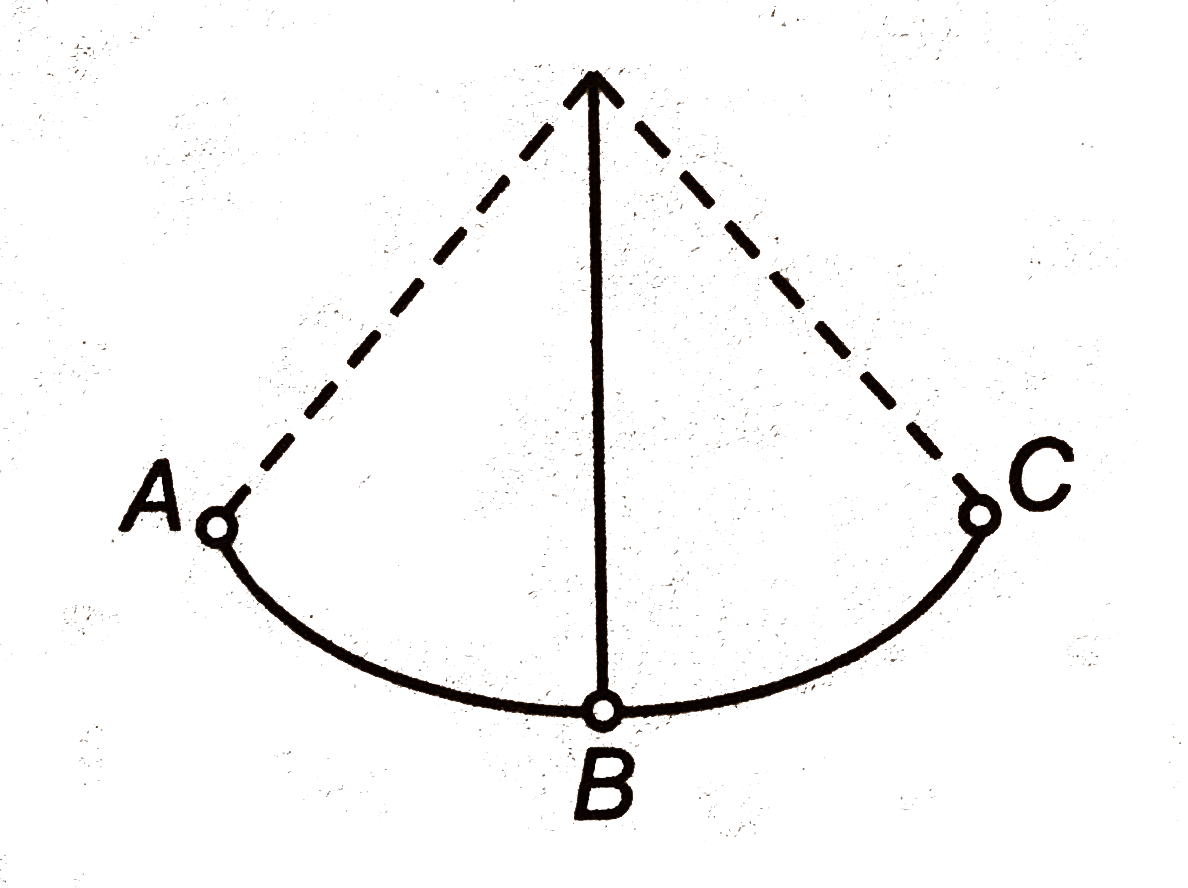
Reason: Velocity at these points is zero.
View SolutionAssertion: Speed of a particle moving in a circle varies with time as, `u=(4t-12)` . Such type of circular motion is not possible.
Reason: Speed cannot change linearly with time.
View SolutionAssertion: Circular and projectile motions both are two idimensional motion.But In circular motion, we cannot apply `v=u+at` directly, whereas in projectile motion we can.
Reason: Projectile motion takes place under gravity, while in circular motion gravity has no role.
View SolutionAssertion: A particle of mass `m` takes uniform horizontal circular motion inside a smooth funnel as shown. Normal reaction in this case is not `mgcostheta` .
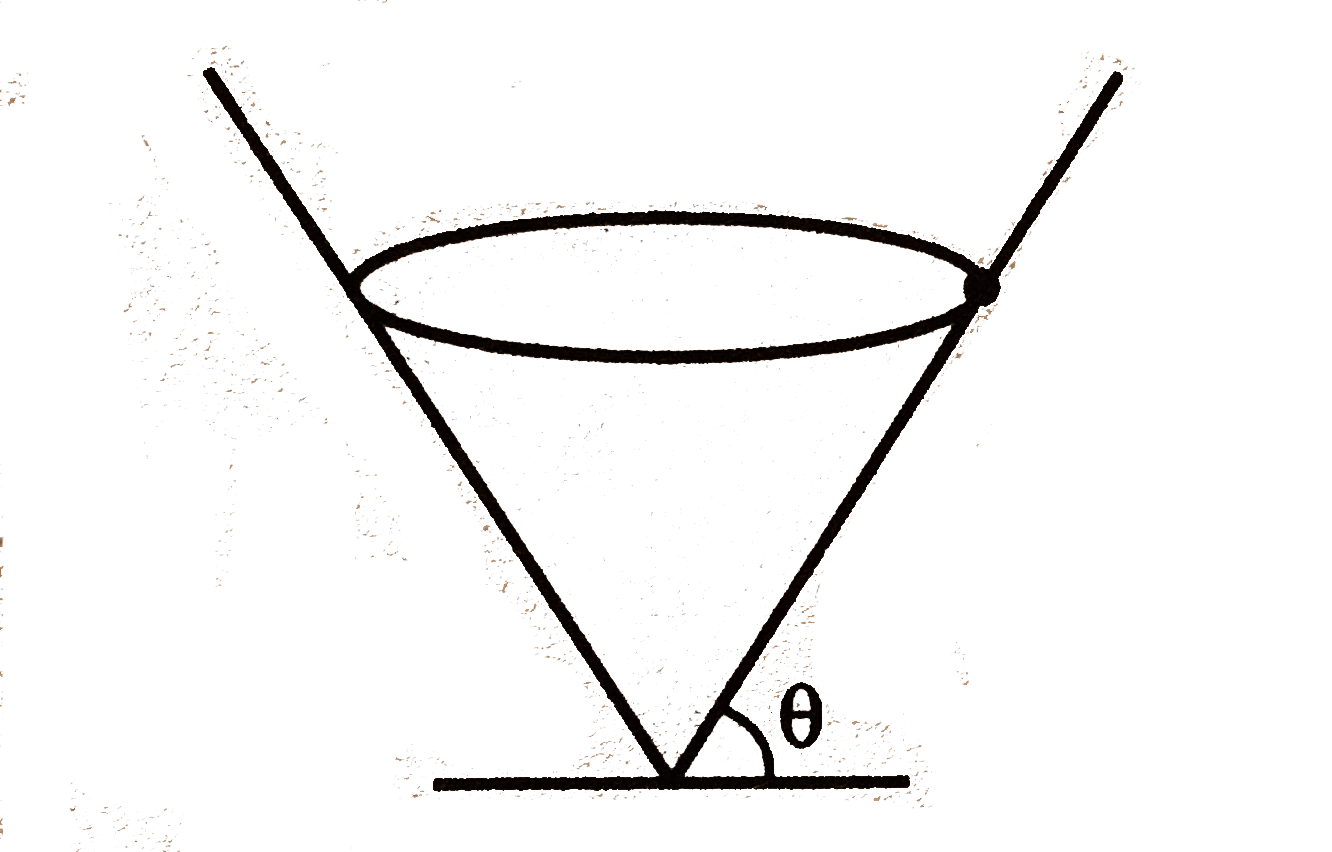
Reason: Acceleration of particle is not along the surface of funnel.
View SolutionAssertion: When water in a bucket is whirled fast overhead, the water does not fall out at the top of the ciorcular path.
Reason: The centripetal force in this position on water is more than the weight of water.
View SolutionTwo fixed frictionless inclined planes making angles 30° and 60° with the vertical are shows in the figure. Two blocks A and B are placed on the two planes. What is the relative vertical acceleration of A with respect to B ?
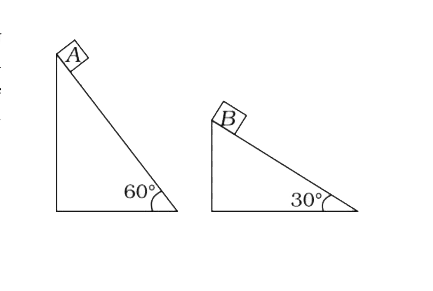
View SolutionOn a frictionless horizontal surface , assumed to be the ` x-y` plane , a small trolley `A` is moving along a straight line parallel to the `y-`axis ( see figure) with a constant velocity of `(sqrt(3)-1) m//s ` . At a particular instant , when the line `OA` makes an angle of `45(@)` with the `x -` axis , a ball is thrown along the surface from the origin `O`. Its velocity makes an angle `phi` with the `x -` axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle `theta` made by the velocity vector of the ball with the ` x-`axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ` phi = (4 theta )//(3)`.

View SolutionAssertion : A uniform circular motion is an accelerated motion.
Reason : Direction of acceleration is parallel to be velocity vector.
View SolutionAssertion In circular motion, dot product of v and `omega` is always zero.
Reason `omega` is always perpendicular to the plane of the circular motion.
View SolutionSTATEMENT -1 : In non - uniform circular motion acceleration of a particles is along the tangent of the circle .
STATEMENT -2 : In uniform circular motion acceleration of a particle is zero .
STATEMENT -3 : In no - uniform circular motion acceleration of a particle is towards the centre of the circle.
View SolutionAssertion In circular motion, average speed and average velocity are never equal.
Reason In any curvilinear path, these two are never equal.
View SolutionAssertion A particle is roting in a circle of radius 1 m. At some given instant, its speed is `2 ms^(-1)`. Then acceleration of particle at the given instant is `4 ms^(-2)`.
Reason Centripetal acceleration at this instant is `4 ms^(-2)` towards centre of circle.
View SolutionAssertion Centripetel force `(mv^(2))//(R)` acts on a particle rotating in a circle.
Reason Summation of net force acting on the particle is equal to `(mv^(2))//(R)` in the above case.
View SolutionAssertion If a particle is rotating in a circle, then centrifugal force is acting on the particle in radially outward direction .
Reason centrifugal force is equal and opposite to the centripetel force.
View SolutionAssertion When a car takes a circular turn on a horizontal road, then normal reaction on inner wheels is always less than the normal reaction on outer wheels.
Reason This is for rotational equilibrium of car.
View SolutionAssertion When water in a bucket is whirled fast overhead, the water does not fall out at the top of the circular path.
Reason The centripetel force in this position on water is more than the weight of water.
View SolutionAssertion In circular motion, average speed and average velocity are never equal.
Reason In any curvilinear path, these two are never equal.
View SolutionAssertion Angle `(theta)` between a and v in circular motion is
`0^(@)lt thetalt180^(@)`
Reason Angle between any two vectors lies in the above range.
View SolutionAssertion A ball tied by thread is undergoing circular motion (of radius R) in a vertical plane. (Thread always remains in vertical plane). The difference of maximum and minimum tension in thread is independent of speed (u) of ball at the lowest position `(ugtsqrt(5gR))`.
Reason For a ball of mass m tied by thread undergoing vertical circular motion (of radius R), difference in maximum and minimum magnitude of centripetal aceleraion of the ball is independent of speed (u) of ball at the lowest position `(ugrsqrt5gR))`.
View SolutionAssertion One end of a massless rod of length l is hinged so that it is free to rotate in vertical plane about a horizontal axis. If a particle is attached to the other end of the rod, then the minimum speed at lower most position of the particle is `sqrt(5gl)` to complete the circular motion.
Reason Work done by cnetripetal force on the particle is always zero.
View SolutionAssertion A car moves along a road with uniform speed. The path of car lies in vertical plane and shown in fighre. The radius of curvature (R) of the path is same everywhere. If the car does not loose contact with road at the highest point, it can travel the shown path without loosing contact with road anywhere else.
Reason For car to loose contact with road, the normal reaction between car and road should be zero.

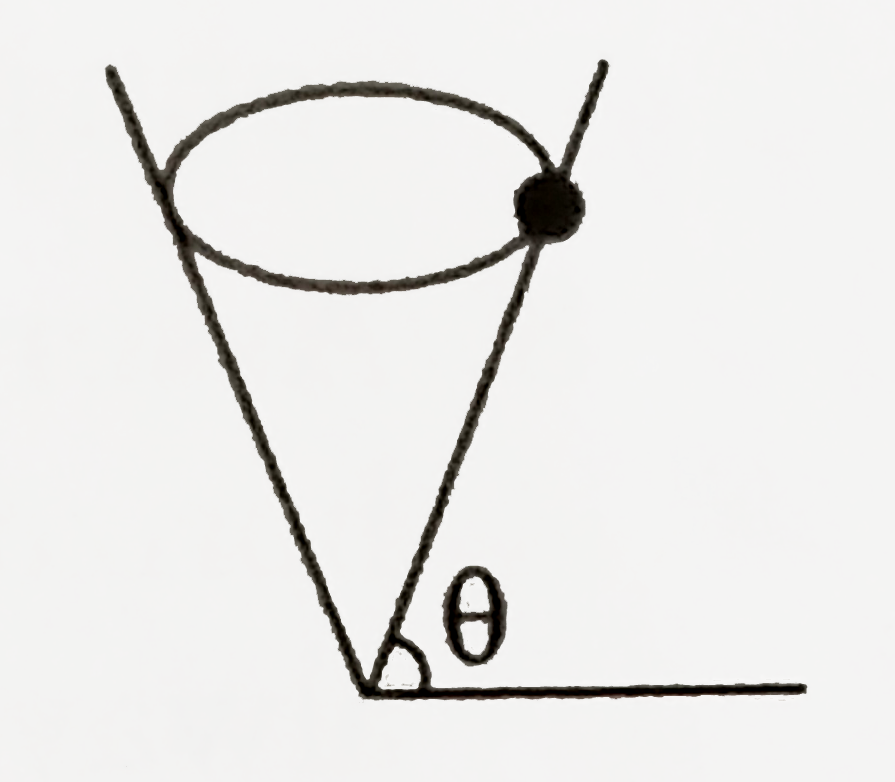
View SolutionAssertion A small block of mass m is rotating in a circle inside a smooth cone as shown in figure. In this case the normal reaction,
`N ne "mg cos"theta`
Reason In this case, acceleraion of the block is not along the surface of cone. It is horizontal.
View Solution
Assertion And Reason questions and complete solutions for chapter CIRCULAR MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS CIRCULAR MOTION
- Assertion And Reason
- Check point
- Comprehension
- Example
- Exercise 10.1
- Exercise 10.2
- Exercise 10.3
- Integer
- JEE Advanced
- JEE Main
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Matrix Matching
- Medical entrances s gallery
- Miscellaneous Examples
- More than One Option is Correct
- Solved Examples
- Subjective Questions
- Taking it together