Complete Solutions to Check point of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY NEET | Check point |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
If a flywheel makes `120" rev"//"min"`, then its angular speed will be
View SolutionThe ratio of angular speeds of minute hand and hour hand of a watch is
View SolutionThe wheel of a toy car rotates about a fixed axes. It slows down from 400 rps to 200 rps in 2 s. Then, its angular retardation in `"rad s"^(-2)` is (rps = revolutions per second)
View SolutionA rotating wheel changes angular speed from 1800 rpm to 3000 rpm in 20 s. What is the angular acceleration assuming to be uniform?
View SolutionA wheel is rotating at 900 rpm about its axis. When the power is cut off, it comes to rest in 1 min. The angular retardation (in rad `s^(-2)`) is
View SolutionThe motor of an engine is rotating about its axis with an angular velocity of 100 rpm. It comes to rest in 15 s after being switched off. Assuming constant angular deceleration, calculate the number of revolution made by it before coming to rest.
View SolutionIn case of a uniform circular motion, velocity and acceleration are
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA body is moving in a circular path with acceleration a. If its speed gets doubled, find the ratio of centripetal acceleration after and before the speed is changed
View SolutionThe circular orbit of two satellites have radii `r_(1)` and `r_(2)` respectively `(r_(1)ltr_(2))`. If angular velosities of satellites are same, then their centripetal accelerations are related as
View SolutionA particle is moving on a circular track of radius 30 cm with a constant speed of `6ms^(-1)`. Its acceleration is
View SolutionA particle moves along a circle of radius `(20/pi)` m with constant tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is : -
View SolutionIf `a_(r)` and `a_(t)` represent radial and tangential accelerations, the motion of a particle will be uniformly circular if
View SolutionA car has linear velocity v on a circular road of radius r. IF r it incrasing its speed at the rate of a `ms^(-2)`, then the resultant acceleration will be
View SolutionA point starts from rest and moves along a circular path with a constant tangential acceleration. After one rotation, the ratio of its radial acceleration to its tangential acceleration will be equal to
View SolutionA particle is moving on a circular path of 10 m radius. At any instant of time, its speed is `5m s^(-1)` and the speed is increasing at a rate of `2ms^(-2)` The magnitude of net acceleration at this instant is
View SolutionA body is moving on a circle of radius 80 m with a speed 20 m/s which is decreasing at the rate 5 `ms^(-2)` at an instant. The angle made by its acceleration with its velocity is
View SolutionA particle moves in a circular path of radius R with an angualr velocity `omega=a-bt`, where a and b are positive constants and t is time. The magnitude of the acceleration of the particle after time `(2a)/(b)` is
View Solutiona particle moves on a circular path of radius 8 m. distance traveled by the particle in time t is given by the equation `s=2/3 t^(3)`. Find its speed when tangential and normal accelerations have equal magnitude.
View SolutionA body is moving on a circle of radius 80 m with a speed 20 m/s which is decreasing at the rate 5 `ms^(-2)` at an instant. The angle made by its acceleration with its velocity is
View SolutionA particle of mass 2 kg is moving along a circular path of radius 1 m. If its angular speed is `2pi" rad s"^(-1)`, the centripetal force on it is
View SolutionTwo particles of equal masses are revolving in circular paths of radii `r_(1)` and `r_(2)` respectively with the same speed. The ratio of their centripetal force is
View SolutionA paticle of mass `m` is executing uniform circular motion on a path of radius `r`. If `p` is the magnitude of its linear momentum, then the radial force acting on the particle is
View SolutionA stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal circle. The maximum tension the string can withstand is 16 Newton . The maximum velocity of revolution that can be given to the stone without breaking it, will be
View SolutionIt mass, speed and radius of the circle of a particle moving uniformly in a circular path are all increased by `50%` , the necessary foce required to maintain the body moving in the circular path will have to be increased by
View SolutionA string of length `0.1` m cannot bear a tension more than 100 N. It is lied to a body of mass 100 g and rotated in a horizontal circle. The maximum angular velocity can be
View SolutionA mass 2 kg is whirled in a horizontal circle by means of a string at an initial speed of 5 revolutions per minute . Keeping the radius constant the tension in the string is doubled. The new speed is nearly
View SolutionA mass of 100 gm is tied to one end of a string 2 m long. The body is revolving in a horizontal circle making a maximum of 200 revolutions per min. The other end of the string is fixed at the centre of the circle of revolution. The maximum tension that the string can bear is (approximately)
View SolutionA car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is `mu`, the maximum velocity for no slipping is
View SolutionA car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A plumb bob is suspended from the roof of the car by a light rigid rod. The angle made by the rod with the vertical is `(g = 10 m//s^(2))`
View SolutionThe radius of the curved road on a national highway is `R`. The width of the road is `b`. The outer edge of the road is raised by `h` with respect to the inner edge so that a car with velocity `v` can pass safe over it. The value of `h` is
View SolutionA motor cyclist moving with a velocity of 72 km/hour on a flat road takes a turn on the road at a point where the radius of curvature of the road is 20 meters . The acceleration due to gravity is `10m//sec^(2)`. In order to avoid skidding, he must not bend with respect to the vertical plane by an angle greater than
View SolutionA car of mass `1000kg` negotiates a banked curve of radius `90m` on a frictionless road. If the banking angle is `45^(@)` the speed of the car is:
View SolutionKeeping the angle of banking, if the radius of curvature is made four times, the percentage increase in the maximum speed with which a vehicle can travel on a circular road is
View SolutionA person wants to drive on the vertical surface of a large cylindrical wooden 'well' commonly known as 'death well' in a circus. The radius of the well is R and the coefficient of friction between the tyres of the motorcycle and the wall of the well is u. The minimum speed the motor cyclist must have in order to prevent slipping should be -
View SolutionA motercyclist wants to drive on the vertical surface of wooden 'well' of radius 5 m, with a minimum speed of `5sqrt5ms^(-1)`. The minimum value of coefficient of friction between the tyres and the well must be (take, g = 10`ms^(-2)`)
View SolutionA block of mass m at the end of a string is whirled round in a vertical circle of radius R. The critical speed of the block at top of its swing below which the string would slacken before the block reaches the bottom is?
View SolutionA stone of mass of 1 kg is tied to the end of a string 1 m long. It is whirled in a vertical circle. The velocity of the stone at the bottom of the circle is just sufficient to take it to the top of circle without slackening of the string. What is the tension in the string at the top of the circle? (Take, g =10 `ms^(-2)`)
View SolutionA stone is attached to one end of a string and rotated in verticle cricle .If string breaks at the position of maximum tension, will break at
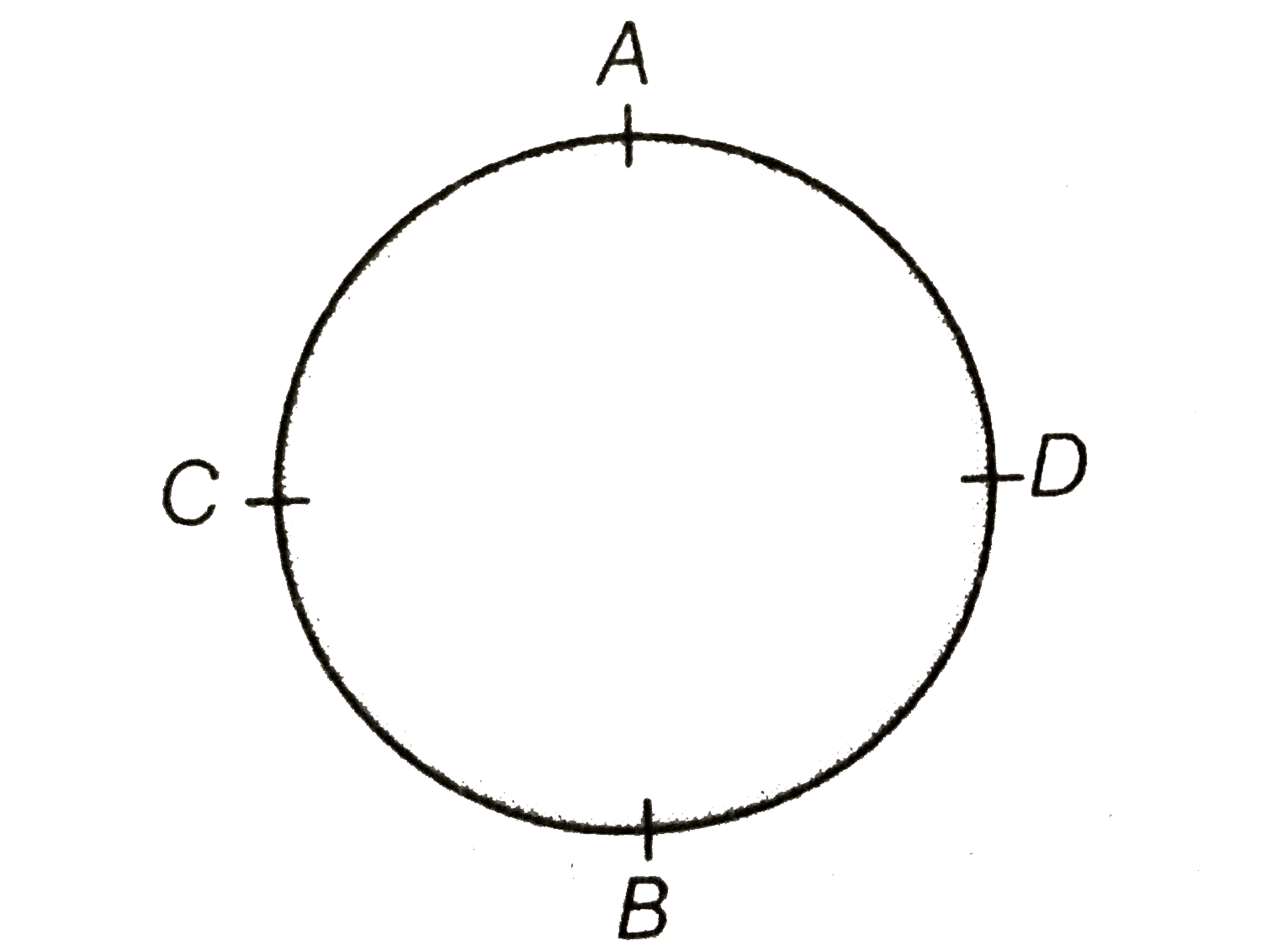
View SolutionA particle is moving in a vertical circle with constant speed. The tansions in the string when passing through two positions at angles `30^@` and `60^@` from vertical (lowest position) are `T_1` and `T_2` respectively. Then
View SolutionA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View SolutionAn isolated charge `q_(1)` of mass m is suspended freely by a thread of length l. Another charge `q_(2)` is brought near it `(rgtgtl)`. When `q_(1)` is in equilibrium tension in thread will be
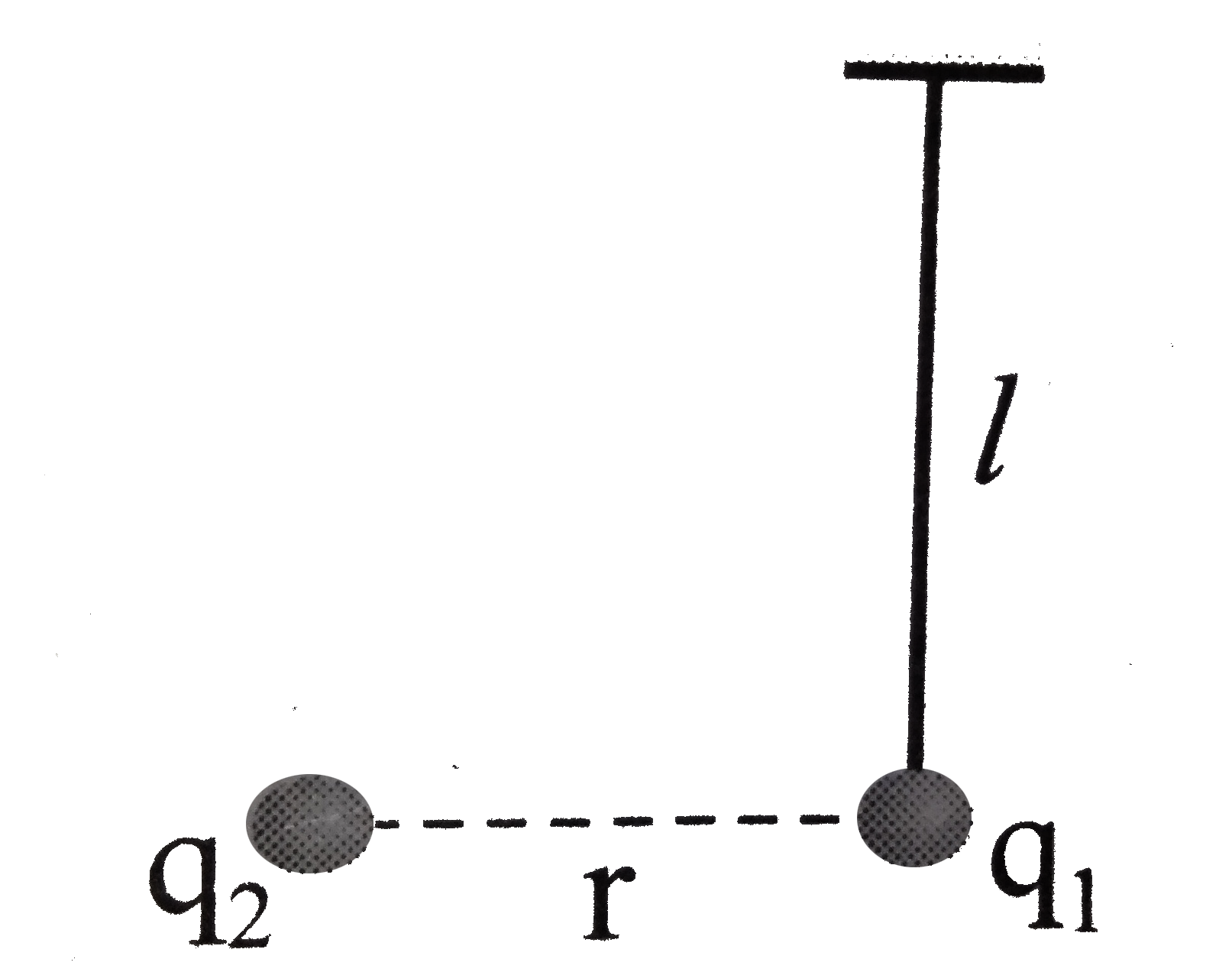
View SolutionA child is swinging a swing. Minimum and maximum heights fo swing from the earth's surface are 0.75 m and 2 m respectively. The maximum velocity of this swing is
View SolutionA national roadway bridge over a canal is in the form of an arc of a circle of radius 49 m. What is the maximum speed with which a car can move without leaving the ground at the highest point? (Take,`g=9.8ms^(-2)`)
View SolutionA frictionless track ABCDE ends in a circular loop of radius R. A body slides down the track from point A which is at height h = 5cm. Maximum value of R for a body to complete the loop successfully is
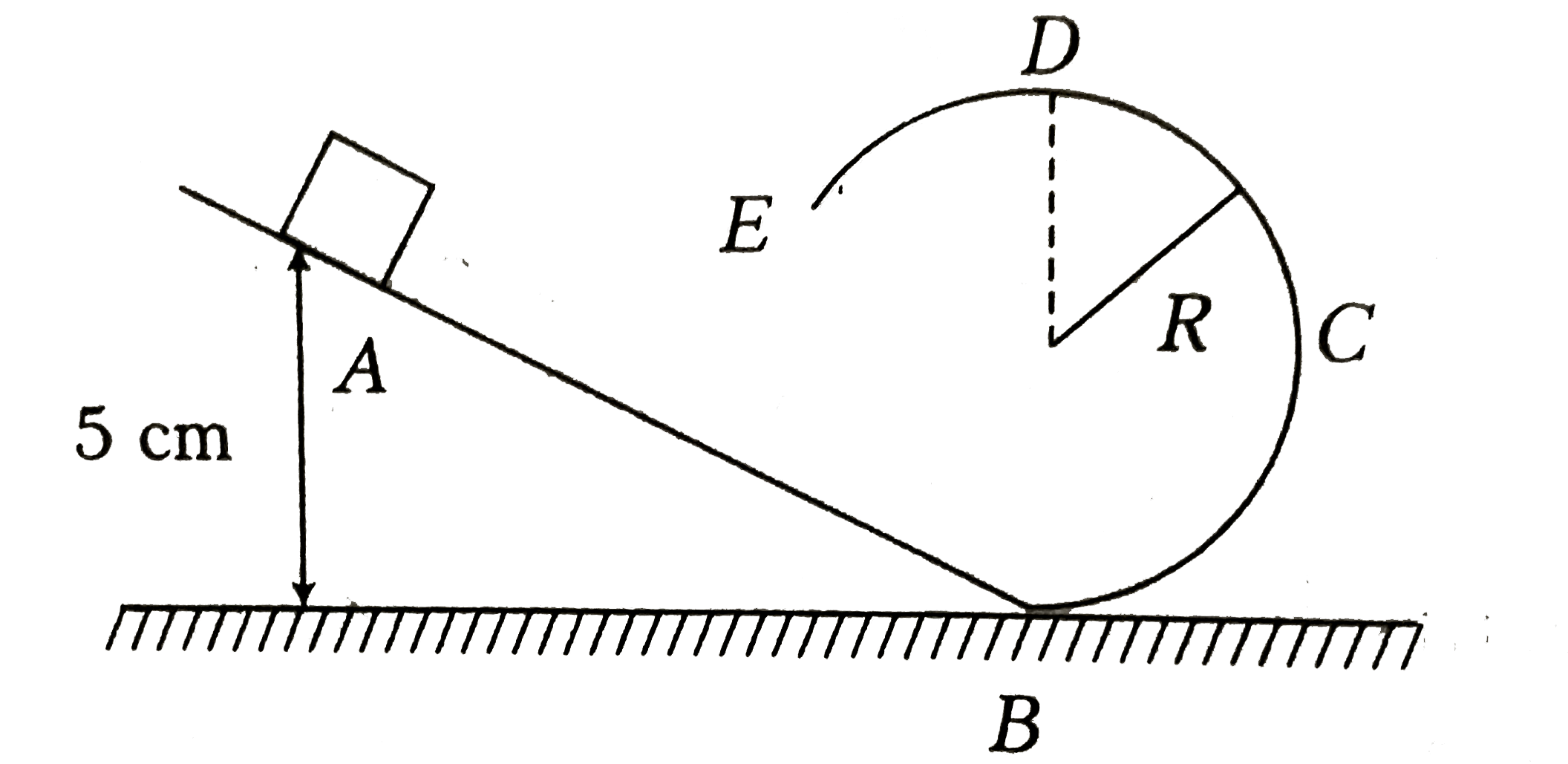
View Solution
Check point questions and complete solutions for chapter CIRCULAR MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY NEET Class 11 PHYSICS CIRCULAR MOTION
- Assertion And Reason
- Check point
- Comprehension
- Example
- Exercise 10.1
- Exercise 10.2
- Exercise 10.3
- Integer
- JEE Advanced
- JEE Main
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Matrix Matching
- Medical entrances s gallery
- Miscellaneous Examples
- More than One Option is Correct
- Solved Examples
- Subjective Questions
- Taking it together