Complete Solutions to Level 2 Subjective of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY | Level 2 Subjective |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
Bob `B` of the pendulum `AB` is given an initial velocity `sqrt(3Lg)` in horizontal direction. Final the maximum height of the bob from the starting point,
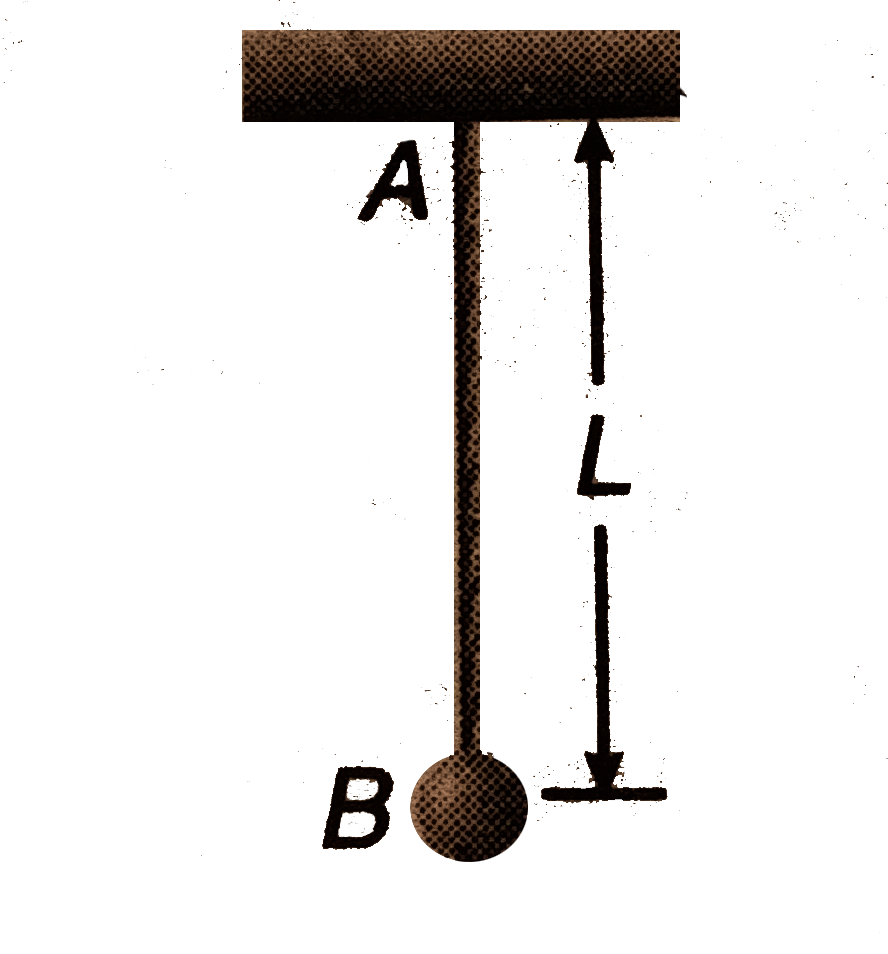
(a) if `AB` is a massless rod,
(b) if `AB` is a massless staring.
View SolutionA small sphere `B` of mass `m` is released form rest in the position shown and swings freely in a vertical plane, first about `O` and then about the peg `A` after the cord comes in contact with the peg. Determime the tension in the cord

(a) just before the sphere comes in contact with the peg.
(b) just after it comes in contact with the peg.
View SolutionA particle of mass `m` is suspended by a string of length `l` from a fixed rigid support. A sufficient horizontal velocity `=sqrt(3gl)` is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by `45^(@)` .
View SolutionA turn of radius 20 m is banked for the vehicles going at a speed of 36km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected by a speed u at an angle 'theta' with the horizontal, at a point where the particle velocity makes and angle `theta/2` with the horizontal?
View SolutionA particle is projected with velocity `20sqrt(2)m//s` at `45^(@)` with horizontal. After `1s` , find tangential and normal acceleration of the particle. Also, find radius of curvature of the trajectory at that point. (Take `g=10m//s^(2))`
View SolutionIf the system shown in the figure is rotated in a horizontal circle with angular velocity `omega` . Find `(g=10m//s^(2))`
(a) the minimum value of `omega` to start relative motion between the two blocks.
(b) tension in the string connecting `m_(1)` and `m_(2)` when slipping just starts between the blocks
The coefficient of frition between the two masses is `0.5` and there is no friction between `m_(2)` and ground. The dimensions of the masses can be neglected. (Take `R=0.5m,m_(1)=2Kg,m_(2)=1Kg)`

View SolutionThe simple `2Kg` pendulum is released from rest in the horizontal position. As it reaches the bottom position, the cord wraps around the smooth fixed pin at `B` and continues in the smaller arc in the vertical plane. Calculate the magnitude of the force `R` supported by the pin at `B` when the pendulum passes the position `theta=30^(@),(g=9.8m//s^(2))`
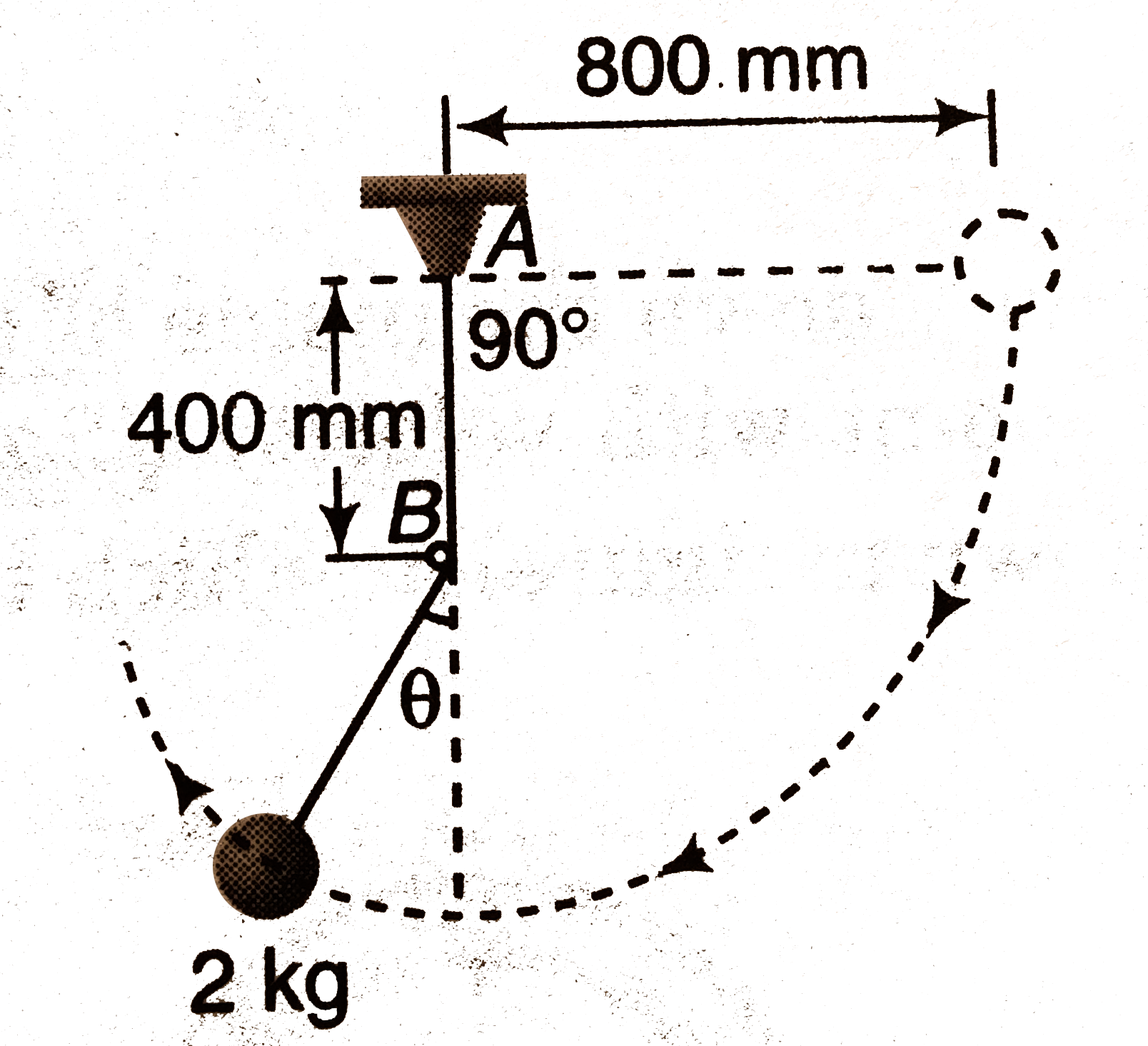
View SolutionA circular tube of mass `M` placed veticlly on a horizontal surface as shown in the figure. Two small spheres, each of mass `m` , just fit in the tube, are released from the top. If `theta` gives the angle between radius vector of eirther ball with the vertical, obtain the value of the ratio `M//m` if the tube breacks its contact with ground when `theta=60^(@)` . Neglect any friction.

View SolutionA table with smooth horizontal surface is turning at an angular speed `omega` about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from the centre becomes L.
View SolutionA block of mass `m` slides 0n a frictionless table. It is constrained to move inside a ring of radius `R` . At time `t=0` , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity `v_(0)` . The coefficient of friction between the block and the ring is `mu` . Find the speed of the block at time `t` .

View SolutionA ring of mass `M` hangs from a thread and two beads of mass `m` slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if `mgt(3M)/(2)`
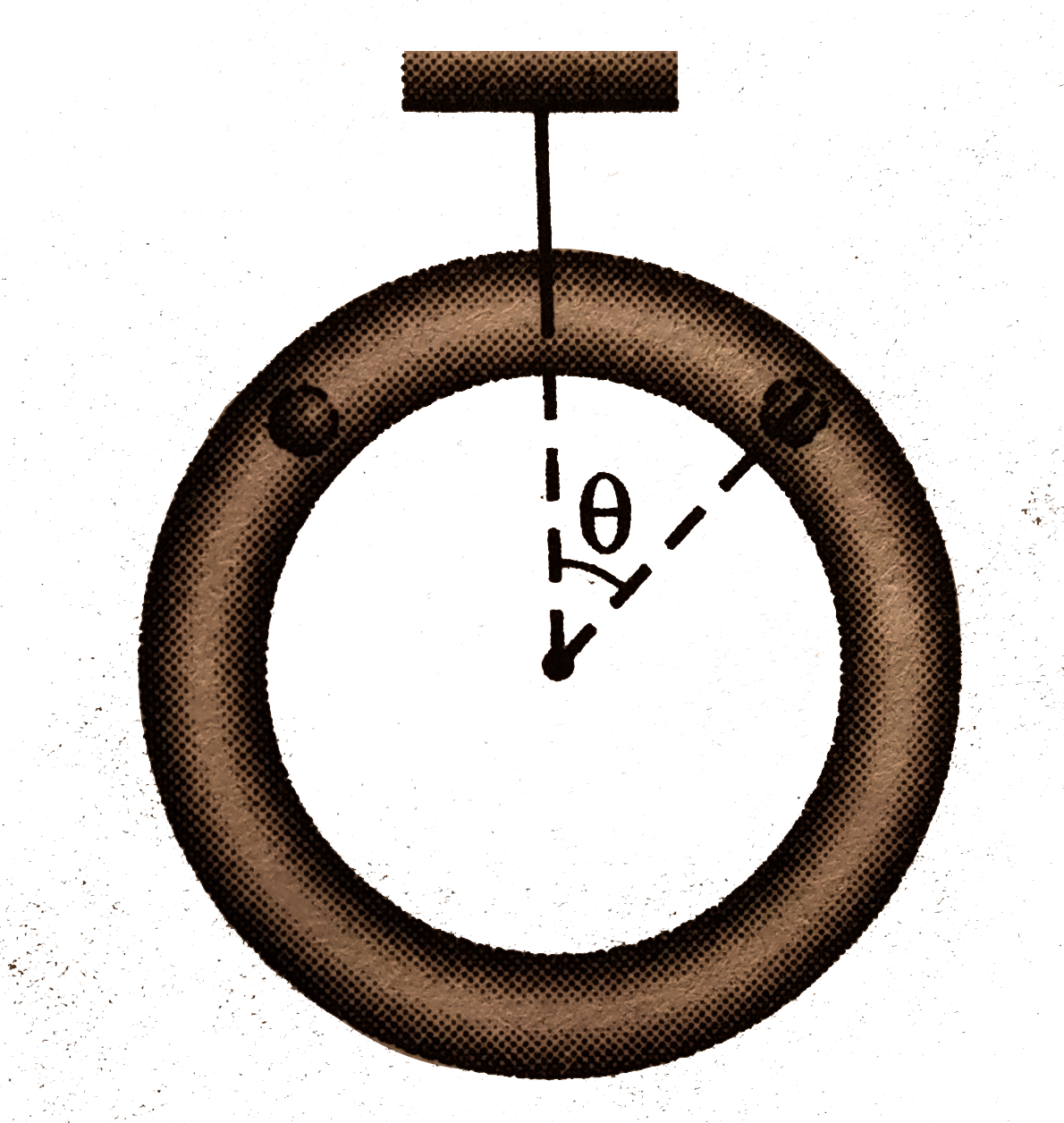
View SolutionA smooth circular tube of radius `R` is fixed in a vertical plane. A particle is projectid from its lowest point with a velocity just sufficient to carry it to th ehigest point. Show that the time taken by the particle to rach the end of the horizontal diameter is `(sqrt(R)/(g))In(1+sqrt(2))` .
Hint : `intsectheta.dtheta=In(sectheta+tantheta)`
View Solution
Level 2 Subjective questions and complete solutions for chapter CIRCULAR MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS CIRCULAR MOTION
- Assertion And Reason
- Check point
- Comprehension
- Example
- Exercise 10.1
- Exercise 10.2
- Exercise 10.3
- Integer
- JEE Advanced
- JEE Main
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Matrix Matching
- Medical entrances s gallery
- Miscellaneous Examples
- More than One Option is Correct
- Solved Examples
- Subjective Questions
- Taking it together