Complete Solutions to Level 1 Objective of chapter WORK, ENERGY & POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY & POWER |
| DC PANDEY | Level 1 Objective |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
Identify, which of th following energies can be positive (or zero) only ?
View SolutionThe total work done on a particle is equal to the change in its kinetic energy
View SolutionWork done by force of static friction .
View SolutionWork done when a force `F=(hati + 2hat(j) + 3hatk) N` acting on a particle takes it from the point
`r_(1) =(hati + hatk)` the point `r_(2) =(hati -hatj + 2hatk)` is .
View SolutionA particle moves along the x-axis from `x=0` to `x=5m` under the influence of a given by `F =7-2x + 3x^(2)`. The work done by the applied force to the particle is.
View SolutionA particle moves with a velocity `v=(5hati-3hatj + 6hatk) ms^(-1)` under the influence of a constant force
`F =(10hati + 10hatj + 20hath) N`, the instantaneous power applied to the particle is.
View SolutionA pump is required to lift `800 kg` of water per minute from a 10 m deep well and eject it with speed of `20 kg m//s` . The required power in watts of the pump will be
View SolutionA ball is dropped onto a floor from a height of `10 m`. If `20%` of its initial energy is lost,then the height of bounce is
View SolutionA body with mass `1kg` moves in one direction in the presence of a force which is described by the potential energy graph. If the body is releasd from rest at `x=2 m`, than its speed when it crosses `x=5 m`, is (Neglect dissipative forces).
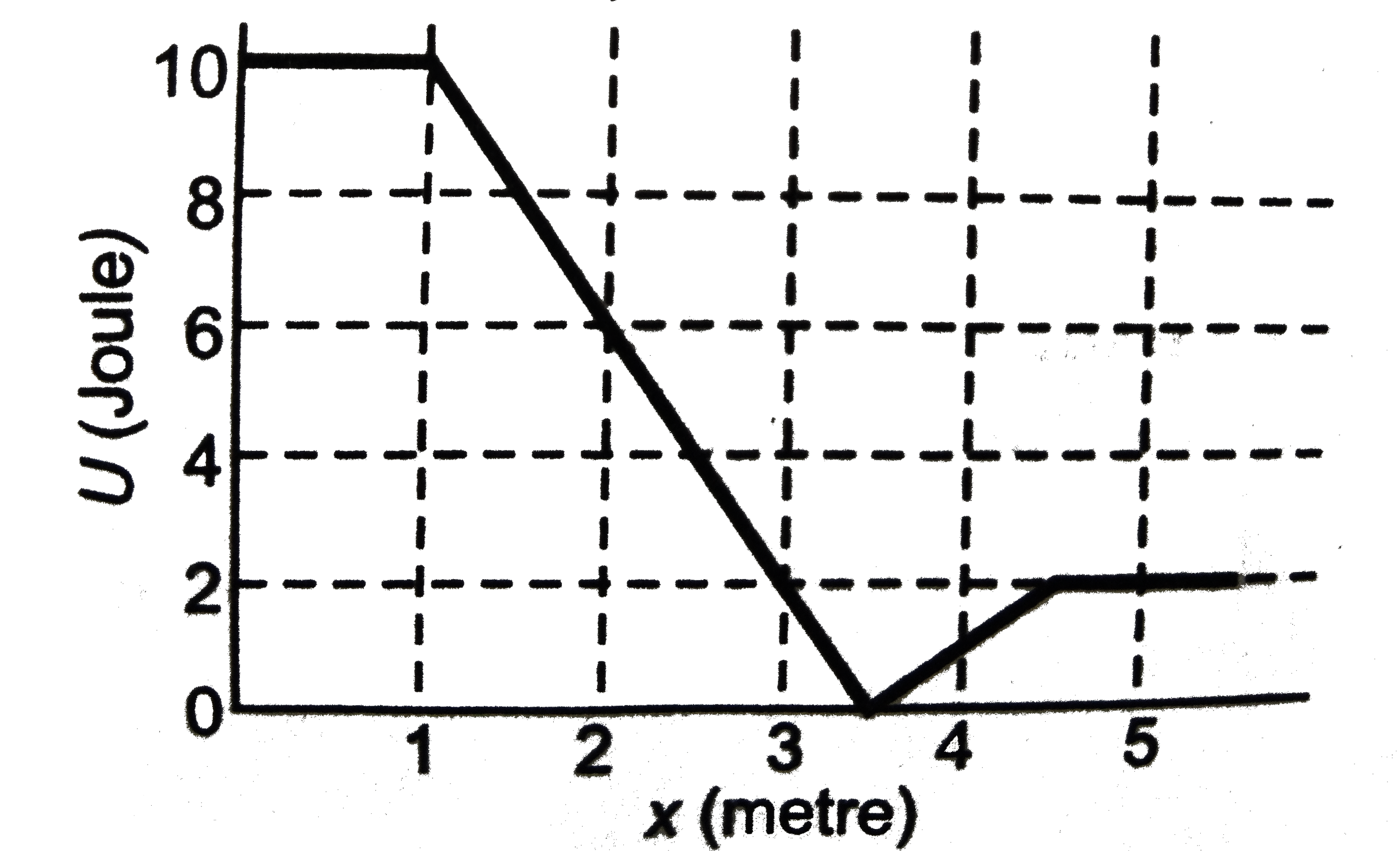
View SolutionA body has kinetic energy E when projected at angle of projection for maximum range. Its kinetic energy at the highest point of its path will be
View SolutionA person pulls a bucket of water from a well of depth h. if the mass of uniform rope is and that of the bucket full 0f water is M, then work done by the person is.
View SolutionThe velocity of a particle decreases uniformly from `20 ms^(-1)` to zero in to `10 s` as shown in figure. If the mass of the particle is `2 kg`, the identify the correct statement.
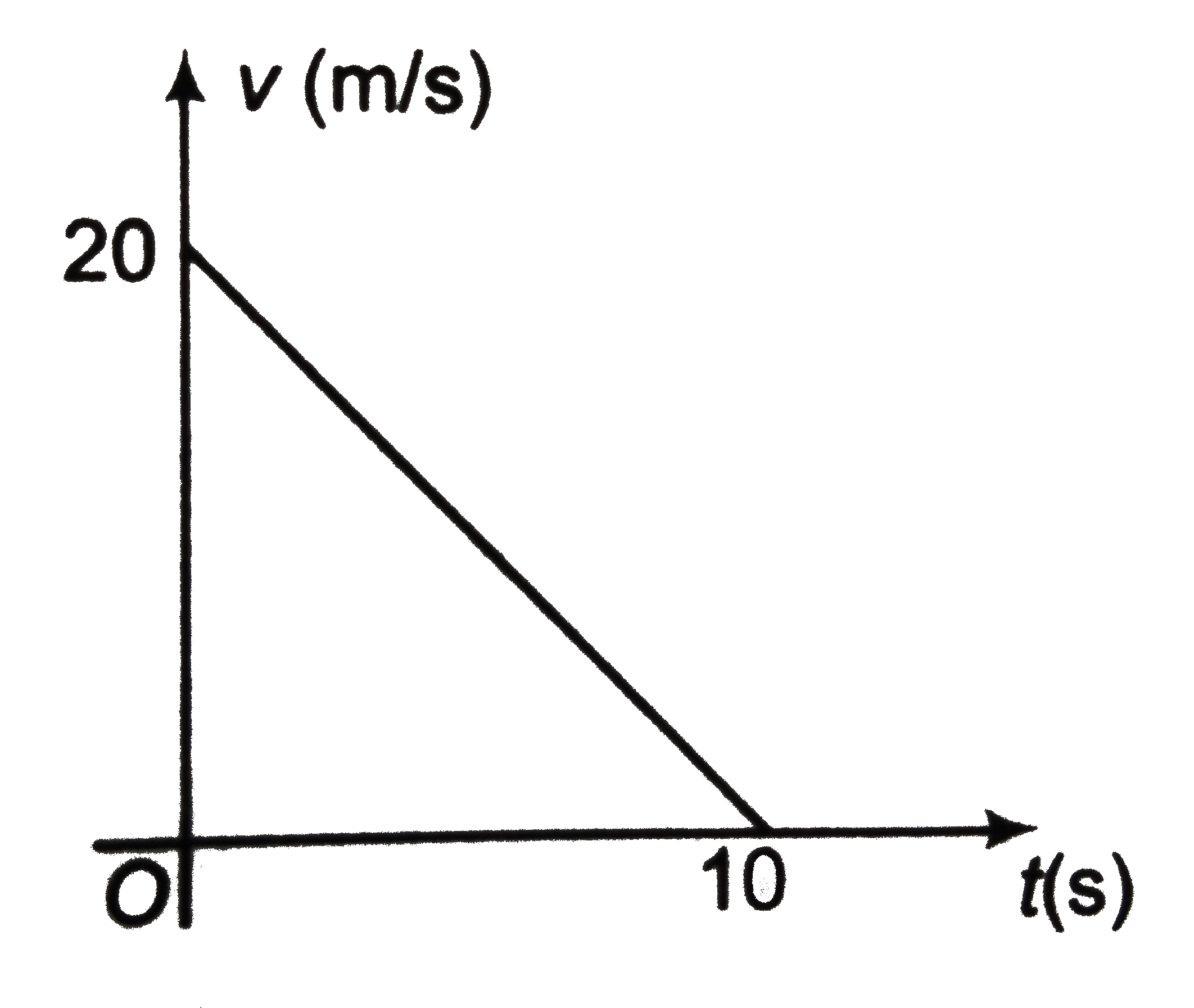 .
.
View SolutionThe minimum stopping distance of a car moving with velocity `u` is `x`. If the car is moving with velocity 2v, then the minimum stopping distance will be.
View SolutionA projectile is fired from the origin with a velocity `v_(0)` at an angle `theta` with x-axis. The speed of the projectile at an altitude `h` is .
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA body moves under the action of a constant force along a straight line. The instantaneous power developed by this force with time `t` is correctly represented by.
View SolutionA ball is dropped at `t=0` from a height on a elastic surface. Identify the gragh which correctly represents relation of kinetic energy K with time t.
View SolutionA block of mass 5 kg is raised from the bottom of the lake to a height of 3m without change in kinetic energy. If the density of the block is `3000 kg m^(-3)`, then the work done is equal to.
View SolutionA bode mass m is projected at an angle `theta` with the horizontal with an initial velocity u, the average power of gravitational force over the whole time of flight is.
View SolutionA spring of force constant k is cut in two parts at its one-third lingth. When both the parts are stretched by same amount. The word done in the two parts will be .
View SolutionA particle moves under the action of a force `F=20hati + 15hatj` along a straight line `3y + alphax =5`, where, `alpha` is a constant. If the work done by the force F is zero the value of `alpha` is .
View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View SolutionA force`F=(3thati + 5hatj)N` acts on a body due to which its displacement varies as `S=(2t^(2)hat-5hatj)m`. Work done by these force in `2 s` is .
View SolutionAn open knife of mass m is dropped from a height h on a wooden floor. If the blade penetrates up to the depth d into the wood. The average resistance offered by the wood to the knife edge is to the depth d into the wood, the average resistance offered by the wood to the knife edge is .
View SolutionTwo springs have force constants `k_(A)` such that `k_(B)=2k_(A)`. The four ends of the springs are stretched by the same force. If energy stored in spring `A` is `E`, then energy stored in spring `B` is
View SolutionA mass of `0.5 kg` moving with a speed of `1.5 m//s` on a horizontal smooth surface, collides with a nearly weightless spring of force constant `k =50 N//m` The maximum compression of the spring would be.
View SolutionA bullet moving with a speed of `100 ms^(-1)` can just penetrate into two planks of equal thickness. Then the number of such planks, if speed is doubled will be .
View SolutionA body of mass 100 g is attached to a hanging spring force constant is `10 N//m`. The body is lifted until the spring is in its unstretched state and then released. Calculate the speed of the body when it strikes the table `15 cm` below the release point .
View SolutionAn ideal massless spring S can compressed `1.0` m in equilibrium by a force of `1000 N`. This same spring is placed at the bottom of a friction less inclined plane which makes an angle `theta =30^@` with the horizontal. A `10 kg` mass `m` is released from the rest at top of the inclined plane and is brought to rest momentarily after compressing the spring by `2.0 m.` the distance through which the mass moved before coming to rest is.
View SolutionA body of mass m is released from a height h on a smooth inclined plane that is shown in the figure. The following can be true about the velocity of the block knowing that the wedge is fixed.
 .
.
View SolutionA block of mass m is directly pulled up slowly on a smooth inclined plane of height h and inclination `theta` with the help of a string parallel to the incline. Which of the following statement is incorrect for the block when it moves up from the bottom to the top the incline? .
 .
.
View SolutionA spring of natural length `l` is compressed vertically downward against the floor so that its compressed lengtg becomes `(1)/(2)`. On releasing, the spring attins its natural length. If `k` is the siffness constant of spring, then the work done by the spring on the floor is
View SolutionThe relationship between the force F and position x of body is as shown in figure. The work done in displacing the body in displacing the body from (`x = 1 m` to `x = 5 m`) will be
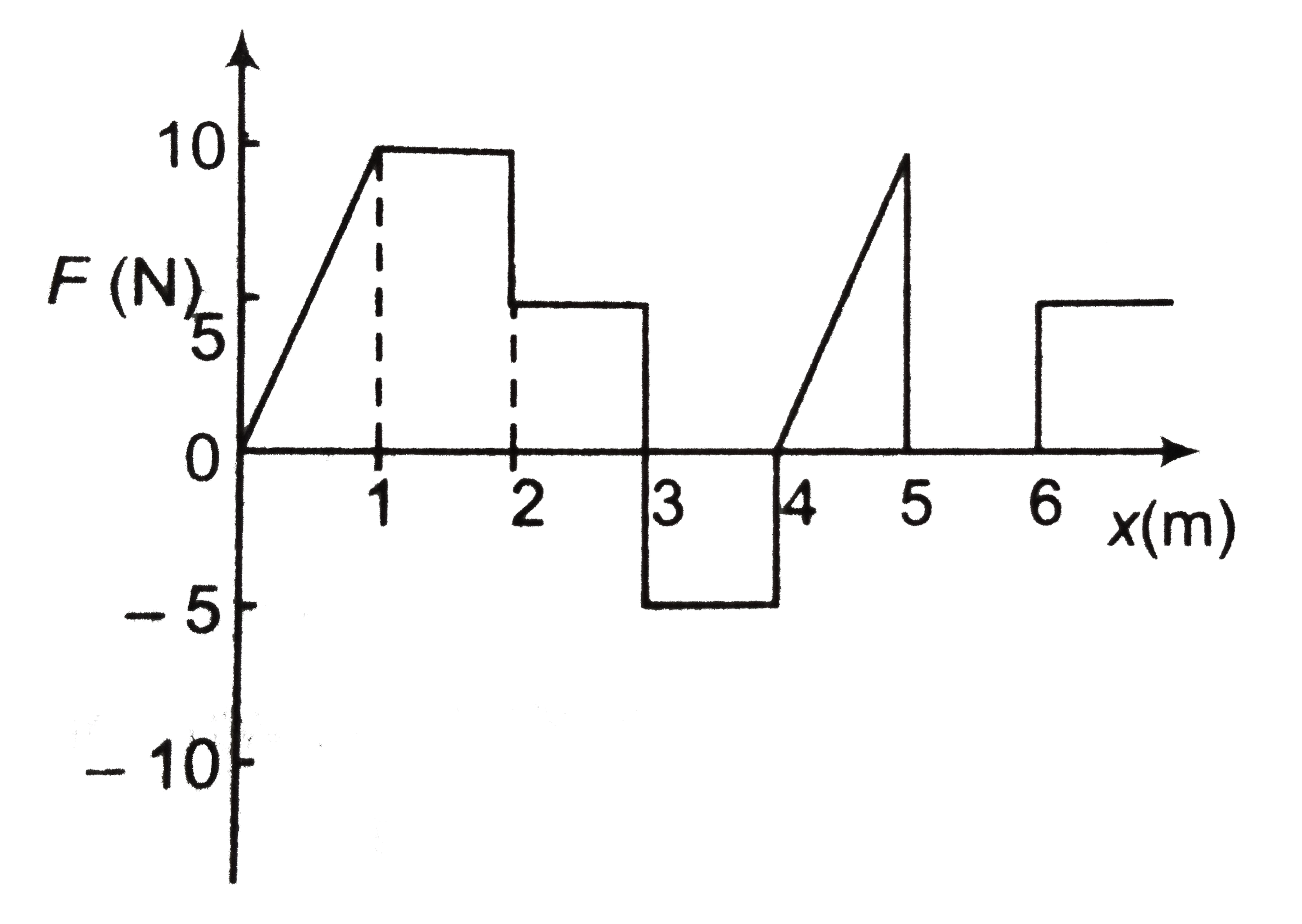 .
.
View SolutionUnder the action of a force, a `2 kg` body moves such that its position x as a function of time is given by `x =(t^(3))/(3)` where x is in meter and t in second. The work done by the force in the first two seconds is .
View SolutionThe kinetic energy of a projectile at its highest position is `K`. If the range of the projectile is four times the height of the projectile, then the initial kinetic energy of the projectile is .
View SolutionPower applied to a particle varices with time as `P =(3t^(2)-2t + 1)` watt, where t is in second. Find the change in its kinetic energy between time `t=2s` and `t = 4 s` .
View SolutionA bolck of mass `10 kg` is moving in x-direction with a constant speed of `10 m//s`. it is subjected to a retardeng force `F=-0.1 x J//m`. During its travel from `x =20m` to `x =30 m`. Its final kinetic energy will be .
View SolutionA ball of mass `12 kg` and another of mass `6 kg` are dropped from a `60` feet tall building after a fall of `30` feet each, towards earth, their kinetic energies will be in the ratio of .
View Solution
Level 1 Objective questions and complete solutions for chapter WORK, ENERGY & POWER of DC PANDEY ENGLISH of Class 11