Complete Solutions to (A) Taking it together of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| DC PANDEY NEET | (A) Taking it together |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
A bo walks to his school at a distance of 6 km with constant speed of `2.5 kmh^(-1)` and walks back with a constant speed of `4 kmh^(-1)`. His average speed for round trip expressed in `kmh^(-1)`, is
01:41View SolutionA man walks on a straight road form his home to a market 2.5 km away with speed of 5 `(km)/(hr)`. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 `(km)/(hr)`. The average speed of the man over the intervel of time 0 to 40 min is equal to
02:41View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration `(4)/(3) ms^-2`, in the third second is.
01:42View SolutionA particle moves in a straight line with a constant acceleration. It passing through a distance 135 m in t second. The value of t (in second) is
View SolutionA particle moves along x-axis as `x=4(t-2)+a(t-2)^2`
Which of the following is true?03:18View SolutionA car moving with a velocity of 10m/s can be stopped by the application of a constant force F In a distance of 20m. If the velocity of the car is 30m/s. It can be stopped by this force in
01:40View SolutionA vehicle travels half the distance (L) with speed ` V_1` and the other half with speed ` V_2`, then its average speed is .
02:00View SolutionThe x and y coordinates of a particle at any time t are given by `x=7t+4t^2` and `y=5t`, where x and t is seconds. The acceleration of particle at `t=5`s is
02:14View SolutionA body `A` starts from rest with an acceleration `a_1`. After `2` seconds, another body `B` starts from rest with an acceleration `a_2`. If they travel equal distances in the `5th` second, after the start of `A`, then the ratio `a_1 : a_2` is equal to :
03:09View SolutionFigure given shows the distance - time graph of the motion of a car. It follows from the graph that the car is
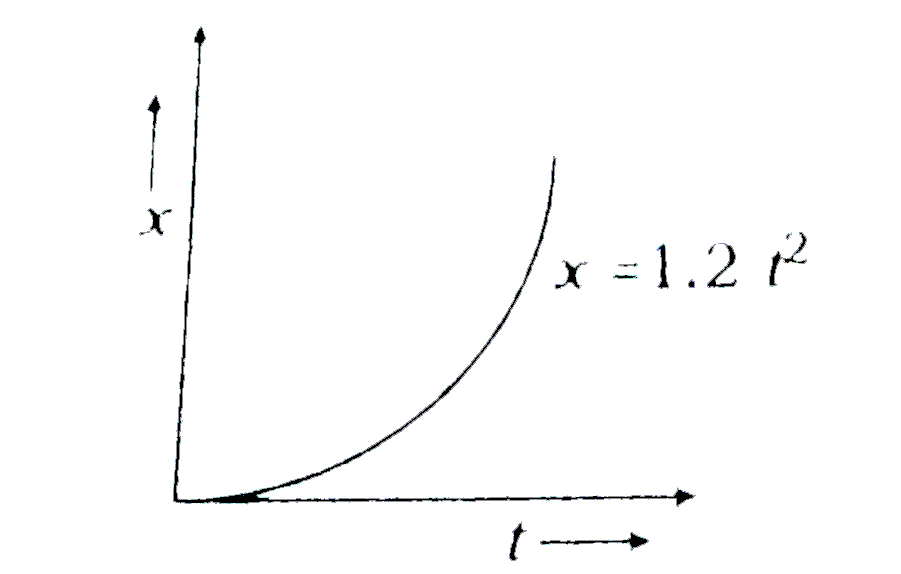 01:34View Solution
01:34View SolutionWhich of the following speed - time `(upsilon-t)` graph is physically not possible ?
02:04View SolutionThe displacement (x)-time (t) graph of a particle is shown in figure. Which of the following is correct ?
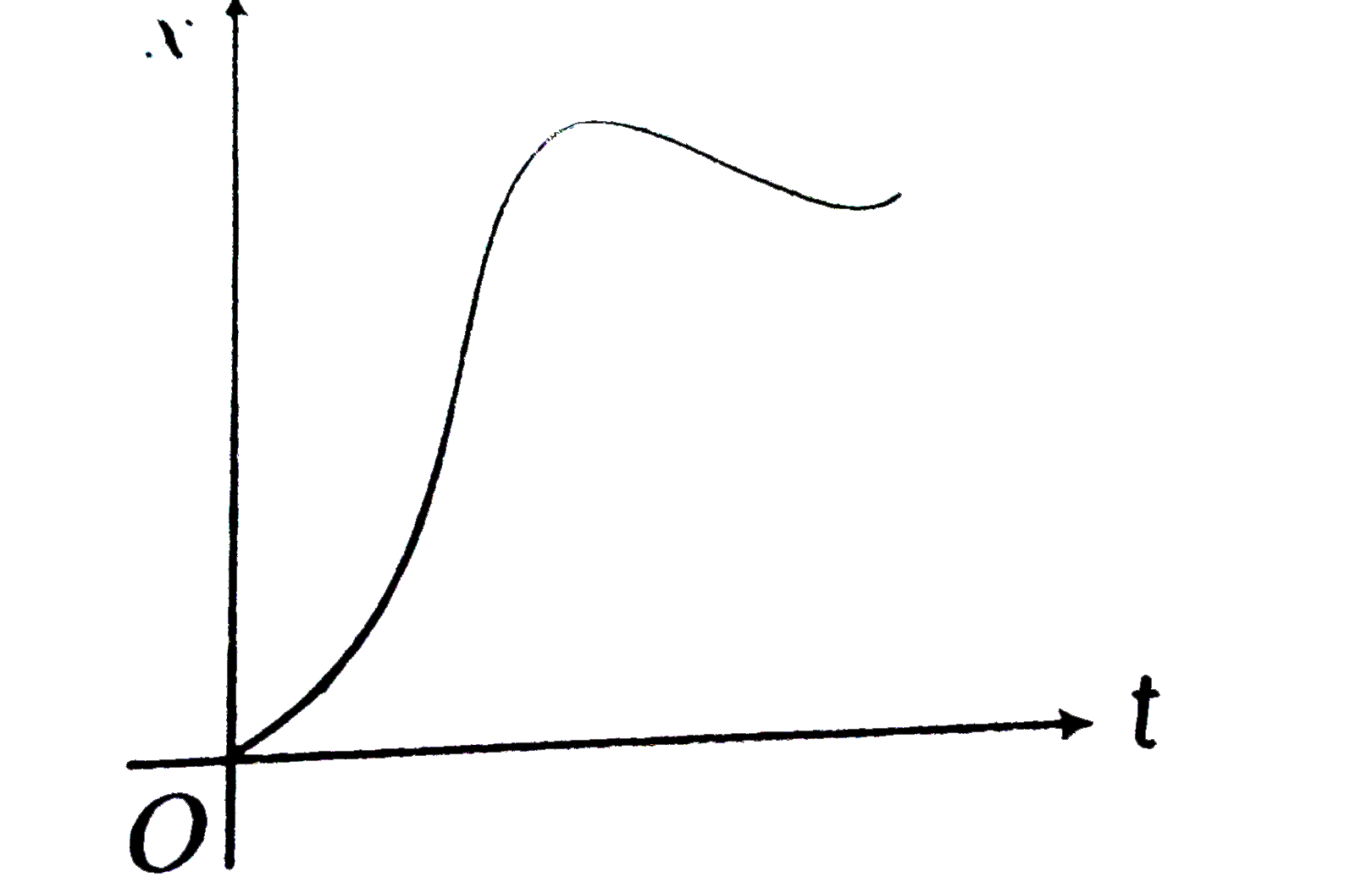 02:49View Solution
02:49View SolutionThe velocity fo a body depends on time according to equation, ` v= 2.0 + 0.1 t^2`. The body is undergoing.
02:24View SolutionA particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point.
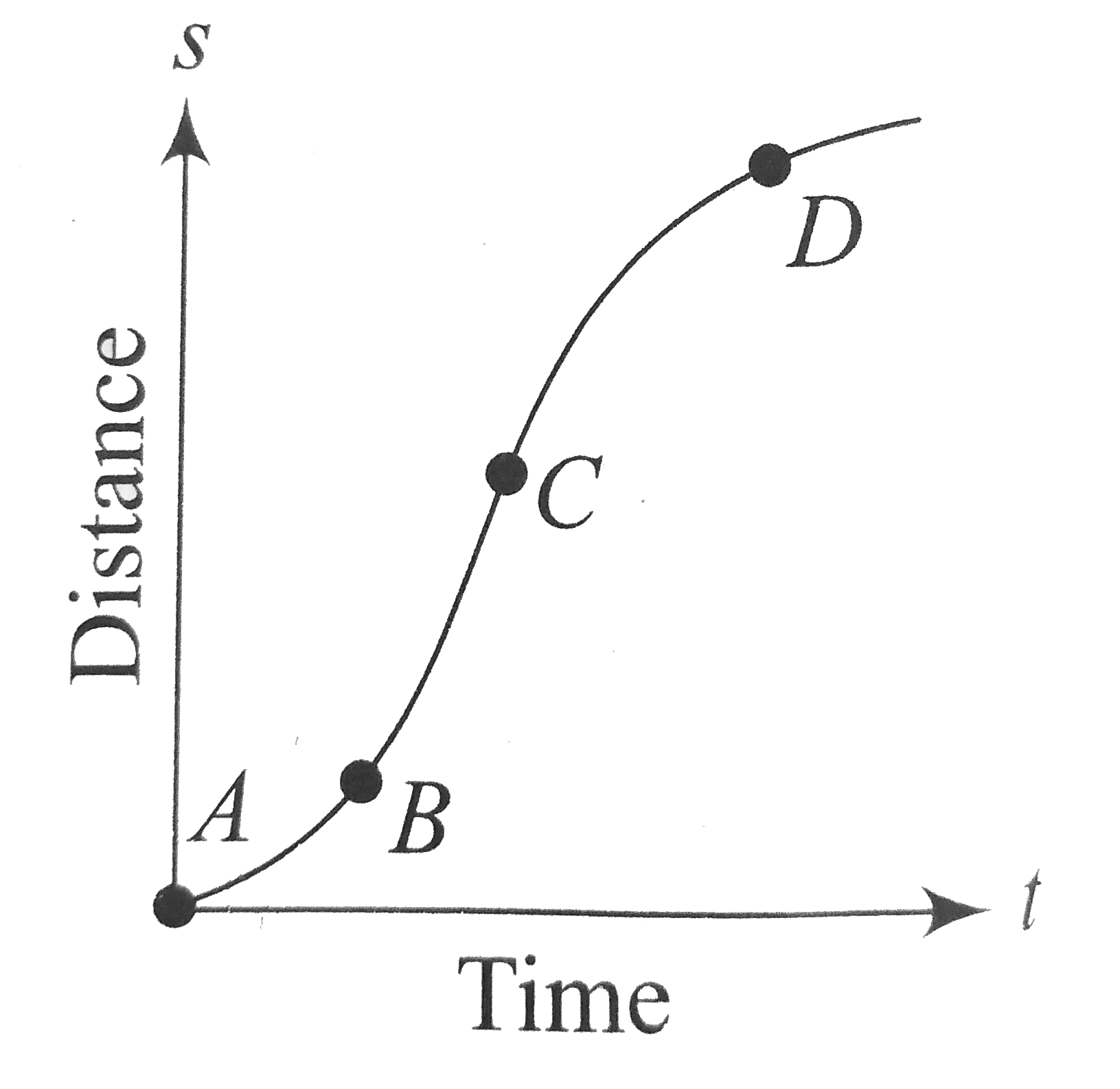 .02:12View Solution
.02:12View SolutionThe displacement-time graph of moving particle is shown below

The instantaneous velocity of the particle in negative at the point02:26View SolutionThe velocity `upsilon` of a particle as a function of its position (x) is expressed as `upsilon = sqrt(c_(1)-c_(2)x)`, where `c_(1)` and `c_(2)` are positive constants. The acceleration of the particle is
01:34View SolutionA person walks up a stalled escalator in 90 s. When standingon the same escalator, now moving, he is carried in 60 s.The time it would take him to walk up the moving escalator will be:
02:39View SolutionA car starts moving along a line, first with acceleration a=5 `ms^(-2)` starting from rest then uniformly and finally decelerating at the same rate a, comes to rest.The total time of motion is `tau=25 s`. The average velocity during the time is equal to lt v gt =72 km/hr.How long does the partial move uniformly ?
03:48View SolutionThe displacement (x) of a particle depends on time t as `x=alpha t^(2)-beta t^(3)`. Choose the incorrect statements from the following.
04:01View SolutionA starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to `t=t_(1)` will be
02:58View SolutionA ball is dropped onto the floor from a height of 10 m. It rebounds to a height of 5 m. If the ball was in contact with the floor for `0.01 s`, what was its average acceleration during contact ? (Take `g=10 ms^(-2)`)
03:24View SolutionParticle A is moving along X-axis. At time t = 0, it has velocity of `10 ms^(-1)` and acceleration `-4ms^(-2)`. Particle B has velocity of `20 ms^(-1)` and acceleration `-2 ms^(-2)`. Initially both the particles are at origion. At time t = 2 distance between the particles are at origin. At time t = 2 s distance between the particles is
02:58View SolutionAt a metro station, a girl walks up a stationary escalator in time `t_1` If she remains stationary on the escalator, then the escalator take her up in time `t_2`. The time taken by her to walk up the moving escalator will be.
03:16View SolutionThe displacement of a body along X-axis depends on time as `sqrt(x)=t+1`. Then the velocity of body.
01:28View SolutionA cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ circumference and returns to the centre along OQ as shown in fig. If the round trip taken ten minute, the net displacement and average speed of the cyclist (in kilometer and kilometer per hour) is
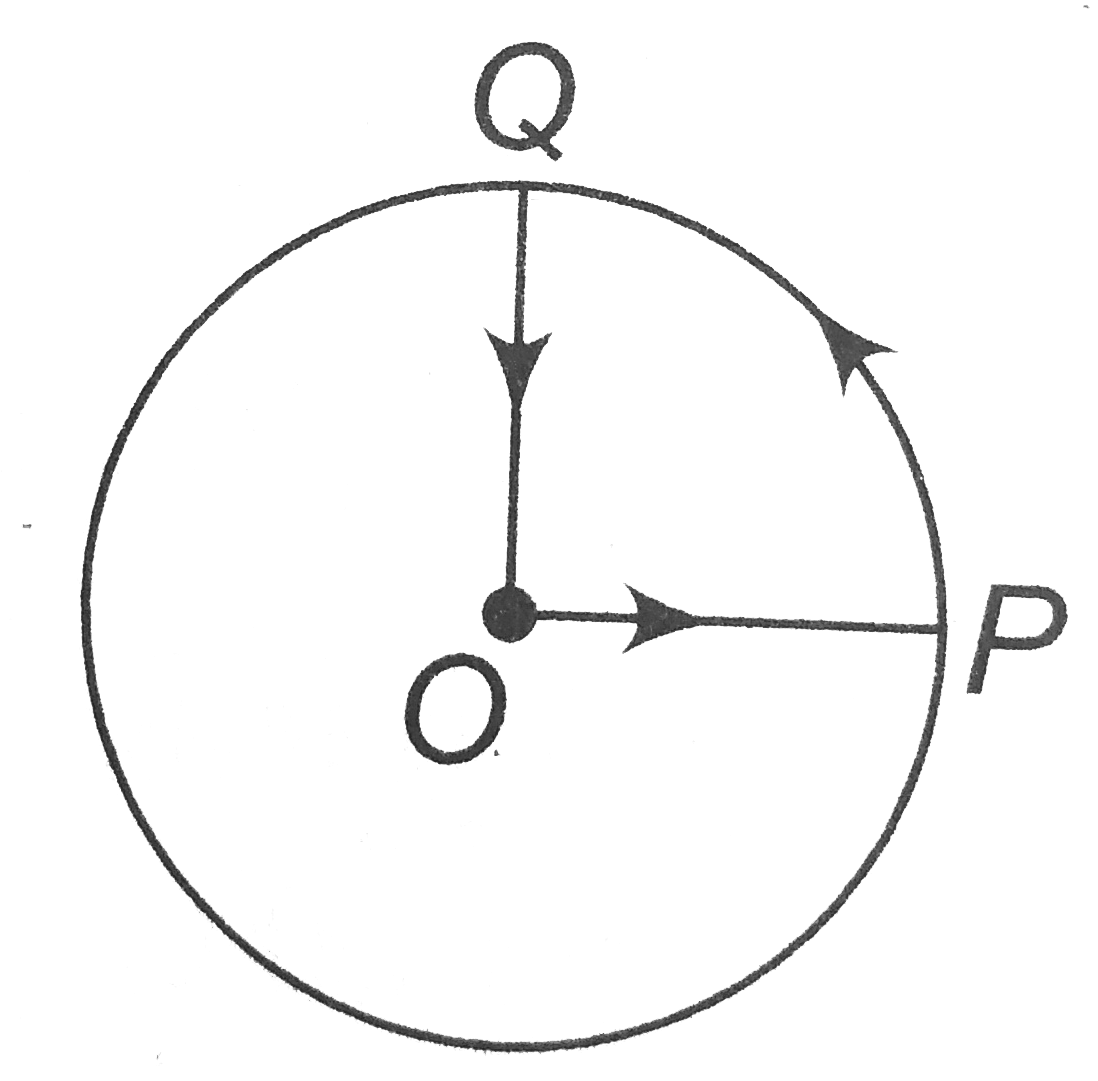 07:52View Solution
07:52View SolutionA particle moves along a straight line `OX`. At a time `t` (in seconds) the distance `x` (in metre) of the particle is given by `x = 40 +12 t - t^3`. How long would the particle travel before coming to rest ?
01:50View SolutionTwo boys are standing at the ends A and B of a ground, where `AB=a`. The boy at B starts running in a direction perpendicular to AB with velocity `v_(1)`. The boy at A starts running simultaneously with velocity v and catches the other boy in a time t, where t is :
02:48View SolutionA bullet emerges from a barrel of length `1.2 m` with a speed of `640 ms^(1)`. Assuming constant acceleration, after the gun is fired is
02:27View SolutionFrom the top of a tower, 80m high from the ground a stone is thrown in the horizontal direction with a velocity of `8 ms^(1)`. The stone reaches the ground after a time t and falls at a distance of d from the foot of the tower. Assuming `g=10ms^(2)`, the time t and distance d are given respectively by
02:42View SolutionA boggy of uniformly moving train is suddenly detached from train and stops after covering some distance. The distance covered by the boggy and distance covered by the train in the same time has relation
04:27View SolutionA man is 45 m behind the bus when the bus starts acceleration from rest with acceleration `2.5(m)/(s^2)`. With what minimum velocity should man start running to catch the bus?
03:23View SolutionA body moves for a total of nine second starting from rest with uniform acceleration and then with uniform retardation, which is twice the value of acceleration and then stop. The duration of uniform acceleration is
04:13View SolutionA point initially at rest moves along x-axis. Its acceleration varies with time as `a = (6t + 5) m//s^(2)`. If it starts from origin, the distance covered in 2 s is:
02:26View SolutionThe time taken by a block of wood (initially at rest) to slide down a smooth inclined plane 9.8 m long (angle of inclination is `30^(@)`) is
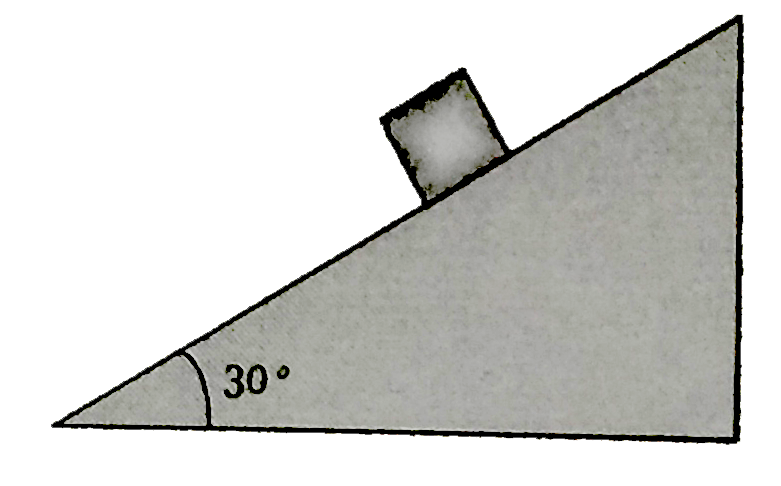 01:27View Solution
01:27View SolutionA particle move a distance `x` in time `t` according to equation `x = (t + 5)^-1`. The acceleration of particle is alphaortional to.
02:26View SolutionA ball is thrown straight upward with a speed v from a point h meter above the ground. The time taken for the ball to strike the ground is
08:05View SolutionThe position of a particle along X-axis at time t is given by `x=2+t-3t^(2)`. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
08:27View SolutionA stone is allowed to fall freely from rest. The ratio of the time taken to fall through the first metre and the second metre distance is
03:03View SolutionWhich of the following represents uniformly accelerated motion ?
02:39View SolutionA particle moves along a straight line. Its position at any instant is given by `x = 32t-(8t^3)/3` where x is in metres and t in seconds. Find the acceleration of the particle at the instant when particle is at rest.
03:14View SolutionA point moves in a straight line so it's displacement `x` meter at time `t` second is given by `x^(2)=1+t^(2)`. It's acceleration in `ms^(-2)` at time `t` second is .
06:55View SolutionThe displacement `x` of a particle varies with time `t` as `x = ae^(-alpha t) + be^(beta t)`. Where `a,b, alpha` and `beta` positive constant.
The velocity of the particle will.03:23View SolutionThe ration of the distance traversed, in successive intervals of time by a body, falling from rest, are
02:48View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
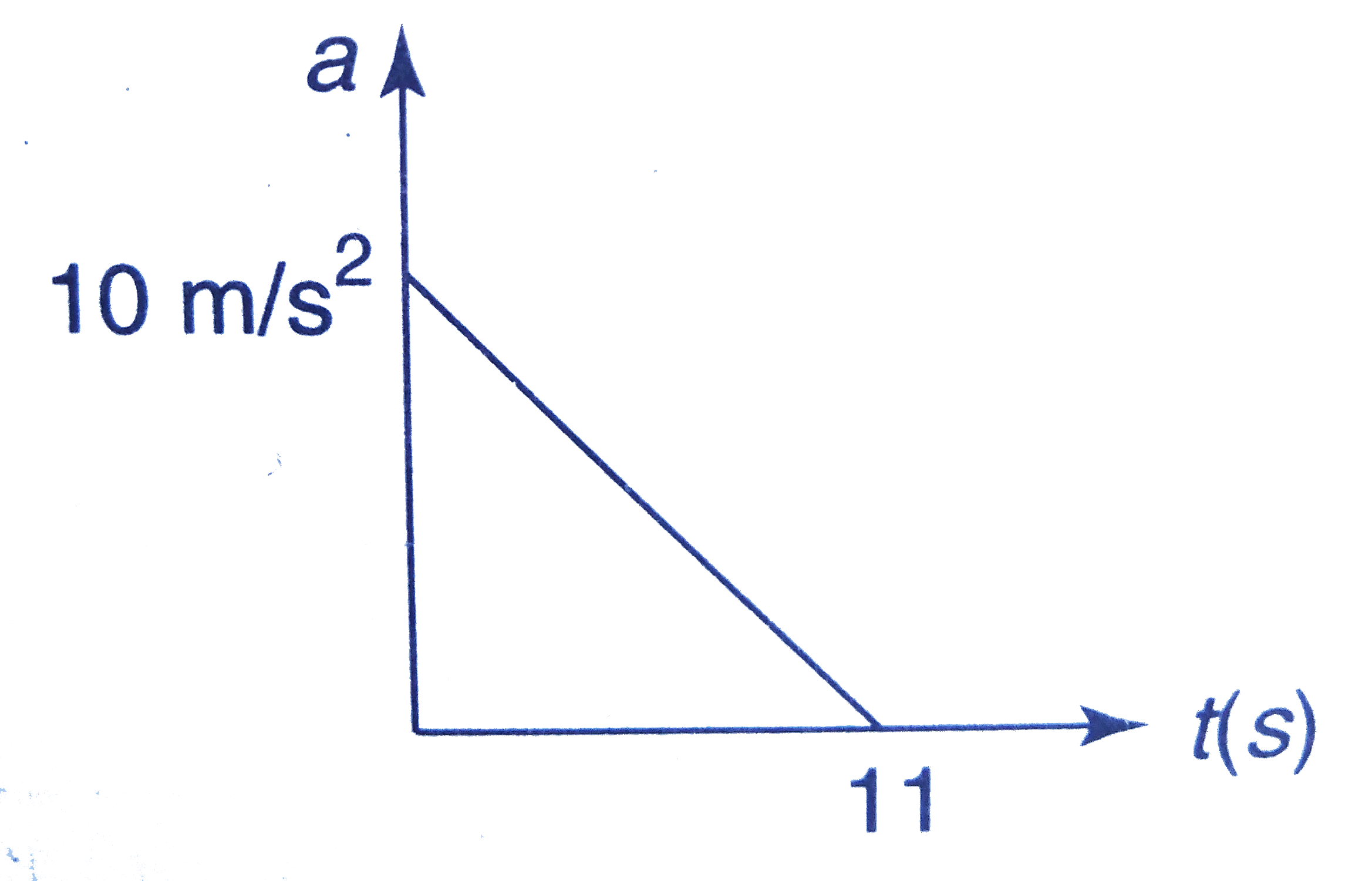 02:32View Solution
02:32View SolutionThe acceleration (a)-time(t) graph for a particle moving along a straight from rest is shown in figur. Which of the following graph is the best representation of its velocity (v) with time (t) ?
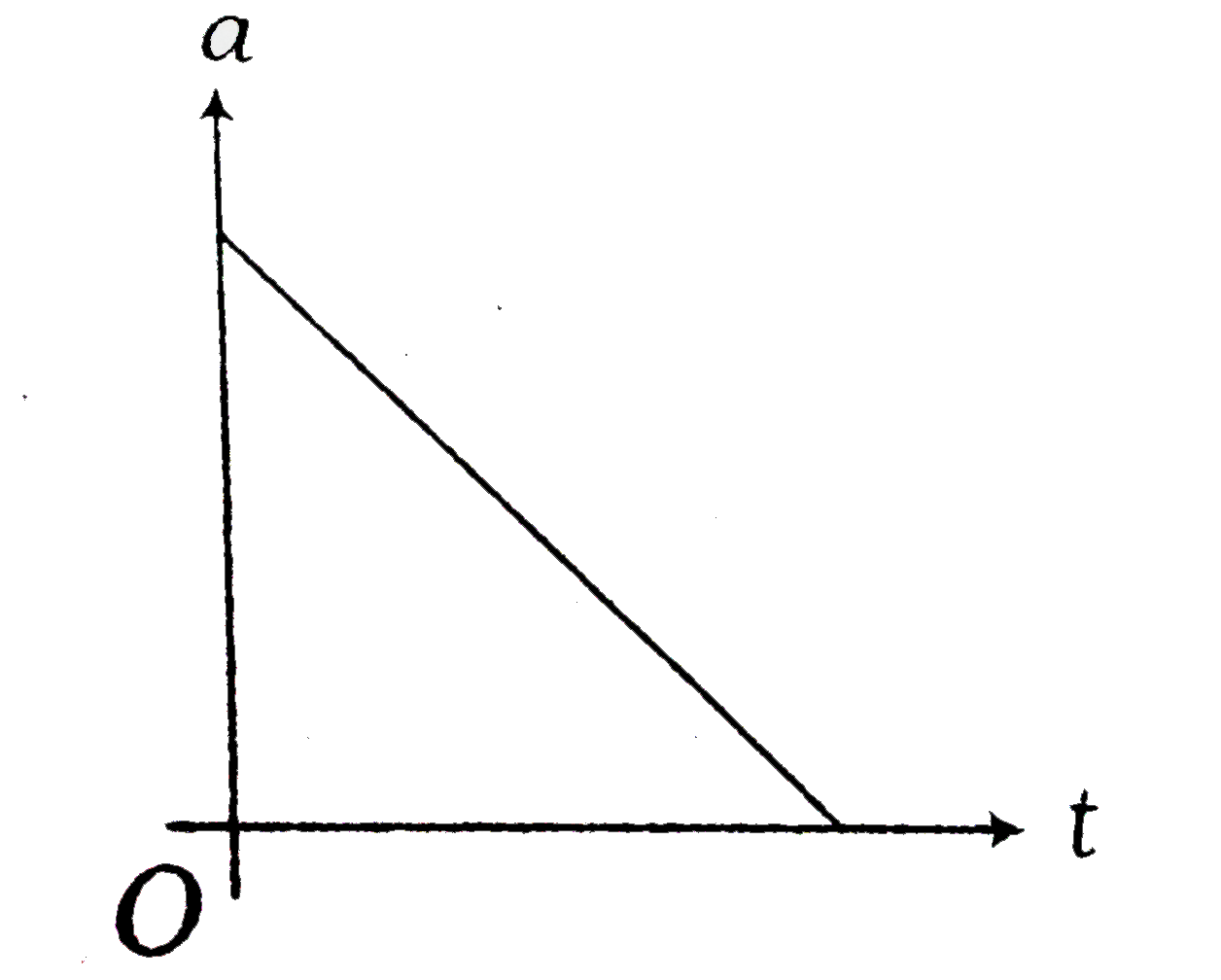 02:43View Solution
02:43View SolutionA point moves with uniform acceleration and `v_(1), v_(2)`, and `v_(3)` denote the average velocities in the three successive intervals of time `t_(1).t_(2)`, and `t_(3)` Which of the following Relations is correct?.
05:55View SolutionThe velocity-time graph for a particle moving along X-axis is shown in the figure. The corresponding displacement-time graph is correctly shown by
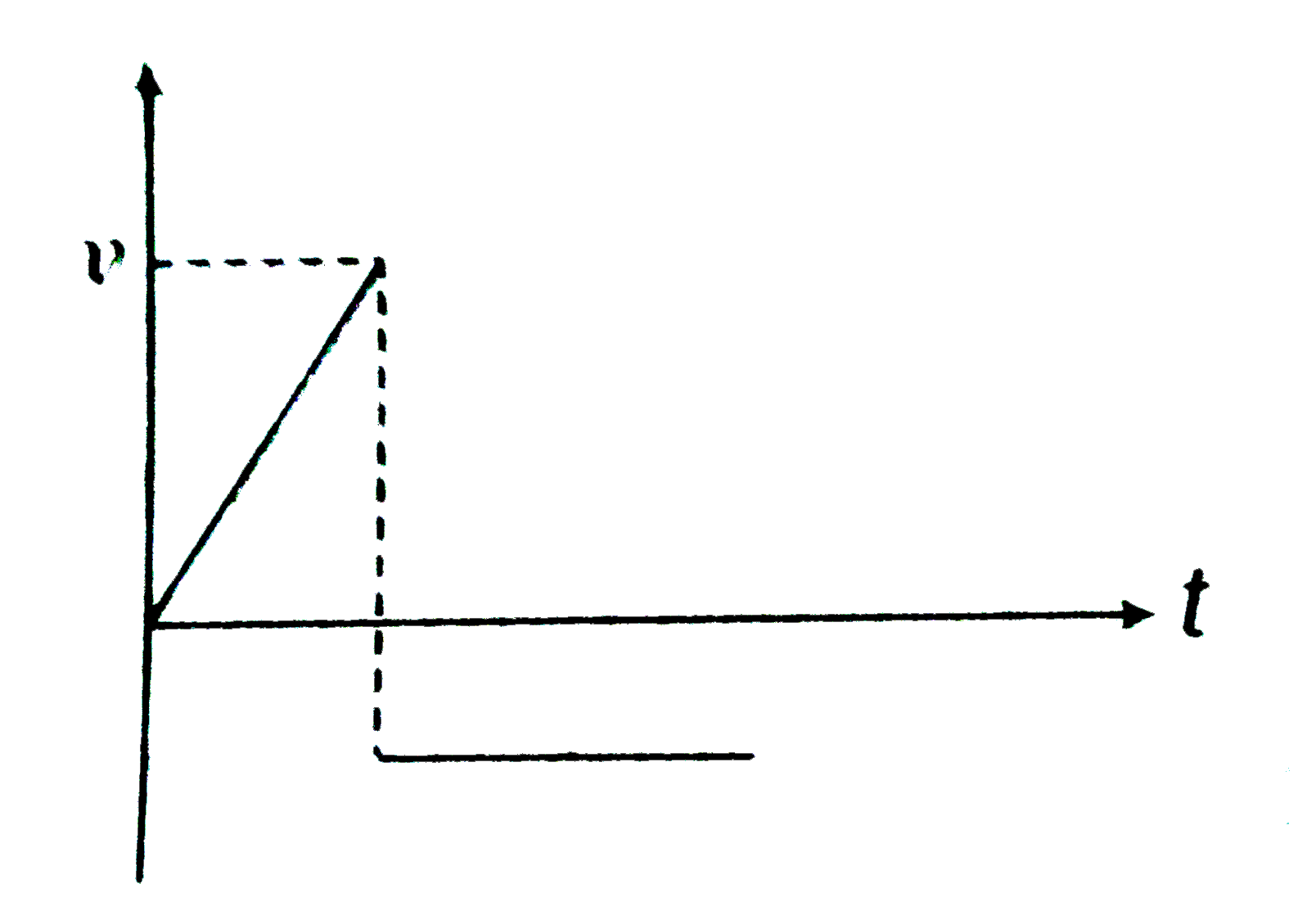 02:37View Solution
02:37View SolutionThe given graph shows the variation of velocity with displacement. Which one of the graphs given below correctly represents the variation of acceleration with displacement ?
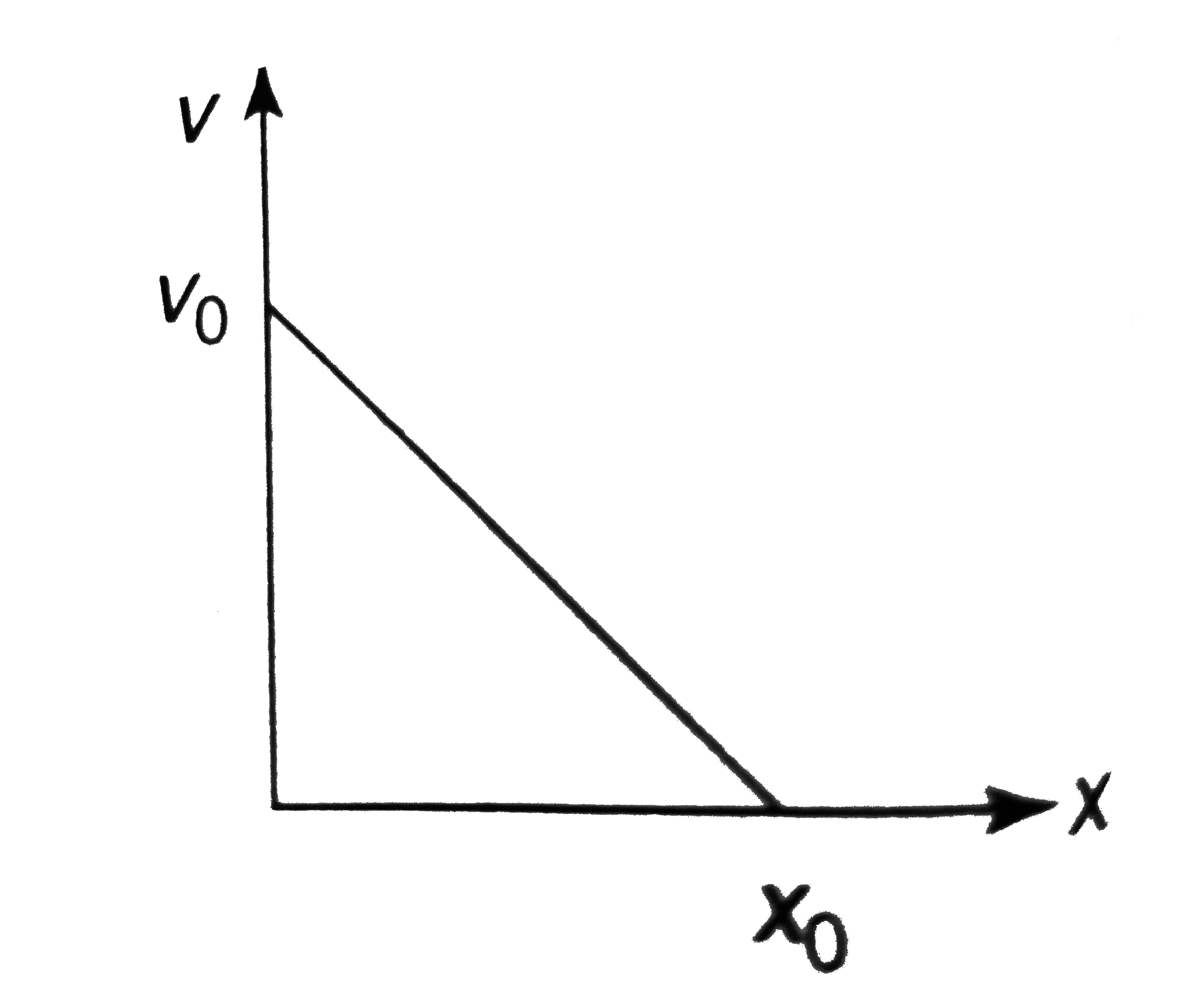 02:49View Solution
02:49View SolutionThe displacement x of a particle in a straight line motion is given by `x=1-t-t^(2)`. The correct representation of the motion is
03:02View SolutionThe verical of point above the ground is twice that of Q. A particle is projected downward with a speed of `5 ms^(-1)` from P and at the same time another particle is projected upward with the same speed from W. Both particle reach the ground simultaneously, then
04:17View SolutionAmong the four graphs shown in the figure there is only one graph for which average velocity over the time interval (0,T) can vanish for a suitably chosen `T`. Which one is it ?
01:50View SolutionA lift is coming from `8th` floor and is just about to reach `4th` floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct ?
01:58View SolutionIn one dimensional motion, instantaneous speed `v` satisfies `(0 le v lt v_0)`.
02:07View SolutionThe displacement of a particle is moving by `x = (t - 2)^2` where `x` is in metres and `t` in second. The distance covered by the particle in first `4` seconds is.
03:45View SolutionA partachutist after bailing out falls 50 m without friction. When parachute opens, it decelerates at `2 ms^(-2)`. At what height did he bail out
03:34View SolutionThe velocity `(upsilon)` of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
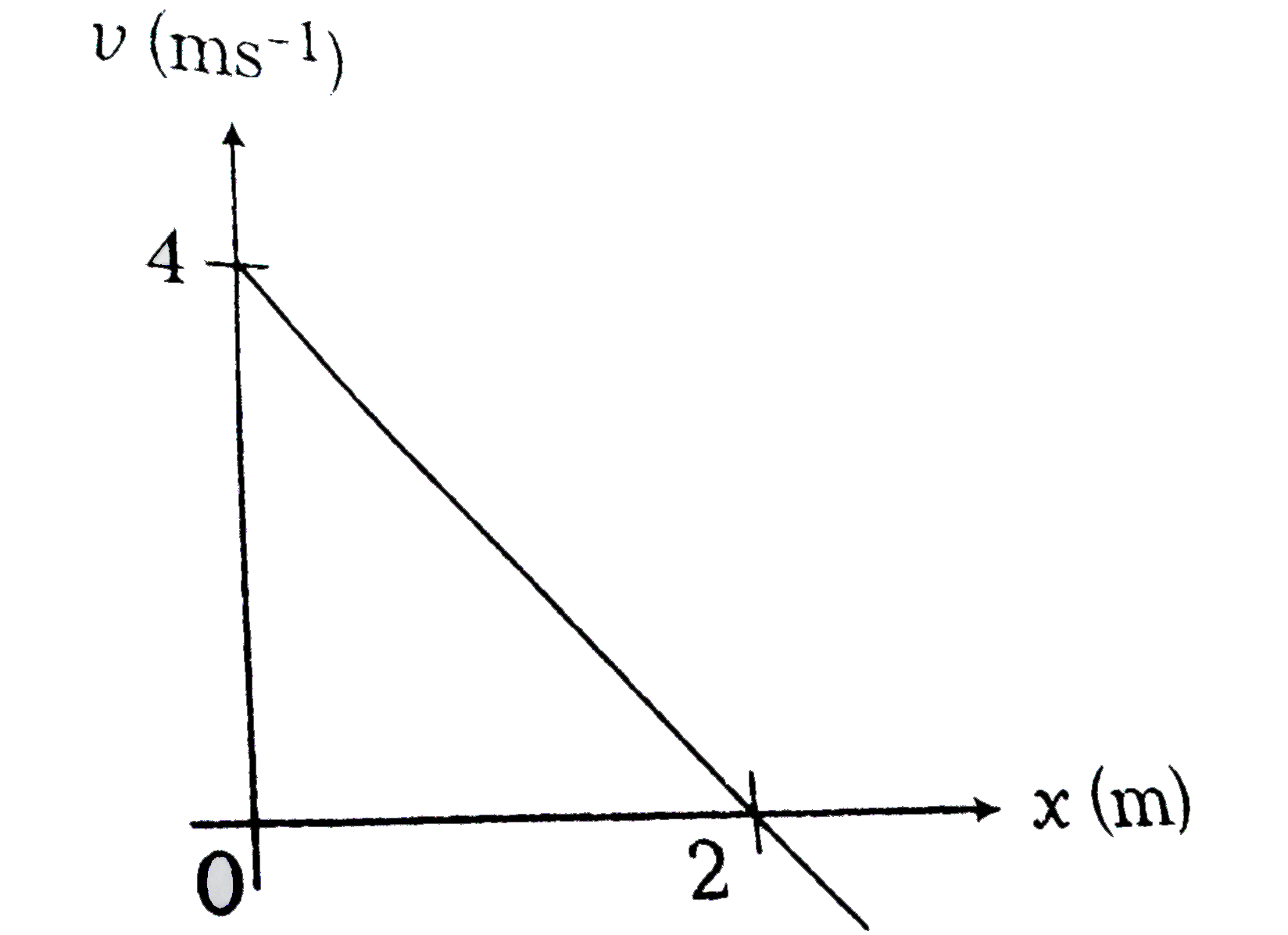 02:26View Solution
02:26View SolutionA car A moves along north with velocity 30 km/h and another car B moves along east with velocity 40 km/h. The relative velocity of A with respect to B is
03:29View SolutionRain is falling vertically downward with velocity `4m//s.` A man is moving horizontally with velocity `3 m//s`, the velocity of rain with respect to man is
03:44View SolutionA ship is travelling due east at a speed of `15 km//h.` Find the speed of a boat heading `30^@` east of north if it appears always due north from the ship.
04:22View SolutionA man takes `3 h` to cover a certain distance along the flow and takes `6h` to cover the same distance opposite to flow. In how much time, he will cross this distance in still water.
02:49View SolutionA river `500m` wide is flowing at a rate of `4 m//s.` A boat is sailing at a velocity of `10 m//s` with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
03:17View SolutionA ball is dropped vertically from `a` height `d` above the ground . It hits the ground and bounces up vertically to a height ` (d)//(2). Neglecting subsequent motion and air resistance , its velocity `v` varies with the height `h` above the ground as
04:50View SolutionThe driver of a train moving at a speed ` v_(1)` sights another train at a disane ` d`, ahead of him moving in the same direction with a slower speed ` v_(2)`. He applies the brakes and gives a constant teradation ` a` to his train. Show that here will be no collision if ` d gt (v_(1) -v_(2))^(2) //2 a`.
04:15View SolutionA boat which has a speed of `5 km` per hour in still water crosses a river of width 1 km along the shortest possible path in fifteen minutes. The velocity of the river water in km per hour is :-
02:11View SolutionTwo car `A` and `B` travelling in the same direction with velocities `v_1` and `v_2(v_1 gt v_2)`. When the car `A` is at a distance `d` ahead of the car `B`, the driver of the car `A` applied the brake producing a uniform retardation `a`. There wil be no collision when.
04:28View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. `(g = 10 ms^-2)`
06:13View SolutionA ball is thrown vertically up with a velocity `u`. It passes three points `A, B` and `C` in its upward journey with velocities `u/2, u/3` and `u/4`, respectively. Find `(AB)/(BC)`.
04:28View SolutionA particle moving along x-axis has acceleration `f`, at time `t`, given by `f = f_0 (1 - (t)/(T))`, where `f_0` and `T` are constant.
The particle at `t = 0` has zero velocity. In the time interval between `t = 0` and the instant when `f = 0`, the particle's velocity `(v_x)` is :03:18View SolutionThe position `x` of a particle with respect to time `t` along the x-axis is given by `x=9t^(2)-t^(3)` where `x` is in meter and `t` in second. What will be the position of this particle when it achieves maximum speed along the positive `x` direction
02:11View SolutionTwo particles P and Q simultaneously start moving from point A with velocities `15 m//s` and `20 m//s` respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When P overtakes Q at point B then its velocity is `30 m//s`, the velocity of Q at point B will be
04:01View SolutionA body falling from a high mimaret travels 40 meters in the last 2 seconds of its fall to ground. Height of minaret in meters is (take `g=10(m)/(s^2)`)
02:30View SolutionA small block slides without friction down an iclined plane starting form rest. Let `S_(n)` be the distance traveled from time `t = n - 1` to `t = n`. Then `(S_(n))/(S_(n + 1))` is:
05:25View SolutionA particle located at `x = 0` at time `t = 0`, starts moving along with the positive ` x-direction` with a velocity 'v' that varies as ` v = a sqrt(x)`. The displacement of the particle varies with time as
03:56View SolutionA body falls freely from the top of a tower. It covers 36% of the total height in the lkast second before striking the ground level. The height of the tower is
04:22View SolutionAn elevator car whose floor to ceiling distance is equal to `2.7 m` starts ascending with constant acceleration `1.2 m//s^(2)`, 2 sec after the start a bolt begins falling from the ceiling of the car. Answer the following question `(g=9.8 m//s^(2))`
The bolt's free fall time is16:48View Solution
(A) Taking it together questions and complete solutions for chapter MOTION IN A PLANE of DC PANDEY PHYSICS (HINGLISH) of Class 11
