Complete Solutions to Level 2 Single Correct of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Level 2 Single Correct |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
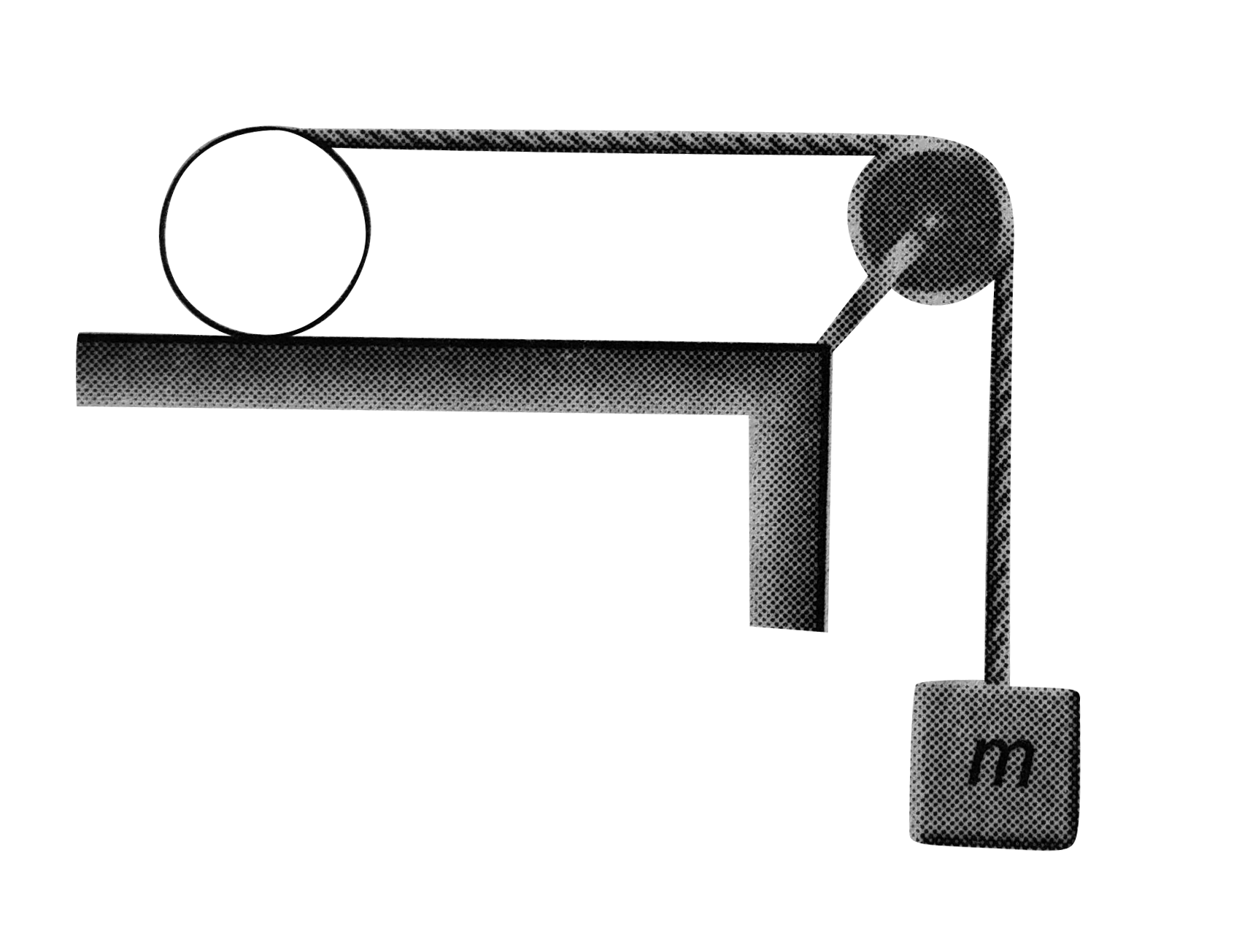
in the given figure a ring of mass `m` is kept on a horizontal surface while a body of equal mass `m` si attached through string, which is wounded on the ring. When the system is released the ring rolls without slipping. consider the following statement and choose the correct options.
(i). Acceleration of centre of mass of ring is `(2g)/(3)`
(ii). acceleration of hanging particle is `(4g)/(3)`
(iii). Frictional force (on the ring) acts in backward direction.
(iii). Frictional force (on the ring) acts in backward direction
(iv) . Fraction force (on the ring) acts in backward direction.
View Solution
A solid sphere of mass 10 kg is placed on a rough surface having coefficient of friction `mu=0.1A` constant force `F=7N` is applied along a line passing through the centre of the sphere as shown in the figure. The value of frictional force on the sphere is
View Solution
From a uniform square plate of side a and mass `m`, a square portion DEFG of side `(a)/(2)` is removed. Then, the moment of inertia of remaining portion about the axis AB is
View Solution
A small solid sphere of mass `m` and radius `r` starting from rest from the rim of a fixed hemispherical bowl of radius `R(gt gtr)` rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere is
View Solution
A uniform solid cylinder of mass `m` and radius `R` is placed on a rough horizontal surface. A horizontal constant force `F` is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionIn the above question, the frictional force on the cylinder is
View Solution
A small pulley of radius 20 cm and moment of inertia `0.32kg-m^(2)` is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition acceleration of the block will be
View Solution
A uniform circular disc of radius `R` is placed on a smooth horizontal surface with its plane horizontal and hinged at circumference through point O as shown . An impulse P is applied at a perpendicular distance `h` from its centre C. The value of h so that the impulse due to hinge is zero, is
View Solution
A rod is supported horizontally by means of two strings of equal length as shown in figure. If one of the string is cut. Then tension in other string at the same instant will.
View Solution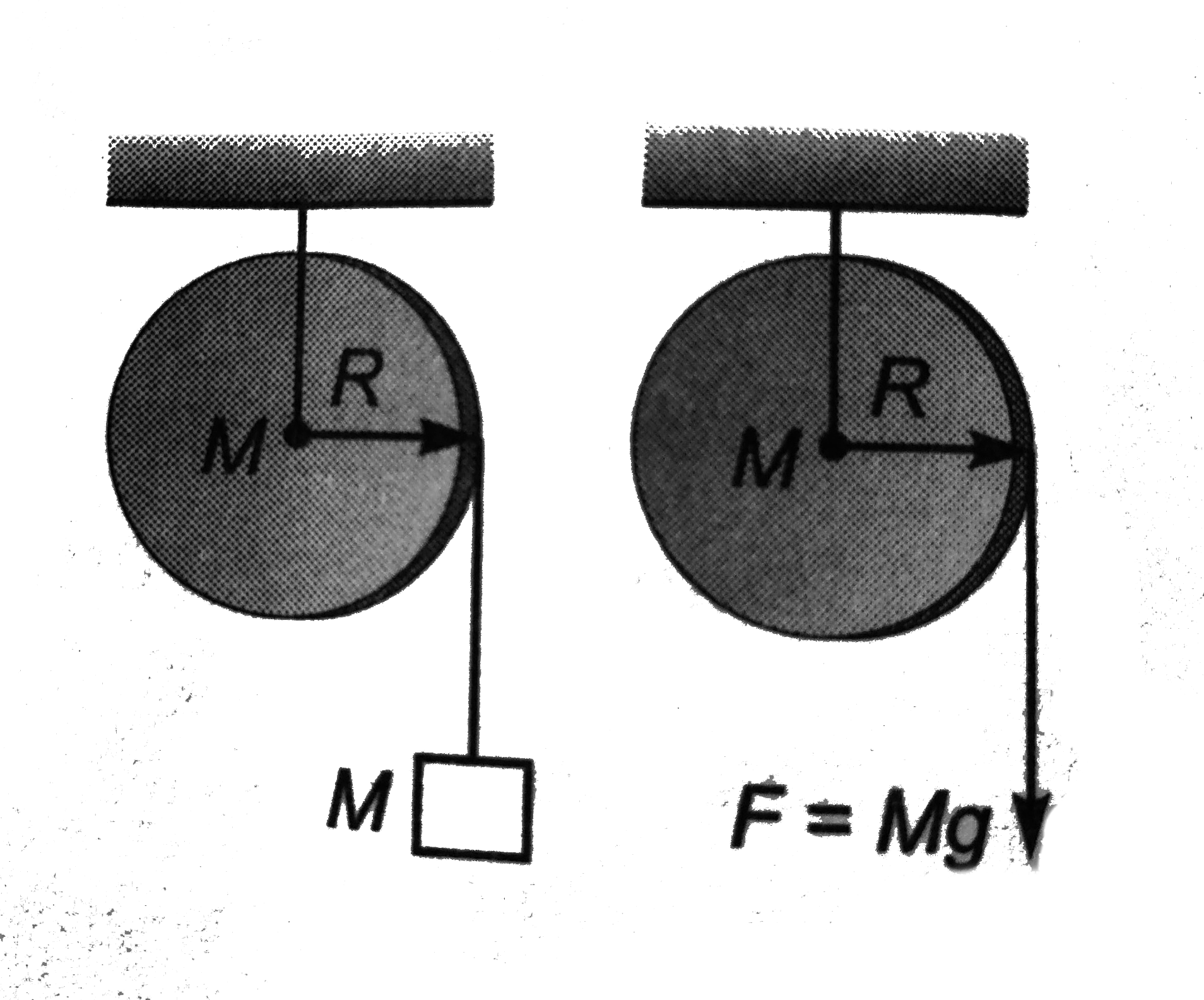
The figure represent two cases. In first case a block of mass `M` is attached to a string which is tightly wound on a disc of mass `M` and radius `R`. In second case `F=Mg` initially the disc is stationary in each case. if the same length of string is unwound from the disc, then
View Solution
A uniform cylinder of mass `M` and radius `R` is released from rest on a rough inclined surface of inclination `theta` with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness `k` is
View SolutionA uniform rod of mass `m` and length `l` rotates in a horizontal plane with an angular velocity `omega` about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution
A rod of length 1 m rotates in the xy plane about the fixed point O in the anticlockwise sense, as shown in figure with velocity `omega=a+bt` where `a=10rads^(-1)` and `b=5rads^(-2)`. The velocity and acceleration of the point A at `t=0` is
View Solution
A ring of radius `R` rolls on a horizontal surface with constant acceleration `a` of the centre of mass as shown in figure. If `omega` is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound is
View SolutionThe density of a rod AB increases linearly from A to B its midpoint is O and its centre of mass is at C. four axes pass through A, B, O and C, all perpendicular to the length of the rod. The moment of inertial of the rod about these axes are `I_(A), I_(B), I_(O)` and `I_(C)` respectively.
View Solution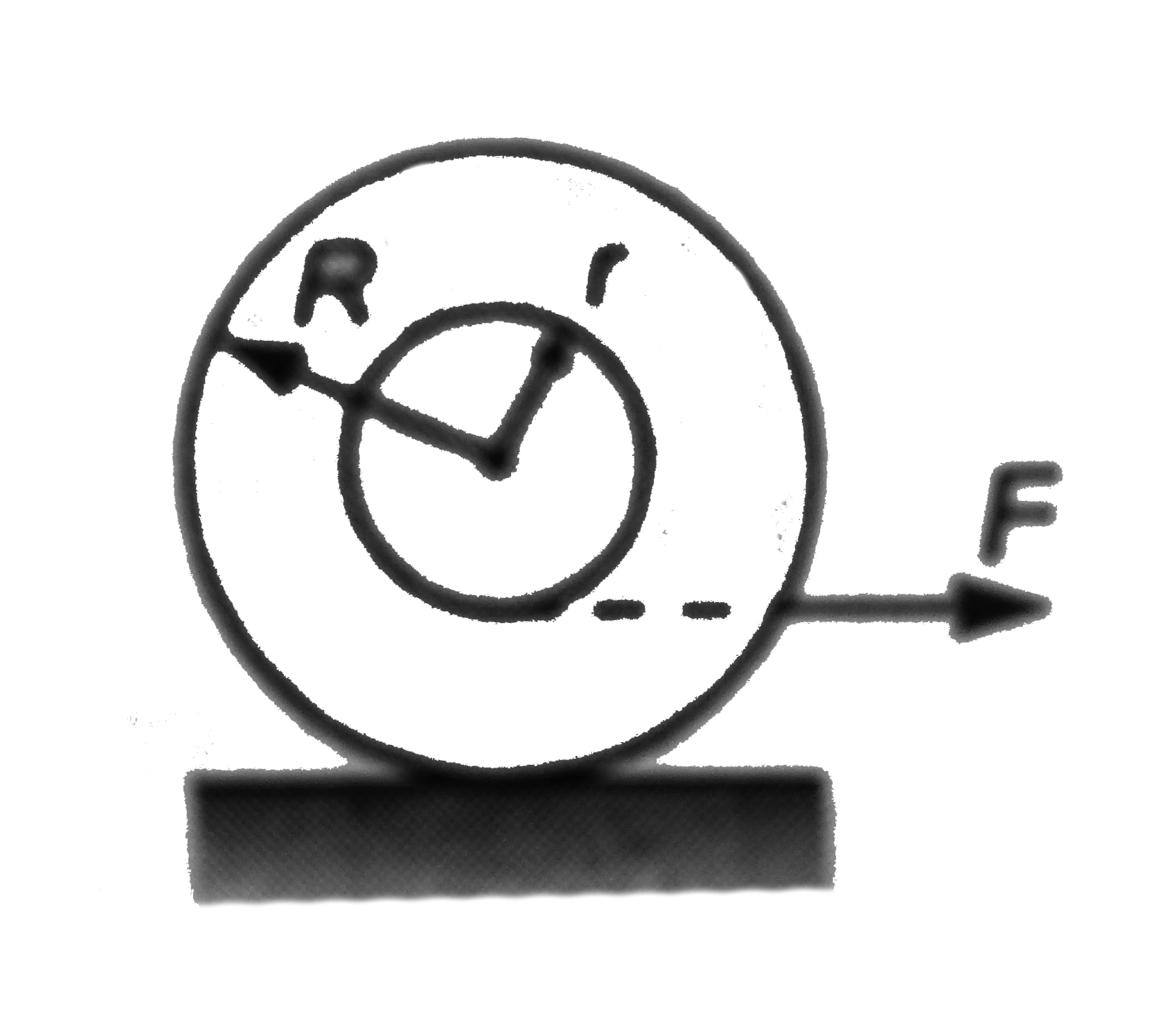
The figure shows a spool placed at rest on a horizontal rough surface. A tightly wound string on the inner cylinder is pulled horizontally with a force F. identify the correct alternative related to the friction f acting on the spool
View Solution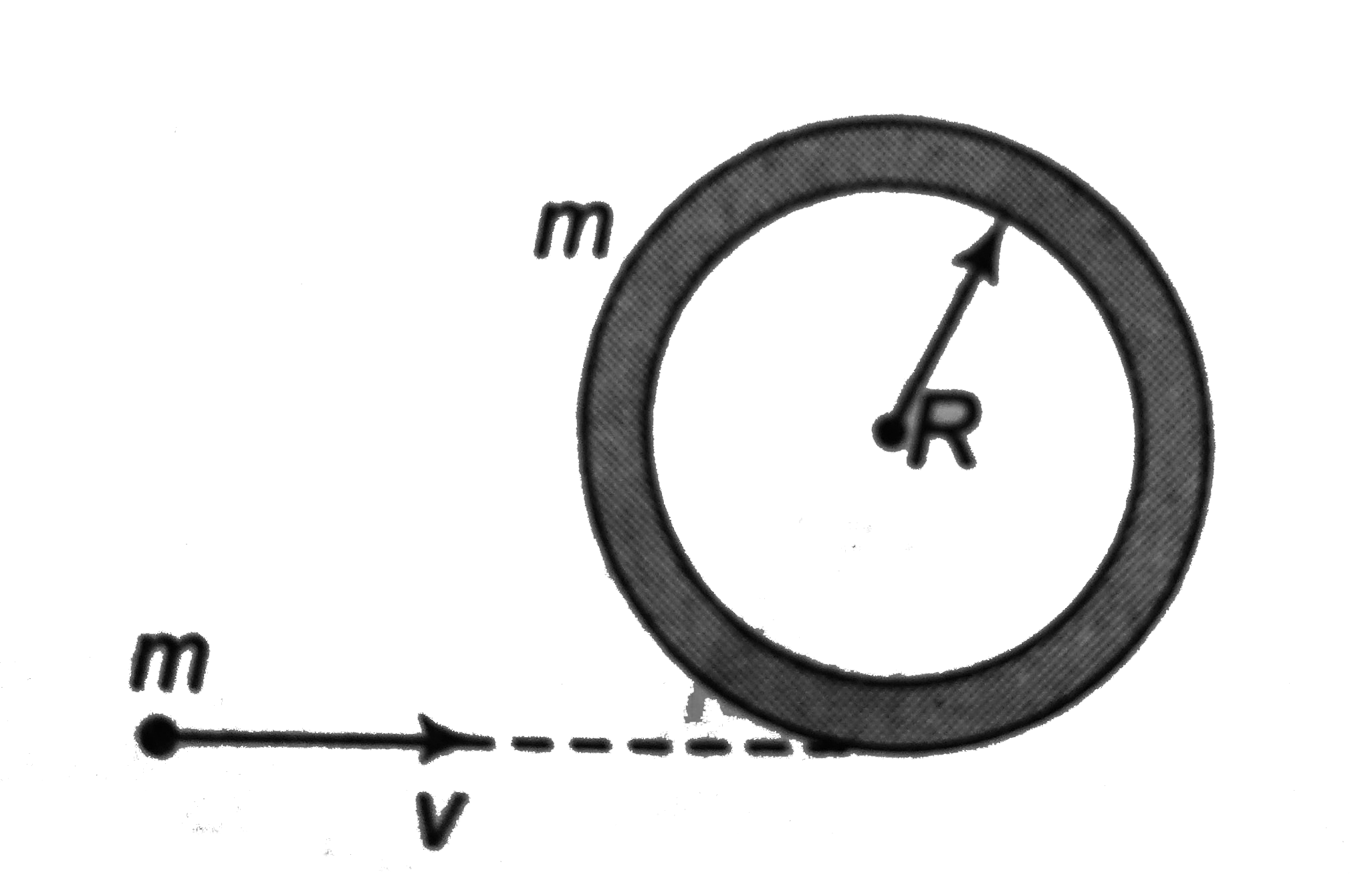
A circular ring of mass `m` and radius `R` rests flat on a horizontal smooth surface as shown in figure. A particle of mass `m`, and moving with a velocity `v`. Collides inelastically `(e=0)` with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View Solution
A stationary uniform rod in the upright position is allowed to fall on a smooth horizotal surface. The figure shows the instantaneous position of the rod. Identify the correct statement.
View SolutionA thin unifrom rod of mass `m` and length `l` is free to rotate about its upper end When it is at rest. It receives an impulse `J` as its lowest point, normal to its length immediately after impact.
View Solution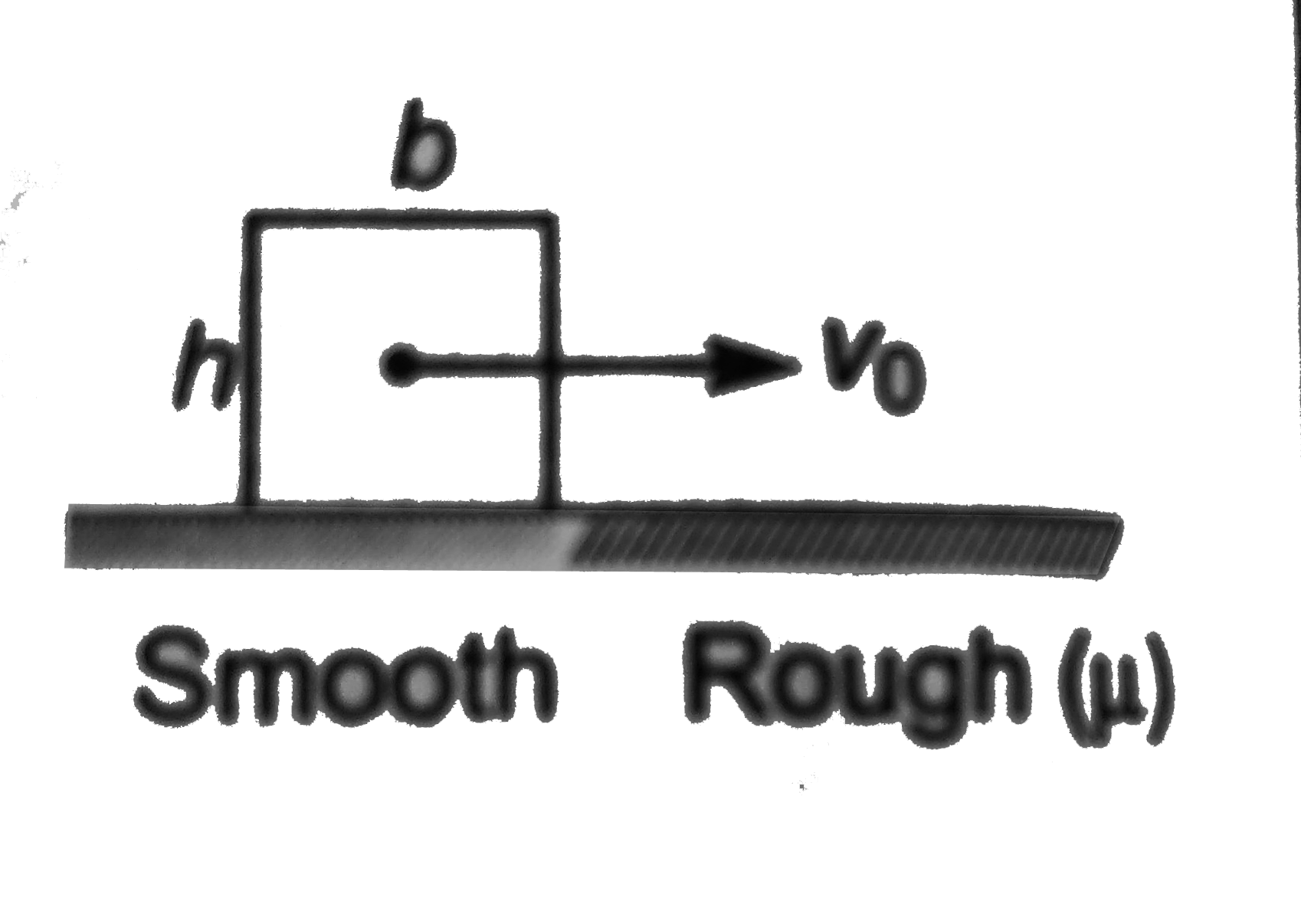
A rectangular block of size `(bbxxh)` moving with velocity `v_(0)` enters on a rough surface where the coefficient of friction is `mu` as shown in figure. Identify the correct statement.
View Solution
A uniform rod of length `L` and mass `m` is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass `m` is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View Solution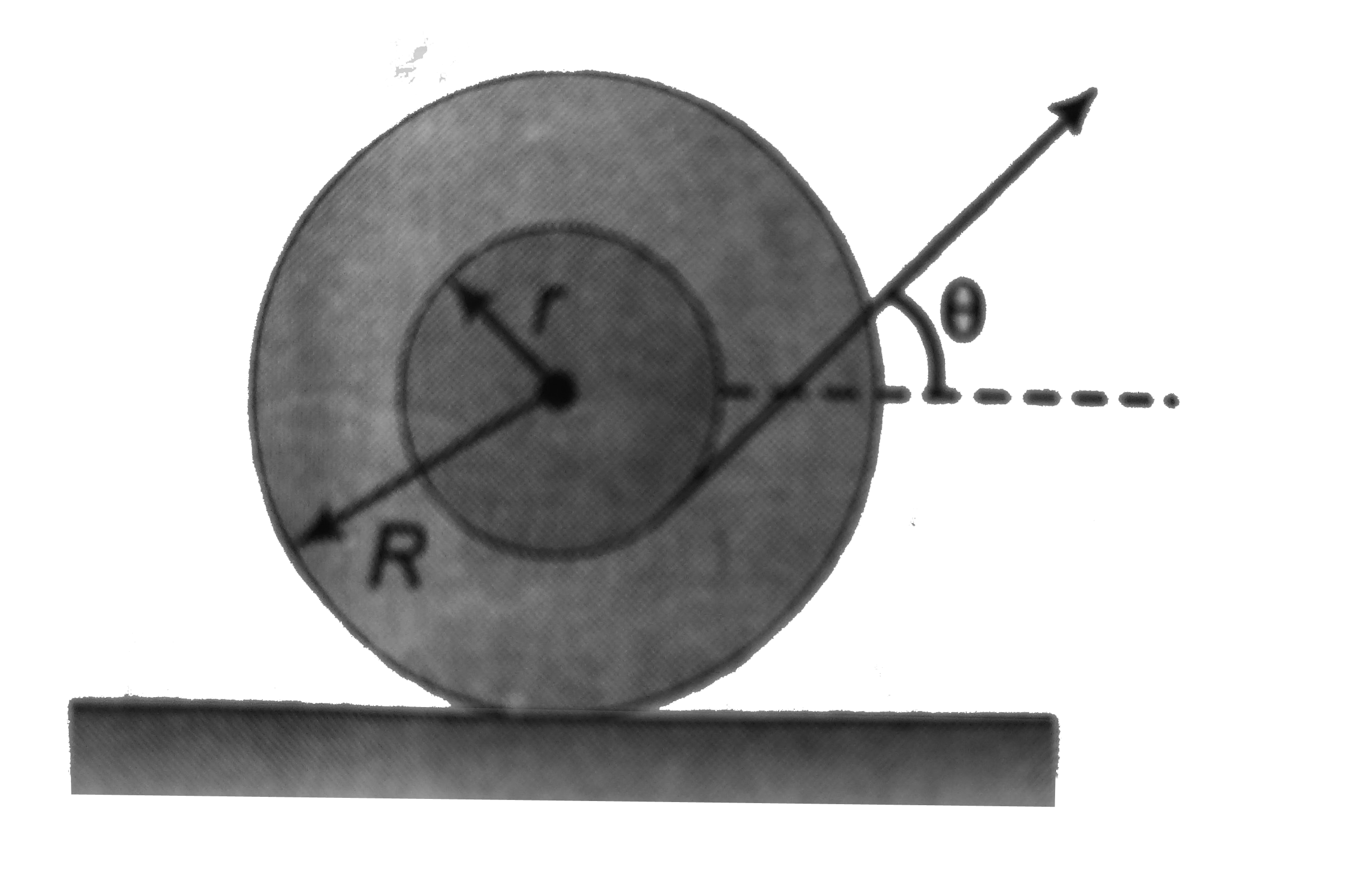
A spool is pulled at an angle `theta` with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle `theta` is equal to
View Solution
Uniform rod AB is hinged at end A in horizontal position as shown in the figure. The other end is connected to a block through a massless string as shown. The pulley is smooth and massless. Mass of block and rod is same and is equal to `m` Then acceleration of block just after release from this position is
View Solution
A cylinder having radius 0.4 m initially rotating (at `r=0`) with `omega_(0)=54rad//s` is placed on a rough inclined plane with `theta=37^(@)` having friction coefficient `mu=0.5` the time taken by the cylinder to start pure rolling is `(g=10m//s^(2))`
View Solution
A disc of mass `M` and radius `R` is rolling purely with centre's velcity `v_(0)` on a flat horizontal floor when it hits a step in the floor of height `R//4` The corner of the step is sufficiently rough to prevent any slippoing of the disc against itself. What is the velocity of the centre of the disc just after impact?
View Solution
A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction `=mu`) with speed of centre `=u`. It collides in-elastically with a smooth vertical wall at a certain moment, the coefficient of restituting being `(1)/(2)`. The sphere will begin pure rolling after a time.
View Solution
Level 2 Single Correct questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions