Complete Solutions to Assertion And Reason of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Assertion And Reason |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
Assertion: Moment of inertia of a rigid body about any axis passing through its centre of mass is minimum
Reason: From theorem of parallel axis
`I=I_(cm)+Mr^(2)`
View SolutionAssertion: A ball is released on a rough ground in the condition shown in figure. it will start pure rolling after some time towards left side.
Reason: Friction will convert the pure rotational motion of the ball into pure rolling
View SolutionAssertion: A solid sphere and a hollow sphere are rolling on ground with same total kinetic energies. if translational kinetic energy of solid sphere is K, then translational kinetic energy of follow sphere should be greater than K.
Reason: In case of hollow sphere rotational kinetic energy is less than its translational kinetic energy.
View Solution
A small ball is released from rest from point A as shown. if bowl is smotth, than ball will exert more pressure at point B, compared to the situation if bowl is rough.
Reason: Linear velocity and hence, centripetal force in smooth situation is more.
View SolutionAssertion: A cubical block is moving on a rough ground with velocity `v_()`. During motion net normal reaction on the block from ground will not pass through centre of cube. it will shift towards right.
Reason: It is to keep the block is rotational equilibrium
View SolutionAssertion: A ring is rolling without slipping on a rough ground. It strikes elastically with a smooth wall as shown in figure. Ring will stop after some time while travelling in opposite direction.
Reason: After impact net angular momentum about an axis passing through bottommost point and perpendicular to plane of paper is zero.
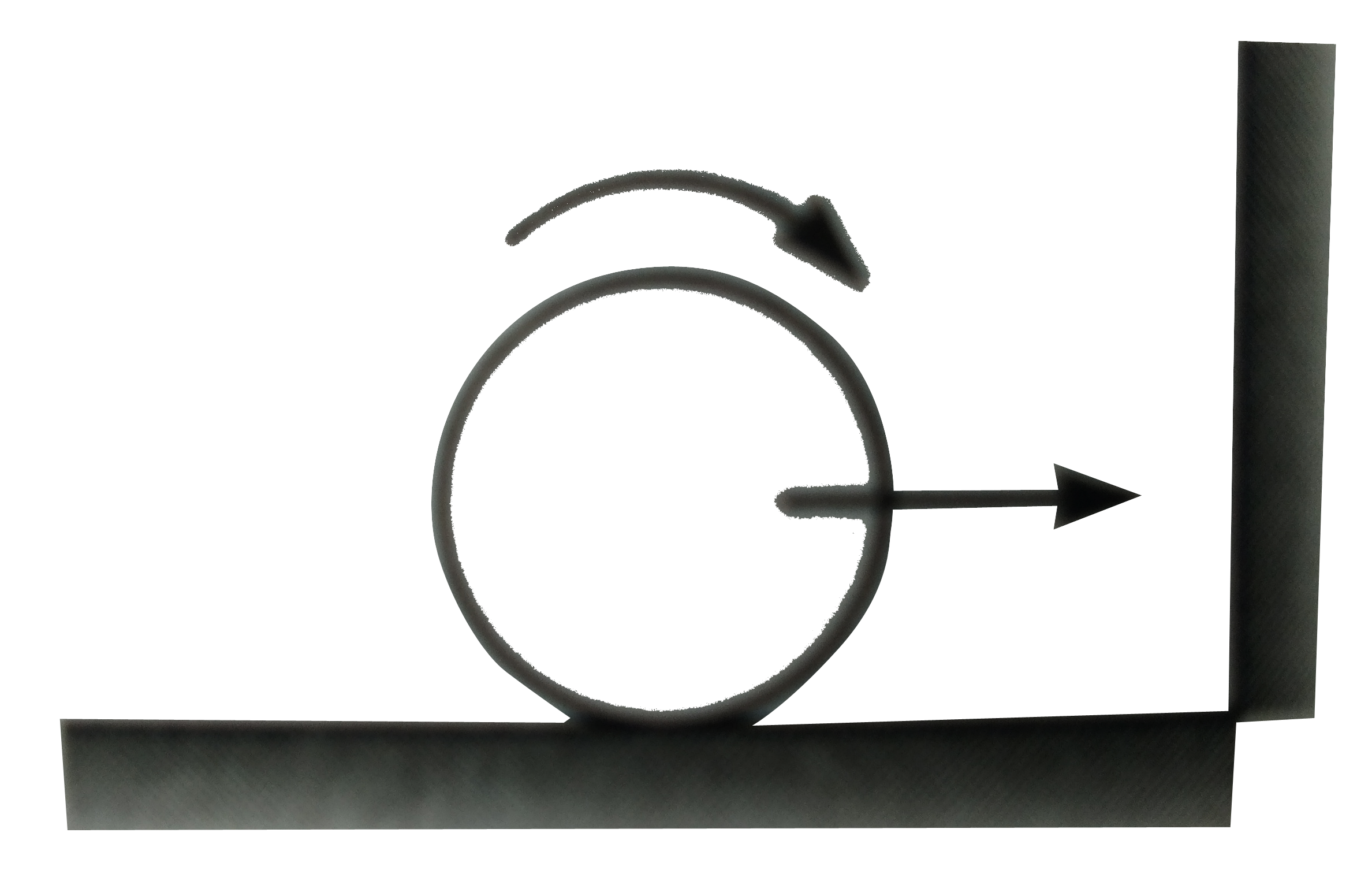
View Solution
Assertion: There is a thin rod AB and a dotted line CD. All the axes we are talking about are perpendicular to plane . As we take different axes moving from A to D, moment of inertia of the rod may first decrease then increase.
Reason: Theorem of perpendicular axis cannot be applied here.
View SolutionAssertion: If linear momentum of a particle is constant, then its angular momentum about any point will also remain constant.
Reason: Linear momentum remains constant if `F_(n et)=0` and angular momentum remains constant if `tau_(n et)=0`
View Solution
In the figure shown A, B and C are three points on the circumference of a disc. Let `v_(A),v_(B)` and `v_(c)` are speeds of these three points then
`v_(c)gtv_(B)gtv_(A)`
Reason: In case of rotaional plus translational motion of a rigid body, net speed of any point (other than centre of mass) is greater than, less than or equal to the speed of centre of mass.
View Solution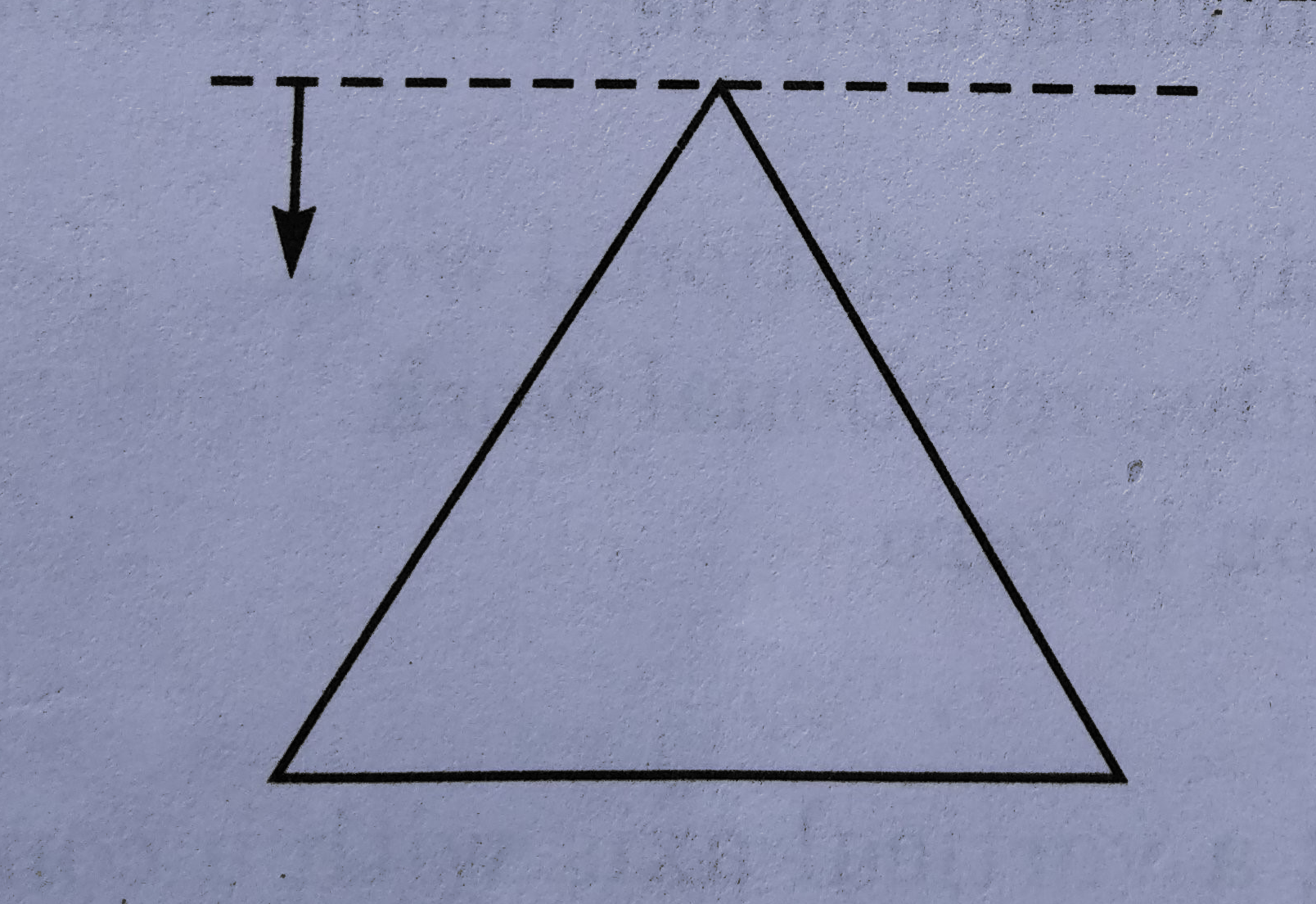
There is a triangular plate as shown. A dotted axis is lying in the plane of slab. As the axis is moved downwards, moment of inertia of slab will first decrease then increase.
Reason: Axis is first moving towards its centre of mass and then it is receding from it.
View Solution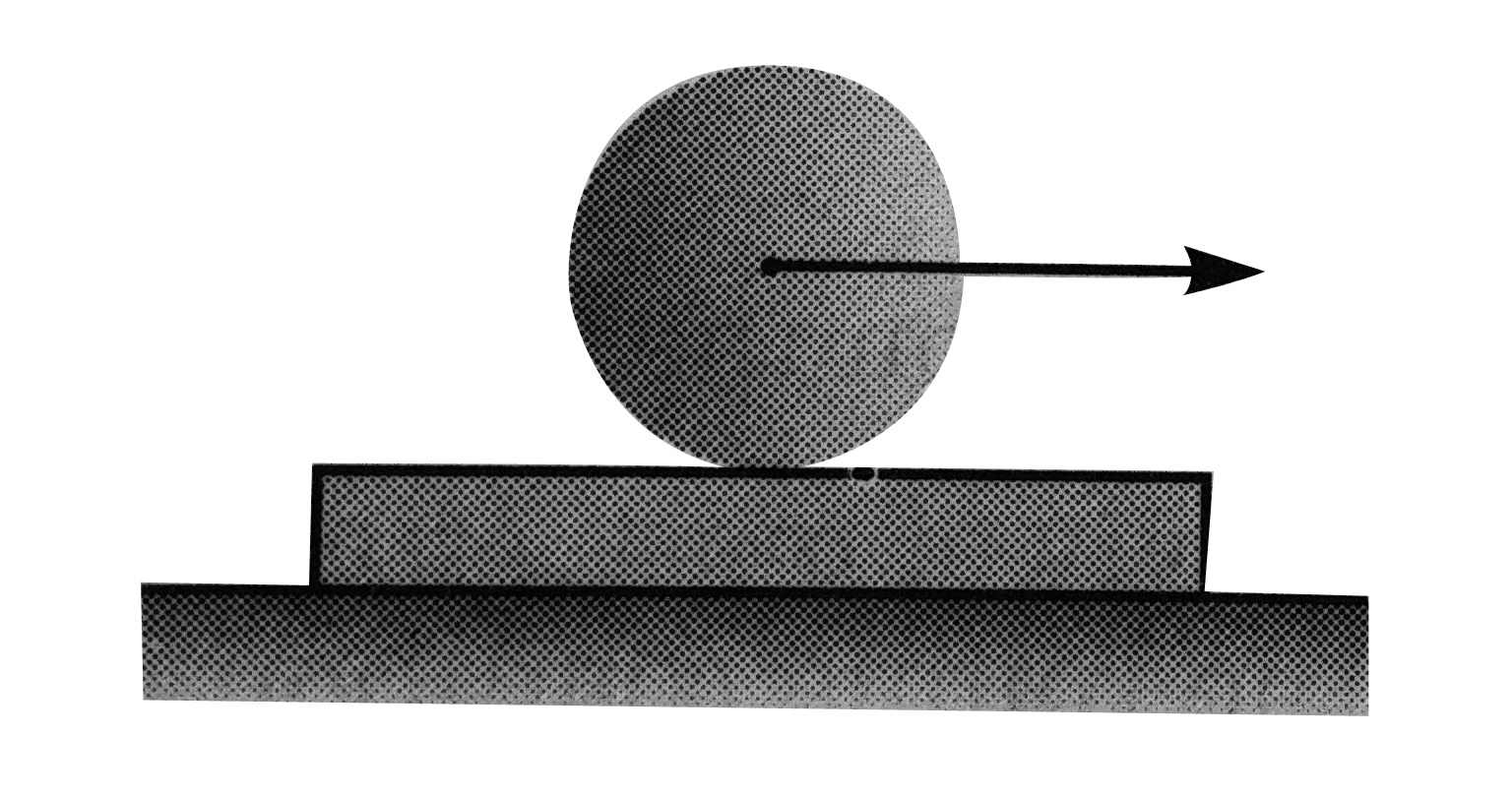
A horizontal force `F` is applied at the centre of solid sphere placed over a plank. The minimum coefficient of friction between plank and sphere required for pure rolling is `mu_(1)` when plank is kept at rest ad `mu_(2)` when plank can move, then `mu_(2)ltmu_(1)`
Reason: Work done by frictional force on the sphere in both cases is zero.
View Solution
Assertion And Reason questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions