Complete Solutions to Level 1 Subjective of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
If radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc equals ilts radius. Find the distance of the line from the centre.
View SolutionFind the moment of inertia of a uniform square plate of mass `M` and edge a about one of its diagonals.
View SolutionMoment of inertia of a uniform rod of mass `m` and length `l` is `(7)/(12)ml^(2)` about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
View SolutionTwo point masses `m_(1)` and `m_(2)` are joined by a weightless rod of length `r`. Calculate the moment of inerrtia of the system about an axis passing through its centre of mass and perpendicular to the rod.
View SolutionRadius of gyration of a body about an axis at a distance 6 cm from its centre of mass is 10 cm. Find its radius of gyration about a parallel axis through its centre of mass.
View SolutionA wheel rotates around a stationary axis so that the rotation angle `theta` varies with time as `theta=at^(2)` where `a=0.2rad//s^(2)`. Find the magnitude of net acceleration of the point A at the rim at the moment `t=2.5s` if the linear velocity of the point A at this moment is `v=0.65m//s`.
View Solution
Particle `P` shown in figure is moving in a circle of radius `R=10` cm with linear speed `v=2m//s` Find the angular speed of particle about point O.
View SolutionA particle of mass `m` is projected from the ground with an initial speed `u` at an angle `alpha`. Find the magnitude of its angular momentum at the highest point of its trajector about the point of projection.
View SolutionLinear mss density (mass/length) of a rod depends on the distanec from one end (say A) as `lamda_(x)=(alphax+beta)` here `alpha` and `beta` are constants, find the moment of inertia of this rod about an axis passing through `A` and perpendicular to the rod. Length of the rod is `l`.
View SolutionWhen a body rolls, on a stationary ground, the acceleration of the point of contact is always zero. Is this statement true or false?
View SolutionA solid sphere of mass `m` rolls down an inclined plane a height `h`. Find rotational kinetic energy of the sphere.
View SolutionThe topmost and bottommost velocities of a disc are `v_(1)` and `v_(2)(ltv_(1)` in the same direction. The radius is `R`. Find te value of angular velocity `omega`.
View SolutionA circular lamina of radius `a` and centre `O` has a mass per unit area of `kx^(2)`, where `x` is the distance from `O` and `k` is a constant. If the mass of the lamina is `M`, find in terms of `M` and `a`, the moment of inertia of the lamina about an axis through `O` and perpendicular to the lamina.
View SolutionA solid body starts rotating about a stationary axis with an angular acceleration `alpha=(2.0xx10^(-2))trad//s^(2)` here `t` is in seconds. How soon after the beginning of rotation will the total acceleration vector of an arbitrary point of the body form an angle `theta=60^(@)` with its velocity vector?
View Solution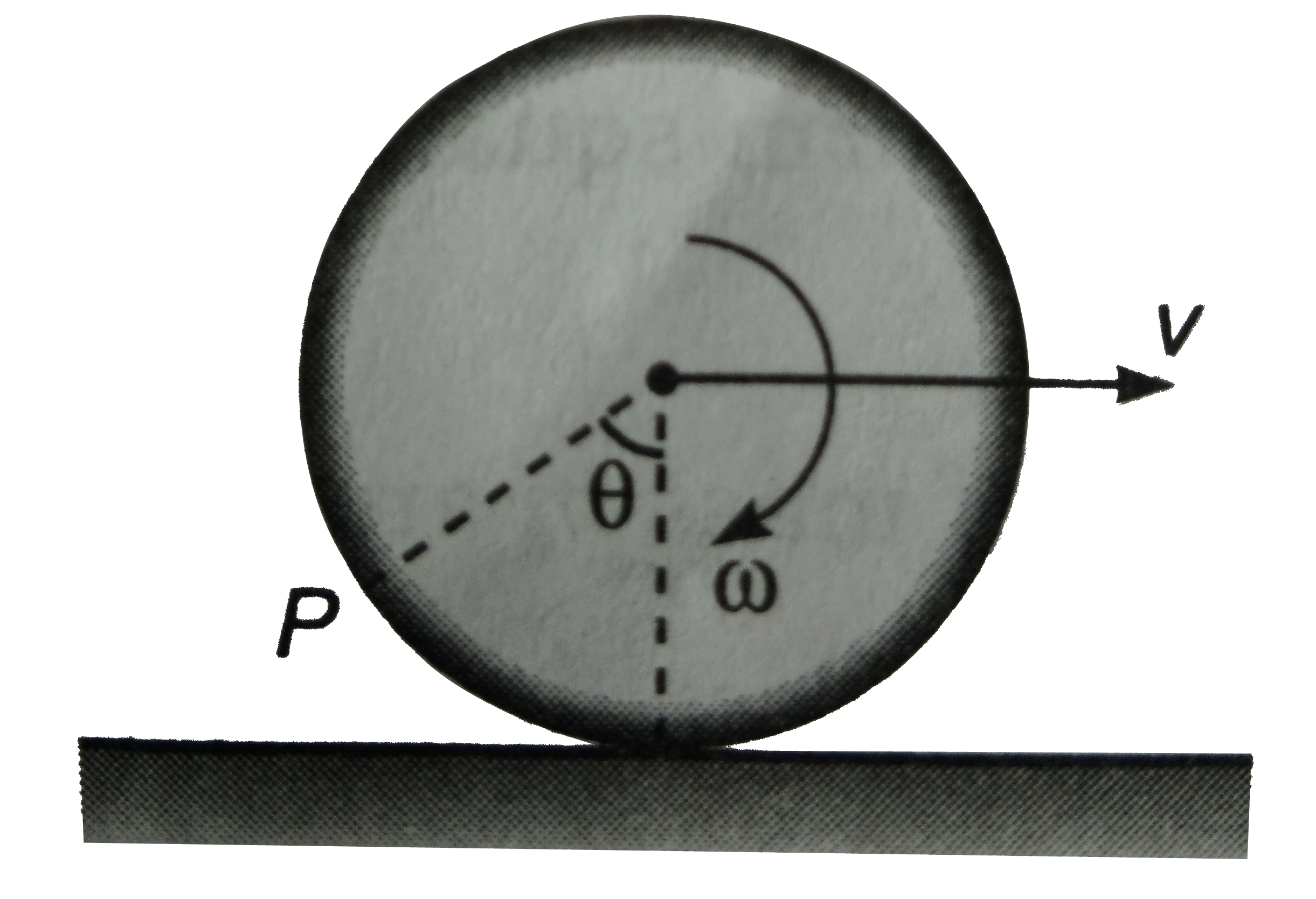
A ring of radius `R` rolls on a horizontal ground with linear speed `v` and angular speed `omega`. For what value of `theta` the velocity of point `P` is in vertical direction `(vltRomega)`.
View Solution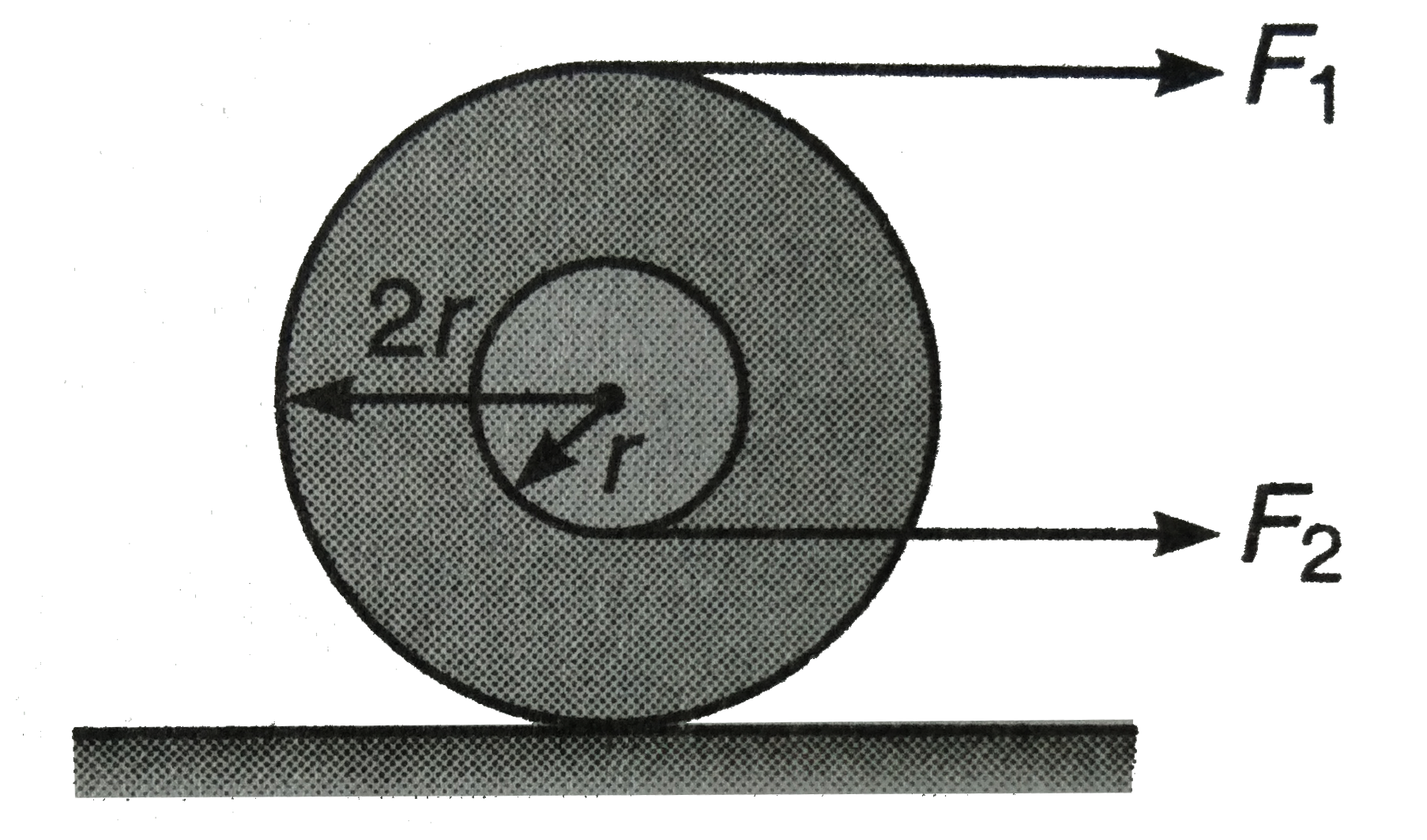
Two forces `F_(1)` and `F_(2)` are applied on a spool of mass `M` and moment of inertia `I` about an axis passing through its centre of mass. Find the ratio `(F_(1))/(F_(2))`. So that the force of friction is zero. Given that `Ilt2Mr^(2)`.
View SolutionA disc is placed on the ground. Friction coefficient is `mu`. What is the minimum force required to move the disc if it is applied at the topmost point?
View SolutionA cube is resting on an inclinded plane. If the angle of inclination is gradually increased. What must be the coefficient of friction between the cube and plane so that,
(a). Cube slides before toppling?
(b). Cube topplies before sliding?
View SolutionA uniform disc of mass 20 kg and radius 0.5 m can turn about a smooth axis through its centre and perpendicular to the disc. A constant torque is applied to the disc for 3s from rest and the angular velocity at the ned of that time is `(240)/(pi)rev//min` find the magnitude of the torque. if the torque is then removed and the disc is brought to rest in `t` seconds by a constant force of 10 N applied tangentially at a point on the rim of the disc, find `t`
View SolutionA uniform disc of mass `m` and radius `R` I rotated about an axis passing through its centre and perpendicular to its plane with an angular velocity `omega_()`. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficnet of friction between te disc and the surface is `mu`, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View SolutionA solid body rotates about a stationary axis so that the rotation angle `theta` varies with time as `theta=6t-2t^(3)` radian. Find
(a) the angular acceleration at the moment when the body stops and
(b) the average value of angular velocity and angular acceleration averaged over the time interval between `t=0` and the complete stop.
View Solution
A rod of mass `m` and length 2 R is fixed along te diameter of a ring of same mass `m` and radius R as shown in figure. The combined body is rolling without slipping along x-axis find the angular momentum about z-axis.
View Solution
The figure shows a thin ring of mass `M=1kg` and radius `R=0.4m` spinning about a vertical diameter (take `I=(1)/(2)MR^(2))` A small beam of mass `m=0.2kg` can slide without friction along the ring When the bead is at the top of the ring the angular velocity is `5rad//s` What is the angular velocity when the bead slips halfwat to `theta=45^(@)`?
View SolutionA horizontal disc rotating freely about a vertical axis makes 100 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis if the number of revolution per minute is thereby reduced to 90. Calculate the moment of inertia of disc.
View SolutionA man stands at the centre of a circular platform holding his arms extended horizontally with 4 kg block in each hand. He is set rotating about a vertical axis at `0.5rev//s`. The moment of inertia of the man plus platform is `1.6kg-m^(2)`, assumed constant, the block are 90 cm from the axis of rotation. He now pulls the blocks in towards his body until they are 15 cm from the axis of rotation. Find (a) his new angular velocity and (b) the initial and final kinetic energy of the man and platform (c) how much work most the man do to pull int he blocks?
View SolutionA horizontally oriented uniform disc of mass `M` and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass `m`. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity `omega_(0)`. Then by means of a force `F` applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.
View Solution
Consider a cylinder of mass `M` and radius `R` lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.
View Solution
Find the acceleration of the cylinder of mass `m` and radius `R` and that of plank of mass `M` placed on smooth surface if pulled with a force `F` as shown in figure. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.
View SolutionA uniform rod AB of length 2l and mass `m` is rotating in a horizontal plane about a vertical axis through A, with angular velocity `omega`, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
View SolutionA uniform rod of length `L` rests on a frictionless horizontal surface. The rod is pivoted about a fixed frictionless axis at one end. The rod is initially at rest. A bulled travelling parallel to the horizontal surface and perpendicular to the rod with speed `v` strikes the rod at its centre and becomes embedded in it. the mass of the bullet is one-sixth the mass of the rod.
(a). What is the final angular velocity of the rod?
(b). What is the ratio of the kinetic energy of the system after the collision to the kinetic energy of te bullet the o collision?
View SolutionA uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at `60^(@)` to AC.
View Solution
Level 1 Subjective questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions