Complete Solutions to Level 1 Objective of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Level 1 Objective |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
The moment of inertia of a body does not depend on
View SolutionThe radius of gyration of a disc of radius 25 cm about a centroidal axis perpendicular to disc is
View SolutionA shaft initially rotating at 1725 rpm is brought to rest uniformly in 20s. The number of revolutions that the shaft will make during this time is
View SolutionA man standing on a platform holds weights in his outstretched arms. The system is rotated about a central vertical axis. If the man now pulls the weights inwards close to his body then
View SolutionMoment of inertia of a thin semicircular disc `(mass - M & radius = R)` about an axis through point `O` and perpendicular to plane of disc, is given by :
 .
.
View SolutionTwo bodies A and B made of same material have the moment of inertial in the ratio `I_(A):I_(B)=16:18` The ratio of the masses `m_(A):m_(B)` is given by
View SolutionWhen a sphere rolls down an inclined plane, then identity the correct statement related to the work done by friction force.
View SolutionA circular table rotates about a vertical axis with a constant angular speed `omega`. A circular pan rests on the turn table (with the centre coinciding with centre of table) and rotates with the table. The bottom of the pan is covered with a uniform small thick layer of ice placed at centre of pan. The ice starts melting. The angular speed of the turn table.
View SolutionIf `R` is the radius of gyration of a body of mass `M` and radius `r`, then the ratio of its rotational to translational kinetic energy in the rolling condition is
View SolutionA solid sphere rolls down two different inclined planes of the same height but of different inclinations
View SolutionFor the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
View SolutionA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View SolutionA horizontal disc rotates freely with angular velocity `omega` about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partily rolling and partly sliding. During this kind of motion of the sphere.
View SolutionA particle of mass `m=3kg` moves along a straight line `4y-3x=2` where `x` and `y` are in metre, with constant velocity `v=5ms^(-1)` the magnitude of angular momentum about the origin is
View SolutionA solid sphere rolls without slipping on a rough horizontal floor, moving with a speed `v`. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionLer l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with AB. The moment of inertia of the plate about the axis CD is then equal to
View Solution
A spool is pulled horizontally on rough surface by two equal and opposite forces as shown in the figure. Which of the following statements are correct?
View Solution
Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity `omega_(0)` and has rotational kinetic energy `K_(0)`. Change in the rotational kinetic energy of the system is
View SolutionThe moment of inertia of hollow sphere (mass M) of inner radius R and outer radius 2R, having material of uniform density, about a diametric axis is
View SolutionA rod of uniform cross-section of mass `M` and length `L` is hinged about an end to swing freely in a vertical plane. However, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
View Solution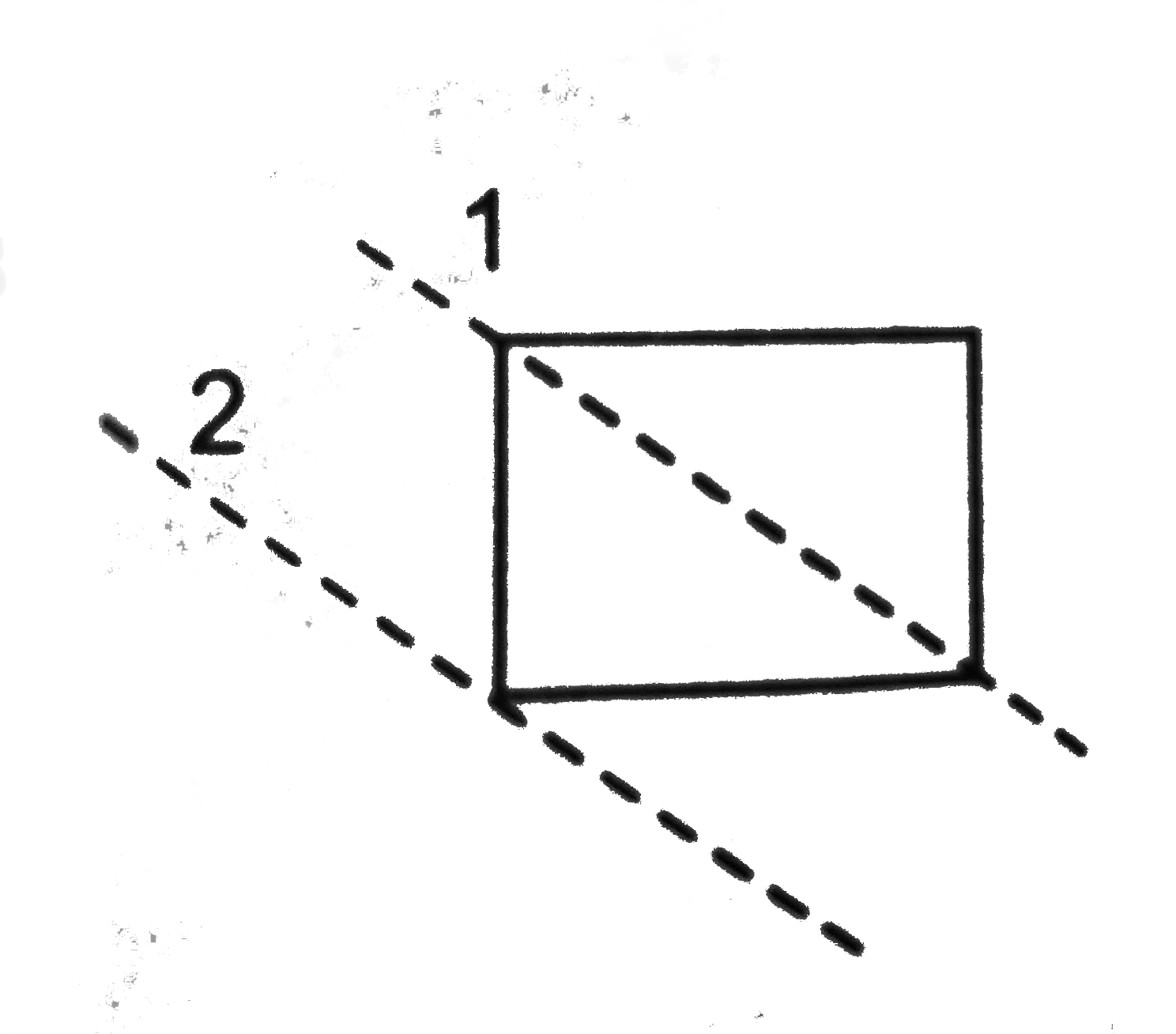
Let `I_(1)` and `I_(2)` be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio `I_(1):I_(2)` is
View SolutionMoment of inertia of a uniform rod of length `L` and mass `M`, about an axis passing through `L//4` from one end and perpendicular to its length is
View Solution
A uniform rod of legth `L` is free to rotate in a vertica plane about a fixed horizontal axis through `B`. The rod begins rotating from rest. The angular velocity `omega` at angle `theta` is given as
View SolutionTwo partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in `kg-m^(2))`
View Solution
Find moment of inertia of a thin sheet of mass `M` in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is `L`
View SolutionA square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one of its corner is

View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View Solution
The figure shows two cones A and B with the conditions `h_(A)lth_(B),rho_(A)gtrho_(B)`
`R_(A)=R_(B)`,`m_(A)=m_(B)`. Identify the correct statement abut their axis of symmetry.
View Solution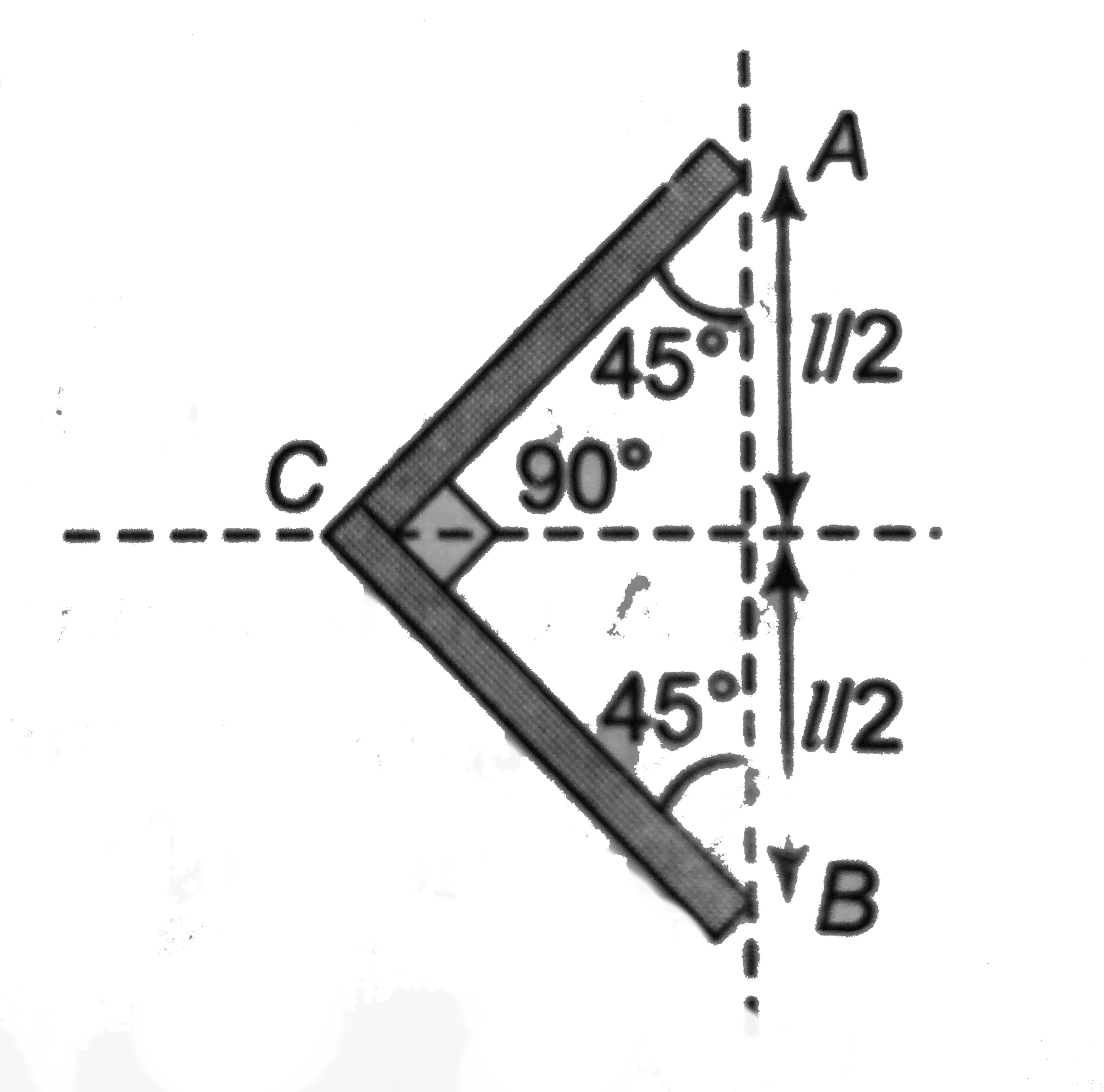
Linear mass density of the two rods system, AC and CD is x. moment of inertia of two rods about an axis passing through AB is
View Solution
Level 1 Objective questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions