Complete Solutions to Solved Examples of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Solved Examples |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
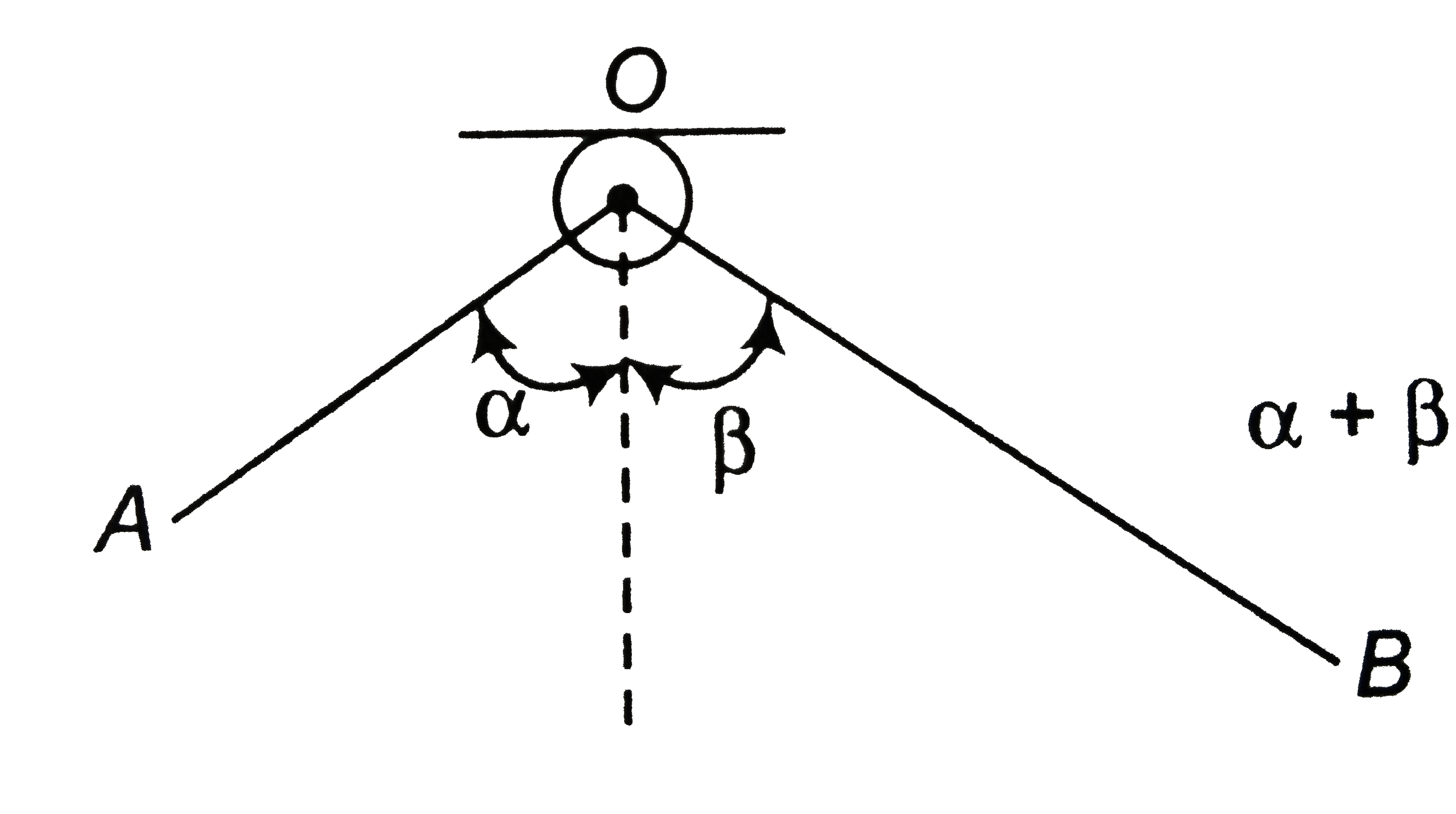
A uniform L shaped rod of mass 3 m is hinged at point O. length OB is two times the length OA. It is in equilibriu.
Find
(a). Relation between `alpha` and `beta`
(b). Net hinge force.
View Solution
A ring of mass `m` is rolling without slipping with linear speed `v` as shown in figure. Four particles each of mass `m` are also attached at points A, B , C and D find total kinetic energy of the system.
View Solution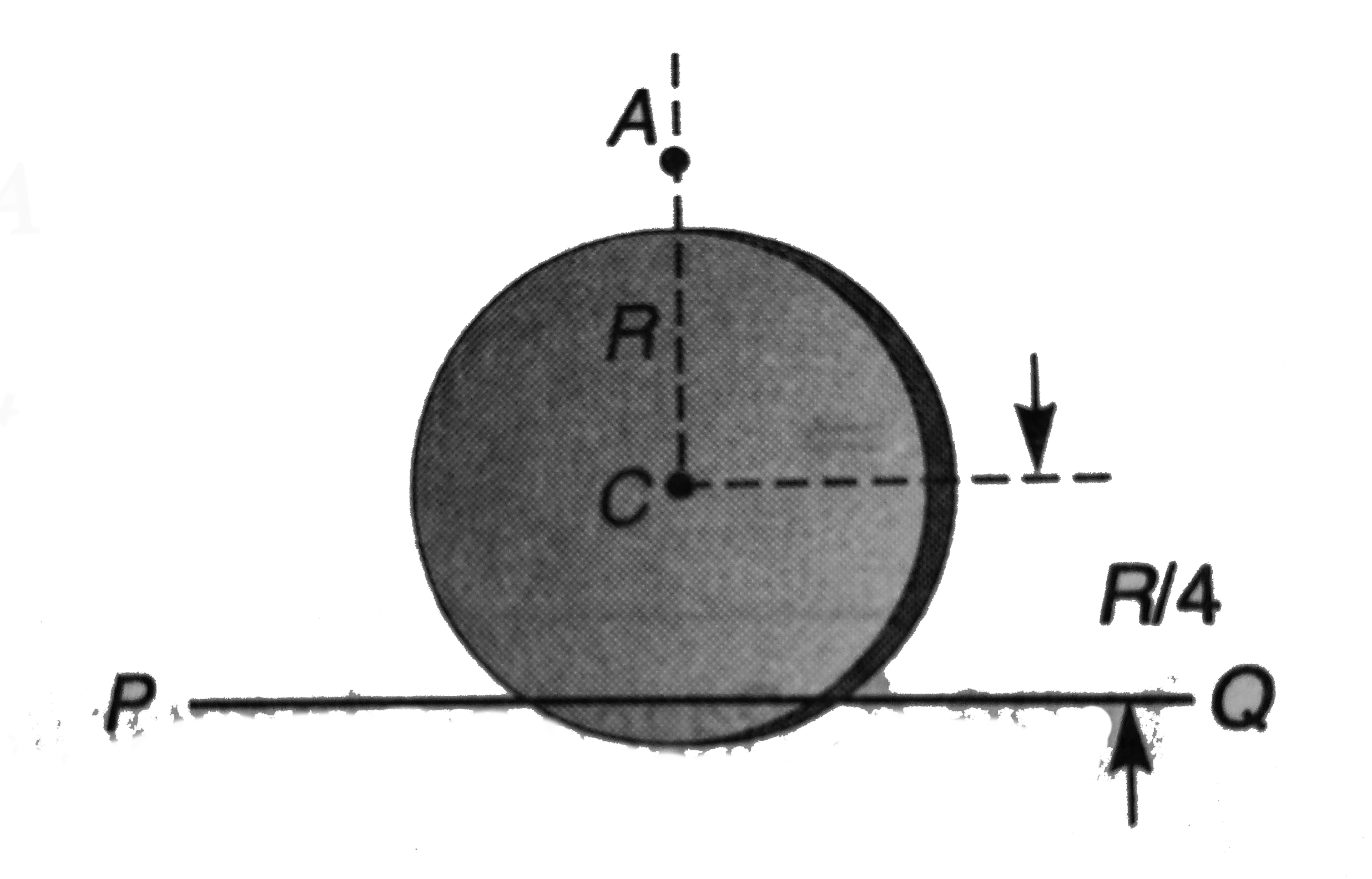
A uniform circular disc has radius `R` and mass `m`. A particle, also of mass `m`, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance `R//4` from the centre `C` of the disc. The line AC is perpendicular to `PQ`. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View Solution
A solid shere of mass `m` and radius `R` is kept over a rough ground. A time varying force `F=2t` is acting at the topmost point as shown in figure.
(a). Find angular momentum of the sphere about the bottommost point as a function of time `t`
(b). Does this result depend on the fact whether the ground is rough or smooth?
View Solution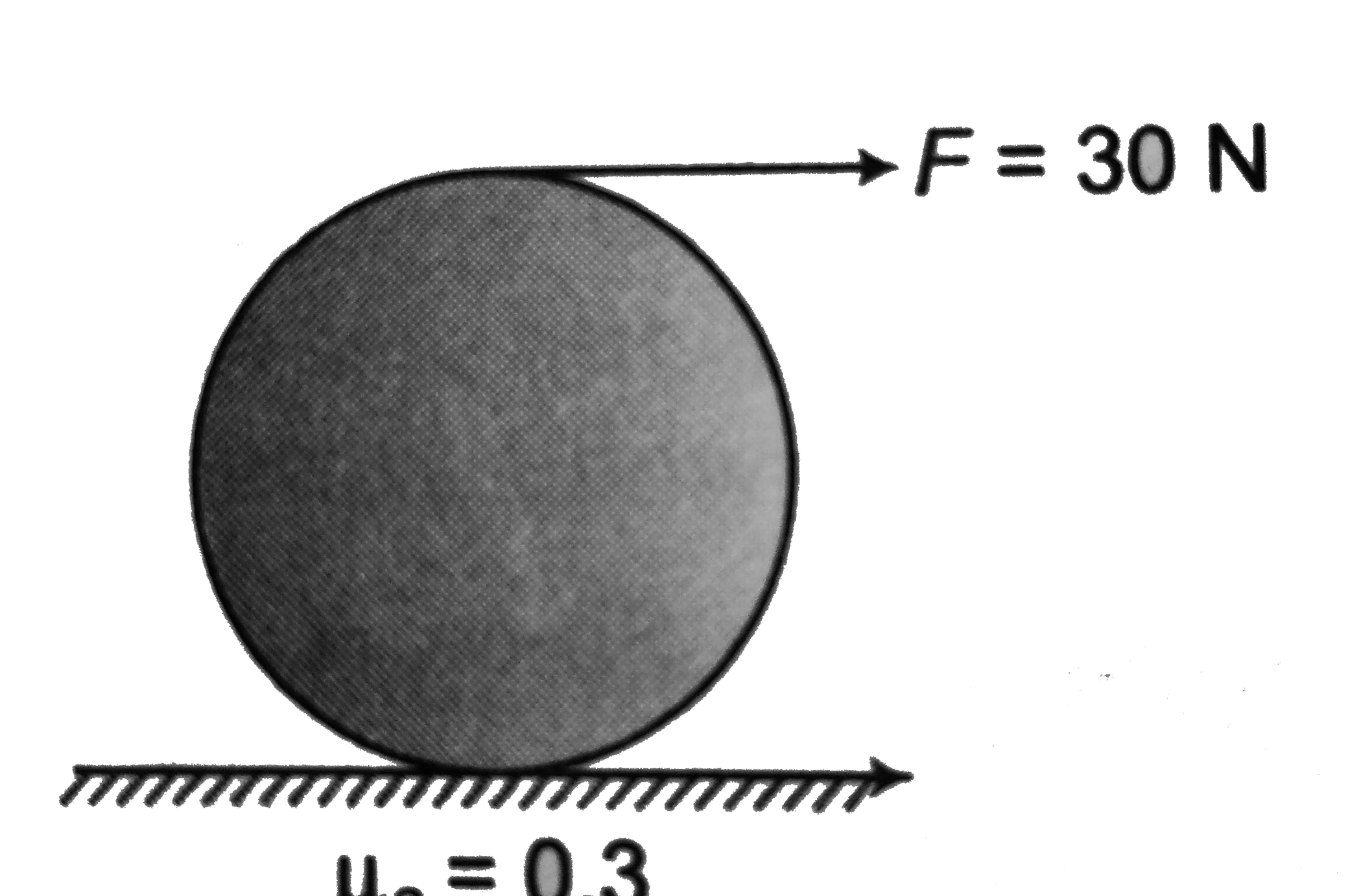
A solid sphere of mass 5 kg and radius `1m` is kept over a rough surface as shown in figure. A force `F=30N` is acting at the topmost point.
(a). Check whether the pure rolling will take place or not
(b). Find direction and magnitude of friction actually acting on the sphere.
(c). Find linear acceleration `a` and angular acceleration `alpha` take `g=10m//s^(2)`
View SolutionRepeat all parts of above problem for `F=40N`
View SolutionA solid cylinder of mass m and radius r starts rolling down an inclined plane of inclination `theta`. Friction is enough to prevent slipping. Find the speed of its centre of mass when its centre of mass has fallen a height `h`.
View Solution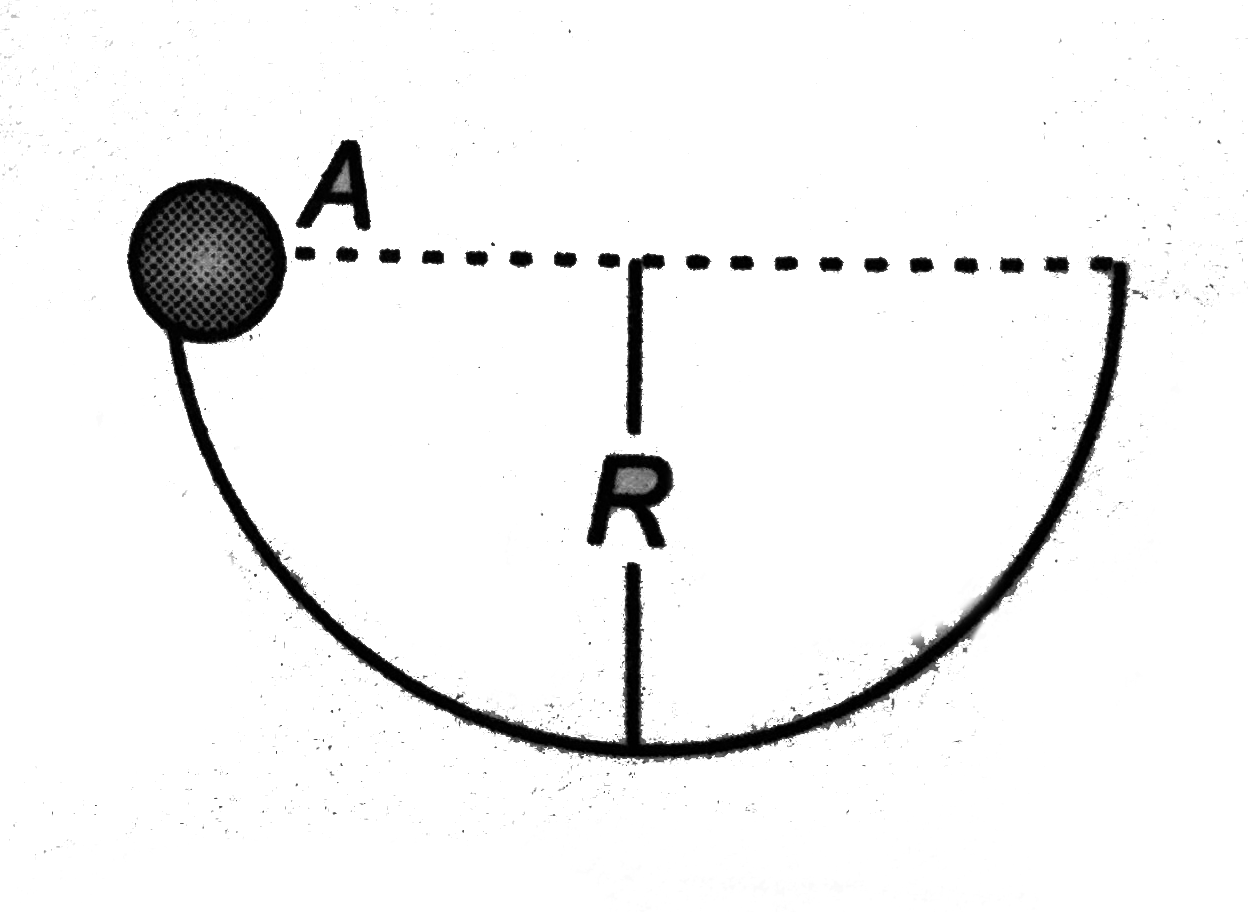
A small solid cylinder of radius `r` is released coaxially from point A inside the fixed large cylindrical bawl of radius R as shown in figure. If the friction between the small and the large cylinder is sufficient enough to prevent any slipping then find.
(a). What fractions of the total energy are translational and rotational when the small cylinder reaches the bottom of the larger one?
(b). The normal force exerted by the small cylinder on the larger one when it is at the bottom.
View Solution
A small object of uniform density rolls up a curved surface with an initial velocity `v`. It reaches up to a maximum height of `(3v^(2))/(4g)` with respect to the initial position. The object is
(a). Ring
(b). solid sphere
(c). hollow sphere
(d). disc
View Solution
A solid ball rolls down a parabolic path `ABC` from a height `h` as shown in figure. Portion `AB` of the path is rough while `BC` is smooth. How high will the ball climb in `BC`?
View Solution
A ball moves over a fixed track as shown in thre figure. From A to B the ball rolls without slipping. If surface BC is frictionless and `K_(A),K_(B)` and `K_(C)` are kinetic energies of the ball at A, B and C respectively then
(a). `h_(A)gth_(C),K_(B)gtK_(C)`
(b). `h_(A)gth_(C),K_(C)gtK_(A)`
(c). `h_(A)=h_(C),K_(B)=K_(C)`
(d). `h_(A)lth_(C),K_(B)gtK_(C)`
View Solution
A small solid sphere of mass `m` is released from point A. portion AB is sufficiently rough (to provide accelerated pure rolling) BC is smooth and after C the ball moves freely under gravity find gravitational potential energy (U), rotational kinetic energy `(K_(R))` ad translational kinetic energy `(K_(T))` at points A, B, C , D and E.
View Solution
A rotating disc moves in the positive direction of the x-axis. Find the equation `y(x)` describing the position of the instantaneous axis of rotation if at the initial moment of the centre `c` of the disc was located at the point O after which it moved with constant velocity v while the disc started rotating counterclockwise with a constant angular acceleration `alhpa`. the initial angular velocity is equal to zero.
View SolutionA uniform thin rod of mass `m` and length `l` is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle `theta` with horizontal.
View Solution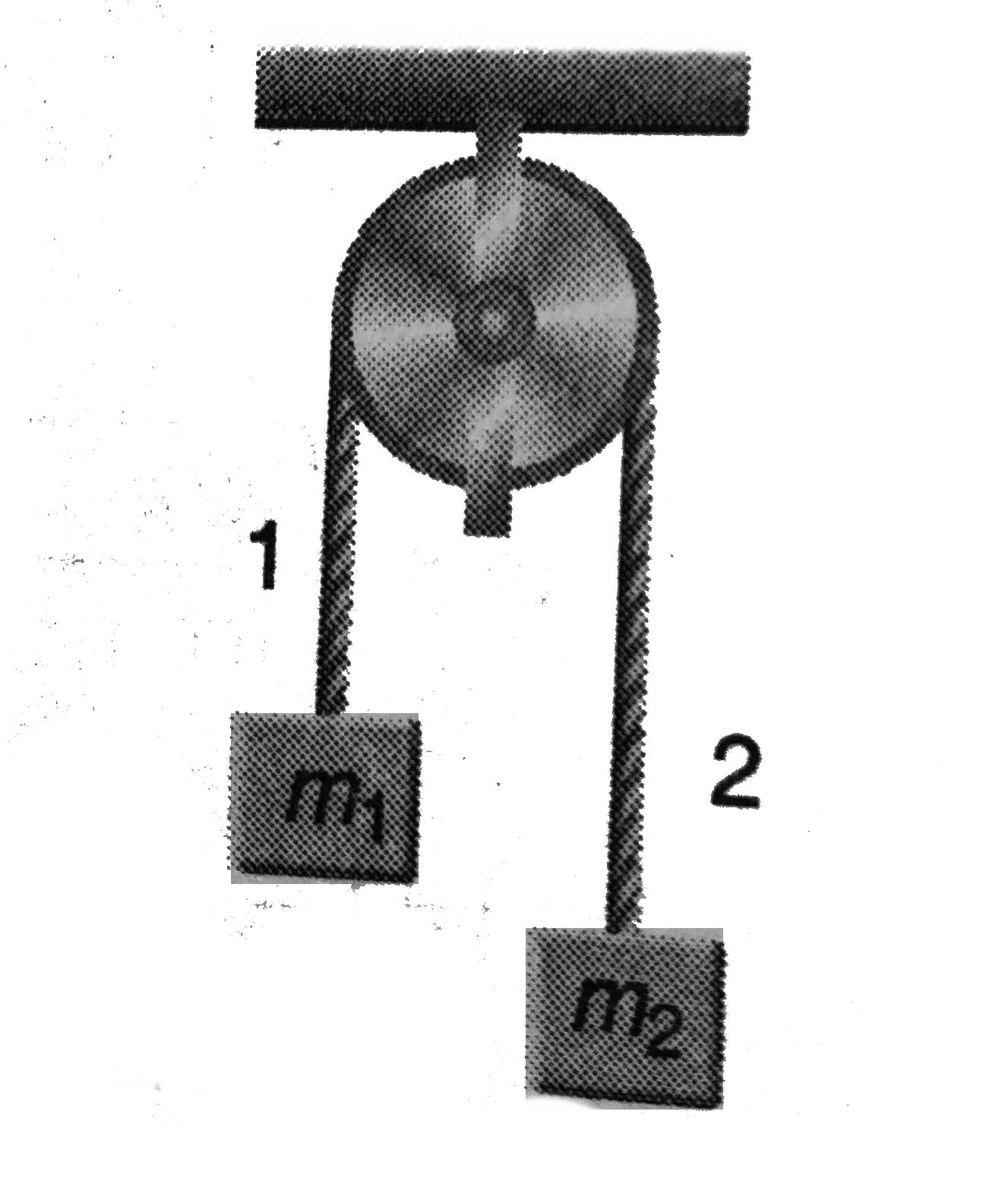
In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius `R` is equal to `m` and the masses of two bodies are equal to `m_(1)` and `m_(2)`. The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions `(T_(1))/(T_(2))` of the vertical sections of the thread in the process of motion.
View Solution
solid sphere of radius `r` is gently placed on a rough horizontal ground with an initial angular speed `omega_(0)` and no linear velocity. If the coefficient of friction is `mu`, find the time `t` when the slipping stops. in addition state the linear velocity `v` and angular velocity `omega` at the end of slipping
View Solution
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance `h` above the centre line as shown in figure. The ball leaves the cue with a speed `v_(0)` and because of its forward english (backward slipping) eventually acquires a final
speed `(9)/(7)v_(0)` show that `h=(4)/(5)R`
Where `R` is the radius of the ball.
View Solution
For the given dimensions shown in figure, find critical value of coefficient of friction `mu`
View SolutionIn the figure shown in the text, if the block is a cube of side `a`
find
(a). `omega` just after impact
(b). Loss of mechanical enegy during impact
(c) minimum value of v so as the block overcomes the obstacle and does not turn back.
View Solution
Consider the arrangement shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a masslessm frictionless pulley to a falling weight, determine the acceleration of the falling mass `m` in terms of only the mass of the cylinder `M`, the mass `m` and `g`
View Solution
A thin massless thread is wound on a reel of mass 3 kg and moment of inertial 0.6 `kg-m^(3)` the hub radius is `R=10`cm and peripheral radius is `2R=20` cm the reel is placed on a rough table and the friction is enough to prevent slipping. find the acceleration of the centre of reel and of hanging mass of 1 kg.
View Solution
A body of mass `m`, radius `R` and moment of inertia `I` (about an axis passing through the centre of mass and perpendicular to plane of motion) is released from rest over a sufficiently rough ground (to provide accelerated pure rolling) find linear acceleration of the body.
View SolutionIn the figure given in the text if mass of the rod is `m` then find hinge force.
(a). Just after the rod is released from the horizontal position.
(b). When rod becomes vertical
View SolutionTwo uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.
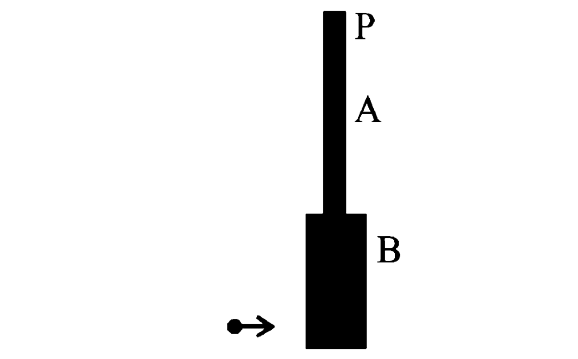
View SolutionA rod AB of mass `M` and length L is lying on a horizontal frictionless surface. A particle of mass `m` travelling along the surface hits the end A of the rod with a velocity `v_(0)` in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio `m//M`
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time `piL//3v_(0)` after the collision.
View Solution
Solved Examples questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions