Complete Solutions to Examples of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| DC PANDEY | Examples |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Three particles of masses 1 g, 2g and 3 g are kept at points (2cm,0), (0.6 cm), (4cm, 3cm) find moment of inertia of all three particles (in gm`-cm(2))` about (a) x-axis
(b). Y-axis
(c). Z-axis.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.
View Solution
Find the moment of inertia of a solid sphere of mass `M` and radias `R` about an axis XX shown in figure.
View SolutionConsider a uniform rod of mass m and length 2l with two particles of mass `m` each at its ends. Let AB be a line perpendicular to the length of rod and passig through its centre. Find the moment of inertial of the system about AB.
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View Solution
Rod AB has length L. velocity of end A of the rod has velocity `upsilon_(0)` at the given instant.
(a). Which type of motion the rod has?
(b). Find velocity of end B at the given instant.
(C). Find the angular velocity of the rod.
View SolutionFind the torque of a force `F=a(hati+2hatj+3hatk)` `N` about a point O. The position vector of point of application of force about `O` is `r=(2hati+3hatj-hatk)` `m`.
View SolutionA small ball of mass 1.0 kg is attached to one end of a 1.0 m long massless string and te other end of the string is hung from a point `O`. When the resulting pendulum is making `30^(@)C` from the vertical, what is the magnitude of net torque about the point of suspension? [Take `g=10m//s^(2)`]
View SolutionA force `F=(2hati+3hatj+4hatk)N` is acting at point `P(2m,-3m,6m)` find torque of this force about a point `O` whose position vector is
`(2hati-5hatj+3hatk)` m.
View SolutionA solid sphere of mass 2 kg and radius 1 m is free to rotate about an axis passing through its centre. Find a constant tangential force `F` requird to rotate the sphere I that tim interval.
View SolutionA angular positio of a point on the rim of a rotating wheel is given by `theta=4t-3t^(2)+t^(3)` where `theta` is in radiuans and `t` is in seconds. What are the angualr velocities at
(a).`t=2.0` and
(b). `t=4.0s`
(c). What is the average angular acceleration for the time interval that begins at `t=2.0s` and ends at `t=4.0s`?
(d). What are the instantaneous angular acceleration at the biginning and the end of this time interval?
View Solution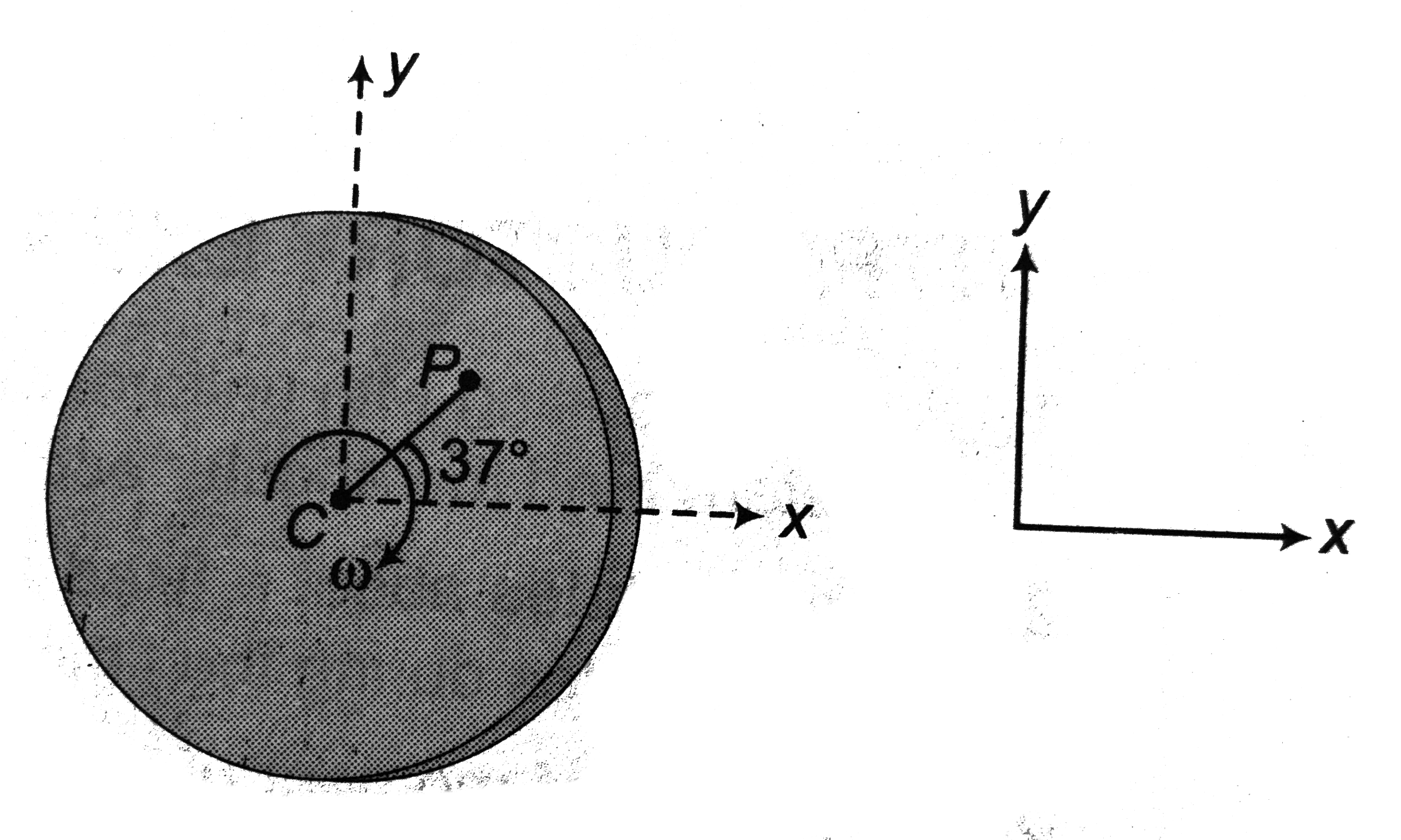
A circular disc is rotating with an angular speed (in radian per sec)
`omega=2t^(2)`
given, `CP=2m`
In terms of `hati,hatj` and `hatk` at `t=1s`
find,
(a). `omega`
(b). `alpha`
(c). linear velocity of the particle lying at `P` (d). linear acceleration of the particle lying `P`
View SolutionA particle of mass `m` is moving along the line `y=b,z=0` with constnat speed `v`. State whether the angular momentum of particle about origin is increasing. Decreasing or constant.
View SolutionA particle of mass `m` is projected from origin `O` with speed `u` at an angle `theta` with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time `t` about `O` before the particle strkes the ground again.
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end `O` wth an angular velocity `omega=4rad//s`. Find angular momentum of the rod about the axis rotation.
View Solution
A cicular disc of mass `m` and radius `R` is set into motion on a horizontal floor with a linear speed `v` in the forward direction and an angular speed `omega=(v)/(R)` in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point `O` of the disc.
View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed `omega`. It picks up a stationary particle of mass `m` at its edge. Find the new angular speed of the wheel.
View Solution
In the figure shown `upsilon=2m//s` `omega=5rad//s` and `CP=1m`
In terms of `hati` and `hatj` find linear velocity of particle P.
View Solution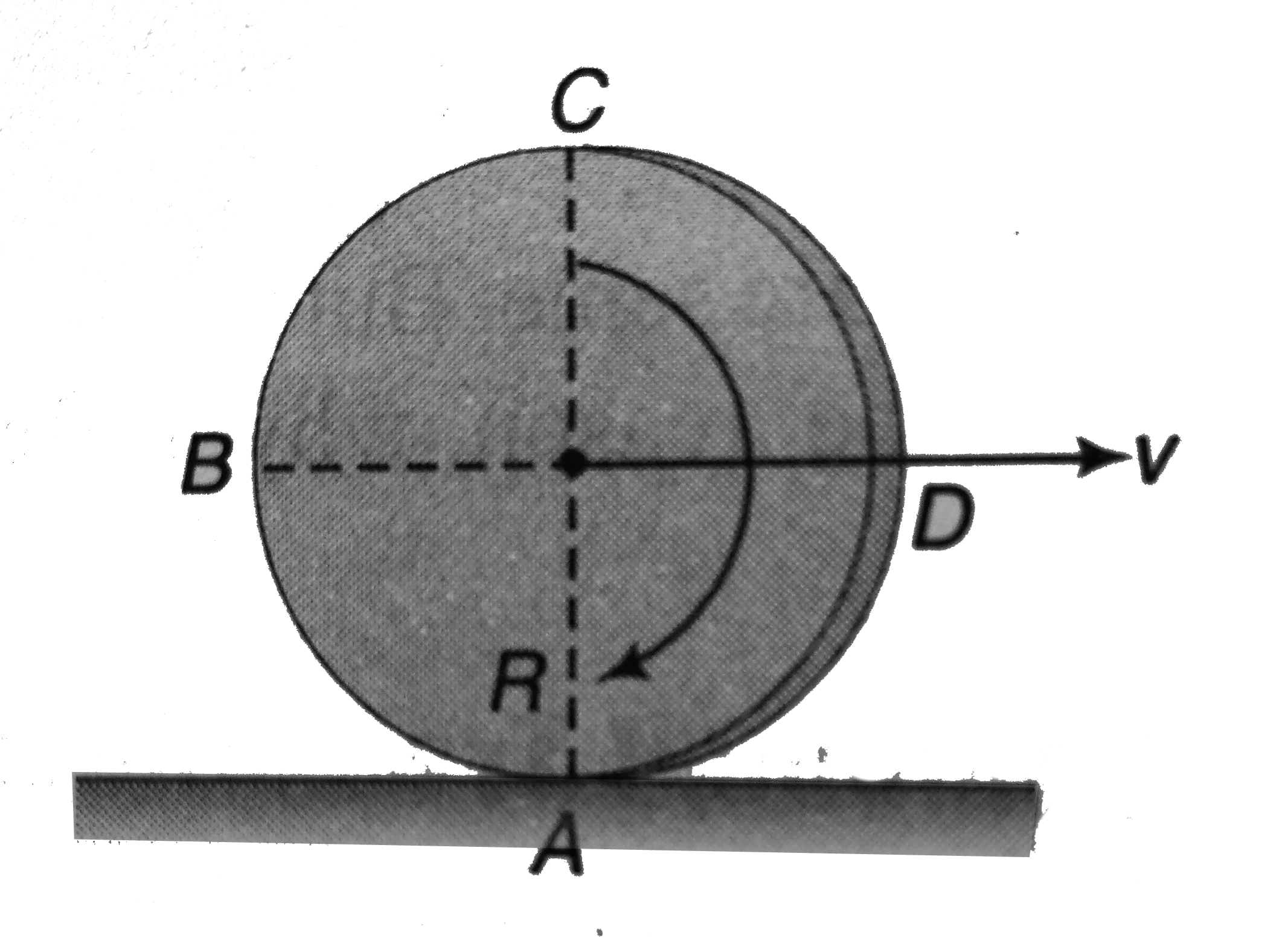
A disc of radius `R` has linear velocity `v` and angular velocity `omega` as shown in the figure. Given `upsilon=romega` find velocity of point A, B, C and D on the disc.
View Solution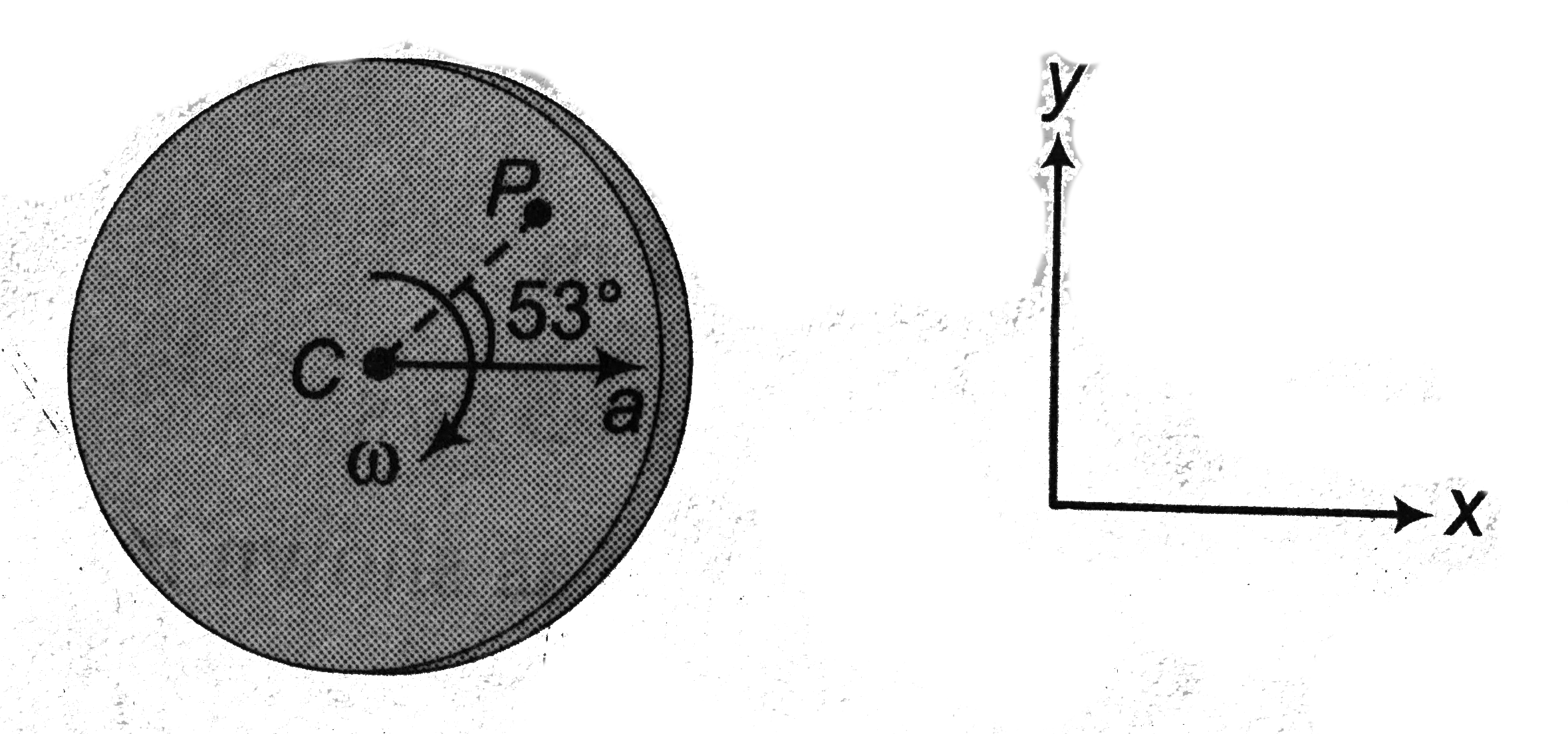
In the shown figure,
`a=2m//s^(2),omega=(2t)rods^(-1)` and `CP=1m`
In terms of `hati` and `hatj`, find linear acceleration of the particle at `P` at `P` at `t=1` s
View Solution
A solid disc is rolling without slipping on a horizontal ground as shown in figure. Its total kinetic energy is 100 J. what is its translational and rotational kinetic energy?
View Solution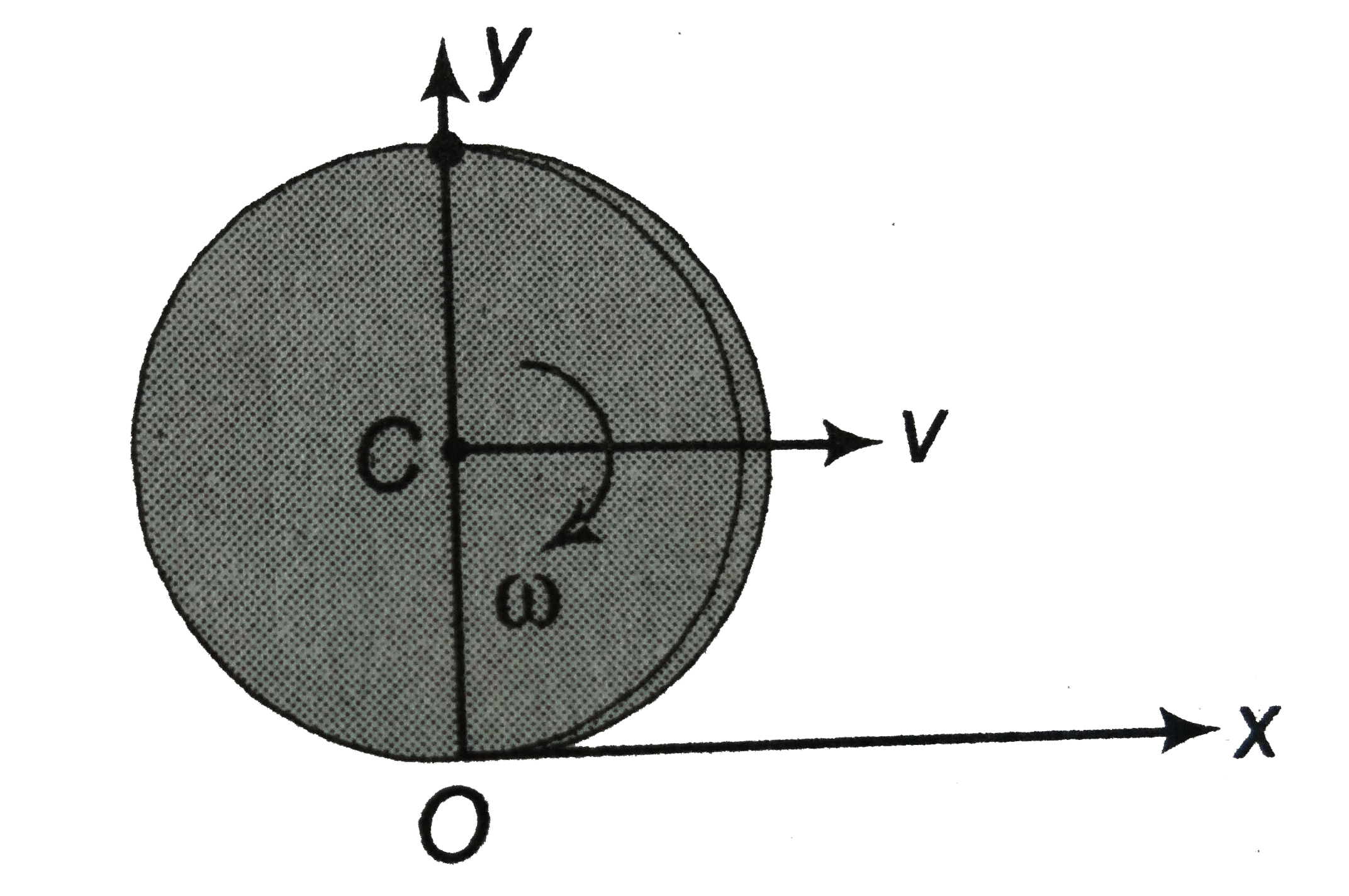
A disc of radius R starts at time `t=0` moving along the positive x-axis with linear speed `v` and angular speed `omega`. Find the x and y coordinates of the bottom most poitn at any time `t`.
View Solution
Using the concept of instantaneous axis of rotation. Find speed of particle P as shown in figure, under pure rolling condition.
View Solution
A disc is rolling (without slipping) on a horizontal surface. C is its centre and Q and P are two point equidistanec from C. let `upsilon_(p),upsilon_(Q)` and `upsilon_(C)` be the magnitude of velocities of points P, Q, and C repsectively,
(a). `upsilon_(Q)gtupsilon_(C)gtupsilon_(P)`
(b). `upsilon_(Q)ltupsilon_(C)ltupsilon_(P)`
(c). `upsilon_(Q)=upsilon_(P),upsilon_(C)=(1)/(2)upsilon_(P)`
(d). `upsilon_(Q)ltupsilon_(C)gtupsilon_(P)`
View Solution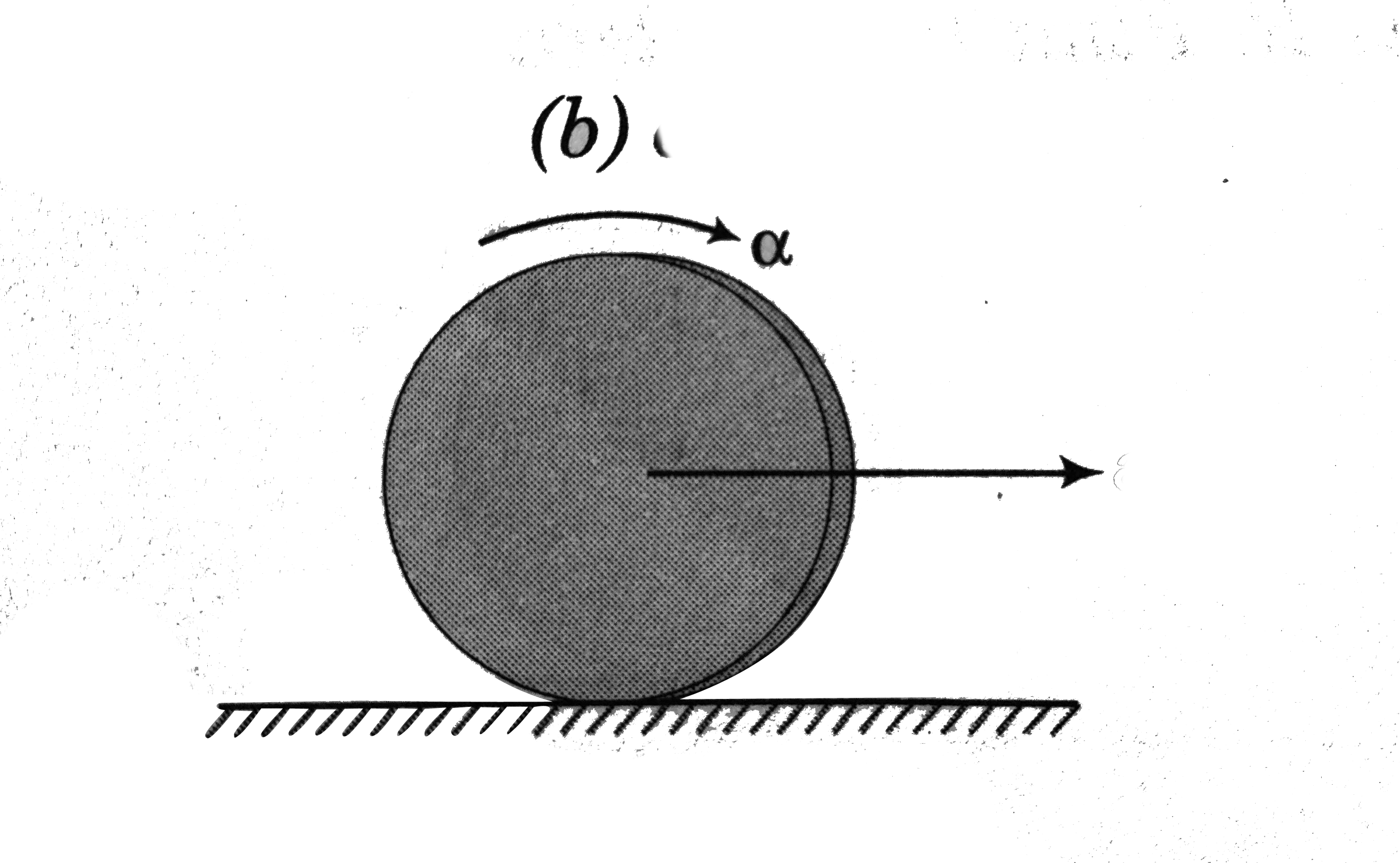
In the shown figure, accelearated pure rolling with takes place, if `a=Ralpha`, find the case if.
(a). `agtRalpha`
(b). `alphaltRalpha`
View SolutionIf accelerated pure rolling is taking place on a stationary ground, then work done by friction is always zero, comment on this.
View Solution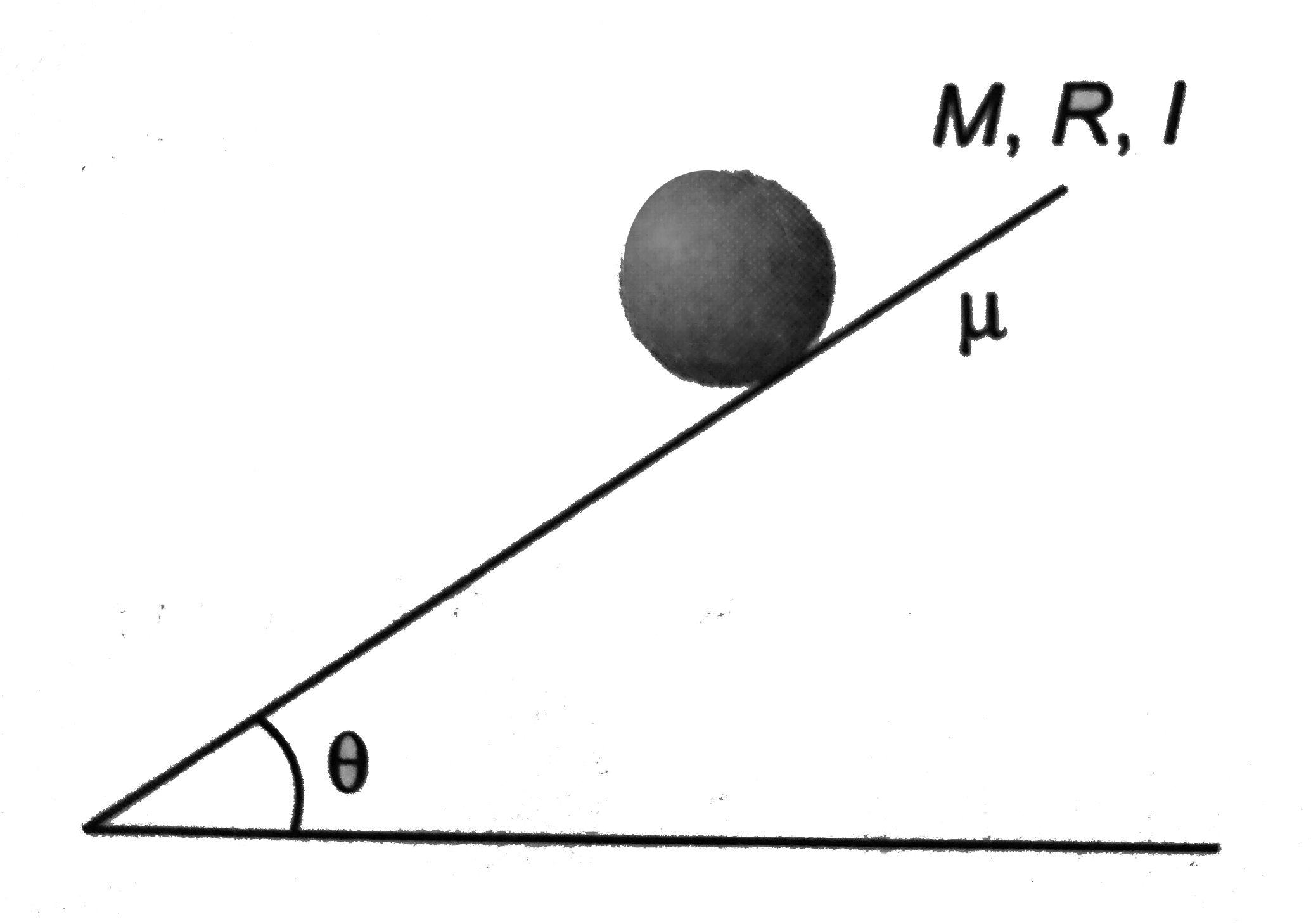
In the shown figure, `M` is mass of the body, `R` its radius an `I` the moment of inertial about an axis passing through centre. Find force of friction `f` acting on the body (upwards), its linear acceleration `a` (down the plane) and type of motion if:
(a) `mu=0`
(b). `multmu_(min)`
(c). `mugtmu_(min)`
Where `mu_(min)` is the minimum value of coefficient of friction required for pure rolling
View Solution
A tangential force `F` acts at the top of a thin spherical shell of mass `m` and radius `R`. Find the acceleration of the shell if it rolls without slipping.
View SolutionA horizontal force `F` acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is `mu`. What is maximum value of `F` for which there is no slipping?
View Solution
A solid sphere of mass `M` and radius `R` is hit by a cue at a height `h` above the centre C. for what value of `h` the sphere will rool without slipping ?
View SolutionA uniform sphere of mass `m` and radius R start rolling without slipping down an inclined plane. Find the time dependence of the angular. How will the result be affected in the case of a perfectly smooth inclined plane? The angle of inclination of the plane is `theta`.
View SolutionA uniform cube of side a and mass `m` rests on a rough horizontal table. A horizontal force `F` is applied normal to one of the faces at a point directly above the centre of the face, at a height `(3a)/(4)` above the base. What is the minimum value of `F` for which the cube begins to tip about an edge?
View SolutionA uniform cylinder of height `h` and radius `r` is placed with its circular face on a rough inclined plane and the inclination of the plane to the horizontal is gradually increased. If `mu` is the coefficient of friction, then under what condition the cylinder will (a) slide before toppling (b) topple before sliding.
View Solution
Examples questions and complete solutions for chapter ROTATIONAL MECHANICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS ROTATIONAL MECHANICS
- Assertion And Reason
- Examples
- Exercise 12.1
- Exercise 12.10
- Exercise 12.11
- Exercise 12.2
- Exercise 12.3
- Exercise 12.4
- Exercise 12.5
- Exercise 12.6
- Exercise 12.7
- Exercise 12.8
- Exercise 12.9
- Level 1 Objective
- Level 1 Subjective
- Level 2
- Level 2 Multiple Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- Solved Example
- Solved Examples
- Subjective Questions