Complete Solutions to All Questions of chapter MOTION IN TWO AND THREE DIMENSIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN TWO AND THREE DIMENSIONS |
| GRB PUBLICATION | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A particle moves so that its coordinates vary with time as x=`alpha sin omegat,y=alpha cos omegat` and `z=bt^(2)`. Find the initial:
(a) position (b) velocity (c) acceleration of the particle.04:08View SolutionThe position of a particle is given as
`vecr=at hati+bt^(2)hatj`
Find the equation of trajectory of the particle.01:34View SolutionA ball is projected horizontally in air such that it moves with a constnat horizontal accelration a due to air flow. Taking the gravitational acelration into account. Find the (a) velocity (b) accelration as the function of time till it strikes the ground.
02:32View SolutionAn aeroplane is flying at a constant height of 1960 m with speed `600 kmh^(-1)` above the ground towards point directly over a person struggling in flood water. At what angle of sight with the vertical should be pilot release a survival kit if it is to reach the person in water ? `(g = 9.8 ms^(-2))`
05:09View SolutionAt anchored enemy ship is at a distance `180 sqrt(3) m` form the security cannon having a muzzle velocity of `60 m//s`.
(a) To what angle must the cannon be elevated to hit the ship.
(b) What is the time of flight.
(c ) How far should the ship be moved away from its initial position so that it becomes beyond the range of the cannon `(g = 10m//s^(2))`.05:12View SolutionDuring volcanic eruption chunks of slid rock are blasted out of the volcano . (a) At what initial speed
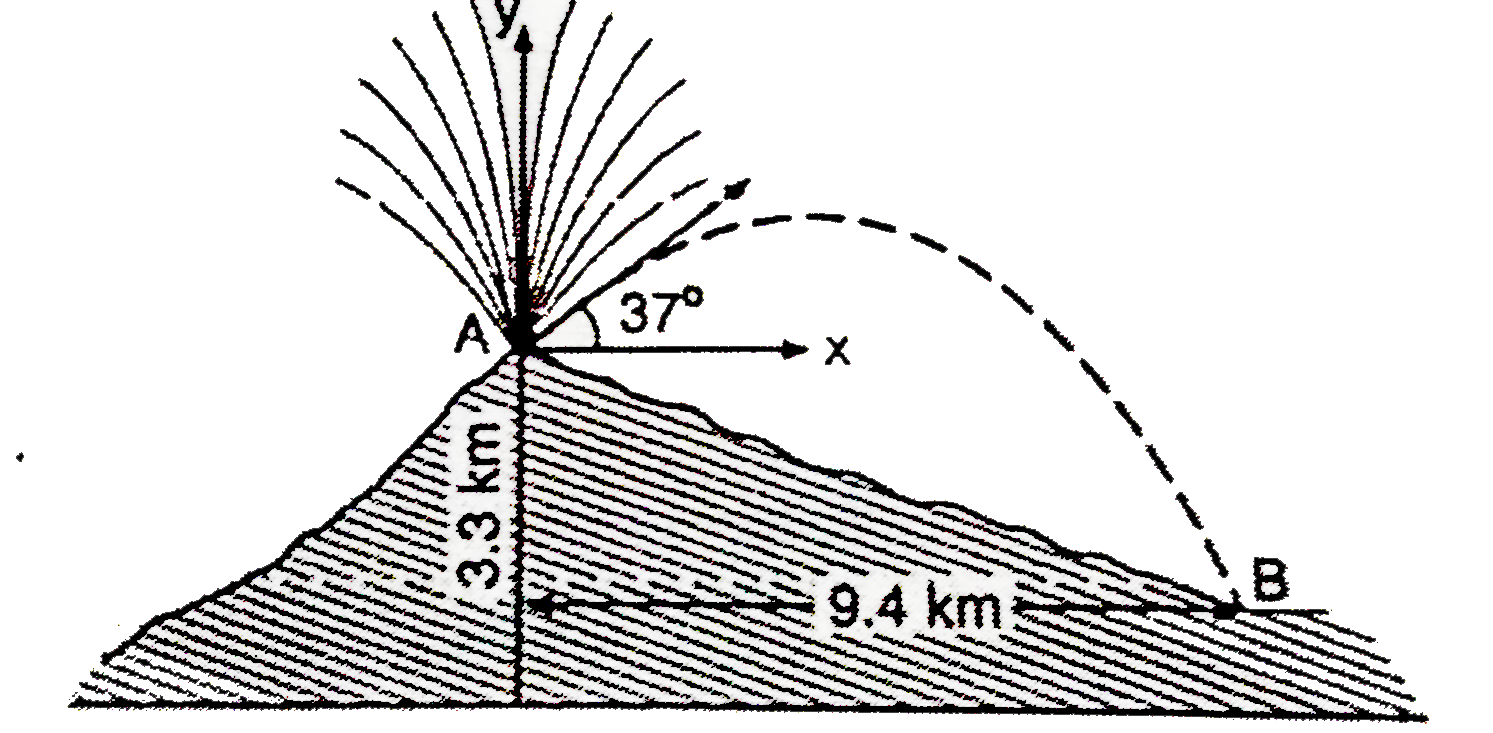
Wou ld a valcanic object have to be ejected at `37^(@)` to the horizontal from the vent A in order to fall at B as shown in Fig. 5.22? (b) what is the time of flight? (g=9.8`m//s^(2)`)06:18View SolutionA gun kept on a striaght horizontal is used to hit a car, traveling along the same road away form the gun with a unfrom speed `20 m//s`. The car is at a distance 0f `160 m` from the gun, when the gun is fired at an angle of `45^(@)` with the horizontal Find the distance of the car from the gun when the shell hits it and the speed of projection of the shell from the gun.
07:51View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If `alpha and beta` be the base angles and `theta` the angle of projection, prove that `tan theta = tan alpha + tan beta` .
02:45View SolutionA gun is fired from a moving platform and the ranges of theshot are observed to be R and S when platform is moving forward or backward respectively with velocity v prove that the elevation of the gun is
`tan ^(-1)[(g(R-S)^(2))/(4V^(2)(R+S))]`06:38View SolutionA rider on an open platform, which is descending at constant speed of 3 ms `s^(-1)`, throws a ball. Relative to platform, ball's initial velocity is horizontal at 12 m/s. The ground is 10m below the location where the ball is thrown:
(i) Where does the ball kit the ground?
(ii) How long after the ball hits the ground does the platform reach grond level?
(iii) With what velocity does the ball hit the ground?03:41View SolutionA block of ice starts sliding down from the top of the inclined roof of a house (angle of inclination of roof=`30^(@)` with the horizontal) along aline of maximum slope. The highest and lowest points of the roof are at heights of 8.1m and 5.6 m respectively from the ground. At what horizontal distance from the starting point will the block hit the ground? Neglect friction.
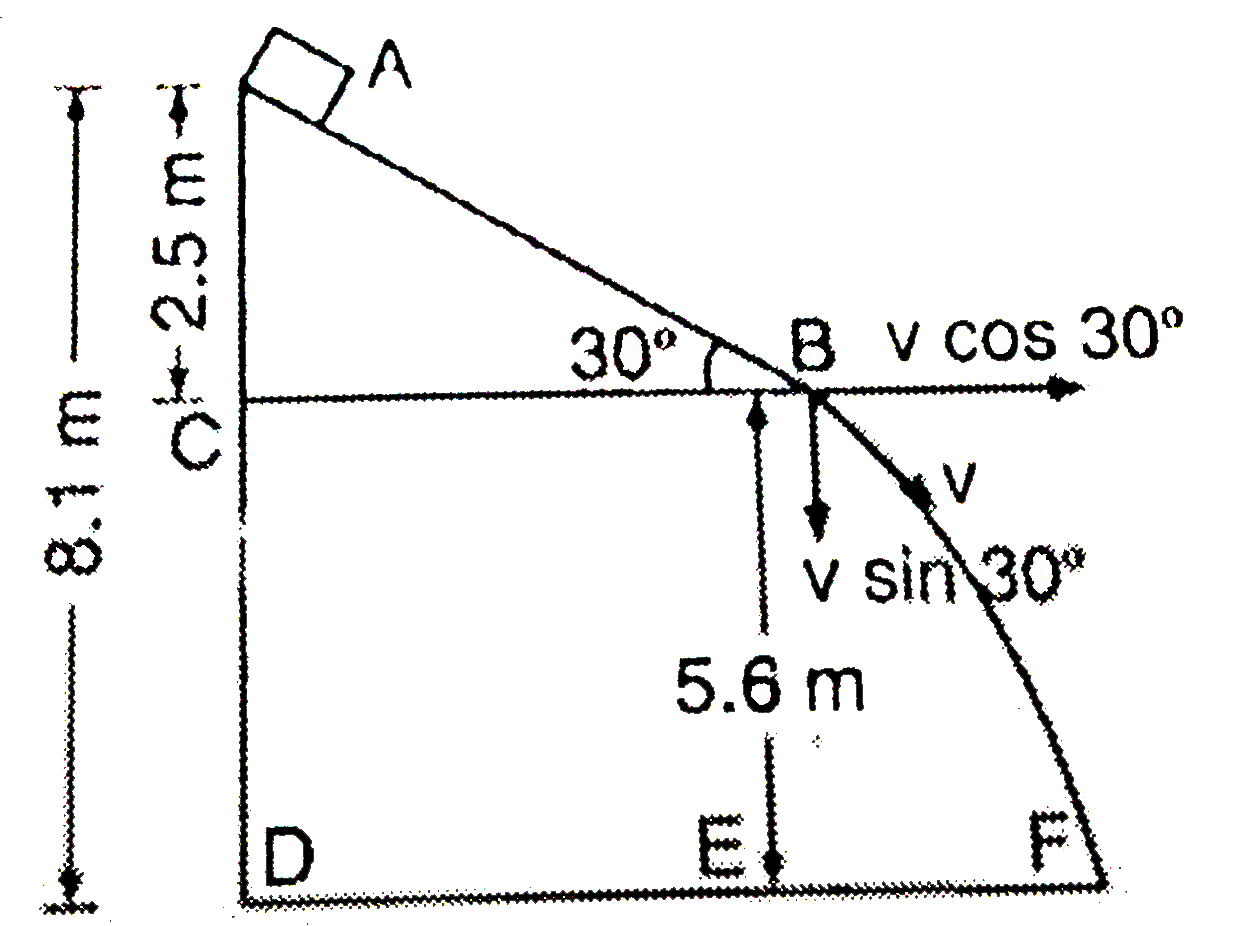 03:35View Solution
03:35View SolutionA stone is projected at an angle `alpha` to the horizontal from the top of a tower of height 3h. If the stone reaches a maximum height 'h', above the tower, show that it reaches the ground at a distance 6h cot `alpha` from the foot of the lower.
01:49View SolutionA jet plane files horizonally at a height h at a speed v. An anti-aircraft gun fires a shell at the plane when it is
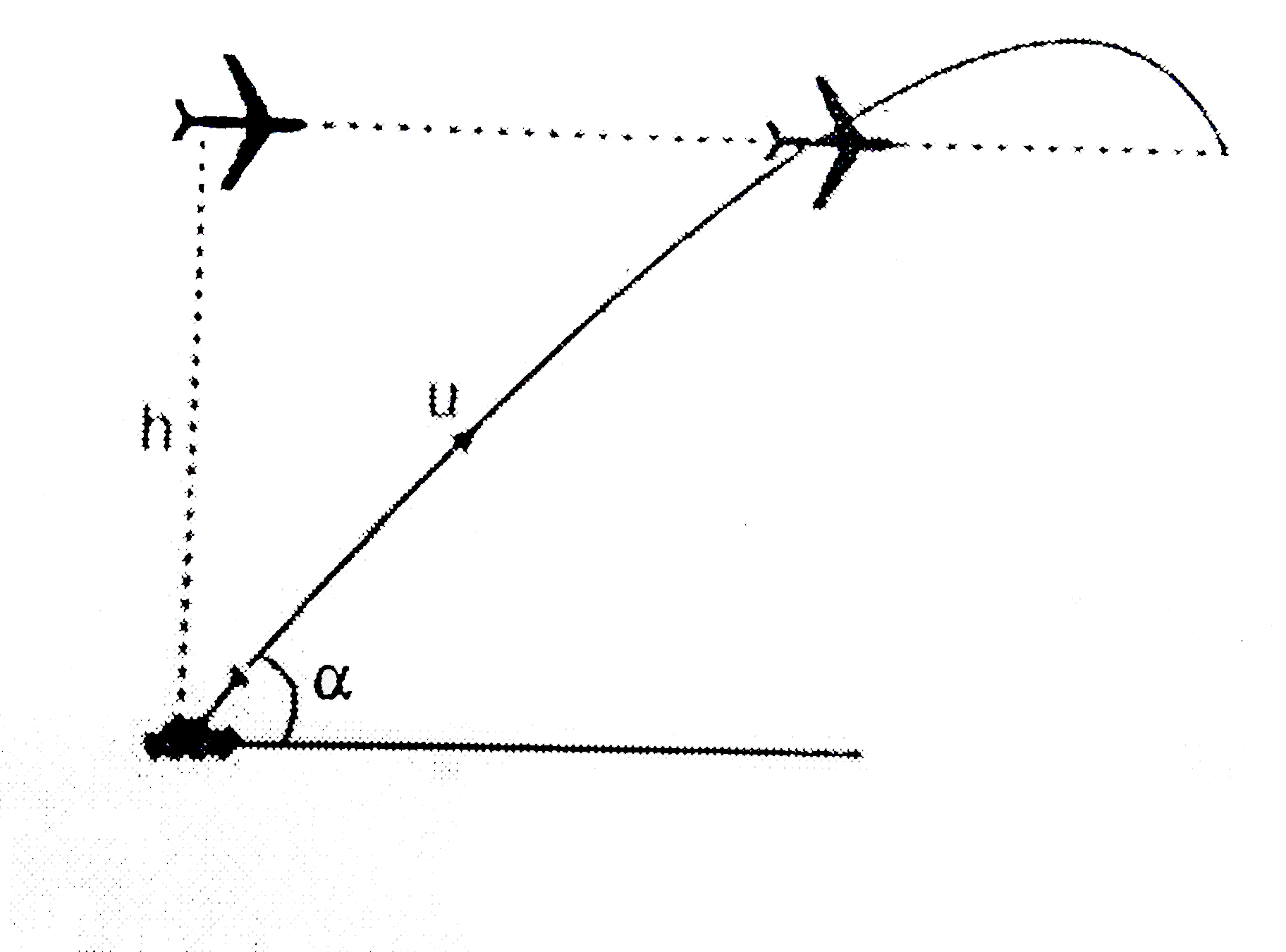
vertically above the gun. Show that the minimum muzzle speed required to hit the plane is `sqrt(v^(2)+2gh)` at an angle `tan^(-1)sqrt(2gh)/(v)`05:13View SolutionA man standing on a hill top projects a stone horizontally with speed `v_0` as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.
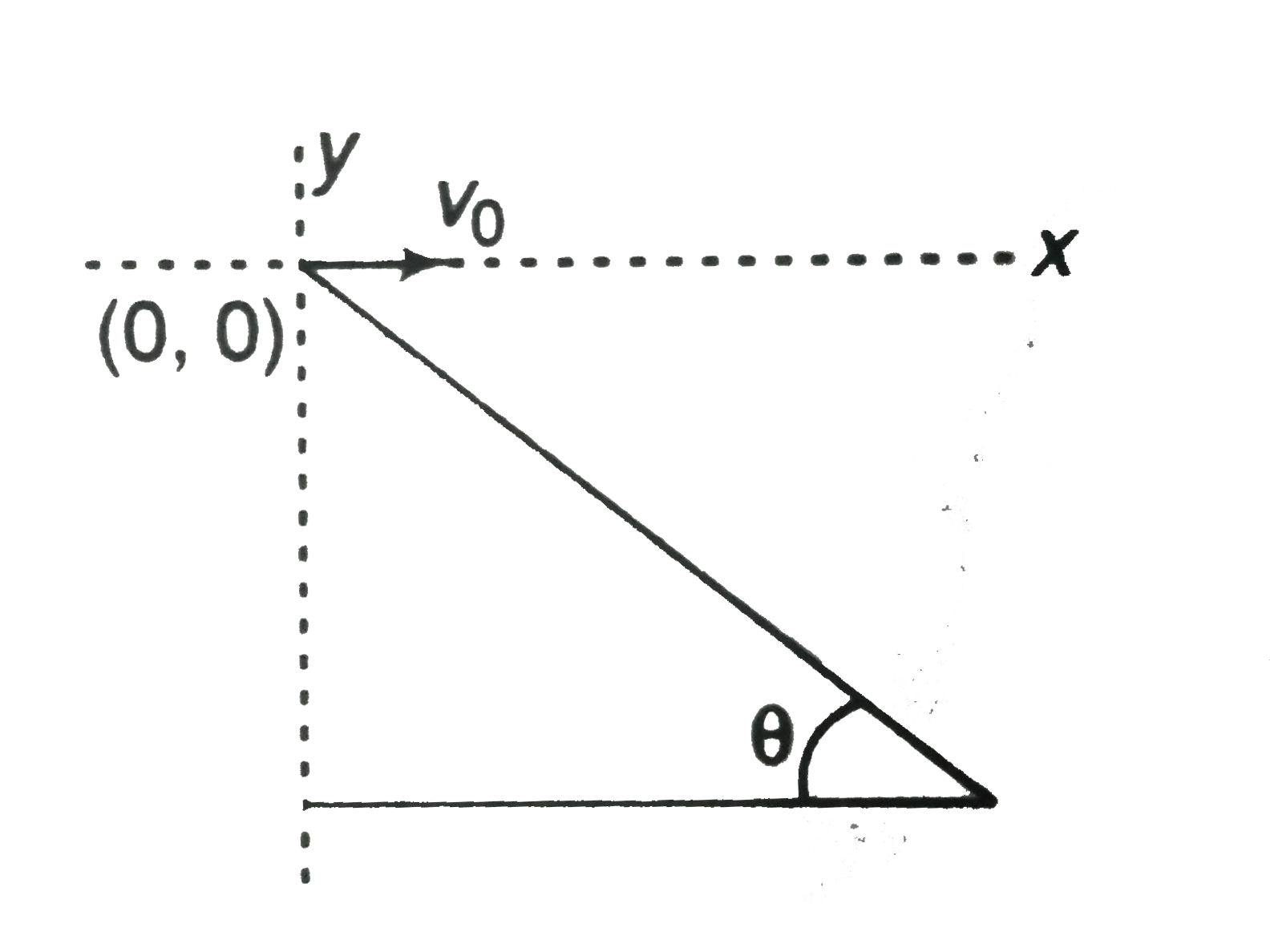 05:35View Solution
05:35View SolutionTwo inclined planes OA and OB having inclinations `30^@` and `60^@` with the horizontal respectively intersect each other at O, as shown in figure. A particle is projected from point P with velocity `u=10 sqrt(3) m//s` along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q. Calculate.
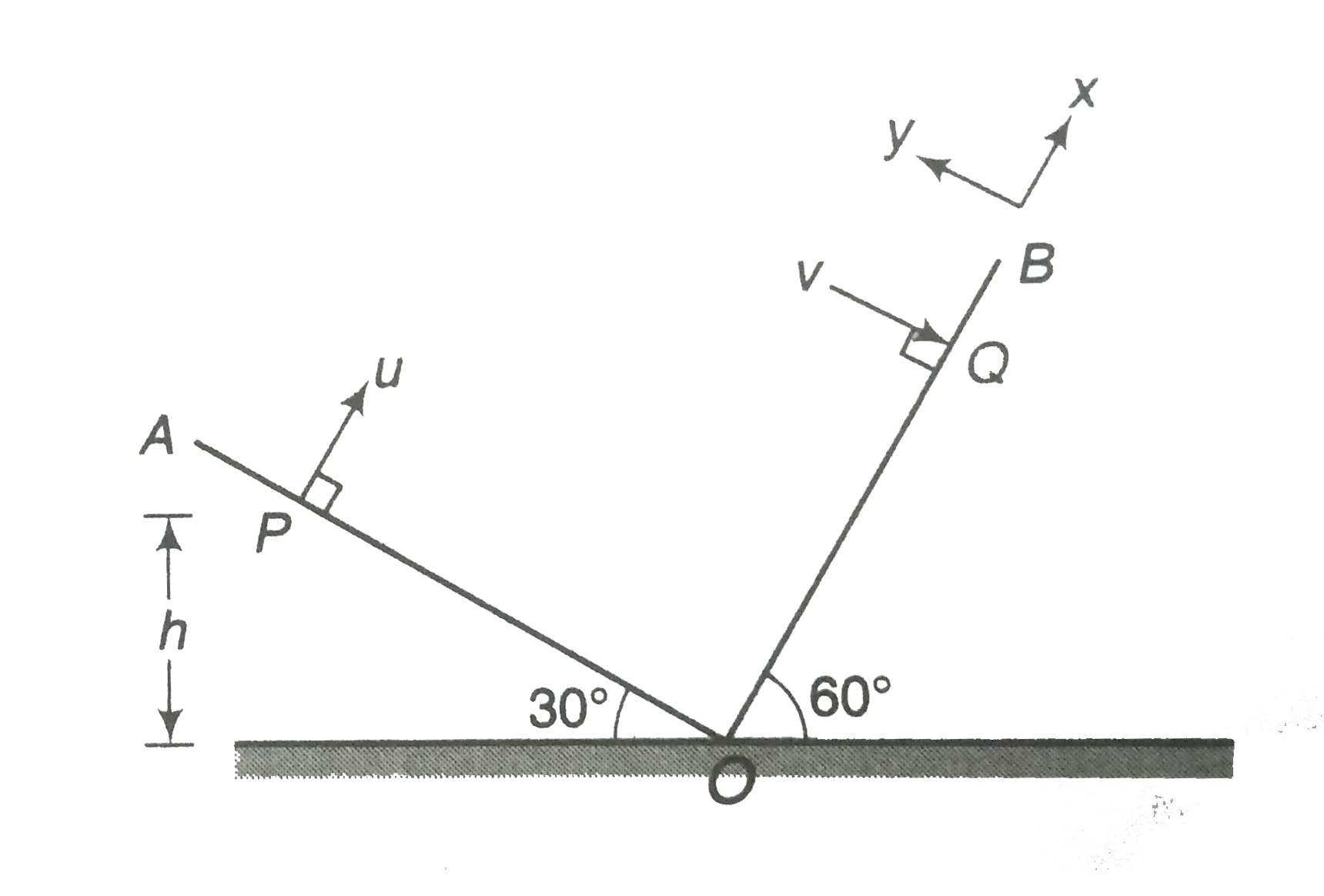
(a) time of flight,
(b) velocity with which the particle strikes the plane OB,
(c) height h of point P from point O,
(d) distance PQ. (Take `g=10m//s^(2)`)06:12View SolutionA man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?07:25View SolutionTwo swimmers start at the same time from point A one bank of a river to reach point B on the other bank, lying directly oppostie to point A. one of them crosses the river along the straight line AB, while the other swims at right angles to the stream and then walks the distance, which he has been carried awayby the stream to get to point B. Both swimmers reach point B at the same time. what was the velocity (assumed uniform) of his walking if velocity of both the swimmers in still water is 2.5 km `h^(-1)` and the stream velocity is 2 km `h^(-1)`?
 03:03View Solution
03:03View SolutionAn aircraft flies at `400 km//h` in still air. A wind of `200sqrt2 km//h` is blowing from the south towards north. The pilot wishes to travel from A to a point B north east of A. Find the direction he must steer and time of his journey if `AB=1000 km.`
10:20View SolutionTo a man walking at the rate of `3 km//h` the rain appear to fall vetically douwnwards. When he increases his speed `6 km//h` it appears to meet him at an angle of `45^@` with vertically. Find the speed of rain.
03:51View SolutionThree insects A,B and C are situated at the vertices of an equillateral triangle of side 1. the insect A heads towards B,B towards C,C towards A with constant speeds v such that they always remain at the vertices of an equilateral triangle. Find the (a) time of their meeting (b) equation of path traced by one insect relative to the other.
04:29View SolutionTwo guns situated at the top of a hill of height `10 m` fire one shot each with the same speed `5sqrt(3) m//s` at some interval of time. One gun fires horizontal and the other fores upwards at an angle of `60^(@)` with the horizontal. Two shots collide in air at a poit `P`. Find (i) time-interval between the firing and (ii) coordinates of the point `P`. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the `x-y` plane.
11:57View SolutionParticles P and Q of mass 20g and 40g respectively are simu ltaneously proejected from points A and B on the ground. The initial velocities of P and Q make `45^(@)` and `135^(@)` angles respectivley with the horizontal AB as shown in the Fig. 5.44 Each particle has an initial speed of 49m/s . the separation AB is 249m. both particles travel in the same vertical plane and undergo a collision. After collision P retraces its path. Determine the position of q when it hits the grou.d How much time after the collision does the particle Q take to reach the ground? (Take g`=9.8m//s^(2)`)
 03:04View Solution
03:04View SolutionTwo towers AB and CD are situated a distance d apart as shown in Fig. 5.45. AB is 20m high and
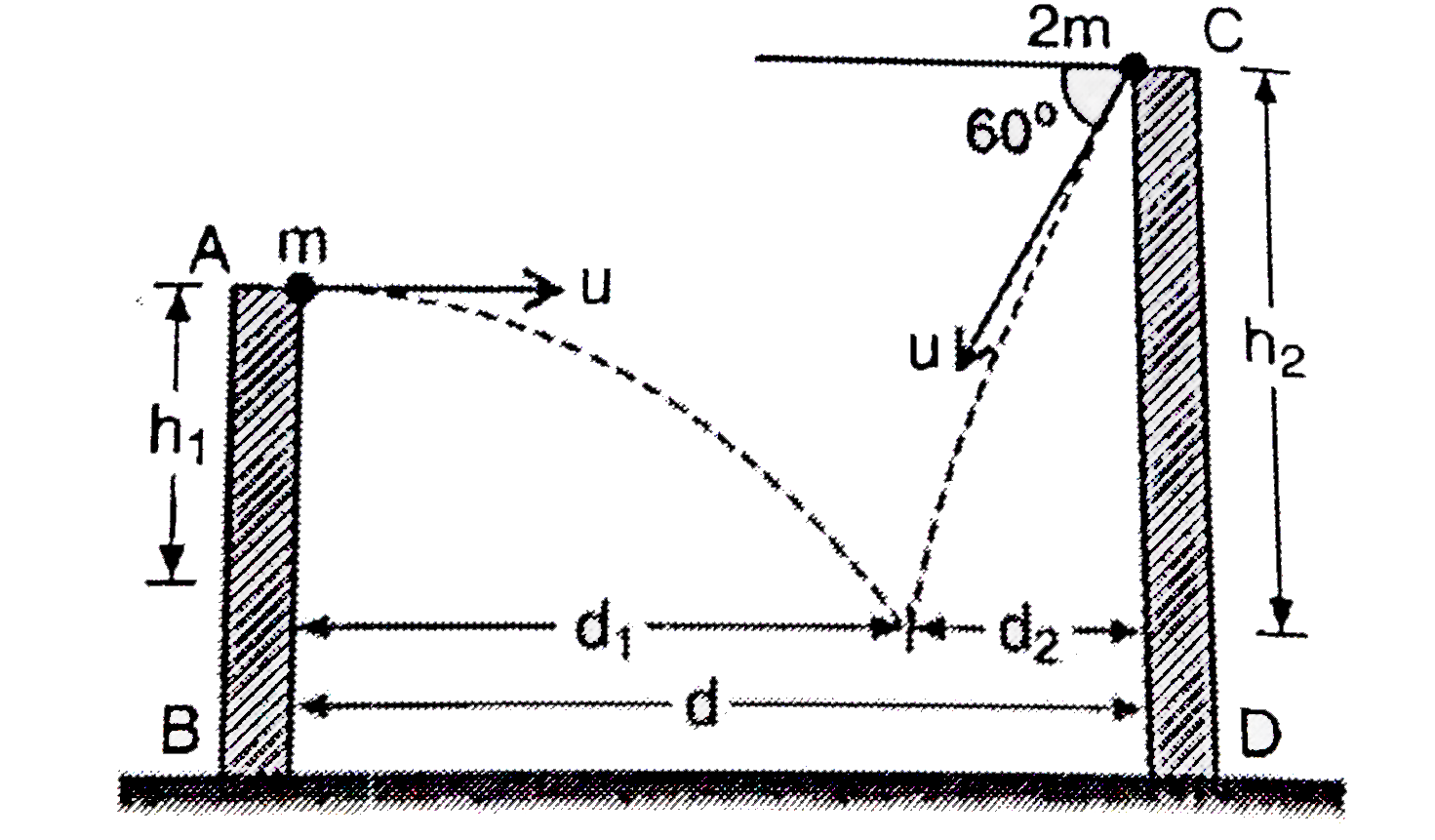
CD is 30m highfrom the ground . An object of mass m is thrown from the top of AB horizontally with a velocity 10m/s towards CD. simu ltaneously another object of mass 2 m is thrown from the top of CD at an angle of `60^(@)` to the horizotnal towards AB with the same magnitude of initial velocity as that of the first object. the two objects move in the same vertical plane, clollide in mid air and stick to each other, (a) Calcu late the distance d between the towers and (b) fin the position where the objects hit the ground.03:30View SolutionAn object of mass 5 kg is projecte with a velocity of `20ms^(-1)` at an angle of `60^(@)` to the horizontal. At the highest point of its path , the projectile explodes and breaks up into two fragments of masses 1kg and 4 kg. The fragments separate horizontally after the explosion, which releases internal energy such that `K.E.` of the system at the highest point is doubled. Calculate the separation betweent the two fragments when they reach the ground.
16:59View SolutionAn object `A` is kept fixed at the point ` x= 3 m` and `y = 1.25 m` on a plank `p` raised above the ground . At time ` t = 0 ` the plank starts moving along the `+x` direction with an acceleration ` 1.5 m//s^(2) `. At the same instant a stone is projected from the origin with a velocity `vec(u)` as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle ` 45(@)` to the horizontal . All the motions are in the ` X -Y `plane . Find ` vec(u)` and the time after which the stone hits the object . Take ` g = 10 m//s`
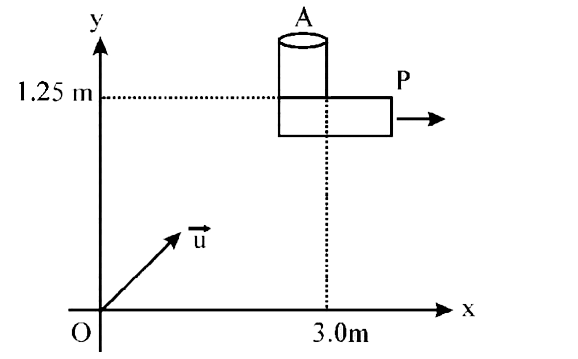 09:21View Solution
09:21View SolutionA body falling freely from a given height `H` hits an inlclined plane in its path at a height `h`. As a result of this impact the direction of the velocity of the body becomes horizontal. For what value of `h//H`, the body will take the maximum time to reach the ground.
05:42View SolutionA rocket moves horizontally with a constant velocity u at a height 1. A gu lded missile is fired vertically with a speed v when the rocket passes above it. Assuming that the missile always aims at the rocket with the constant speed v, find the time after which the missile strikes the rocket.
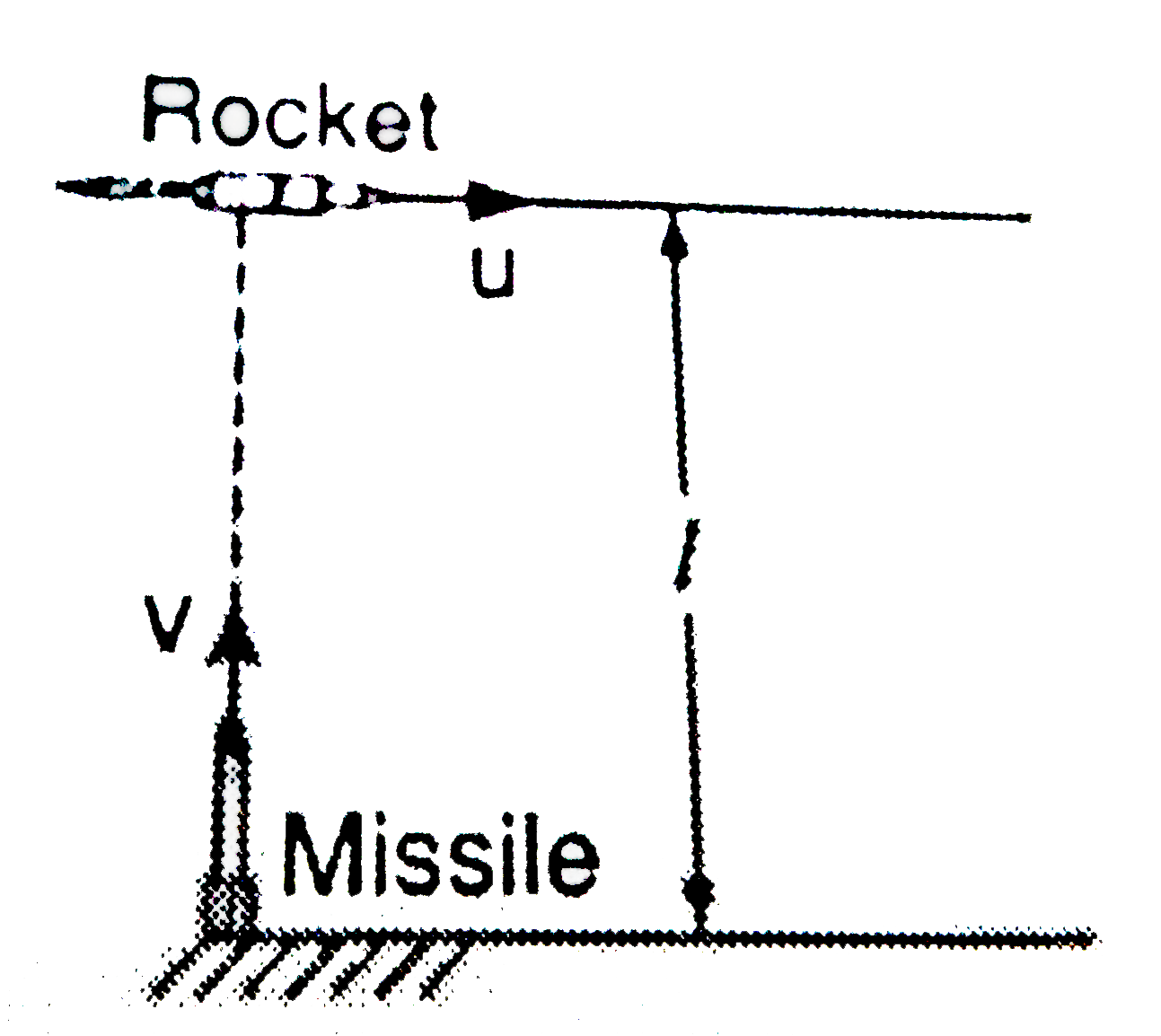 02:33View Solution
02:33View SolutionA man swims with avelocity `v_(mw)` in still water. When the water moves with a velocity `u_(w)(ltv_("new")^(2))` the man crosses the river to and fro in minimum time `T_(1)`. If the man intends to cross the river perpendicu larly, he takes time `T_(2)` for to and fro journey. Now he swims in the donwstream and comes back to his initial position by swimming upstream along the shore. For to and fro journey along the shore, the man takes a time `T_(3)`. find the relation between `T_(1),T_(2)` and `T_(3)` assuming equal distance overed by the man in each case.
02:41View SolutionIf the radius of earth is 6400km, calcu late (a) angu lar velocity (b) linear velocity and (c) radial accelration for a point on its equator considering its spin motion alone. What will be the values of above quantities if the pint is at the pole?
02:07View SolutionAn astronaout is rotating in a rotor of radius 4m. If he can withstand upto acc. Of 10g, then what is the maximum number of permissible revolutions? `(g=10m//s^(2))`
02:04View SolutionTwo satellites `S_(1)` and `S_(2)` revolve around a planet in coplanar circular orbits in the same sense their periods of revolution are 1 hour and 8hours respectively the radius of the orbit of `S_(1)` is `10^(4)` km when `S_(1)` is closest to `S_(2)` the angular speed of `S_(2)` as observed by an astronaut in `S_(1)` is :
03:39View SolutionA threaded rod with `12 turns//cm` and diameter `1.18 cm` is mounted horizontally. A bar with a threaded hole to match the rod is screwed onto the rod. The bar spins at `216 rev//min`. How long will it take for the bar to move `1.50 cm` along the rod ?
06:16View SolutionA wheel having radius `10cm` is coupled by a belt to another wheel of radius `30cm`. 1st wheel increases its angular speed from rest at a uniform rate of `1.57 rad//s^2`. The time for 2nd wheel to reach a rotational speed of `100 rev//min` is …(assume that the belt does not slip)
03:47View SolutionA spot light `S` rotates in a horizontal plane with a constant angular velocity of `0.1 rad//s`. The spot of light `P` move along the wall at a disatnce `3 m`. What is the velocity of the spot `P` when `theta = 45^(@)` ?
03:40View SolutionA particle is projected with a velocity `vecv=ahati+bhatj`. Find the radius of curvature of the trajectory of the particle at the (f) point of projection (ii) highest point.
02:12View SolutionA balloon starts rising from the earth's surface. The ascension rate is constant and equal to `v_(0)`. Due to the wind. The balloon gathers the horizontal velocity component `v_(x)=ky`, where k is a constnat and y is the height of ascent. Find how the following quantities depednd on the height of ascent.
(a) the horizontal drift of the balloon x (y)
(b) the total tangential and normal accelrations of the balloon.02:36View SolutionTwo particles of masses `m_(1)` and `m_(2)` are initially at rest infinite distance apart. If they approach each other under inverse square law of force `(F=k//r^(2))` find their speed of approach at the instant when they are distance d apart.
02:35View SolutionA particle of mass `10^-2kg` is moving along the positive x axis under the influence of a force `F(x)=-K//(2x^2)` where `K=10^-2Nm^2`. At time `t=0` it is at `x=1.0m` and its velocity is `v=0`.
(a) Find its velocity when it reaches `x=0.50m`.
(b) Find the time at which it reaches `x=0.25m`.19:08View SolutionA body projected vertically upwords from the top of a tower reaches the ground in `t_(1)` second . If it projected vertically downwards from the some top with same velocity ,it reaches the ground in `t_(2)`seconds . If it is just dropped from the top it reaches the ground in t second .prove that `t=sqrt(t_(1)t_(2))`
03:29View Solution(a) सिद्ध कीजिए कि किसी प्रक्षेप्य के x - अक्ष तथा उसके वेग के बिच के कोण को समय के फलन के रूप में निम्न प्रकार से व्यक्त कर सकते हैं
` theta (t) = tan ^(-1) ((v_(0y) - gt)/(v_(ox)))`
(d) सिद्ध कीजिए कि मूल बिंदु से फेंके गए कोण का मान ` theta_0 = tan ^(-1) ((4h_(m))/(R)) ` होगा | यहाँ प्रयुक्त प्रतीकों के अर्थ समान्य हैं |04:37View SolutionWhat is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution? Take the radius of the wheel as `R` and the `x`-axis as the forward direction?
04:13View SolutionThe horizontal and vertical distances covered by a projectile at tiem t are given by x=at and y=`bt^(2)+ct`, wehre a,b and c are constants. What is the magnitude of the velocity of the projectile 1 second after it is fired?
03:53View SolutionTaking the rotation and revolution of the earth into account, does a tree move faster during day or during night?
 04:21View Solution
04:21View SolutionIf a ball A is dropped while B is projected vertically down. Which ball will reach the ground (a) first (b) with greater velocity?
07:56View SolutionA man can throw a stone R m away:
(a) What is the maximum height to which the stone will rise?
(b) How high can the person throw the stone?05:04View SolutionTwo bodies P and Q are projected with velocites `sqrt(2)` u and u respectively. They cover the same horizontal distance. If body P is projected at `15^(@)` will the horizontal, then calcu late the angle of projection of body Q.
03:42View SolutionProve that:
The path of a projectile is a straight line.01:11View SolutionProve that for a projectile fired from level ground at an angle `theta` above the horizontal, the ratio of the maximum height H to the range R is given by
`(H)/(R)=(1)/(4)tan theta`03:03View SolutionWhen a particle is projected at an angle to the horizontal, it has range R and time of flight `t_(1)`. If the same projectile is projected with same speed at another angle to have the saem range, time of flight is `t_(2)`. Show that:
`t_(1)t_(2)=(2R//g)`04:34View SolutionIn an experiment for measuring 'g', a body is thrown vertically up in an evacuated tube and allowed to come back. If `DeltaT_(L)` is the time interval between the two passages of the object across a lower level and `DeltaT_(H)` the time interval between two passages across an upper level and H the distance between two levels as shown in Fig. 5.70 show that:
`g=(8H)/(DeltaT_(L)^(2)-DeltaT_(H)^(2))`
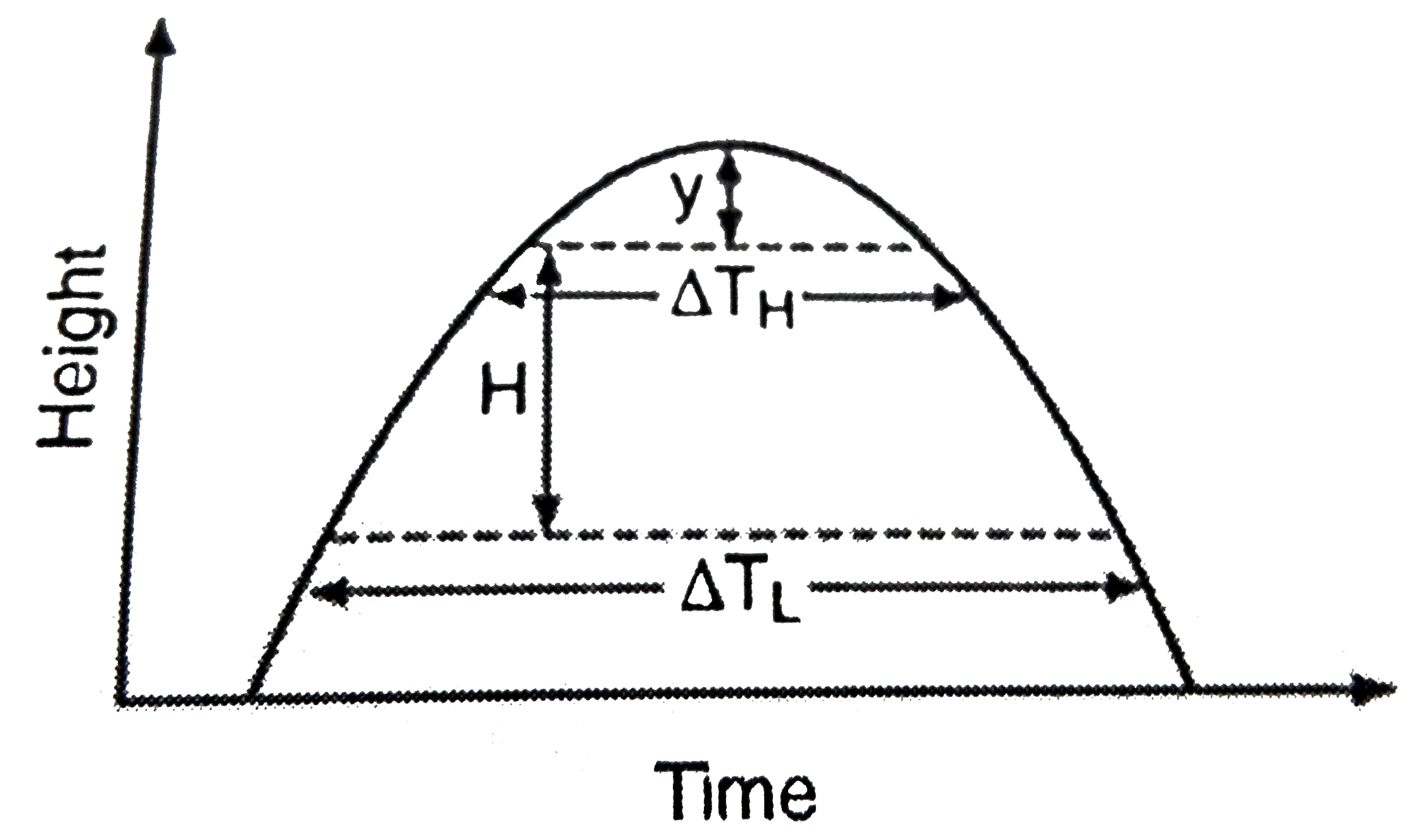 01:33View Solution
01:33View SolutionA bomb is dropped on a nenmy post by an aeroplane flying. With a horizontal velocity of 60km/hr and at a height of 490 m. how far the aeroplane must be from the enemy post at the time of dropping the bomb, so that it may directly hit the target? `(g=9.8m//s^(2))`
05:33View SolutionA fireman 50m away fro a burning building directs a stream of water from a firehouse at an angle `30^(@)` above the horizontal. If the velocity of the stream is 40m/s. at what height will the strea of water strike the building ? `(g=9.8m//s^(2))`
03:07View SolutionAn astronaut on a strange planet finds that he can jump a maximum horizontal distance of 30m if the initial speed is 9 m/s/ (a) what is the accelration of gravity on the planet? (b) what is the maximum height to which he can jump if he starts with thesame initial speed?
03:54View SolutionA particle of mass 3 kg takes 2 second to move from point A to B under the action of gravity and another constant force `vec(F)=(12hati-3hatj+12 hatk) N`, where the unit vector `hatk` is in the direction of upward vertical. The position vector of point B is `vec(r)_(B)=(15 hati-7hatj-6hatk)m` and velocity of the particle when it reaches B is `vec(V)_(B)=(12hati+hatj-4hatk m//s`.
(a) Find the velocity, `vec(V)_(A)`of the particle when it was at A.
(b) Find position vector, `vec(r)_(A)` of point A
(c) Find work done by the force `vec(F)` as the particle moves from A to B
(d) Find change in gravitational potential energy of the particle is it moves from A to B06:31View SolutionAn airplane is observed by two persons travelling at 60 km/hour in two vehicles moving in opposite directions on a straight road. To an observer in one vehicle the plane appears to cross the road track at right angles while to the observer in the other vehicle the angle appears to be `45^(@)` . At what angle does the plane actually cross the road track and what is its speed relative to ground?
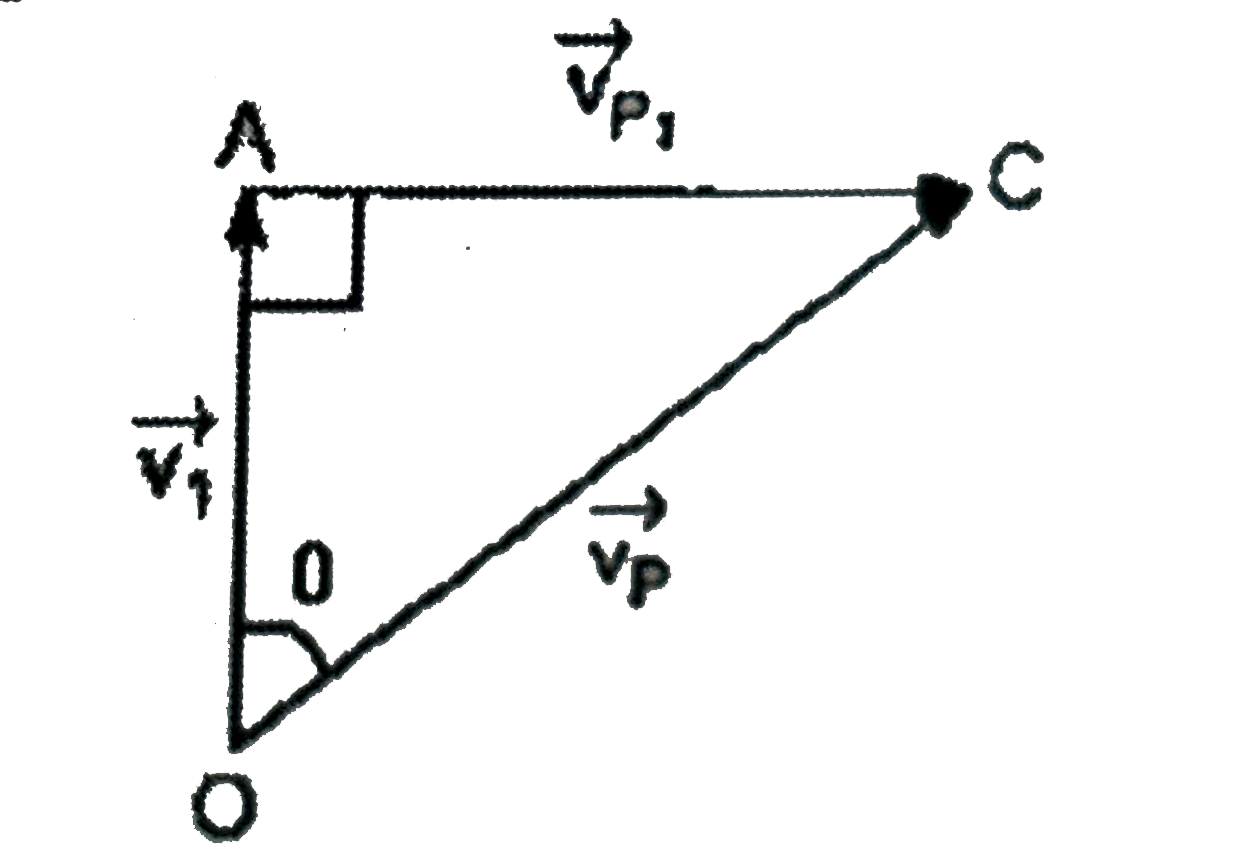 07:30View Solution
07:30View SolutionA motor boat set out at 11a.m. from a position `-6hati-2hatj` relative to a marker buoy and travel at a steady spee dof magnutdue `sqrt(53)` on a direc course to intercept a ship. The ship maintains a steady velocity vector `3hati+4hatj` and at 12 noon is at a postion `3hati-hatj` form the body. Find (a) the velocity vector of the motor boat, (b) the time of interecption and (c) the position vector of point of interception from the buoy if distances are measured in mkilometeres and speds i kilometre per hour.
02:28View SolutionA man can row a boat at 4.0km/hr in still water. A river flows at 2.0km/hr. (a) if he is crossing the river, in what direction the oat shou ld go to reach a point directly opposite to his staring point? (b) if the river is 4.0km wide how long will it take him to cross the river? (c) How long will it take him to row 2.0km down the river and then back to his starting point? (d) How long will it take him to row 2.0 km up the river and then back to his starting point? (e) in what direction the boat shou ld go, if he wants to cross he river in teh smallest possible time?
02:07View SolutionA projectile is lauched with a velocity u at right angles to the along, which in inclined at an angle 1 with the horizontal. Derive an expression for the distance R to the point of impact.
 01:09View Solution
01:09View SolutionA shell is fired vertically from a cannon which is travelling at constant speed u=30km/hr. the projectile leaves the connon with a velocity `v_(r)=20` m/s relative to the cannon . Show that the shell will land on the vehicle at the gun location and calcu late the distance by the vehicle during the flight of shell.
 01:05View Solution
01:05View SolutionA stone at the end of a string is whirled in a vertical circle of radius r=1.20 m at a constant speed u=1.50m/s. the centre of the string is 1.50m above the ground. What is the range of the stone if it is released when the string is inclined at `30^(@)` with the horizotnal (a) at A(b) at B? What is the accelration of the stone: (c) just before rleaseat A (d) just after release at A?
 02:34View Solution
02:34View SolutionTwo particles are projected simu ltaneously from points A and B respectively and they move in same plane. Find.
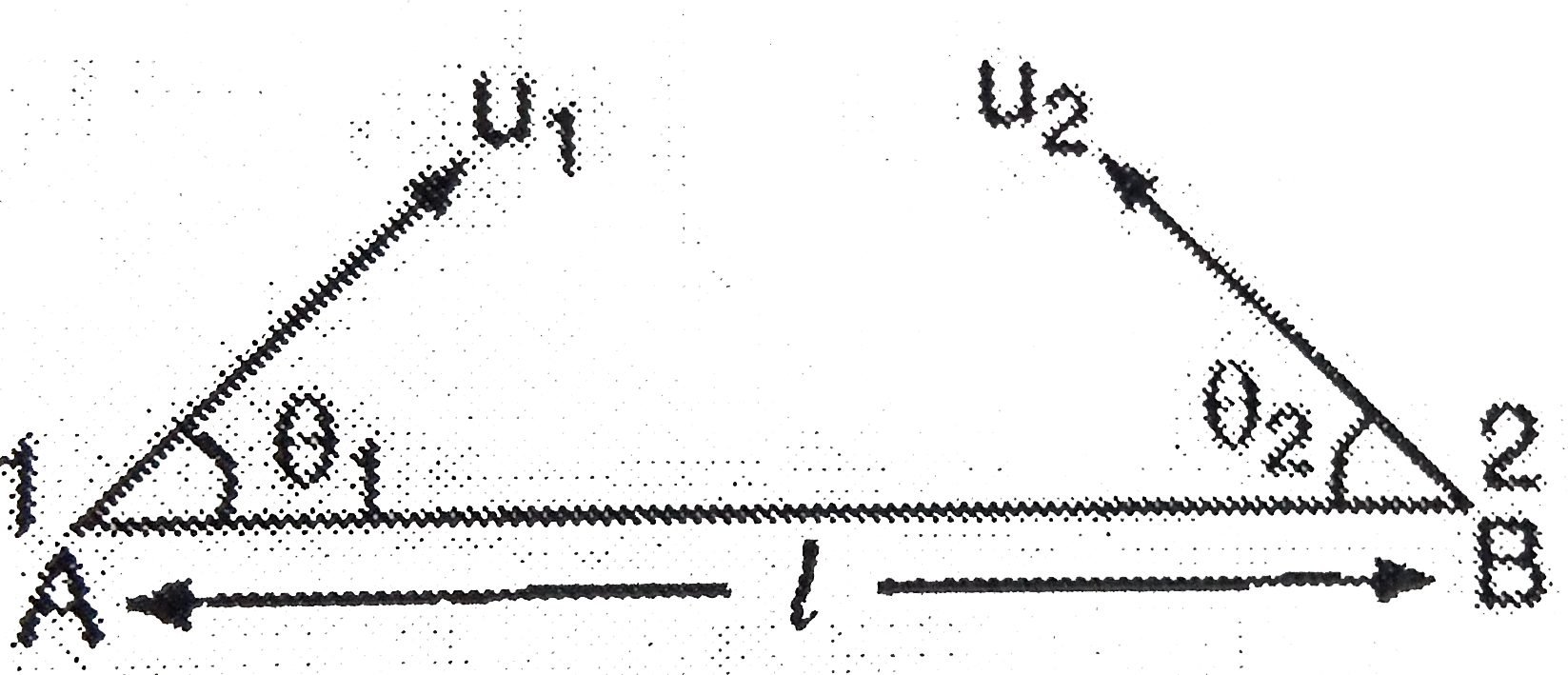
(a) the separation when they are closest to each other.
(b) the time elapsed to come closest to each other.
(c) condition that they collide in air.
(d) initial velocity of approch between the particles.
(e) initial angu lar velocity of first particle w.r.t. second particle.03:41View SolutionA particle moves in x-y plane according to ru le x`=a sin omegat` and y=`a cos omegat`. The particles follows:
03:14View SolutionThe x and y co-ordinates of a partilce at any time t are given by:
`x=7t+4t^(2)` and `y=5t`
The acceleration of the particle at 5s is:00:57View SolutionThe height `y` and distance `x` along the horizontal plane of a projectile on a certain planet are given by `x = 6t m` and `y = (8t^(2) - 5t^(2))m`. The velocity with which the projectile is projected is
02:27View SolutionAn object is projected so that it just clears two walls of height 7.5 m and with separation 50m from each other. If the time of passing between the walls is 2.5s, the range of the projectile will be (g=`10m//s^(2)`)
09:53View SolutionA body mass `2kg` has an initial velocity of 3 metre//sec along OE and it is subject to a force of `4N` in a direction perpendicular to OE. The distance of body from `O` after 4 sec will be:
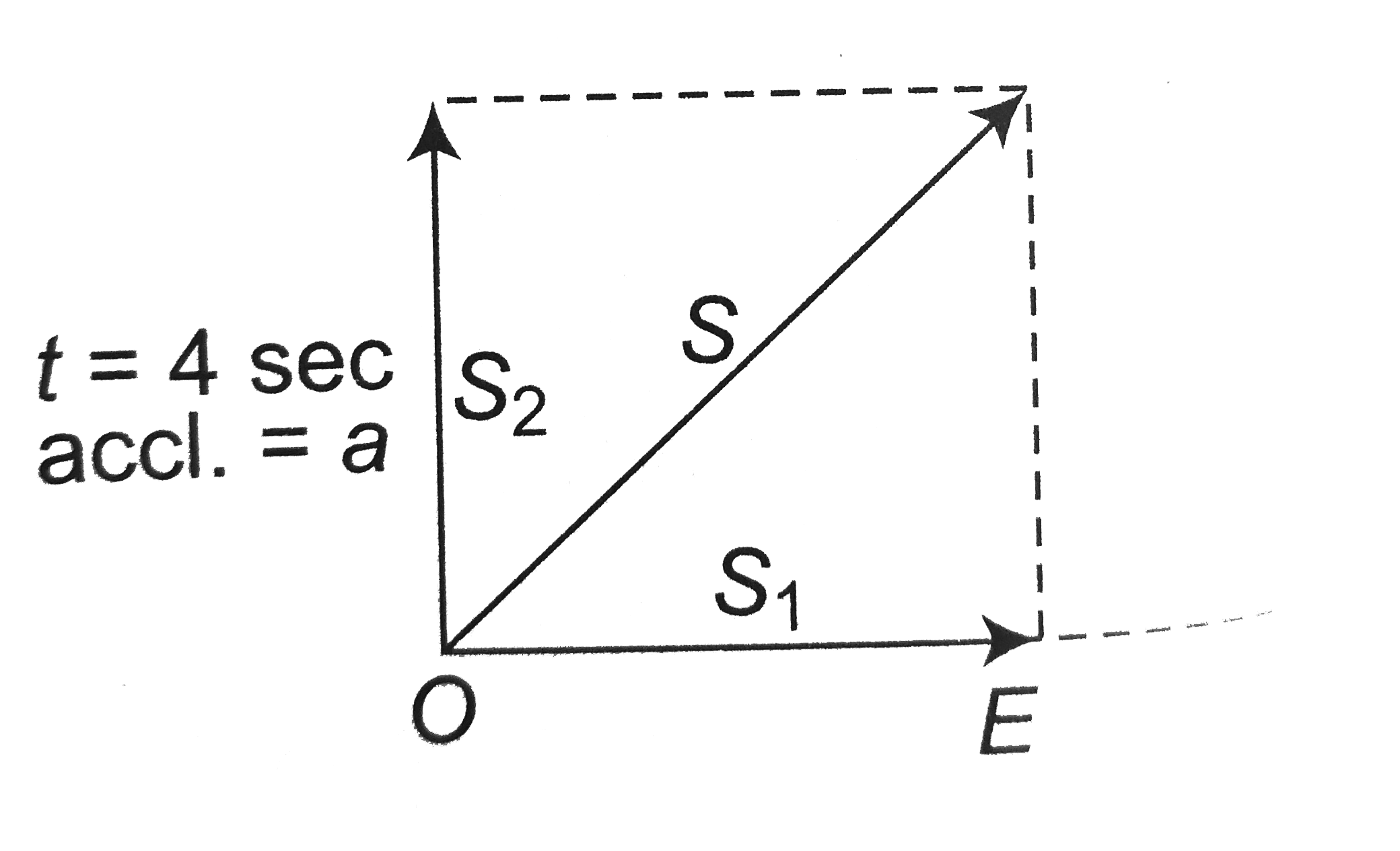 03:45View Solution
03:45View SolutionIf a force is applied at an angle to a body moving along a straight line:
00:59View SolutionA particle moves along the positive branch of the curve `y = (x^(2))/(2)` where `x = (t^(2))/(2),x` and y are measured in metres and t in second. At `t = 2s`, the velocity of the particle is
01:31View SolutionA bu llet is fired with a gun from a tower horizontally with a velocity 400m//s. at the same time a stone is droppe dform the same tower:
03:57View SolutionTwo bu llets are fired simu ltaneously, from the same level and in the horizontal direction, over a lake. The speed of one is 196m/s and of the other is 98m/s and of the other 98 m/s. Assuming that the air resistance is negligible and the lake is still the bu llet which is moving faster will, compared to the slower one, fal in the water:
03:57View SolutionA particle moves along the parabolic path `y=ax^(2)` in such a The accleration of the particle is:
03:19View SolutionA ball is thrown upwards and returns to the ground describing a parabolic path. Which of the following quantities remains constant ?
03:14View SolutionIf a body A of mass M is thrown with velocity V at an angle of `30^(@)` to the horizontal and another body B of the same mass is thrown with the same speed at an angle of `60^(@)` to the horizontal. The ratio of horizontal range of A to B will be
01:26View SolutionIt was calculated that a shell when fired from a gun with a certain velocity and at an angle of elevation `5pi//36` radius should strike a given target. In actual practice it was found that a hill just intervened in the trajectory. At what angle of elevation should the gun be fired to hit the target ?
03:38View SolutionA ball of mass `m` is thrown vertically upwards. Another ball of same mass is thrown at an angle `theta` to the horizontal. If the time if flights for both is same, the ratio of maximum height attained by them
03:17View SolutionA particle is projected at an angle of `45^(@)` with a velocity of `9.8 ms^(-1)`. The horizontal range will be (Take, `g = 9.8 ms^(-2))`
01:48View SolutionThe range of a projectile launched at an angle of `15^(@)` with horizontal is 1.5km. The range of projectile when launched at an angle of `45^(@)` to the horizontal is
02:30View SolutionAn object is thrown along a direction inclined at an angle of `45^(@)` with the horizontal direction. The horizontal range of the particle is equal to
03:49View SolutionAt what angle to the horizontal should an object be projected so that the maximum height reached is equal to the horizontal range.
02:04View Solutiona projectile is fired from the surface of the earth with a velocity of `5ms^(-1)` and angle `theta` with the horizontal. Another projectile fired from another planet with a velocity of `3ms^(-1)` at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth.The value of the acceleration due to gravity on the planet is in `ms^(-2)` is given `(g=9.8 ms^(-2))`
03:22View SolutionA stone is thrown with a velocity V making an angle `theta` with the horizontal. The horizontal distance covered by it, before it falls to the ground, is maximum when `theta` is equal to:
02:29View SolutionA body is projected with a speed (u) at an angle to the horizontal to have maximum range. What is its velocity at the highest point ?
03:30View SolutionA grasshopper finds that he can jump a maximum horizontal distance of 0.8m. With what speed can be travel along the road if he spends a negligible time on the ground?
04:12View SolutionA cricket ball is hit for a six the bat at an angle of `45^(@)` to the horizontal with kinetic energy K. At the highest point, the kinetic energy of the ball is
01:42View SolutionThe gretest height to which a man can throw a stone is h. the greatest distance to which he can throw will be:
02:51View SolutionA bomber if flying horizontally with a constant speed of 150 m/s at a height of 78.4m. The pilot has to drop a bomb at the enemy target. AT what horizontal distance from the target shou ld be release the bomb?
03:39View SolutionA box containing food supplies is released from an aeroplane moving horizontally at a height of 490 m with a velocity of 180 km/hr. the box will move horizontally while falling nust before striking against the earth by:
05:19View SolutionA particle is thrown with speed `u` at an angle `alpha` with horizontal from the ground. After how much time, the velocity of particle will make an angle `beta` with horizontal.
08:58View SolutionA body is dropped from a plane moving with constant horizontal velociy. The path of the body as seen by a person on the plane will be
03:35View SolutionA projectile is fired horizontally with an initial speed of 20 m/s/ its horzontal speed 3 sec later is:
02:31View SolutionA particle is projected upwards with a velocity of `100 m//s` at an angle of `60^(@)` with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking `g = 10 m//s^(2)`.
06:18View SolutionA cannon ball has the same range R on a horizontal plane for two angles of projection. If `h_(1)` and `h_(2)` are the greatest heights in the two paths for which this is possible then:
02:52View SolutionA ball rolls off top of a staircase with a horizontal velocity `u m s^-1`. If the steps are `h` metre high and `b` mere wide, the ball will just hit the edge of `n th` step. Find the value of `n`.
02:16View SolutionA particle moves along the positive branch of the curve `y = (x^(2))/(2)` where `x = (t^(2))/(2),x` and y are measured in metres and t in second. At `t = 2s`, the velocity of the particle is
01:31View SolutionWater is flowing through a horizontal pipe fixed at a height of 2 m above the ground as shown in Fig. 5.90. water strikes ground at a distance of 3m from the pipe. The speed of water as it leaves the pipe is:
 00:50View Solution
00:50View SolutionThe current velocity of river grows in proportion to the distance from its bank and reaches the maximum value `v_0` in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
07:54View SolutionA particle is project d from point A with velocity u at an angle `alpha` with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
04:24View SolutionA projectille can have the same range` R` for two angles of projection. If ` t_(1)` and `t_(2)` be the time of flight in the two cases, then find the relation between ` t_(1), t_(2)` and `R` .
02:48View SolutionIn `1.0 s`, a particle goes from point `A` to point `B` , moving in a semicircle of radius `1.0 m ` (see figure ). The magnitude of the average velocity
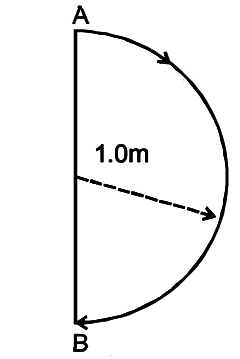 01:26View Solution
01:26View SolutionA particle is thrown above, then correct `v-t` graph will be
02:37View Solution
All Questions questions and complete solutions for chapter MOTION IN TWO AND THREE DIMENSIONS of GR BATHLA & SONS PHYSICS (HINGLISH) of Class 11
