Complete Solutions to Exercises of chapter REST AND MOTION : KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | REST AND MOTION : KINEMATICS |
| HC VERMA | Exercises |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
A man has to go 50 m due north, 40 m due east and 20 m due south to reach a field, What distance he has to walk to reach the field? b.What is his displacement from his house to the field?
View SolutionA particle starts from the origin, goes along the X-axis to the point (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionIt is 260 km from Patna to Ranchi by air and 320 km by road.an aeroplane takes 30 minutes to go from Patna to Ranchi whereas a delux bus takes 8 hours. a.Find the verge speed of the plane. b.Find the verage speed of the bus. C. Find the average velocity of the plane. d. Find the average velocity of the bus.
View SolutionWhen a person leaves his home for sightseeing by his car, the meter reads 12352 km. When he returns home after two hours the reading is 12416 km. A. What is the average speed of the car during this period? B. What is the average velocity?
View SolutionAn athelete takes 2.0 s to reach his maximum speed of 18.0 km/h. What is the magnitude of his average acceleration?
View SolutionThe speed of a car as a function of time is shown in figure.
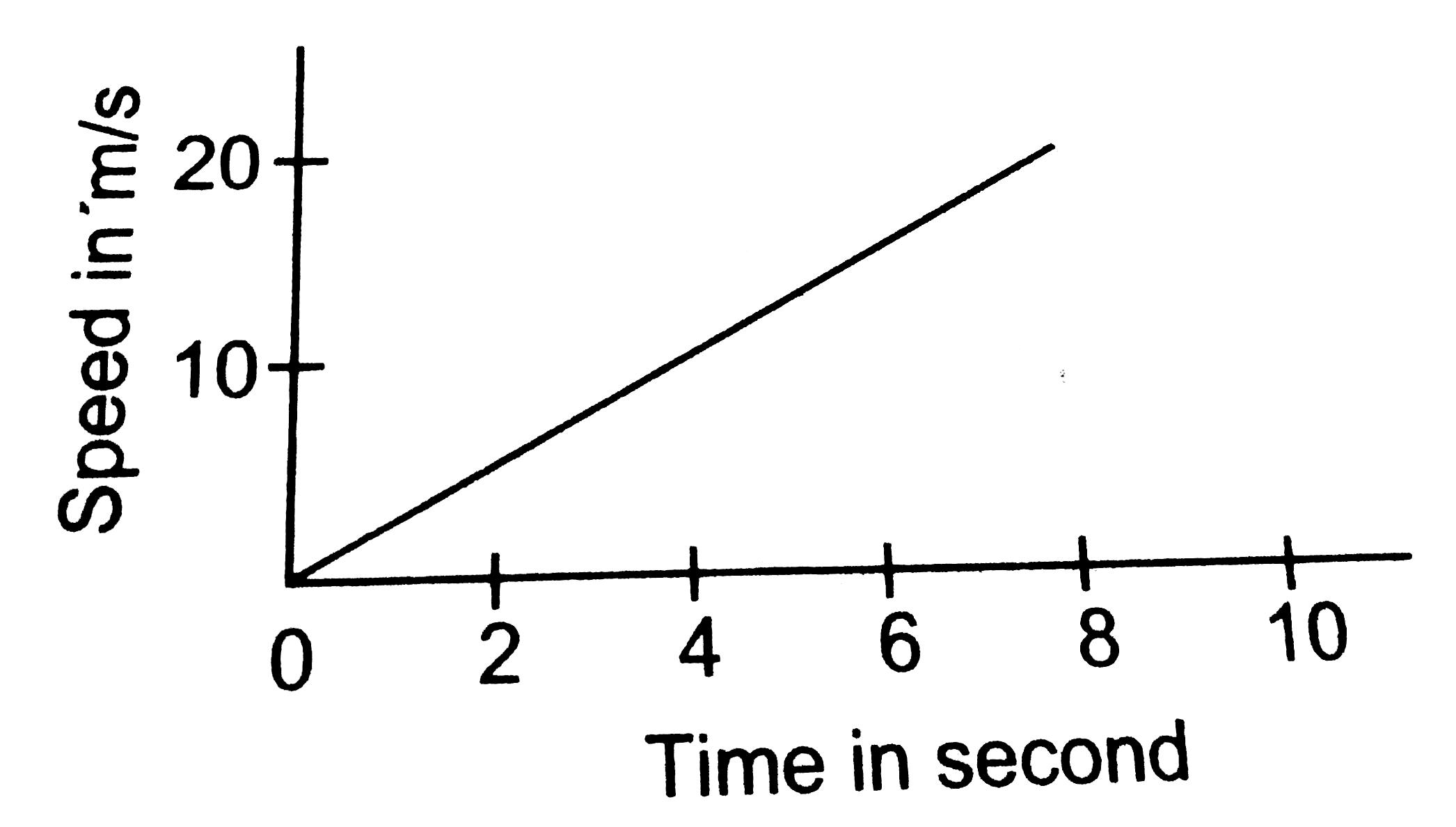
Find the distance travelled by the car in 8 seconds and its acceleration.
View SolutionThe acceleration of a cart started at t=0 varies with time as shown in figure. Find the distance travelled in 30 seconds and draw the position time graph.

View Solutionfigure
 shows the graph of velocity versus tie for a particle going along the X-axis. Find a. the acceleration, b. The distance travelled in 0 to 10 s and c. the displacement in 0 to 10 s.
shows the graph of velocity versus tie for a particle going along the X-axis. Find a. the acceleration, b. The distance travelled in 0 to 10 s and c. the displacement in 0 to 10 s.
View SolutionFigure shows the graph of the x-coordinaste of a particle going along the X-axis as a function of time.Find a. te average velocity during 0 to 10s, b. instantaneous velocity at 2,5,8 and 12s.

View SolutionFrom the velocity time plot shown in figure find the distance travelled by the particle dureing the first 40 seconds. Also find the average velocity during this period.

View SolutionFigure shows x-t graph of a particle. Find the Time T such that the average velocity of the particle during the period 0 to T is Zero.
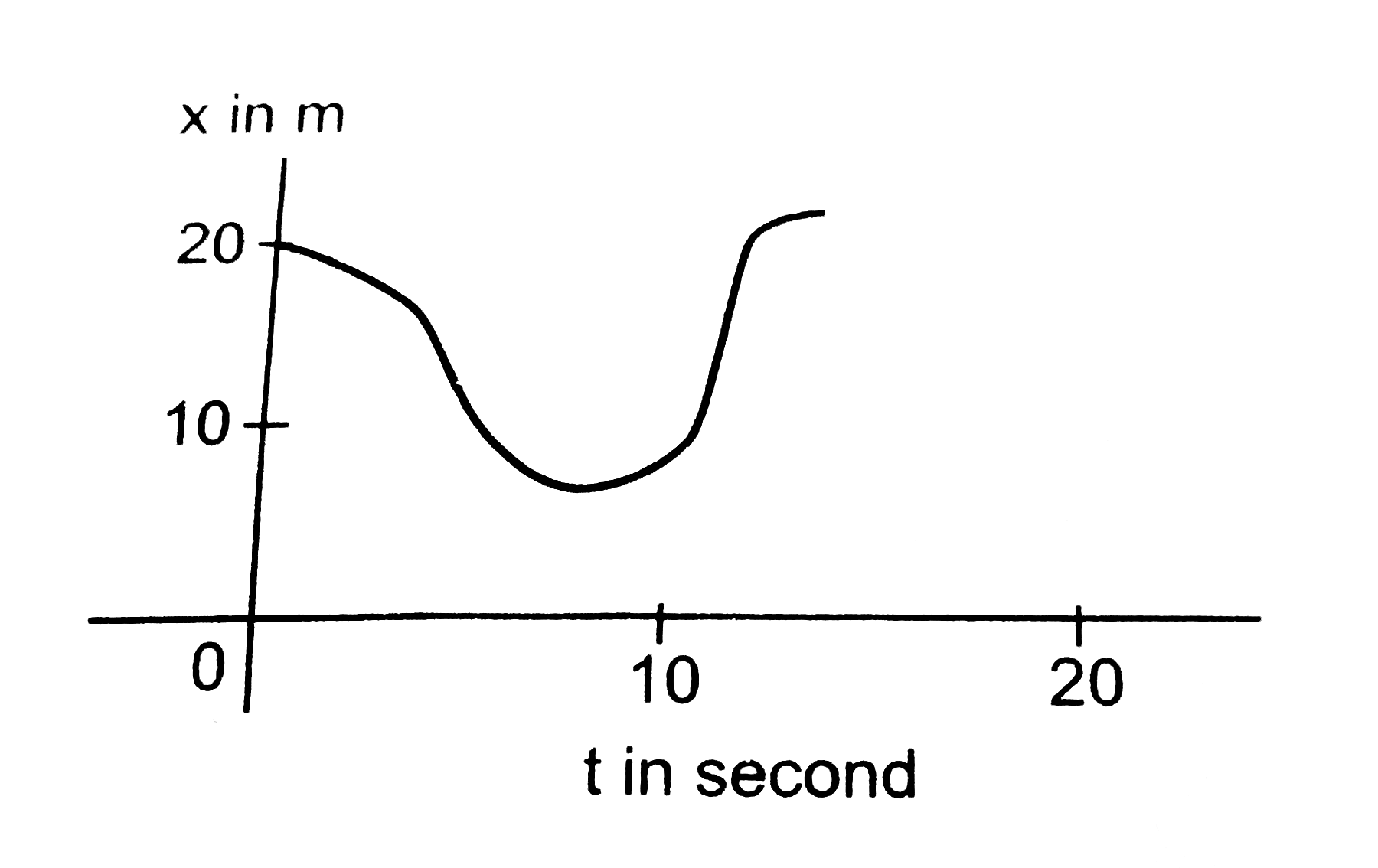
View SolutionA particle starts from a point A and travels along the solid curve shown in figure. Find approximately the position B of the particle such that the average velocity between the positions A and B has the same direction as the instantaneous velocity at B.

View SolutionAn object having a velocity 4.0 m/s is accelerated at the rate of `1.2 m/s^2` for 5.0s. Find the distance travelled during the period of acceleration.
View SolutionA person travelling at 43.2 km/h applies the brake giving a deceleration of `6.0 m/ss^2` to his scooter. How far will it travel before stopping?
View SolutionA train starts from rest and moves with a constant accelerationof 2.0`m/s^2` for half a minute. The brakes are then applied and the train comes to rest in one minute. Find a. the total distance moved by the train, b. the maximum speed attained by the train and c. the position(s) of the train at half the maximum speed.
View SolutionA bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
View SolutionA bullet going with speed 350 m/s enters concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
View SolutionA particle starting from rest moves with constant acceleration. If it takes 5.0 s to reash the speed 18.0 km/h find a. the average velocity during this period, and b. the distance travelled by the particle during this period.
View SolutionA driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he ils driving a car at a speed of 54 km/h and the brakes cause a deceleration of `6.0 m/s^2`, find the distance travelled by the car after he sees the need to put the brakes on.
View SolutionA police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h.
The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
View SolutionA car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
View SolutionA ball is projected vertically upward with speed of 50 m/s. Find a. the maximum height, b. the time to reach the maximum height, c. the speed at half the maximum height. Take g=`10 m/s^2`.
View SolutionA ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
View SolutionA stone is thrown vertically upward with a speed of 28 m/s. (a) Find the maximum height reached by the stone. (b)Find its velocity one second before it reaches the maximum height. (c)Does the answer of part b change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s?
View SolutionA person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
View SolutionA healthy young man standing at a distance of 7 m from 11.8 m high building sees a kid slipping from the top floor. With what speed (assumed uniform) should he run to catch the kid at the arms height (1.8m)?
View SolutionAn NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (ie the distance from the tree at the instant) will receive the berry on his uniform?
View SolutionA ball is dropped from a height. If it takes 0.200 s to cross thelast 6.00 m before hitting the ground, find the height from which it was dropped. `Take g=10 m/s^2`.
View SolutionA ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball in and assuming it to be uniform.
View SolutionAn elevator is descending with uniform acceleration.To measure the acceleration, a person in the elevator drops a coin at momen the elevator strts. The coin is 6 ft asbove the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate these dta the acceleration of the elevator.
View SolutionA ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find a. the time it takes to reach the ground, b. the horizontal distance it travels before reaching the ground c. the velocity (direction and magnitude) with which it strikes the ground.
View SolutionA ball is thrown at a speed of 40 m/s at an angle of `60^0` with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take `g=10 m/s^2`.
View SolutionIn a soccer practice sesson of the football is kept at the centre of the field 40 yards from the 10 ft hight goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at angle of `45^0` to the horizontal. Will the ball reach the goal post?
View SolutionA popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situatted at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middlefilngers and making the throw. If he projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed shold it be projected so that it directly hits the stationary goli without falling on the ground earlier?
View SolutionFigure shows a 11.7 ft wide ditch with the approach roads at and angle of `15^0` with the horizontal. With what minimum speed should a mororbike be moving on the road so that it safely croses the ditch?

Assume that the length of thebike is 5 ft, and it leaves the road when the front part runs out of the approch road.
View SolutionA person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed o 15.0 ft/s, how short will the packet fall?
View SolutionA ball is projected from a point on the floor wilth a speed of 15 m/s at an angle of `60^0` with the horizontal. Will ilt hit a vertical wall 5 m away from the point of projection and perpendiculaer to the plane of projection without and perpendicular to the plane of projection without hitting the floor? will the answer differ if the wall is 22 m away?
View SolutionFind the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with speed u at angle `theta` with the horizontal.
View SolutionA bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane.Is the statement true if the plane flies with uniform speed but not horizontally?
View SolutionA boy standing on a long railroad car throuws a ball straight upwards. The car is moving on the horizontal road with an acceleration of `1m/s^2` and the projectioon velocity inte vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
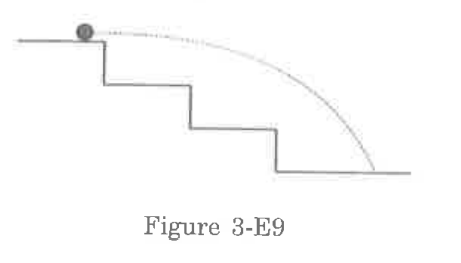
View SolutionA staircase contains three steps each 10 cm high and 20 cm wide figure. What should be the minimum horizontal velocity of a bal rolling off the upper most plane so as to hit directly the lowest plane?
View SolutionA person is standing on a truck moving with a constant velocity of 14.7 m/s o a hrozontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection. a. as seen from the truck b. as seen fromt the road.
View SolutionThe benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one meter above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of `53^0` with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
View SolutionA man is sitting on the shore of a river. He is in the line of a 1.0 m long boat and is 5.5 m away from the centre of the boat. He sishes to throw an apple into the boat. If he can throuw the apple only wihta speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level
View SolutionA `400 m` wide river is flowing at a rate of `2.0 m s^-1`. A boat is sailing with a velocity of `10 m s^-1` with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?
View SolutionA swimmer wishes to cross a `500 m` river flowing at `5 km h^-1`. His speed with respect to water is `3 km h^-1`. The shortest possible time to cross the river is.
View SolutionA swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If the reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
View SolutionAn aeroplane has to go from a point A to another point B, `500 km` away due `30^@` east of north. Wind is blowing due north at a speed of `20 m//s.` The air-speed of the plane is `150 m//s.` (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.
View SolutionTwo friends A and B are standing a distance x apartin an open field and wind is blowing from A to B.A beats a drum and B hears the sound `t_1` timed after he sees the event. A and B intechange their positions and te experiment is repeated. This time B hears teh drum `t_2` time after he sees the event. Calculte teh velocity of sound in still air v and the velocity of wind u. Neglect the tiem light takes in travelling between the friends.
View SolutionTwo friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beats a drum and B hears the sound `t_1` timed after he sees the event. A and B interchange their positions and the experiment is repeated. The velocity of sound in still air is `v` and the velocity of wind is `u`. This time B hears the drum `t_2` time after he sees the event. Suppose A and B change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation `x`. What will be the time lag B finds between seeing and hearing the drum beating by A?
View SolutionSix particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
View Solution
Exercises questions and complete solutions for chapter REST AND MOTION : KINEMATICS of HC VERMA PHYSICS (ENGLISH) of Class 11