Complete Solutions to All Questions of chapter SPECIFIC HEAT CAPACITIES OF GASES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SPECIFIC HEAT CAPACITIES OF GASES |
| HC VERMA | All Questions |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
`0.32 g` of oxygen is kept in a rigid container and is heated. Find the amount of heat needed to raise the temperature from `25^0 C to 35^0 C`. The molar heat capacity of oxygen at constant volume is `20 J K^(-1) mol^(-1)`.
View SolutionA tank of volume `0.2 m^3` contains helium gas at a temperature of `300 K` and pressure `1.0 xx 10^5 N m^(-2)`. Find the amount of heat required to raise the temperature to `400 K`. The molar heat capacity of helium at constant volume is `3.0 cal K^(-1 ) mol^(-1)`. Neglect any expansion in the volume of tank.
View SolutionThe molar heat capacity of a gas at constant volume is found to be `5 cal mol^(-1) K^(-1)`. Find the ratio`gamma = C_p/C_v` for the gas. The gas constant `R=2 cal mol^(-1) K^(-1).
View SolutionDry air at `15^0 C` and 10 atm is suddenly released at atmospheric pressure. Find the final temperature of the air `[C_p / C_v = 1.41]`.
View SolutionCalculate the internal energy of `1 g` of oxygen STP.
View SolutionCalculate the value of mechanical equivalent of heat from the following data. Specific heat capcity of air at constant volume =`170 cal kg^(-1) K^(-1) , gamma = C_p/ C_v = 1.4` and the density of air at STP is `1.29 kg m^(-3)`. Gas constant`R = 8.3 JK^(-1) mol^(-1)`.
View SolutionAn ideal gas has a molar heat capacity at constant pressure of `Cp = 2.5 R`. The gas is kept in a closed vessel of volume `0.0083 m^(3)`, at a temperature of `300 K` and a pressure of 1.6 x 10^(6) Nm^(-2). An amount 2.49 x 10^(4) J of heat energy is supplied to the gas. calculate the final temperature and pressure of the gas.
View SolutionA sample of ideal gas `(gamma = 1.4)` is heated at constant pressure. If `140 J` of heat is supplied to gas, find `DeltaU` and `DeltaW`.
View SolutionAn experiment is performed to measure the molar heat capacity of a gas at constant pressure using Regnault's method. The gas is initially contained in a cubical reservoir of size ` 40 cm xx 40 cm xx 40 cm xx at 600 kPa at 27^0C`. A part of the gas is brought out, heated to 100^0C and is passed through a calorimeter at constant pressure. The water equivalent of the calorimeter and its contents increases from `20^0C to 30^0C` during the experiment and the pressure in the reservoir decresases to `525 kPa`. Specific heat capacity of water =`4200 J kg^(-1) K^(1). Calculate the molar heat capacity Cp from these data.
View SolutionA quantity of air is kept in a container having walls which are slightly conducting. The initial temperature and volume are `27^0C` (equal to the temperature of the surrounding) and `800cm^(3)` respectively. Find the rise in the temperature if the gas is compressed to `200 cm^(3)` (a) in a short time (b) in a long time . Take gamma= 1.4.
View SolutionA sample of gas `(gamma = 1.5)` is taken through an adiabatic process in which the volume is compressed from `1600 cm^(3) to 400 cm^(3)`. If the initial pressure is `150 kPa`, (a) what is the final pressure and (b) how much work is done by the gas in the process?
View SolutionTwo moles of a gas `(gamma=5//3)` are initially at temperature `27^@C` and occupy a volume of 20 times. The gas is first expanded at constant pressure until the volume is doubled. Then, it is subjected to an adiabatic change until the temperature returns to its initial value.
(a) Sketch the process on a p-V diagram.
(b) What are the final volume and pressure of the gas?
(c) What is the work done by the gas?
View SolutionAn ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. the piston and the cylinder have equal cross sectional area A. when the piston is in equilibrium, the volume of the gas is `V_(0)` and its pressure is `P_(0)`. the piston is slightly displaced from the equilibrium posittion and released. assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionTwo vessels of volume `(V_1) and (V_2)` contain the same ideal gas. The pressures in the vessels are `(P_1) and (P_2) ` and the temperatures are `(T_1) and (T_2)` respectively . The two vessels are now connected to each other through a narrow tube. Assuming that no heat is exchanged between the surrounding and the vessels, find the common pressure and temperature attained after the connection.
View SolutionTwo moles on ideal gas with `gamma=5/3` is mixed with 3 moles of another ideal non reacting gas with `gamma=7/5` .The value of `(C_p)/(C_v)` for the gasous mixture is closer to :
View SolutionA diatomic gas `(gamma =1.4)` does 200 J of work when it is expanded isobarically. Find the heat given to the gas in the process.
View SolutionCalculate the ratio `(C_p / C_v)` of oxygen from the following data . Speed of sound in oxygen`(= 32g mol^(-1))` and the gas constant `(R = 8.3 J K ^(-1) mol^(-1))`.
View SolutionCan we define specific heat capacity at constant temperature?
View SolutionCan we define specific heat capacity at constant for an adiabatic process?
View SolutionDoes a solid also have two kinds of molar heat capacities `C_p` and `C_v`? If yes , do we have `C_p gt C_v`? Is `C_p - C_v = R`?
View SolutionIn a real gas the internal energy depends on temperature and also on volume. The energy increases when the gas expands isothermally. Looking into the derivation of `(C_p - C_v = R_1)` find whether `(C_p - C_v)` will be more than R, less than R, or equal to R for a real gas.
View SolutionCan a process on an ideal gas be both adiabatic and isothermal. ?
View SolutionShow that the slope of `p-V` diagram is greater for an adiabatic process as compared to an isothermal process.
View SolutionCan two states of an ideal gas be connected by an isothermal process as well as an adiabatic process?
View SolutionThe ratio `(C_p / C_v)` for a gas is 1.29 . What is the degree of freedom of the molecules of this gas?
View SolutionWork done by a sample of an ideal gas in a process A is double the work done in another process B. The temperature rises through the same amount in the two processes. If `(C_A and C_B) be the molar heat capacities for the two processes,
View SolutionFor a solid with a small expansion coefficient,
View SolutionThe value of `C_(p) - C_(v)` is `1.09R` for a gas sample in state `A` and is `1.00R` in state `B`. Let `T_(A),T_(B)` denote the temperature and `p_(A)` and `p_(B)` denote the pressure of the states `A` and `B` respectively. Then
View SolutionLet `(C_v) and (C_p)` denote the molar heat capacities of an ideal gas at constant volume and constant pressure respectively . Which of the following is a universal constant?
View Solution70 calories of heat is required to raise the temperature of 2 mole of an ideal gas at constant pressure from 30^@C to 35^@C . The amount of heat required to raise the temperature of the same gas through the same range at constant volume is
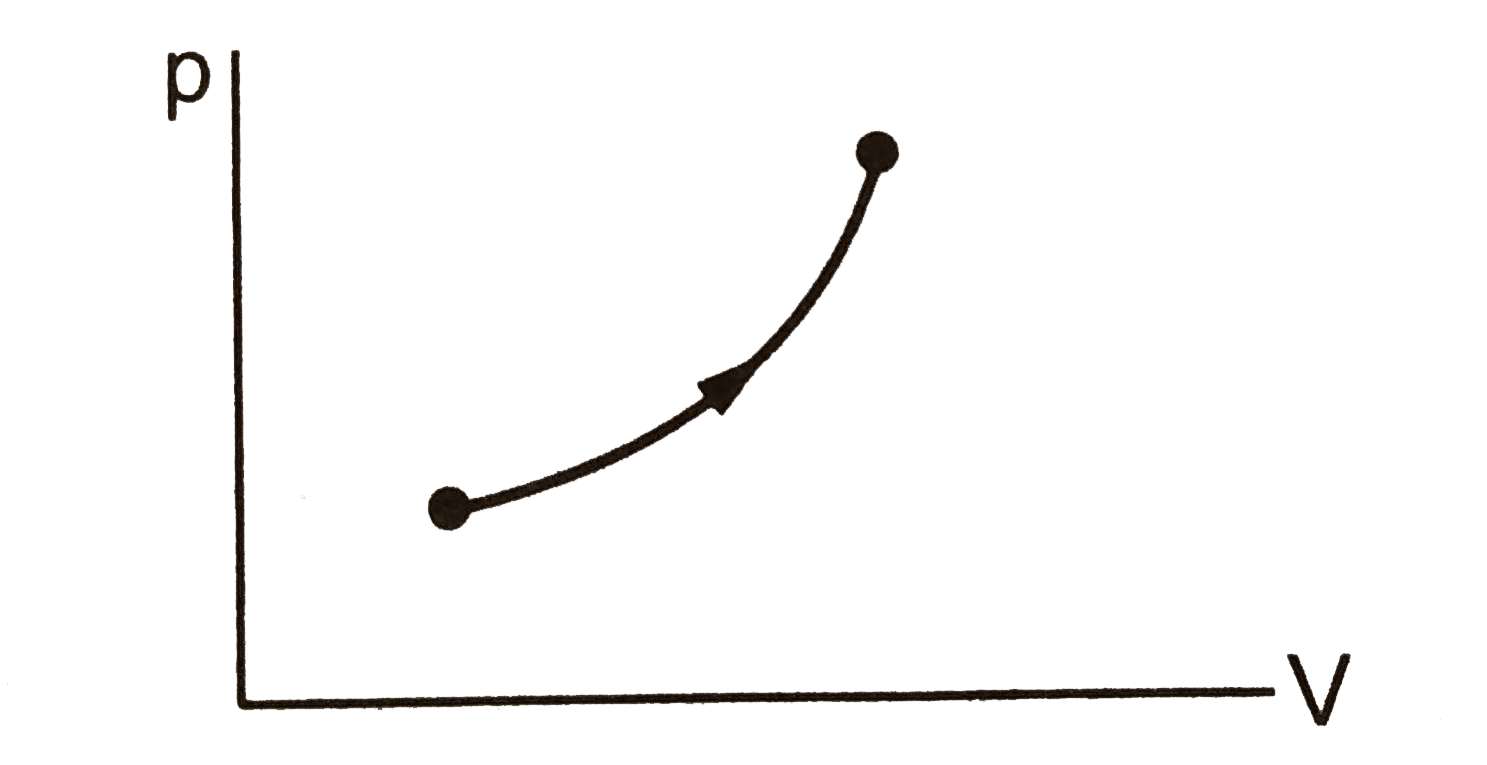
View SolutionThe molar heat capacity for the process shown in fig. is

View SolutionThe molar heat capacity for the process shown in fig. is

View SolutionIn a isothermal process on an ideal gas, the pressure increases by 0.5% . The volume decreases by about.
View SolutionIn an adiabatic process on a gas with `(gamma = 1.4)` th pressure is increased by 0.5% . The volume decreases by about
View Solutiontwo samples 1 and 2 are initially kept in the same state. the sample 1 is expanded through an isothermal process where as sample 2 through an adiabatic process up to the same final volume.Let `p_(1)` and `p_(2)` be the final pressure of the samples and 2 respectively in the previous question then.
View SolutionIn given figure, let `Delta W` and `Delta W_(2)` be the work done by the gas in process `A` and `B` respectively then (given change in volume is same in both process)
View SolutionThe molar heat capacity of oxygen gas at STP is nearly 2.5R. As the temperature is increased, it gradually increases and approaches 3.5 R. The most appropriate reason for this behaviour is that at high temperature
View SolutionA gas kept in a container of finite conductivity is suddenly compressed . The process
View SolutionLet Q and W denote the amount of heat given to an ideal gas the work done by it in an isothermal process.
View SolutionLet `Q and W` denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
View SolutionConsider the processes A and B shown in Figure (27- Q3 ) It is possible that (fig.)

View SolutionThree identical adiabatic containers `A, B and C` Contain helium, neon and oxygen respectively at equal pressure. The gases are pushed to half their original volumes. (initial temperature is same)
View SolutionA rigid container of negligible heat capacity contains one mole of an ideal gas. The temperatures of the gas increases by `1^@C` if `3.0` cal of heat is added to it. The gas may be
View SolutionFour cylinders contain equal number of moles of argon, hydrogen, nitrogen and carbon dioxide at the same temperature. The energy is minimum in
View SolutionA vessel containing one of mole of a monatomic ideal gas (molecular weight = `20 g/(mol)`) is moving on a floor at a speed of `50 m s^(-1)` The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas , find the rise in its temperature .
View Solution`5g` of a gas is contained in a rigid container and is heated from `15^@C to 25^@C` . Specific heat capacity of the gas at constant volume is `0.172 cal g ^(-1)^@C^(-1)` and the mechanical equivalent of heat is 4.2 J cal . Calculate the change in the internal energy of the gas.
View SolutionFigure shows a cylindrical container containing oxyegn `(gamma = 1.4)` and closed by a 50 kg frictionless piston. The area of cross section is `100cm(2)` , atmospheric pressure is `100 kPa`+E2 and g is 10 m s^(-2)`. The cylinder is slowly heated for some time. Find the amount of heat supplied to gas if the piston moves out through a distsnce of 20 cm.
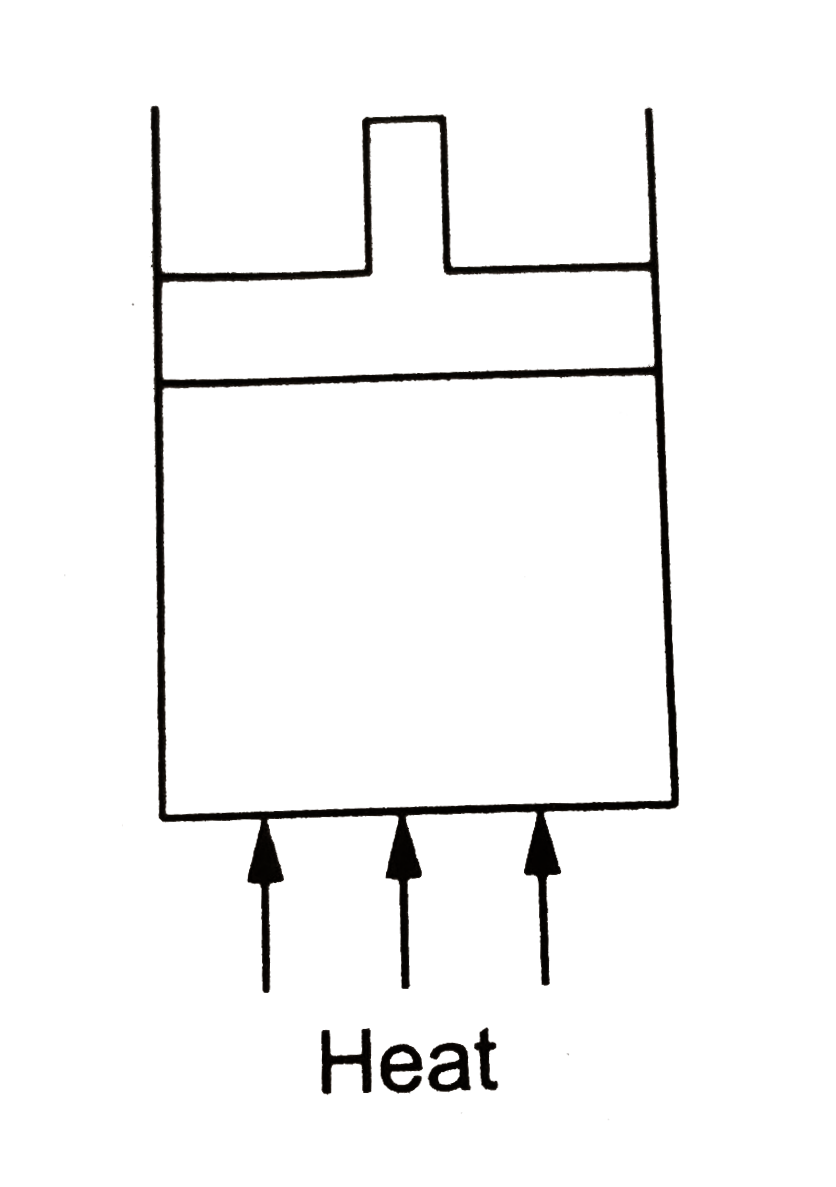 .
.
View SolutionThe specific heat capacities of hydrogen at constant volume and at constant pressure are `2.4 cal g^(-1)K ^(-1) and 3.4 cal g^(-1) K^(-1)` respectively. The molecular weight of hydrogen is `2g mol^(-1)` and the gas constant `R= 8.3 xx 10^(7)erg K^(-1) mol^(-1)` . Calculate the value of `J`.
View SolutionThe ratio of the molar heat capacities of an ideal gas is `(C_p / C_v = 7/6)`. Calculate the change in internal energy of 1.0mole of the gas when its temperature is raised by `50 K `, (a) keeping the pressure constant , (b) keeping the volume constant and (c ) adiabatically.
View SolutionA sample of air weighing `1.18 g` occupies `1.0 xx 10^(3) cm^(3)` when kept at `300 K and 1.0 xx 10^(5)` pa. When `2.0 cal` of heat is added to it constant volume, its temperature increases by `1^@C`. Calculate the amount if heat needed to increases the temperature of air by `1^@C` at constant pressure if the mechanical equivalent of heat si `4.2 xx 10^(-1)` . Assume that air behaves as an ideal gas.
View SolutionAn ideal gas expands from `100 cm^(3) to 200 cm^(3)` at a constant pressure of `2.0 xx 10^(5)` when `50 J` of heat is supplied to it. Calculate (a) the change in internal energy of the gas , (b) the number of moles in the gas if the initial temperature is 300K , (C ) the molar heat capacity `C_P` at constant pressure and (d) the molar heat capacity `C_v` at constant volume
View SolutionAn amount of heat is added to a monatomic ideal gas in a process in which the gas performs work `Q/2` on its surrounding. Find the molar heat capacity for the process.
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation `p=kv`. Show that the molar heat capacity of the gas for the process is given by `(C=C_v + ( R)/(2))`.
View SolutionAn ideal gas `(C_p // C_V = (gamma)` is taken through a process in which the pressure and the volume vary as `P = aV^b`. Find the values of (b) for which the specific heat capacity of the gas for the process is zero.
View SolutionTwo ideal gases have same value of `(C_p / C_v = gamma)`. What will be the value of this ratio for a mixture of the two gases in the ratio `(1:2)`?
View SolutionA mixture contains 1 mole of helium `(c_p = 2.5 R, C_v 1.5 R. )` and 1mole of hydrogen `(C_p = 3.5 R, C_v = 2.5 R, )` . Calculate the values of `C_p , C_v and gamma` for the mixture.
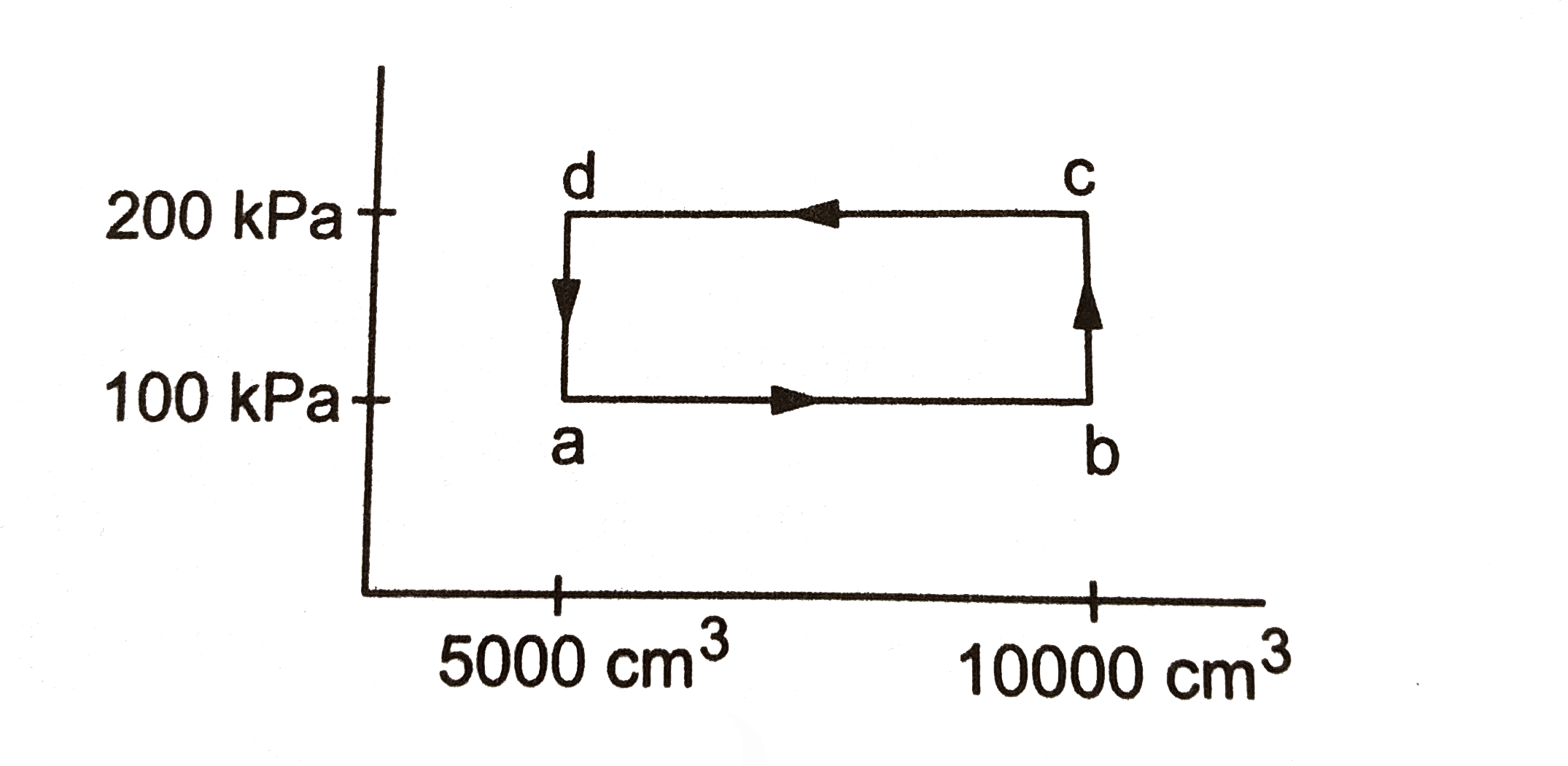
View SolutionHalf mole of an ideal gas `(gamma = 5/3)` is taken through the cycle abcda as shown in figure . Take `(R = 25/3 JK^(-1) mol^(-1))`. (a) Find the temperature of the gas in the states a, b, c and d. (b) Find the amount of heat supplied in the processes ab and bc. (c ) Find the amount of heat liberated in the processes `cd and da`.
View SolutionAn ideal gas `(gamma = 1.67 )` is taken through the process abc shown in figure . The temperature at the point a is `300 k`. Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
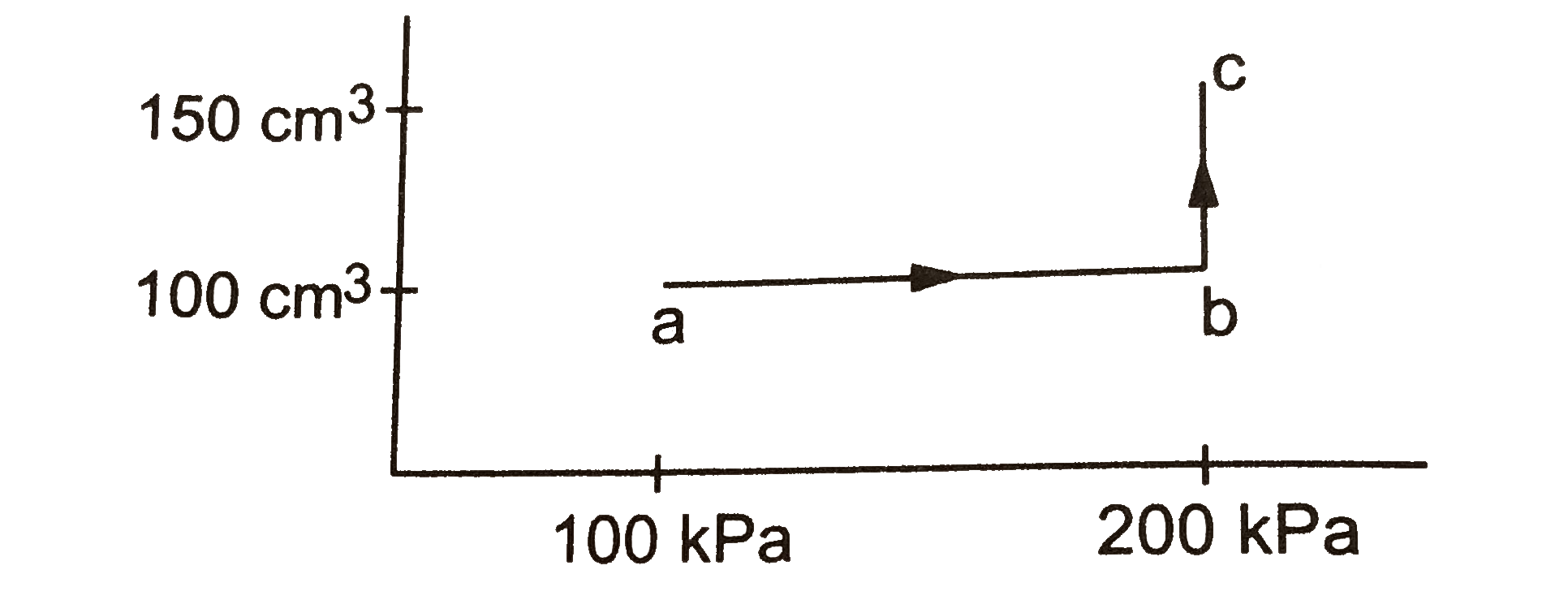
View SolutionIn Joly's differential steam calorimeter, `3g` of an ideal gas is ccontained in a rigid closed sphere at `20^@C`. The sphere is heated by steam at `100^@C` and it is found that an extra `0.095 g` of steam has condensed into water as the temperature of the gas becomes constant. Calculate the specific heat capacity of the gas in `(Jg^(-1) K^(-1).` The latent heat of vaporization of `water = 540 cal g ^(-1)`.
View SolutionThe volume of an ideal gas `(gamma = 1.5 )` is changed adiabatically from 4.00 liters to 3.00 liters . Find the ratio of (a) the final pressure to the initial pressure and (b) the final temperature to the initial temperature.
View SolutionAn ideal gas at pressure `2.5 xx 10^(5)` `pa` and temperature `300k` occupies `100`cc. It is adiabatically compressed to half its original volume. Calculate (a) the final pressure, (b) the final temperature and ( c) the work done by the gas in the process. Take `(gamma = 1.5)`.
View SolutionAir `(gamma = 1.4 )` is pumped at 2atm pressure in a motor tyre at `20^@C`. If the tyre suddenly bursts, what would be the temperature of the air coming out of the tyre. Neglect any mixing with the atmospheric air.
View SolutionA gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure , volume and temperature of the gas are `100 kPa, 400cm^(3)` and `300K` respectively. The ratio of the specific heat capacities of the gas is `(C_p / C_v = 1.5)` Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to `100 cm^(3)`.
View SolutionThe initial pressure and volume of a given mass of a gas `(C_p / C_v = gamma)` are `(p_0)` and `(V_0)`. The gas can exchange heat with surrounding. (a) It is slowly compressed to a volume `(V_0 / 2 )` and then suddenly compressed to `(V_0 /4)` . Find the final pressure. (b) If the gas is suddenly cpmpressed from the volume `(V_0 to V_0 / 2 )` and then slowly compressed to `(V_0 / 4 )`, What will be the final pressure?.
View SolutionConider a given sample of an ideal gas `(C_p / C_v = gamma )` having initial pressure `(p_0) and volume (V_0)` . (a) The gas is isothermally taken to a pressure `(P_0 / 2 )` and from there adiabatically ta a pressure `(p_0 / 2)` and from there isothermally to a pressure `(p_0 / 4 )` . find the volume.
View SolutionA given sample of an ideal gas `(gamma = 1.5 )` is compressed adiabatically from a volume of `150 cm ^(3)` to `50 cm ^(3)`. The initial pressure and the initial temperature are `150 kpa` and `300K`. Find (a) the number of moles of the gas in the sample, (b) the molar heat capacity at constant volume, (c) the final pressure and temperature, (d) the work done by the gas in the process and (e) the change in internal energy of the gas .
View SolutionThree samples A, B and C of the same gas `(gamma = 1.5)` have equal volumes and temperatures. The volume of each sample is doubled, the process being isothermal for A, adiabtic for B and isobaric for C. If the final pressures are equal for the three samples, Find the ratio of the initial pressures.
View SolutionThree samples `A`, `B` and `C` of the same gas `(gamma = 1.5)` have equal volumes and temperatures. The volume of each sample is doubled, the process being isothermal for `A`, adiabatic for `B` and isobaric for `C`. If the final pressures are equal for the three samples, Find the ratio of the initial pressures.
View SolutionFigure shows a cylindridcal tube with a adibatic walls and fitted with an adiabatic separtor. The separator can be slid into the tube by an external mechanism. An ideal gas`(gamma=1.5)` is injected in the two sides at equal pressures and temperatures . The separator remains in equilibrium at the middel. It is now slid to a position where it divides the tube in the ratio 1:3 Find the ratio of the tempertures in the two parts of the vessel.

View SolutionIn given figure, an adiabatic cylindrical tube of volume `2V_(0)` is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure `P_(1)` and temperature `T_(1)` where as in the right side having pressure `P_(2)` and temperature `T_(2).C_(p)//C_(v) =gamma` is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
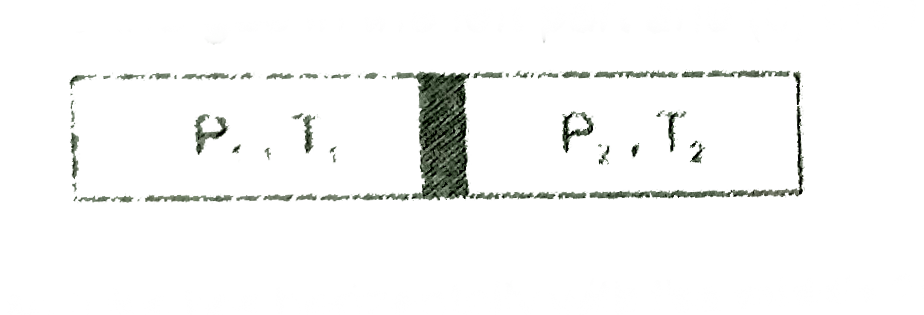
View SolutionAn adiabatic cylindrical tube of cross-sectional area `1 cm^(2)` is closed at one end fitted with a piston at the other end. The tube contains `0.03 g` of an ideal gas . At `1 atm` pressure and at the temperature of the surrounding, the length of the gas column is `40cm`.The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to `0.355 atm`. Find the speed of sound in the gas at atmospheric temperature.
View SolutionThe speed of sound in hydrogen at `0^@C` is `1280 m s^(-1)`. The density of hydrogen at STP is `0.089 kg m^(-3)`. Calculate the molar heat capacities `(C_p and C_v)` of hydrogen.
View Solution`4.0 g` of helium occupies `22400 cm^(3)` at STP. The specific heat capacity of helium at constant pressure is `( 5.0 cal K^(-1) mol ^(-1))`. Calculate the speed of sound in helium at STP.
View SolutionAn ideal gas having density `1.7 xx 10^(-3) g cm ^(-3)` at a pressure `1.5 xx 10^(5)Pa` is filled in Kundt tube. When the gas is resonated at a frequency of `3.0 KHz`, nodes are formed at a separation of `6.0 cm` . Calculate the molar heat capacites `(C_p and C_v)` of the gas.
View SolutionStanding waves of frequency `5.0 kHz` are produced in a tube filled with oxygen at `300K`. The separation between the consecutive nodes is `3.3 cm`. Calculate the specific heat capacities `(C_p and C_v)` of the gas.
View Solution
All Questions questions and complete solutions for chapter SPECIFIC HEAT CAPACITIES OF GASES of HC VERMA PHYSICS (ENGLISH) of Class 11