Complete Solutions to SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| KUMAR PRAKASHAN | SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
The displacement of a simple harmonic oscillator is given by `y= 0.40 sin (440t +0.61)`. For this, what are the value of amplitude.
View SolutionThe displacement of a simple harmonic oscillator is given by `y= 0.40 sin (440t +0.61)`. For this, what are the value of angular frequency.
View SolutionThe displacement of a simple harmonic oscillator is given by `y= 0.40 sin (440t +0.61)`. For this, what are the value of time period.
View SolutionThe displacement of a simple harmonic oscillator is given by `y= 0.40 sin (440t +0.61)`. For this, what are the value of initial phase?
View SolutionThe SHM is represented by `y= 3sin 314 t+ 4 cos 314t` y in cm and t in second. Find the amplitude of SHO.
View SolutionA particle executes SHM on a straight line path. The amplitude of oscillation is 2 cm. When the displacement of the particle from the mean position is 1 cm, the magnitude of its acceleration is equal to that of its velocity. Find the time period, maximum velocity and maximum acceleration of SHM.
View SolutionA rectangular pipe having cross-sectional area A is closed at one end and at its other end a block having same cross-section is placed so that the system is airtight. In the equilibrium position of the block, the pressure and volume of air enclosed in the pipe and P and V respectively. Prove that the block performs SHM when it is given a small displacement 'x' inward and released. Also find the period of this SHM. Assume the walls to be frictionless and compression of air to be isothermal.
View SolutionA body weighing 10kg has a velocity of `6 ms^(-1)`, after one second of starting from the mean position. If the time period of SHO is 6s, find the kinetic energy, potential energy and total mechanical energy of SHO.
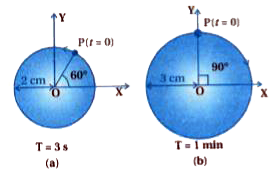
View SolutionObtain the equation for SHM of the Y-projection of the radius vector of the revolving particle P in case (a) and (b) of figure.
View SolutionThree springs are connected to a mass `m= 80 g` as shown in figure. What is the effective spring constant and periodic time, if `k= 2 Nm^(-1)`?
View SolutionA oscillator of mass 100g executes damped oscillation. When it complete 100 oscillations its amplitude of oscillation becomes half to its original amplitude. If time period is 2s, then find the value of damping coefficient.
View SolutionAmplitude of an SHO is A. When it is at a distance y from the mean position of the path of its oscillation, the SHO receives blow in the direction of its motion, which doubles its velocity instantaneously. Find the new amplitude of its oscillations.
View SolutionA simple pendulum has a length L and a bob of mass m. The bob is oscillating with amplitude A. Show that the maximum tension (T) in the string is (for small angular displacement).
`T_("max") =mg [1+(A/L)^(2)]`.
View SolutionTwo simple harmonic motions are represented by `y_(1) = 10 sin"" (pi)/(4) (12t+1)" and " y_(2) = 5(sin"" 3pi t+ sqrt(3) cos 3pi t)`. Find out the ratio of their amplitudes. What are the time period of two motions.
View SolutionFor a linear SHM, when the distance of the oscillator from the equilibrium position has values `y_(1)" and "y_(2)` the velocities are `v_(1)" and "v_(2)`. Show that the time period of oscillation is `T= 2pi [(y_(2)^(2) -y_(1)^(2))/(v_(1)^(2)-v_(2)^(2))]^(1/2)`.
View Solution
SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK) questions and complete solutions for chapter OSCILLATIONS of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 PHYSICS OSCILLATIONS
- QUESTION PAPER (SECTION - A)
- QUESTION PAPER (SECTION - B)
- QUESTION PAPER (SECTION - C)
- QUESTION PAPER (SECTION - D)
- SECTION-A (QUESTIONS- ANSWERS)
- SECTION-A (TRY YOURSELF)
- SECTION-B (ADDITIONAL EXERCISE)
- SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
- SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)
- SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
- SECTION-C (OBJECTIVE QUESTIONS ASSERTION OR REASION)
- SECTION-C (OBJECTIVE QUESTIONS FILL IN THE BLANK)
- SECTION-C (OBJECTIVE QUESTIONS MATCHING)
- SECTION-C (OBJECTIVE QUESTIONS TRUE OR FALSE)
- SECTION-C (OBJECTIVE QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION LONG ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs MORE THAN ONE OPTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs)
- SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
- SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
- SECTION-F (QUESTIONS FROM MODULE SIMPLE QUESTIONS)