Complete Solutions to SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| KUMAR PRAKASHAN | SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE) |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
Which of the following examples represent periodic motion?
View SolutionWhich of the following examples represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
View SolutionWhich of the following examples represent periodic motion?
A hydrogen molecule rotating about its center of mass.
View SolutionWhich of the following examples represent periodic motion?
An arrow released from a bow.
View SolutionWhich of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
View SolutionWhich of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
View SolutionWhich of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
View SolutionWhich of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
View SolutionFig. 14.23 depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion) ?
View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (`omega` is any positive constant):
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi//4-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat`
(e) `exp(-omega^(2)t^(2))`
(f) `1+omegat+omega^(2)t^(2)`
View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (`omega` is any positive constant):
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi//4-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat`
(e) `exp(-omega^(2)t^(2))`
(f) `1+omegat+omega^(2)t^(2)`
View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (`omega` is any positive constant):
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi//4-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat`
(e) `exp(-omega^(2)t^(2))`
(f) `1+omegat+omega^(2)t^(2)`
View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (`omega` is any positive constant):
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi//4-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat`
(e) `exp(-omega^(2)t^(2))`
(f) `1+omegat+omega^(2)t^(2)`
View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (`omega` is any positive constant):
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi//4-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat`
(e) `exp(-omega^(2)t^(2))`
(f) `1+omegat+omega^(2)t^(2)`
View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (`omega` is any positive constant):
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi//4-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat`
(e) `exp(-omega^(2)t^(2))`
(f) `1+omegat+omega^(2)t^(2)`
View SolutionA particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
at the end A.
View SolutionA particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
at the end B.
View SolutionA particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
at the mid-point of AB going towards A.
View SolutionA particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
at 2 cm away from B going towards A.
View SolutionA particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
at 3 cm away from A going towards B.
View SolutionA particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
at 4 cm away from B going towards A.
View SolutionWhich of the followng relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
`a= 0.7x`.
View SolutionWhich of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
View SolutionWhich of the followng relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
`a= - 10x`
View SolutionWhich of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function,
`x(t)=Acos(omegat+phi)`.
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is `omega` cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is `pi s^(-1)`. If instead of the cosine function, we choose the sine function to describe the SHM : `x = B sin (omegat + alpha)`, what are the amplitude and initial phase of the particle with the above initial conditions.
View SolutionA spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body ?
View SolutionA spring having with a spring constant `1200 N m^(-1)` is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
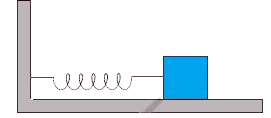
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant `1200 N m^(-1)` is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant `1200 N m^(-1)` is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionIn Exercise 9, let us take the position of mass when the spring is unstretched as x=0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t=0), the mass is at the mean position.
View SolutionIn Exercise 9, let us take the position of mass when the spring is unstretched as x=0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t=0), the mass is at the maximum streatched position.
View SolutionIn Exercise 9, let us take the position of mass when the spring is unstretched as x=0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t=0), the mass is at the maximum compressed position.
In what way to these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
View SolutionFigures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
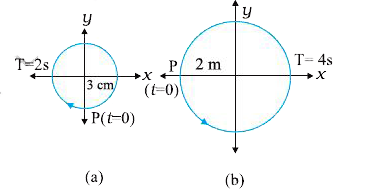
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionFigure 14.26 (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure 14.26 (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Fig. 14.26(b) is stretched by the same force F.

What is the maximum extension of the spring in the two cases ?
View SolutionThe piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed ?
View SolutionThe acceleration due to gravity on the surface of moon is `1.7 m s^(-2)`. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s ? (g on the surface of earth is 9.8 m `s^(-2)`)
View SolutionAnswer the following question :
Time period of a particle in SHM depends on the force constant k and mass m of the particle:
`T=2pisqrt(m/k)`. A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum?
View SolutionAnswer the following question :
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(l/g)`, Think of a qualitative argument to appreciate this result.
View SolutionAnswer the following question :
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall ?
View SolutionAnswer the following question :
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity ?
View SolutionA simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period ?
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density `p_(l)`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T=2pisqrt((hp)/(p_(1)g))`
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View Solution
SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE) questions and complete solutions for chapter OSCILLATIONS of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 PHYSICS OSCILLATIONS
- QUESTION PAPER (SECTION - A)
- QUESTION PAPER (SECTION - B)
- QUESTION PAPER (SECTION - C)
- QUESTION PAPER (SECTION - D)
- SECTION-A (QUESTIONS- ANSWERS)
- SECTION-A (TRY YOURSELF)
- SECTION-B (ADDITIONAL EXERCISE)
- SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
- SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)
- SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
- SECTION-C (OBJECTIVE QUESTIONS ASSERTION OR REASION)
- SECTION-C (OBJECTIVE QUESTIONS FILL IN THE BLANK)
- SECTION-C (OBJECTIVE QUESTIONS MATCHING)
- SECTION-C (OBJECTIVE QUESTIONS TRUE OR FALSE)
- SECTION-C (OBJECTIVE QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION LONG ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs MORE THAN ONE OPTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs)
- SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
- SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
- SECTION-F (QUESTIONS FROM MODULE SIMPLE QUESTIONS)