Complete Solutions to SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| KUMAR PRAKASHAN | SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS) |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
On an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
View SolutionOn an average a human heart is found to beat 81 times in a minute. Calculate its frequency and period.
View SolutionOn an average a human heart is found to beat 300 times in a minute. Calculate its frequency and period.
View SolutionWhich of the following functions of time represent (a) periodic and (b) non-periodic motion? Give the period for each case of periodic motion [`omega` is any positive constant].
(i) `sinomegat+cosomegat`
(ii) `sinomegat+cos2omegat+sin4omegat`
(iii) `e^(-omegat)`
(iv) `log(omegat)`
View SolutionWhich of the following functions of time represent (a) periodic and (b) non-periodic motion? Give the period for each case of periodic motion [`omega` is any positive constant].
(i) `sinomegat+cosomegat`
(ii) `sinomegat+cos2omegat+sin4omegat`
(iii) `e^(-omegat)`
(iv) `log(omegat)`
View SolutionWhich of the following functions of time represent (a) periodic and (b) non-periodic motion? Give the period for each case of periodic motion [`omega` is any positive constant].
(i) `sinomegat+cosomegat`
(ii) `sinomegat+cos2omegat+sin4omegat`
(iii) `e^(-omegat)`
(iv) `log(omegat)`
View SolutionWhich of the following functions of time represent (a) periodic and (b) non-periodic motion? Give the period for each case of periodic motion [`omega` is any positive constant].
(i) `sinomegat+cosomegat`
(ii) `sinomegat+cos2omegat+sin4omegat`
(iii) `e^(-omegat)`
(iv) `log(omegat)`
View SolutionWhich of the following functions does not indicates simple harmonic motion?
View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (`omega` is any positive constant):
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi//4-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat`
(e) `exp(-omega^(2)t^(2))`
(f) `1+omegat+omega^(2)t^(2)`
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic? Give the period for each case.
(1) `sinomegat-cosomegat`
(2) `sin^(2)omegat`
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic? Give the period for each case.
(1) `sinomegat-cosomegat`
(2) `sin^(2)omegat`
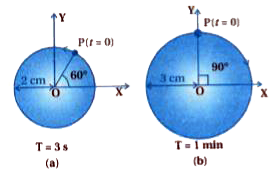
View SolutionFigures depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.
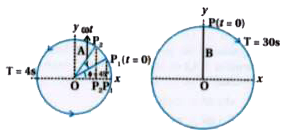
View SolutionObtain the equation for SHM of the Y-projection of the radius vector of the revolving particle P in case (a) and (b) of figure.
View SolutionA body oscillates with SHM according to the equation (in SI units),
`x = 5 cos [2pi t + pi//4]`.
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.
View SolutionA body oscillates with SHM according to the equation (in SI units),
`x = 5 cos [2pi t + pi//4]`.
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.
View SolutionA body oscillates with SHM according to the equation (in SI units),
`x = 5 cos [2pi t + pi//4]`.
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.
View SolutionA body oscillator with SHM according to the equation (in SI units)
`x= 10cos [2pi t +(pi)/(4)]`
At `t= 1.5s` calculate the displacement.
View SolutionA body oscillator with SHM according to the equation (in SI units)
`x= 10cos [2pi t +(pi)/(4)]`
At `t= 1.5s` calculate the speed.
View SolutionA body oscillator with SHM according to the equation (in SI units)
`x= 10cos [2pi t +(pi)/(4)]`
At `t= 1.5s` calculate the acceleration of the body.
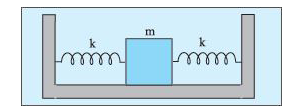
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionA block whose mass is 1kg is fastened to a spring. The spring has a spring constant of `50 Nm^(-1)`. The block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass is 2kg is fastened to a spring. The spring has a spring constant of `100 Nm^(-1)`. The block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass is 1kg is fastened to a spring. The spring has a spring constant of `50 Nm^(-1)`. The block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Calculate the kinetic, potential and total energies of the block when it is `7.07 cm` away from the mean position.
View SolutionA 5kg collar is attached to a spring of spring constant `500 Nm^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by `10.0 cm` and released. Calculate the period of oscillation.
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N `m^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N `m^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
View SolutionA 2kg collar is attached to a spring of spring constant `800 Nm^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by `10.0 cm` and released. Calculate the period of the oscillation.
View SolutionA 2kg collar is attached to a spring of spring constant `800 Nm^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by `10.0 cm` and released. Calculate the maximum speed.
View SolutionA 2kg collar is attached to a spring of spring constant `800 Nm^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by `10.0 cm` and released. Calculate maximum acceleration of the collar.
View SolutionWhat is the length of a simple pendulum, which ticks seconds ?
View SolutionHow much will the length of a simple pendulum be if its time period is 3s?
View SolutionWhat would be the length of a simple pendulum on Moon if we get its period of 2s?
View SolutionWhat will be the time period of seconds pendulum if its length is doubled?
View SolutionFor the damped oscillator, the mass m of the block is `200g, k = 90 Nm^(-1)` and the damping constant b is `40 gs^(-1)`. Calculate the period of oscillation.
View SolutionFor the damped oscillator, the mass m of the block is `200g, k = 90 Nm^(-1)` and the damping constant b is `40 gs^(-1)`. Calculate time taken for its amplitude of vibrations to drop to half of its initial value.
View SolutionFor the damped oscillator, the mass m of the block is `200g, k = 90 Nm^(-1)` and the damping constant b is `40 gs^(-1)`. Calculate the time taken for its mechanical energy to drop to half its initial value.
View SolutionFor the damped oscillator, the mass m of the block is `400g, k = 120 Nm^(-1)` and the damping constant b is `50 gs^(-1)`. Calculate the period of oscillation.
View SolutionFor the damped oscillator, the mass m of the block is `400g, k = 120 Nm^(-1)` and the damping constant b is `50 gs^(-1)`. Calculate time taken for its amplitude of vibration to drop to half of the initial value.
View SolutionFor the damped oscillator, the mass m of the block is `400g, k = 120 Nm^(-1)` and the damping constant b is `50 gs^(-1)`. Calculate time taken for its amplitude of vibration to drop to half of the initial value.
View SolutionA oscillator of mass 100g executes damped oscillation. When it complete 100 oscillations its amplitude of oscillation becomes half to its original amplitude. If time period is 2s, then find the value of damping coefficient.
View Solution
SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS) questions and complete solutions for chapter OSCILLATIONS of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 PHYSICS OSCILLATIONS
- QUESTION PAPER (SECTION - A)
- QUESTION PAPER (SECTION - B)
- QUESTION PAPER (SECTION - C)
- QUESTION PAPER (SECTION - D)
- SECTION-A (QUESTIONS- ANSWERS)
- SECTION-A (TRY YOURSELF)
- SECTION-B (ADDITIONAL EXERCISE)
- SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
- SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)
- SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
- SECTION-C (OBJECTIVE QUESTIONS ASSERTION OR REASION)
- SECTION-C (OBJECTIVE QUESTIONS FILL IN THE BLANK)
- SECTION-C (OBJECTIVE QUESTIONS MATCHING)
- SECTION-C (OBJECTIVE QUESTIONS TRUE OR FALSE)
- SECTION-C (OBJECTIVE QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION LONG ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs MORE THAN ONE OPTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs)
- SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
- SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
- SECTION-F (QUESTIONS FROM MODULE SIMPLE QUESTIONS)