Complete Solutions to SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| KUMAR PRAKASHAN | SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS) |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
A particle executes SHM along X-axis. The force acting on it is given by……….
View SolutionThe angular velocity and the amplitude of a simple pendulum is `omega` and A respectively. At a displacement x from the mean position if its kinetic energy is k and potential energy U, then the ratio of K and U is………..
View SolutionIf a simple harmonic oscillator has got a displacement of `0.02m` and acceleration eaual to `2.0 m"/"s^(2)` at any time, the angular frequency of the oscillator is equal to…….
View SolutionA simple pendulum with a bob of mass m oscillates from A to C and back to such that PB is H. If the acceleration due to gravity is g, then the velocity of the bob as it passes through B is………..

View SolutionWhich of the following is not an example of resonance?
View SolutionTime period of a simple pendulum is 2s. If its length is increased by 4 times, then its period becomes……….
View SolutionA particle performs a SHM with amplitude of `0.01m` and the frequency of its oscillation is 60 Hz. Find the maximum acceleration of a particle.
View SolutionThe equation of simple harmonic is as following `y(t) = 10 sin (20t+ 45^(@))`. Find the amplitude of SHM.
View SolutionA hollow sphere filled with water and one small hole at bottom is hung by a long thread and made to oscillates. The effect on the period of oscillation as water slowly flows out of the hole at bottom………
View SolutionDisplacement between maximum potential energy position and maximum kinetic energy position for a particle executing simple harmonic motion is……..
View SolutionThe circular motion of a particle with constant speed is……….
View SolutionThe potential energy of a long spring when stretched by 2cm is U. If the spring is stretched by 8 cm the potential energy stored in it is……….
View SolutionWhat is the phase difference the velocity and acceleration of a particle executing SHM?
View SolutionThe particle executing simple harmonic motion has a kinetic energy `K_(0)cos^(2) omega t`. The maximum value of potential energy and the total energy are respectively…………and…………..
View SolutionA mass of 2kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in figure. The mass of the spring and the pan is negligible. When spring is pressed and released the mass executes a simple harmonic motion. The spring constant is `200 N"/"m`. What should be the minimum amplitude of the motion so that the mass gets detached from the pan? (take `g= 10 m"/"s^(2)`)
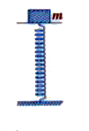
View SolutionA point performs simple harmonic oscillation of period T and the equation of motion is given by `x= a sin(omega t+(pi)/(6))`. After the elapse of what fraction of the time period, the velocity of the point will be equal to half of its maximum velocity?
View SolutionWhich one of the following equations of motion represent simple harmonic motion? Where `k, k_(0), k_(1)` and a are positive.
View SolutionA block of mass M is attached to the lower end of a vertical spring. The spring is hung from a ceiling and has force constant value k. The mass is released from rest with spring initially unstretched. The maximum extension produced in the length of the spring will be............
View SolutionThe displacement of particle along the X-axis is given by `x= a sin^(2) omega t`. The motion of the particle corresponds to………..
View SolutionA particle of mass m is released from rest and follows a parabolic path as shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time?
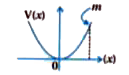
View SolutionOut of the following functions representing motion of a particle which represent SHM?
(a) `y= sin omega t- cos omega t`
(b) `y= sin^(2) omega t`
(c ) `y= 5cos ((3pi)/(4)-3 omega t)`
(d) `y= 1+ omega t+ omega^(2) t^(2)`
View SolutionTwo particle are oscillating along two close parallel straight lines side by side, with the same frequency and amplitude. They pass each other, moving on opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is.........
View SolutionWhat is the maximum speed of a particle executing SHM with amplitude of 3 cm and periodic time 6s ?
View SolutionA large horizontal surface moves up and down in SHM with an amplitude of 1 cm. If a mass of 10 kg which is placed on the surface is to remain continually in contact with it, the maximum frequency of SHM will be……….
View SolutionIf a simple pendulum oscillates with an amplitude of 50 mm and time period of 2s, then its maximum velocity is………..
View SolutionIf the period of oscillation of mass m suspended from a spring 2s, then period of mass 4 m will be….
View SolutionA particle executes simple harmonic motion with an angular velocity and maximum acceleration of `3.5(rad)/(sec)" and "7.5(m)/(s^2)` respectively. Amplitude of the oscillation is…………..
View SolutionTwo springs are connected to a block of mass M is placed on a frictionless surface as shown in figure. If both springs have a spring constant k, the frequency of oscillation of the block is………

View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic? Give the period for each case.
(1) `sinomegat-cosomegat`
(2) `sin^(2)omegat`
View SolutionA horizontal surface moves up and down in SHM with an amplitude of 1 cm. If a mass of 10 kg which is placed on the surface is remain continuously in contact with it the maximum frequency of SHM will be…………
View SolutionA particle executes SHM of period T and amplitude l along a rod AB of length 2l. The rod AB itself executes SHM of the same period and amplitude in a direction perpendicular to its length. Initially, both the particle and the rod are in their mean position. The path traced out by the particle will be...........

View SolutionA ball is suspended by a thread of length L at the point O on a wall which in indeed to the vertical by `alpha`. The thread with the ball is displaced by a small angle `beta` away from the vertical and also away from the wall. If the ball is released, the period of observation of the pendulum when `beta gt alpha` will be...........
View SolutionLet `T_(1)" and "T_(2)` be the time periods of spring A and B when mass M is suspended from the end of the spring. If both springs are taken in series and the same mass M is suspended from the series combination, the time period is T, then
View SolutionIn the equation of motion of waves in x-direction is given by `y= 10^(-4) sin(600t-2x+(pi)/(3))` where x and y are in metre and t is in second, then the velocity of wave will be…………`ms^(-1)`.
View SolutionTotal energy of SHM particle…….
View SolutionTwo springs of spring constant `k_(1)" and "k_(2)` are joined in series. Hence its equivalent spring constant of the combination is…………
View SolutionTwo simple harmonic motion are represented by the equation `y_(1)= 0.1 sin(100 pi t+(pi)/(3))` and `y_(2)= 0.1 cos pi t`. The phase difference of the velocity of particle-1 with respect to the velocity of particle-2 is…………
View SolutionThe circular motion of a particle with uniform speed is…………
View SolutionA silver atom in a solid oscillaties in simple harmonic motion in some direction with frequency of `10^((12)"/"sec)`. What is the force constant of the bonds connecting one atom with the other? (Mole wt. of silver = 108 and Avagardo number `=6.02xx 10^(23)g m "mole"^(-1)`).
View SolutionA simple harmonic motion of a particle is represented by an equation `x= 0.01 sin [100 pi (t +0.05)]`. Where x is metre and t is in second respectively. The value of time period is…………
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T. If the mass is increased by m, the time period becomes `((5)/(4)T)`. The ratio of `(m)/(M)` is...........
View SolutionA simple harmonic motion of a particle is represented by an equation `x= 5 sin(4t -(pi)/(6))`, where x is its displacement. If its displacement is 3 unit then find its velocity.
View SolutionA block of mass m be placed on a frictionless surface of a table. Spring constants of a spring joint on both side are `k_(1)" and "k_(2)` if block. Leave the block by slight displaced it, then its angular frequency will be……….
View SolutionAcceleration of a particle `a= -bx`, where x is the displacement of particle from mean position and b is constant. What is the periodic time of oscillation ?
View SolutionA mass m suspended at the end of spring of spring constant k and oscillate at periodic time T. If spring is cut into two part of equal length and tow pails are now connected in parallel and a block is suspended at the end of the combined spring and oscillate then find new periodic time.

View SolutionThe displacement of a particle performing SHM `x= 3sin 2t+4 cos 2t`. The amplitude and maximum velocity of a particle respectively are………….
View SolutionA body is moving in a room with velocity `20 m"/"s` perpendicular to the walls separated by 5 meter. There is no friction and collision with walls is elastic. The motion of body……….
View SolutionA lift is ascending with acceleration `(g)/(3)`. Find the time period of simple pendulum of length L kept in lift.
View SolutionThe ratio of maximum velocity and maximum acceleration of a particle of SHM having amplitude A and angular frequency `omega`………..
View SolutionOne fourth length of a spring of force constant k is cut away. The force constant of the remaining spring will be what ?
View SolutionA simple pendulum suspended from the ceiling of a stationary van, has time period T. If then van stats moving with a uniform velocity, the periodic of the pendulum will be………..
View SolutionA mass executes a simple harmonic motion of average potential energy `lt U gt` and average kinetic energy `lt E gt` over one time period are related to………..
View SolutionFor frequency of spring oscillator make doubly………
View SolutionThe displacement of SHM particle is `x(t)= A cos (omega t+ phi)`. Its initial displacement is 1 cm and initial velocity is `pi(cm)/(sec)` and angular frequency is `pi s^(-1)`. Find amplitude.
View SolutionA simple pendulum is taken from the equator to the pole. Its period………..
View SolutionWhen the kinetic energy of the body executing SHM is `(1)/(3)` of potential energy, the displacement is………….% of amplitude.
View SolutionThe oscillation of a body on a smooth horizontal surface is represented by the equation `x= A cos omega t` where x = displacement at time t, `omega=` frequency of oscillation. Which of the following graphs shows the corrects variation of acceleration 'a' with time 't'.
View SolutionWhen two displacements represented by `y_(1)= a sin(omega t)" and "y_(2)= b cos (omega t)` are superimposed the motion is…….
View SolutionA particle is executing SHM along a straight line. Its velocities at distance `x_(1)" and "x_(2)` form the mean position are `v_(1)" and "v_(2)`, respectively. Its time period is………..
View SolutionA particle is executing a simple harmonic motion. Its maximum acceleration is `alpha` and maximum velocity is `beta`. Then, its time period of vibration will be………
View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass when the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1 kg, the time period of oscillations becomes 5s. The value of m in kg is...........
View SolutionA spring of force constant k is cut into length of ratio `1 : 2 : 3`. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k''. That k' : k'' = …………..
View SolutionA particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in second is…….
View SolutionA pendulum is hung from the rod of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is `20 m"/"s^(2)` at a distance of 5 m from the mean position. The period of oscillation is...........
View SolutionA particle executes simple harmonic with an amplitude of 5 cm. When the particle is at 4 cm from the mean position the magnitude of its velocity in SI units is equal to that of its acceleration. Then, its periodic time in seconds is
View SolutionA cylindrical plastic bottle of negligible mass is filled with 310 ml of water and left floating in a pond with still water. If pressed downward slightly and released in starts performing simple harmonic motion at angular frequency `omega`. If the radius of the bottle is 2.5 cm then `omega` is close
View Solution
SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS) questions and complete solutions for chapter OSCILLATIONS of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 PHYSICS OSCILLATIONS
- QUESTION PAPER (SECTION - A)
- QUESTION PAPER (SECTION - B)
- QUESTION PAPER (SECTION - C)
- QUESTION PAPER (SECTION - D)
- SECTION-A (QUESTIONS- ANSWERS)
- SECTION-A (TRY YOURSELF)
- SECTION-B (ADDITIONAL EXERCISE)
- SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
- SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)
- SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
- SECTION-C (OBJECTIVE QUESTIONS ASSERTION OR REASION)
- SECTION-C (OBJECTIVE QUESTIONS FILL IN THE BLANK)
- SECTION-C (OBJECTIVE QUESTIONS MATCHING)
- SECTION-C (OBJECTIVE QUESTIONS TRUE OR FALSE)
- SECTION-C (OBJECTIVE QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION LONG ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs MORE THAN ONE OPTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION MCQs)
- SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)
- SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
- SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
- SECTION-F (QUESTIONS FROM MODULE SIMPLE QUESTIONS)