Complete Solutions to Exercise of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMODYNAMICS |
| NARAYANA | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
An amount `Q` of heat is added to a mono atomic ideal gas in a process in which the gas performs a work `Q//2` on its surrounding. Find equation of the process.
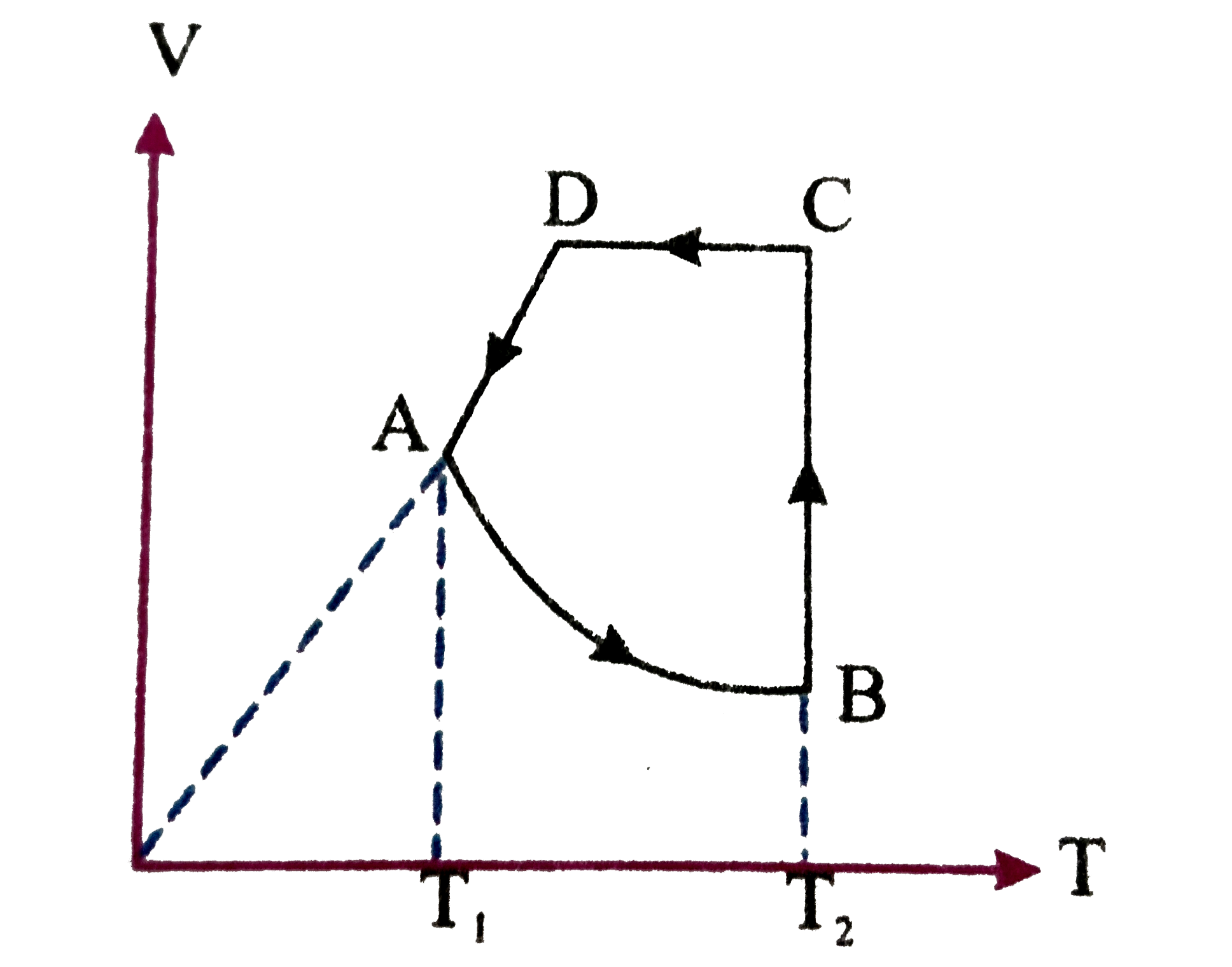
View SolutionFigure shows a cycle `ABCDA` undergone by `2` moles of an ideal diatomic gas. The curve `AB` is a rectangular hyperbola and `T_(1)=300K` and `T_(2)=500K`. Determine the work done by the gas in the process `ArarrB`.
View SolutionOne mole of an ideal monoatmic gas undergoes a process defined y `U=asqrtV` where `U` is internal energy and `V` is its volume.The molar specific heat of the gas for this process is found to be `(**)/(12)R`. The number in the numerator is not readable.What may be this number ?
View SolutionAn ideal gas can be expanded from an initial state to a certain volume through two different processes,
(I) `PV^(2)=K` and (II) `P=KV^(2)`, where `K` is a positive constant. Then, choose the correct option from the following.
View SolutionMonoatomic , diatomic and triatomic gases whose initial volume and pressure are same, each is compressed till their pressure becomes twice the initial pressure. Then:
View SolutionA cyclic process `ABCD` is shown is shown in the following `P-V` diagram. Which of the following curves represent the same process ?

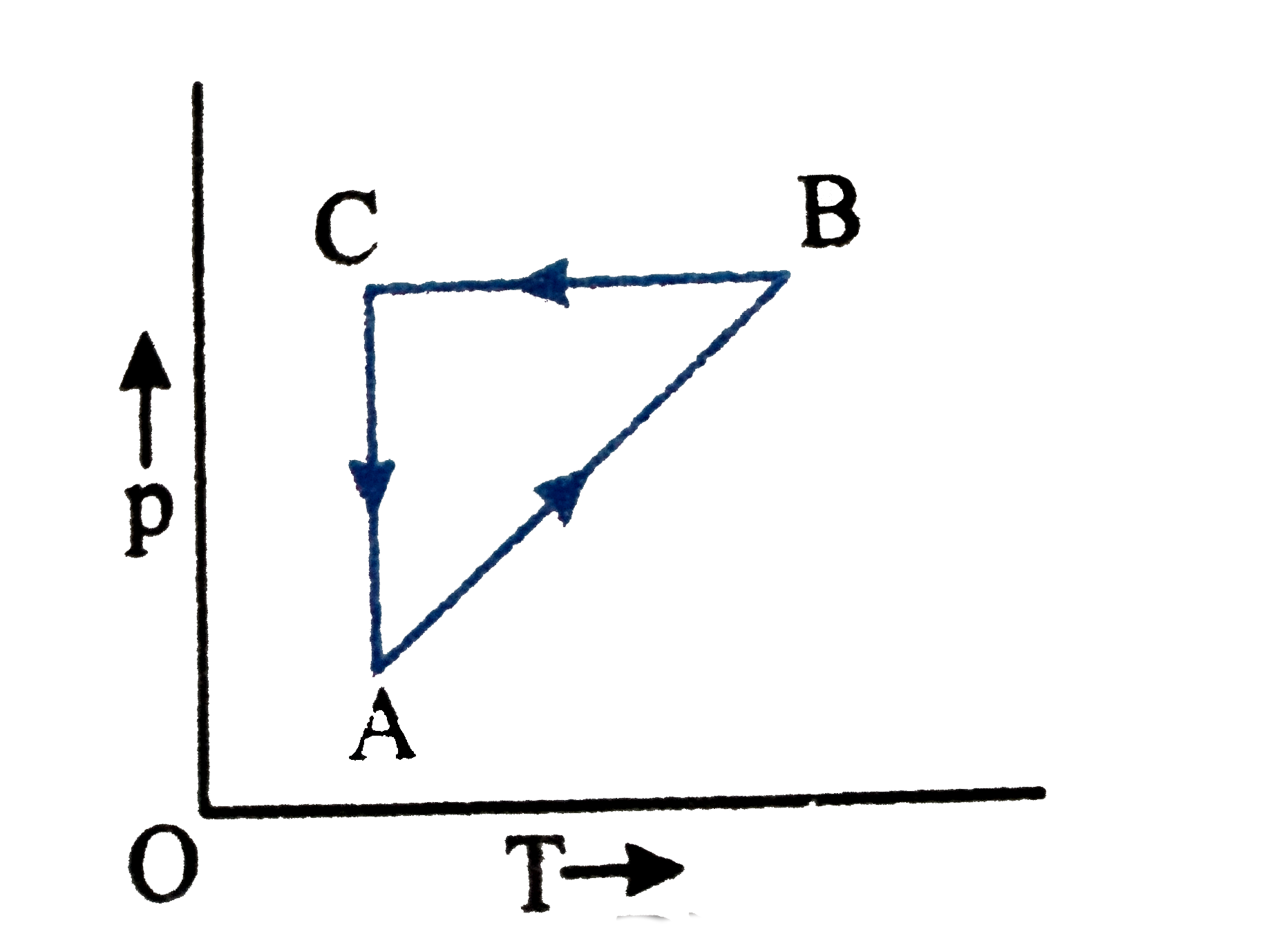
View SolutionA cyclic process is shown in the `P-T` diagram. Which of the curves show the same process on a `P-V` diagram ?
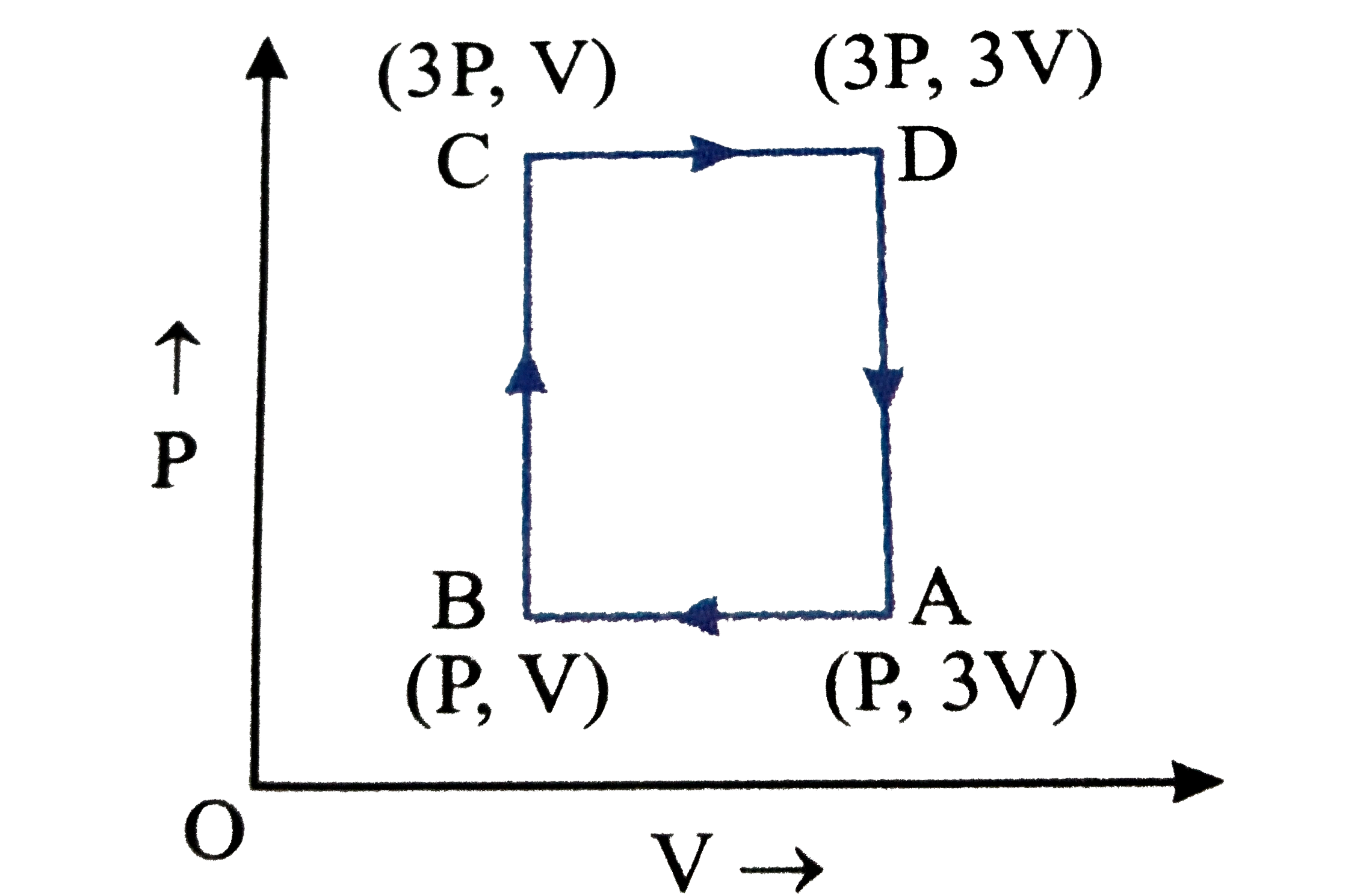
View SolutionAn ideal monoatomic gas is taken the cycle `ABCDA` as shown in following `P-V` diagram. The work done during the cycle is
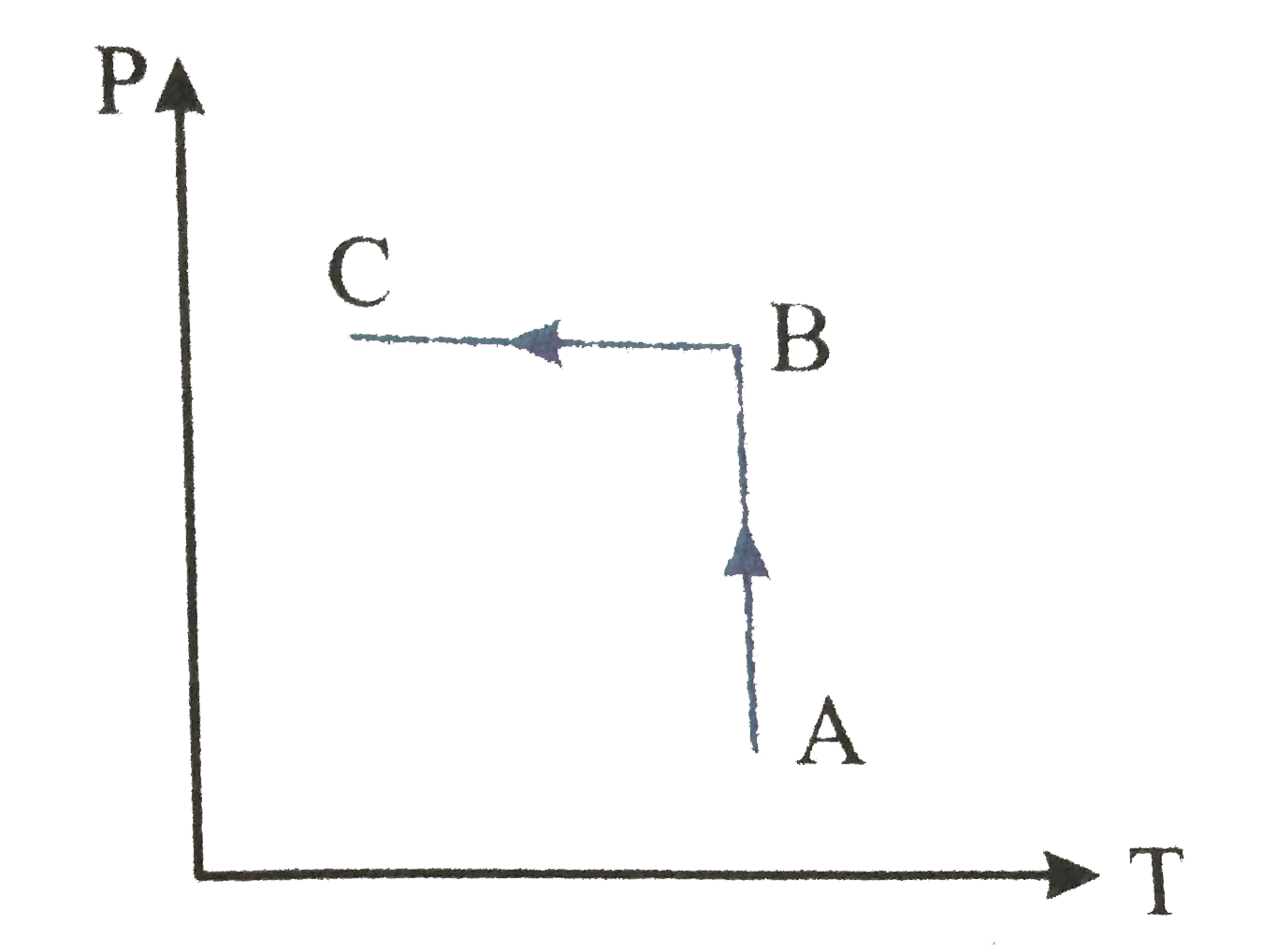
View SolutionIdeal gas is taken through the process shown in the figure :
View SolutionThe specific heat of solids at low temperatures varies with absolute temperature `T` according to the relation `S=AT^(3)`, where `A` is a constant. The heat energy required to raise the temperature of a mass m of such a solid from `T=0` to `T=20K` is:
View SolutionIn the `P-V` diagram shown shown in figure `ABC` is a semicircle.The work done in the process `ABC` is

View SolutionA thermodynamic system undergoes cyclic process `ABCDA` as shown in figure. The work done by the system is
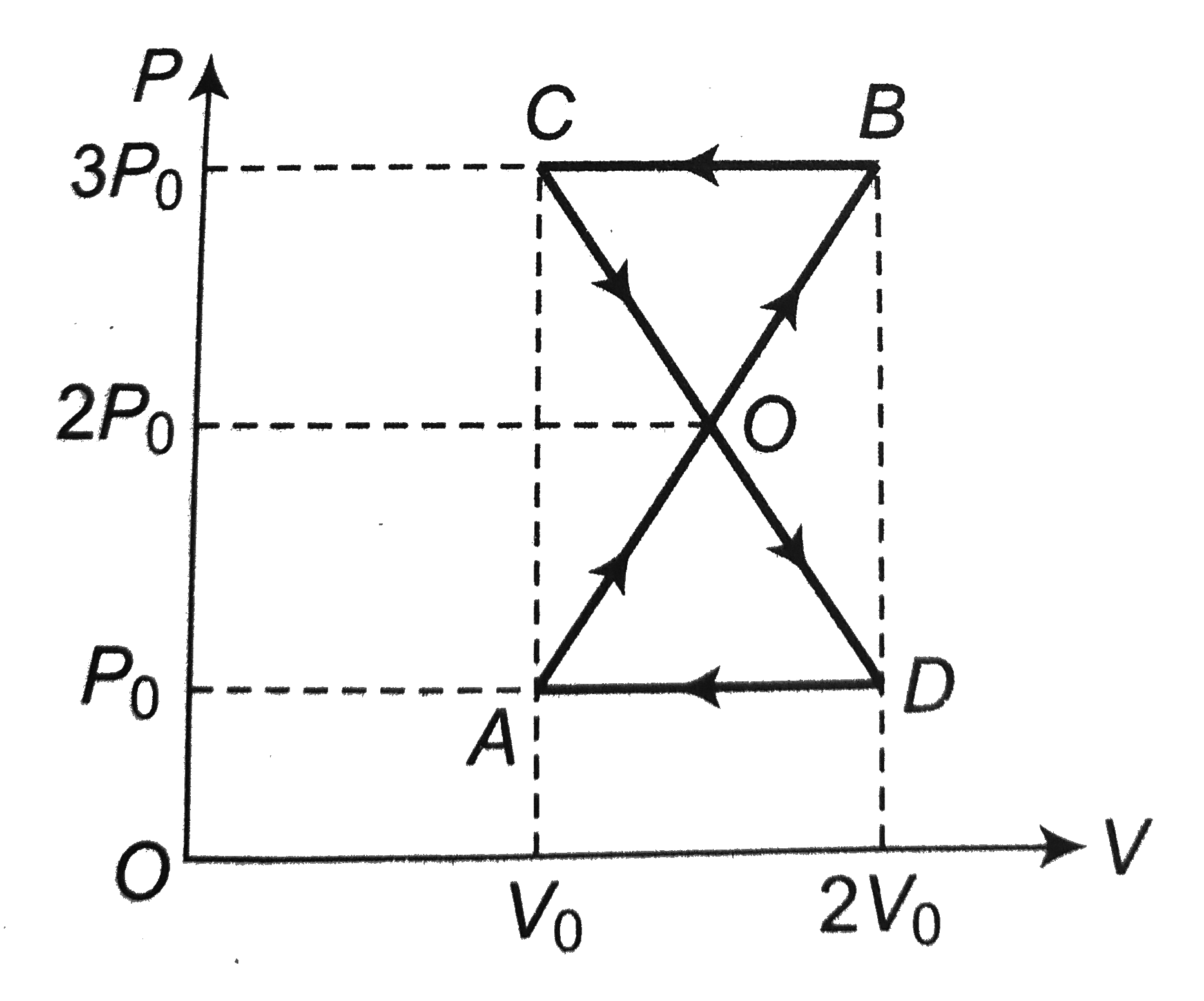
View SolutionIn a cyclic process shown in the figure an ideal gas is adial gas is adiabatically taken from `B`to`A`, the work done on the gas during the process `B`to`A` is `30,J` when the gas is taken from `A` to `B` the heat absorbed by the gas is `20 J` Then change in internat energy of the gas in the process `A` to `B` is :

View SolutionThe figure shows two paths for the change of state of a gas from A to B. The ratio of molar heat capacities in path 1 and path 2 is

View Solution`3` moles of an ideal mono atomic gas performs a cycle as shown in fig. `If` gas temperature `T_(A)=400 K` `T_(B)=800K,T_(C)=2400K`, and `T_(D)=1200K`. Then total work done by gas is
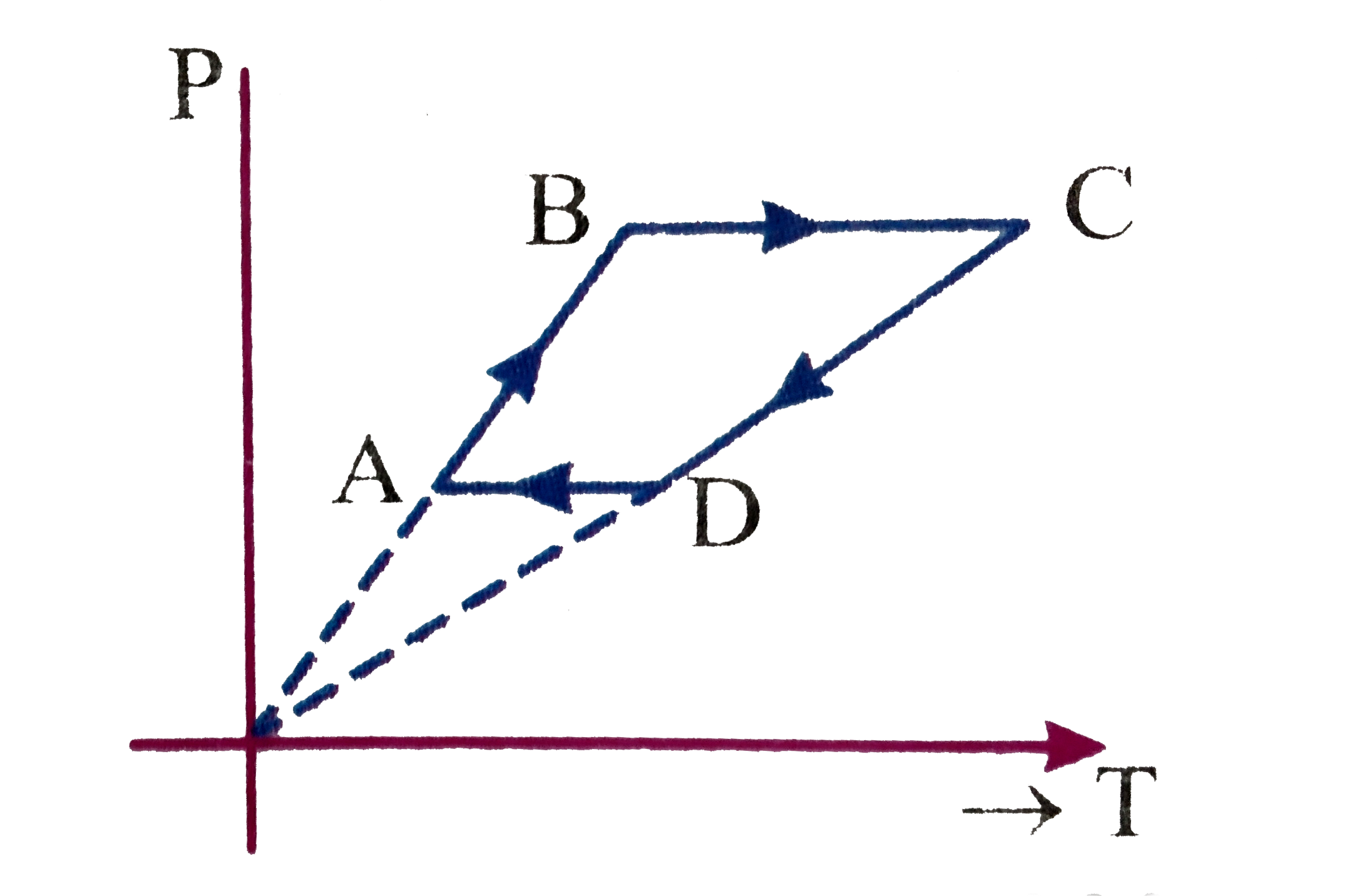
View SolutionA metal block of density `5000kg//m^(3)` and mass `2kg` in suspended by a spring of force constant `200 N//m`. The spring block system is submerged in water vessel. Total mass of water in vessel is `300 gm` and in equilibrium the block is at a height `40` cm above the bottom of vessel. The specific heat of material of block is `250J//kg//k` and that of water is `4200J//kg//k`. Neglect the heat capacities of vessel and the spring. If the support is broken the rise in temperature of water, when block reaches botton of vessel is
View SolutionOne mole of Argon undergoes a process given by `PV^(3//2)`= const. If heat obtained by gas is `Q` and molar specific of the following in the process is `C` then which of the following is correct if temperature of gas changes by `-26 K` (assusme Argon as an ideal gas)
View Solution2kg of ice at `20^@C` is mixed with 5kg of water at `20^@C` in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. It is given that the specific heats of water & ice are `1kcal//kg//^@C` and `0.5`
`kcal//kg//^@C` while the latent heat of fusion of ice is `80kcal//kg`
View SolutionSteam at `100^@C` is passed into 1.1 kg of water contained in a calorimeter of water equivalent 0.02 kg at `15^@C`till the temperature of the calorimeter and its contents rises to `80^@C` . The mass of the steam condensed in kilogram is
View SolutionA block of ice at `-10^@C` is slowly heated and converted to steam at `100^@C.` Which of the following curves represents the phenomenon qualitatively?
View SolutionPressure `P`, Volume `V` and temperature `T` of a certain material are related by the `P=(alphaT^(2))/(V)`. Here `alpha` is constant. Work done by the material when temparature changes from `T_(0)` to `2T_(0)` while pressure remains constant is :
View SolutionA closed container of volume `0.02m^3`contains a mixture of neon and argon gases, at a temperature of `27^@C` and pressure of `1xx10^5Nm^-2`. The total mass of the mixture is 28g. If the molar masses of neon and argon are `20 and 40gmol^-1` respectively, find the masses of the individual gasses in the container assuming them to be ideal (Universal gas constant `R=8.314J//mol-K`).
View SolutionIn an adiabatic process, `R = (2)/(3) C_(v)`. The pressure of the gas will be proportional to:
View SolutionThe heat supplied to one mole of an ideal monoatomic gas in increasing temperature from `T_(0)` to `2T_(0)` is `2RT_(0)`. Find the process to which the gas follows
View SolutionOne mole of monoatomic ideal gas follows a proces `AB`, as shown. The specific heat of the process is `(13R)/(6)`. Find the value of x on P-axis.

View Solution`N` moles of an ideal diatomic gas is contained in a cylinder at temparature `T`. On supplying some heat to cylinder, `(N)/(3)` moles of gas dissociated into atoms while temparature remaind constant. Heat supplied to the gas is
View SolutionAn ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the gas cycle is

View Solution5.6 liter of helium gas at STP is adiabatically compressed to 0.7 liter. Taking the initial temperature to be `T_1,` the work done in the process is
View SolutionTwo moles of ideal helium gas are in a rubber balloon at `30^@C.` The balloon is fully expandable and can be assumed to require no energy in its expansion. The temperature of the gas in the balloon is slowly changed to `35^@C.` The amount of heat required in raising the temperature is nearly (take R
`=8.31 J//mol.K`)
View SolutionOne mole of an ideal monoatomatic gas is taken round the cylic process `ABCA` as shown Then
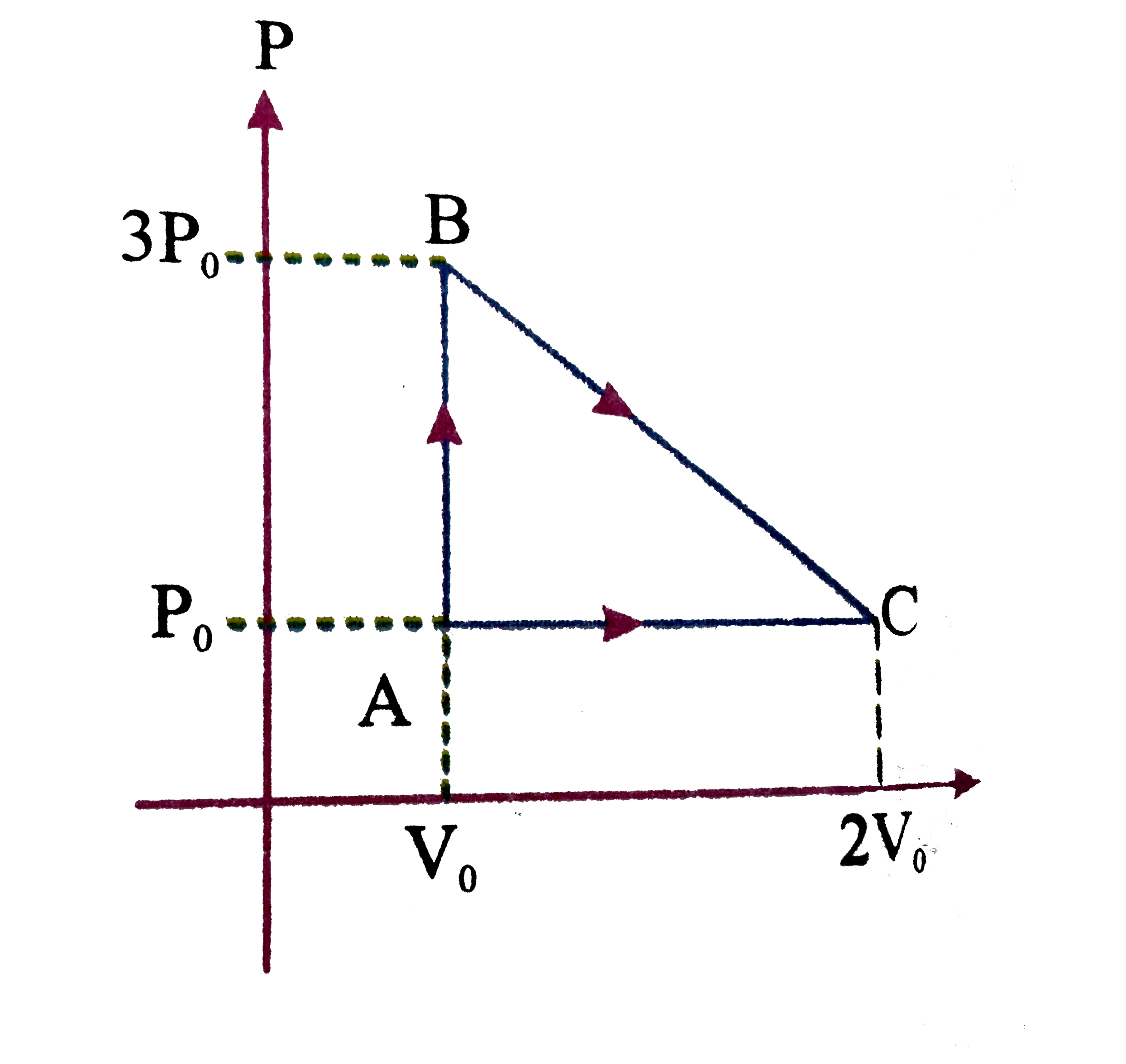
View SolutionMolar heat capacity of an ideal gas varies as `C = C_(v) +alphaT,C=C_(v)+betaV`
and `C = C_(v) + ap`, where `alpha,beta` and a are constant. For an ideal gas in terms of the variables `T` and `V`.
View SolutionAn ideal gas of mass `m` in a state `A` goes to another state `B` via three different processes as shown in Fig. If `Q_(1), Q_(2)` and `Q_(3)` denote the heat absorbed by the gas along the three paths, then

View SolutionAn ideal gas undergoes an expansion from a state with temperature `T_(1)` and volume `V_(1)` through three different polytropic processes `A, B` and `C` as shown in the `P - V` diagram. If `|Delta E_(A)|, |Delta E_(B)|` and `|Delta E_(C )|` be the magnitude of changes in internal energy along the three paths respectively, then :

View SolutionSelect the correct alternatives for an ideal gas :
View Solution`P - V` diagram of a cyclic process `ABCA` is as shown in Fig. Choose the correct alternative

View SolutionFigure shows the `P-V` siagram of a cyclic process. If `dQ` is the heat energy supplied to the system, `dU` is change in the internal energy of the system and `dW` is the work done by the system, then which of the following relations is/are correct
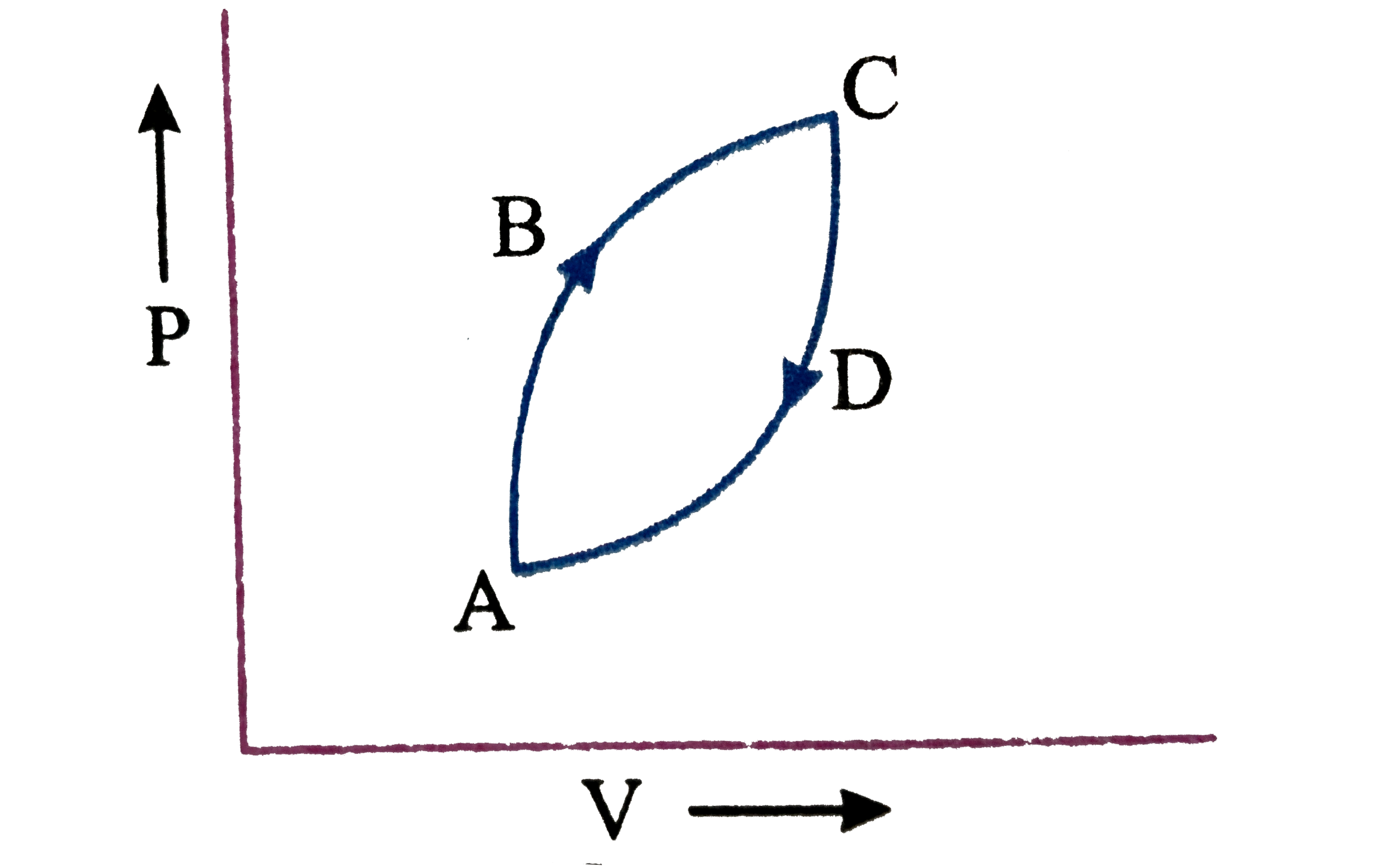
View SolutionTwo gases have the same initial pressure, volume and temperature. They expand to the same final volume, one adiabatically and the other isothermally
View SolutionDuring the process `AB` of an ideal gas

View Solution`1` kg of ice at `0^(@)C` is mixed with `1.5` kg of water at `45^(@)C` [latent heat of fusion = `80` cal//gl. Then
View SolutionIn a thermodynamic process helium gas obeys the law `TP^(2//5)` = constant,If temperature of `2` moles of the gas is raised from `T` to `3T`, then
View Solution`A` gas is found to obey the law `P^(2)V`= constant. The initial temperature and volume are `T_(0)` and `V_(0^(@))` If the gas expands to a volume `3V_(0)`, then
View SolutionThe figure shows the `P-V` plot of an ideal gas taken through a cycle `ABCDA`. The part `ABC` is a semi-circle and `CDA` is half of an ellipseThen

View Solution`C_v and C_p` denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionAn ideal gas is taken from the state A (pressure p, volume V) to the state B (pressure `p/2`, volume 2V) along a straight line path in the p-V diagram. Select the correct statement(s) from the following.
View SolutionDuring the melting of a slab of ice at 273K at atmospheric pressure,
View SolutionOne mole of an ideal gas in initial state A undergoes a cyclic process ABCA, as shown in the figure. Its pressure at A is `P_0`. Choose the correct option (s) from the following
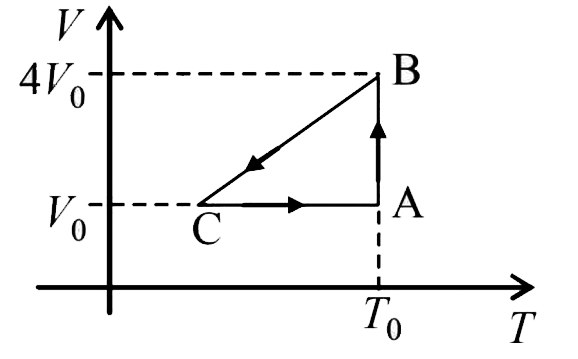
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area `A` divides the cylinder into two equal parts each with volume `V_(0)` and pressure `P_(0)` in equilibrium Assume the sepatator to move without friction.
If the piston is slightly displaced by x, the net force acting on the piston is
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area `A` divides the cylinder into two equal parts each with volume `V_(0)` and pressure `P_(0)` in equilibrium Assume the sepatator to move without friction.
Identify the correct statement
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area `A` divides the cylinder into two equal parts each with volume `V_(0)` and pressure `P_(0)` in equilibrium Assume the sepatator to move without friction.
The time period of oscillation for small displacements of the piston is
View SolutionA calorimeter of mass m contains an equal mass of water in it. The temperature of the water and clorimeter is `t_(2).A` block of ice of mass m and temperature `t_(3)lt0^(@)C` is gently dropped into the calorimeter. Let `C_(1),C_(2) and C_(3)` be the specific heats of calorimeter, water and ice respectively and `L` be the latent heat of ice.
The whole maxture in the calorimeter becomes ice if
View SolutionA calorimeter of mass m contains an equal mass of water in it. The temperature of the water and clorimeter is `t_(2).A` block of ice of mass m and temperature `t_(3)lt0^(@)C` is gently dropped into the calorimeter. Let `C_(1),C_(2) and C_(3)` be the specific heats of calorimeter, water and ice respectively and `L` be the latent heat of ice.
The whole mixture in the calorimeter becomes water if
View SolutionA calorimeter of mass m contains an equal mass of water in it. The temperature of the water and clorimeter is `t_(2).A` block of ice of mass m and temperature `t_(3)lt0^(@)C` is gently dropped into the calorimeter. Let `C_(1),C_(2) and C_(3)` be the specific heats of calorimeter, water and ice respectively and `L` be the latent heat of ice.
Water equivalent of calorimeter is
View SolutionTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area `4xx10^(-3)m^(2)`. The gas is heated by a heater for some time. During this time the gas expands and does `50J` of work in moving the piston through a distance of `0.01`m. The temperature of gas increases by `50`k.
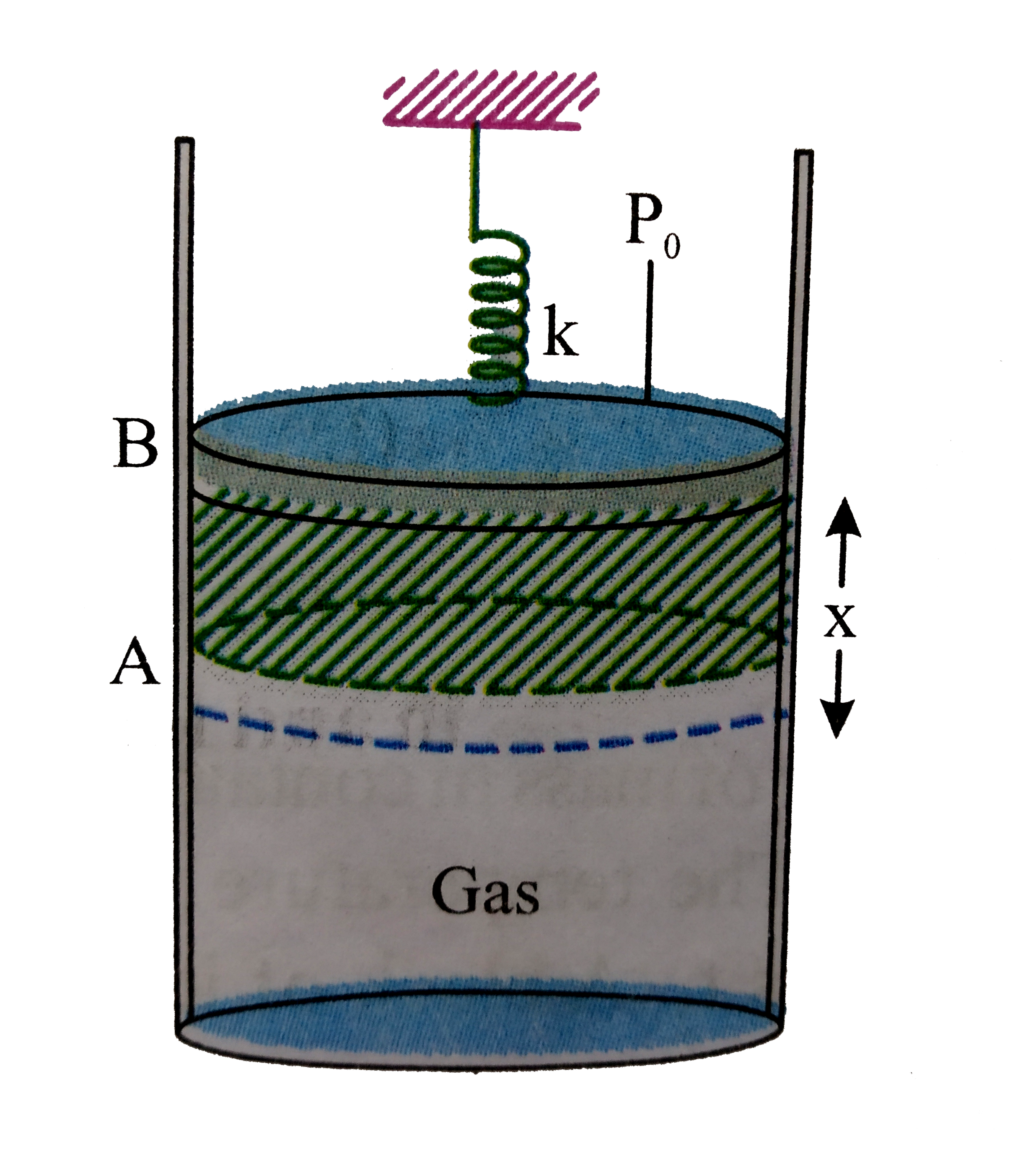
The force constant of spring is
View SolutionTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area `4xx10^(-3)m^(2)`. The gas is heated by a heater for some time. During this time the gas expands and does `50J` of work in moving the piston through a distance of `0.01`m. The temperature of gas increases by `50`k.
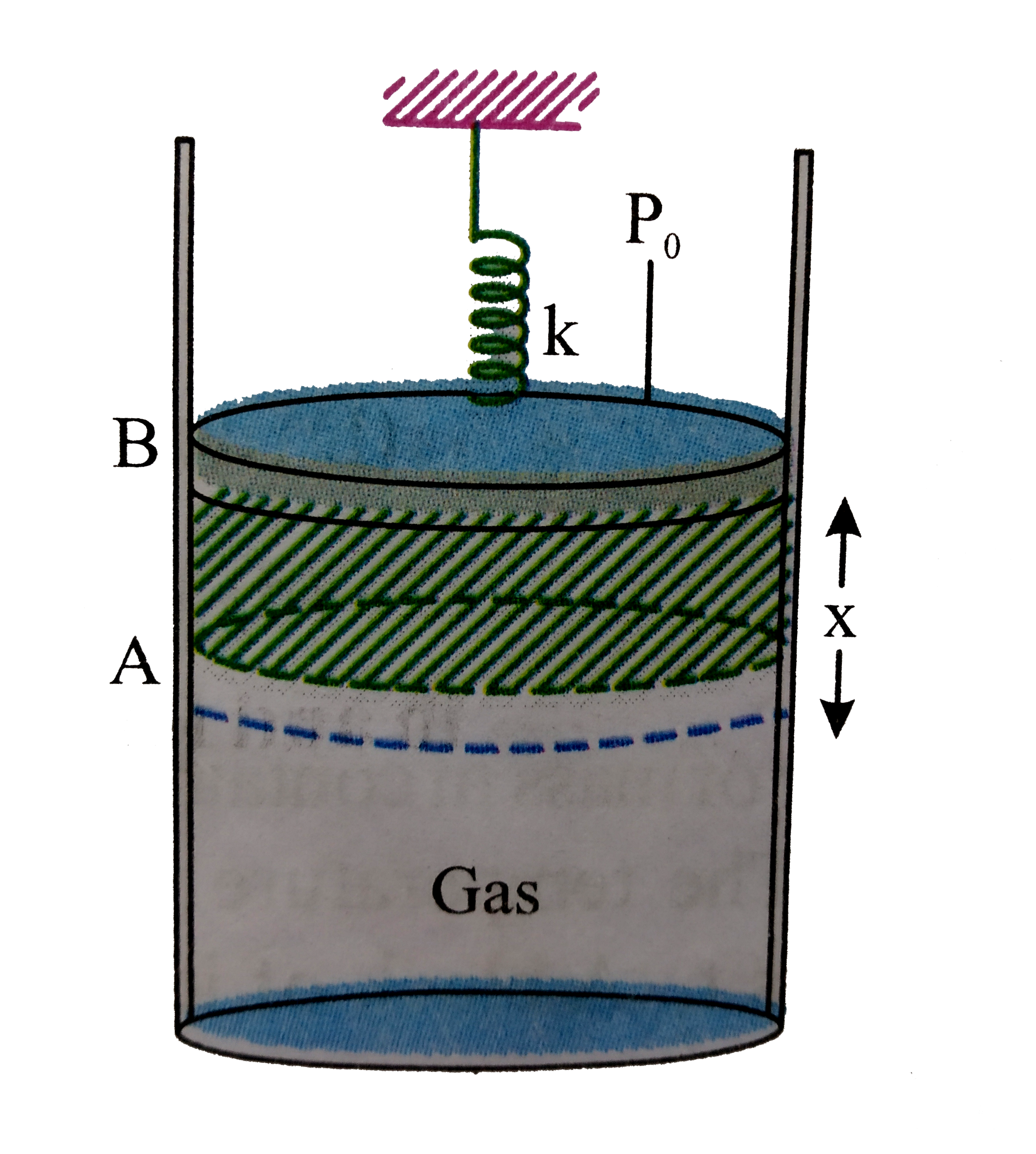
Change in internal energy of the gas is
View SolutionTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area `4xx10^(-3)m^(2)`. The gas is heated by a heater for some time. During this time the gas expands and does `50J` of work in moving the piston through a distance of `0.01`m. The temperature of gas increases by `50`k.
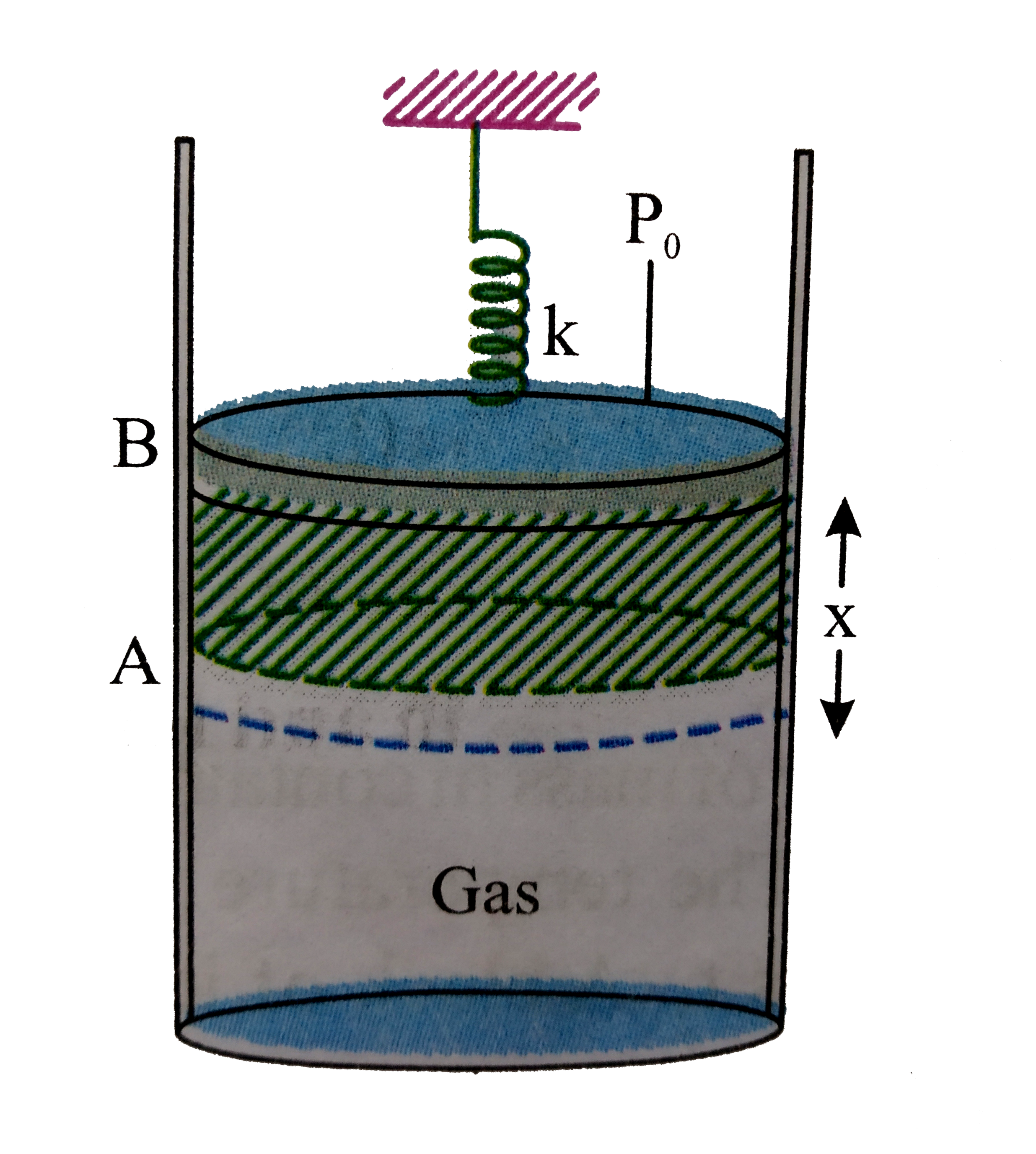
Heat supplied by heater during this process is
View SolutionA mercury barometer is defective. When an accurate barometer reads `770` mn, the defective one reads `760` mn. When the accurate one reads `750` mn, the defective one reads `742` mn. Then
The length of air coloumn when accurate barometer reads `770`mm is
View SolutionA mercury barometer is defective. When an accurate barometer reads `770` mn, the defective one reads `760` mn. When the accurate one reads `750` mn, the defective one reads `742` mn. Then
The reading of the accurate barometer, when defective are reads `752`mm is
View Solution`A 50` gm lead bullet `(sp. Heat 0.020 cal//g)` is initially at `30^(@)C` . It is fired vertically upward with a speed `84 m//s` On returning to the starting level, it strikes a slab of ice at `0^(@)C` . `(Axx100)` mg of ice is melted. Find the value of `'A'`.
View SolutionAn ideal gas `(C_p / C_v = gamma)` is taken through a process in which the pressure and volume vary as `(p = aV^(b))`. Find the value of b for which the specific heat capacity in the process is zero.
View SolutionA Vessel contains helium, which expands at constant pressure when 15 kJ of heat is supplied to it. What will be the variation of the internal energy of the gas? What is the work performed in the expansion?
View SolutionWhen a quantity of liquid bismuth at its melting point is transferred to a calorimeter containimg oil, then the temerature of oil rises from `12.5^(@)C to 27.6^(@)`. The expeiment is repeated under identical condition except that bismuth is solid, the temperature of the oil reses to `18.1^(@)C` . The specific heat of bismuth is `0.032 cal//g'C` The latent heat of fusion of bismuth is `6.7 K cal//g` .Then determine the value of `K1` Melting point of bismuth is `271^(@)C` .
View SolutionFigure shows the variation of internal energy `(U)` with the pressure `(P)` of `2.0` mole gas in cyclic process abcda.The temperature of gas at c and d are `300 and 500 K` respectively. The heat absorbed by the gas during the process is `Xxx 10 R ln 2` . Find the value of x.
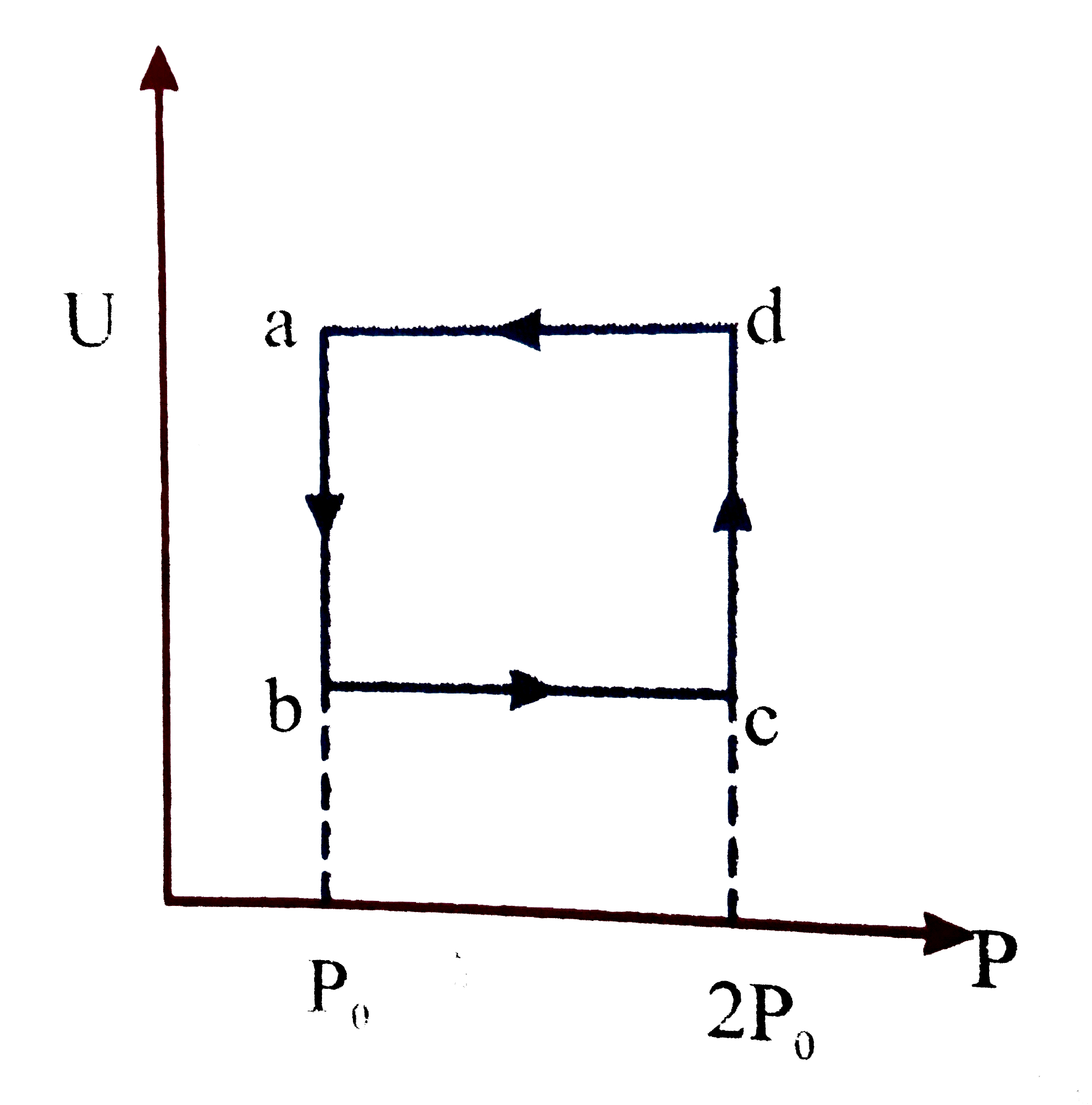
View SolutionThe heat absorbed by a system in going through the cyclic process shown shown in Fig is `xxx 5piJ` . Find the valur of x.
View Solution`1//R(R"is universal gas constant")` moles of an ideal gas `(gamma=1.5)` undergoes a cyclic process `(ABCDA)` as shown in figure. Assuming the gas to be ideal. If the net heat exchange is `10x` Joules, find the value of x ? `[In 2=0.7]`

View SolutionA metal rod AB of length 10x has its one end A in ice at `0^@C`, and the other end B in water at `100^@C`. If a point P one the rod is maintained at `400^@C`, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is `540cal//g` and latent heat of melting of ice is `80cal//g`. If the point P is at a distance of `lambdax` from the ice end A, find the value `lambda`. [Neglect any heat loss to the surrounding.]
View SolutionAn ideal diatomic gas under goes a process in which its internal energy chnges with volume as given `U=cV^(2//5)` where c is constant. Find the ratio of molar heat capacity to universal gas constant `R` ?
View SolutionAn ideal gas is taken through a cyclic thermodynamic process through four steps. The amount of heat involved in four steps are`Q_(1)=6000J,Q_(2)=-5000J,Q_(3)=5000JandQ_(4)=4000J and W=2000J`
respectively. If efficincy of cycle is `10x%` then find value of x?
View SolutionA piece of ice (heat capacity `=2100 J kg^(-1) .^(@)C^(-1)` and latent heat `=3.36xx10^(5) J kg^(-1)`) of mass m grams is at `-5 .^(@)C` at atmospheric pressure. It is given 420 J of heat so that the ice starts melting. Finally when the ice . Water mixture is in equilibrium, it is found that 1 gm of ice has melted. Assuming there is no other heat exchange in the process, the value of m in gram is
View SolutionA diatomic ideal gas is compressed adiabatically to 1/32 of its initial volume. If the initial temperature of the gas is `T_i` (in Kelvin) and the final temperature is a `T_i`, the value of a is
View SolutionWhen a system is taken from state `i` to state `f` alone the path iaf, it is found that `Q=50` cal and `W=20` cal. Along the path ibf, `Q=36` cal (figure) (a) What is `W` along the path ibf ? (b) If `W=-13` cal for the curved return path `f i`, what is `Q` for this path ? (c) Take `U_(i)=10` cal. What is `U_(f)`? (d) If `U_(b)=22` cal, what is `Q` for the process in and for the process bf ?

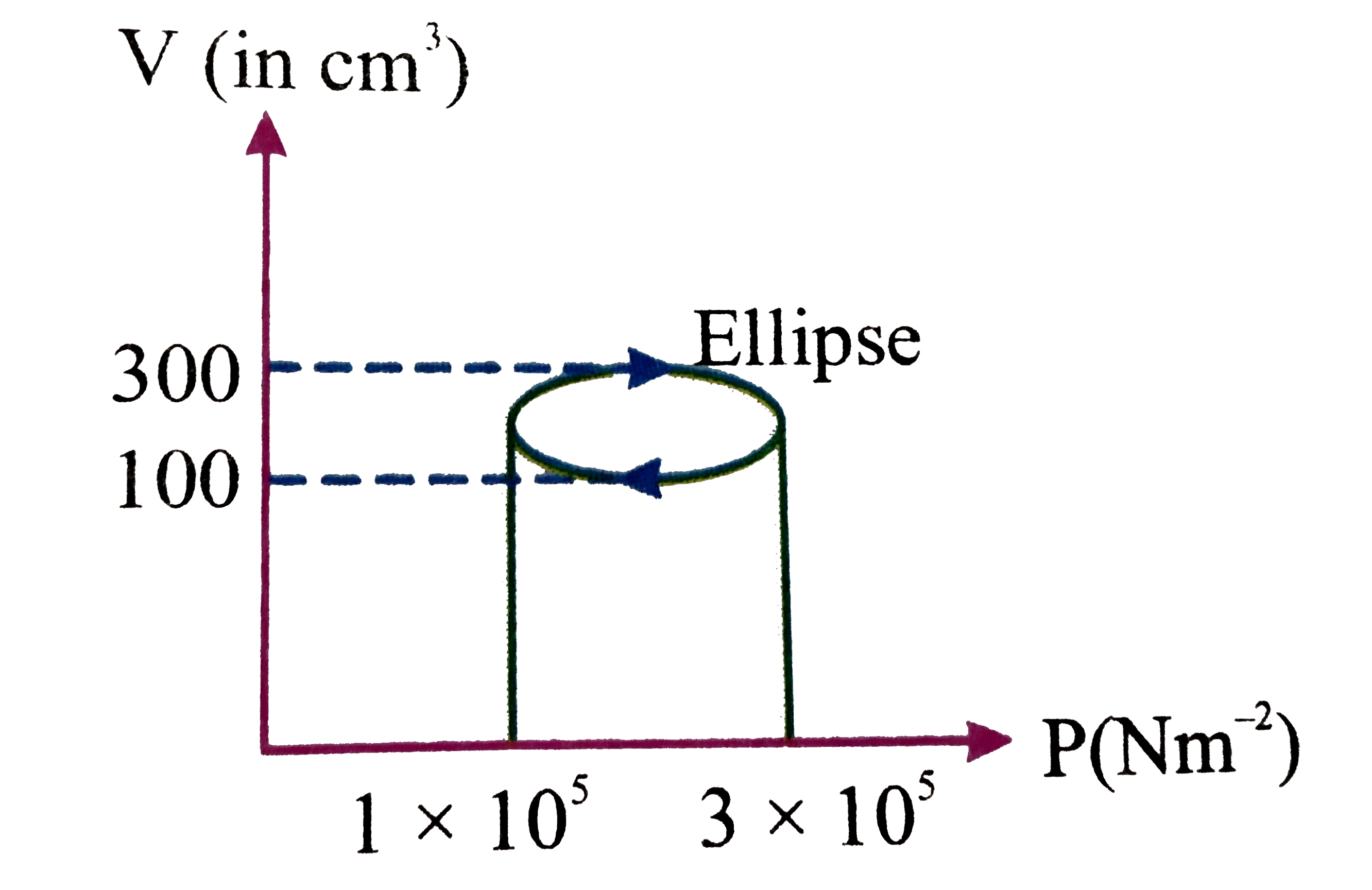
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process
(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionIn a insulated vessel, 0.05 kg steam at 373 K and 0.45 kg of ice at 253 K are mixed. Find the final temperature of the mixture (in kelvin.)
Given, `L_(fusion) = 80 cal//g = 336 J//g`
`L_("vaporization") = 540 cal//g = 2268 J//g`
`s_(ice) = 2100 J//kg.K = 0.5 cal//g.K`
and `s_("water") = 4200 J//kg.K = 1cal//g.K` .
View SolutionAn ice cube of mass 0.1 kg at `0^@C` is placed in an isolated container which is at `227^@C`. The specific heat s of the container varies with temperature T according to the empirical relation `s=A+BT`, where `A= 100 cal//kg.K and B = 2xx 10^-2 cal//kg.K^2`. If the final temperature of the container is `27^@C`, determine the mass of the container.
(Latent heat of fusion for water = `8xx 10^4 cal//kg`, specific heat of water `=10^3 cal//kg.K`).
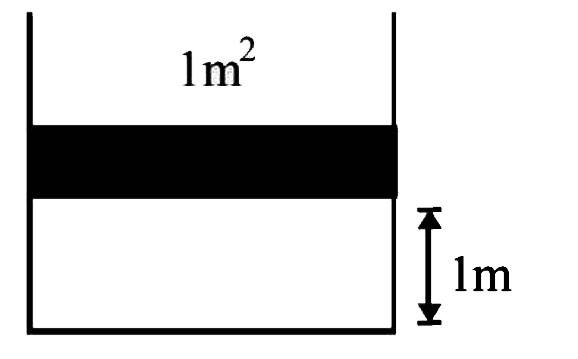
View SolutionA diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is `1m^2`. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
View SolutionTwo moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the P-T diagram. During the process AB , pressure and temperature of the gas very such that `PT=Constant`. It `T_1=300K`, calculate
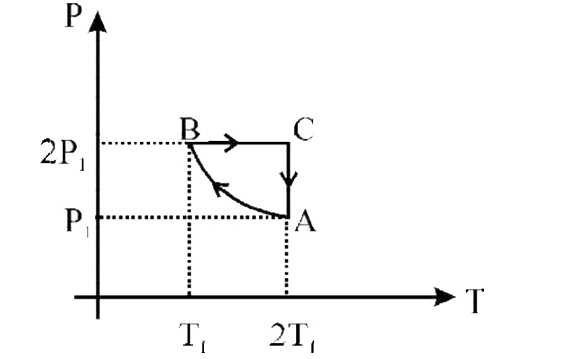
(a) the work done on the gas in the process AB and
(b) the heat absorbed or released by the gas in each of the processes. Give answer in terms of the gas constant R.
View SolutionMolar specific heat at constant volume for an ideal gas is given by `C_(v)=a+bT` (a and b are constant), `T` is temperature in Kelvin, then equation for adiabatic process is (`R`is universal gas constant)
View SolutionAn ice cube of mass `M_(0)` is given a velocity `v_(0)` on a round horizontal surface with coefficient of friction `mu`. The block is at its melting point and latent heat of fusion of ice is `L` . The block receive heat only due to the friction forces and all work is converted into heat. Find the mass of the remaining ice block after time t.
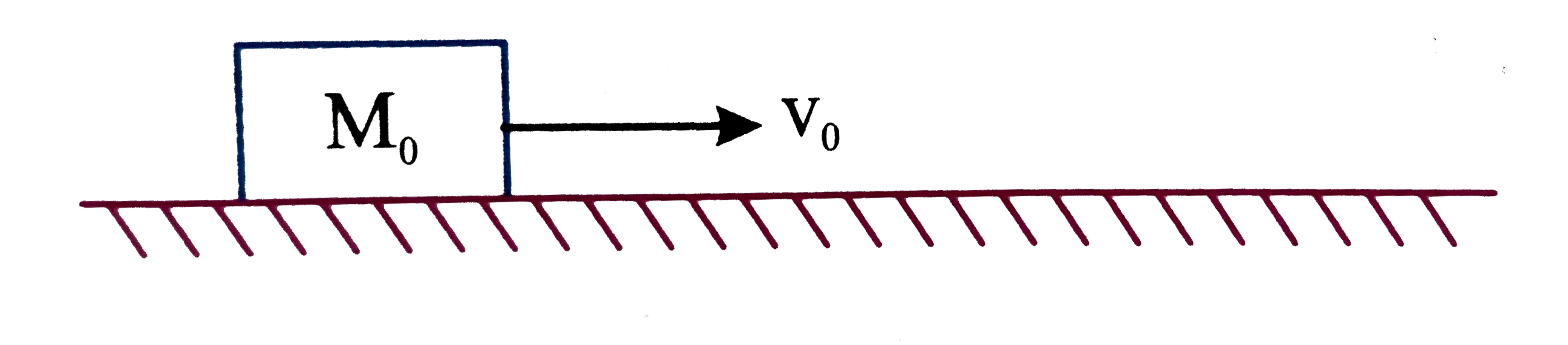
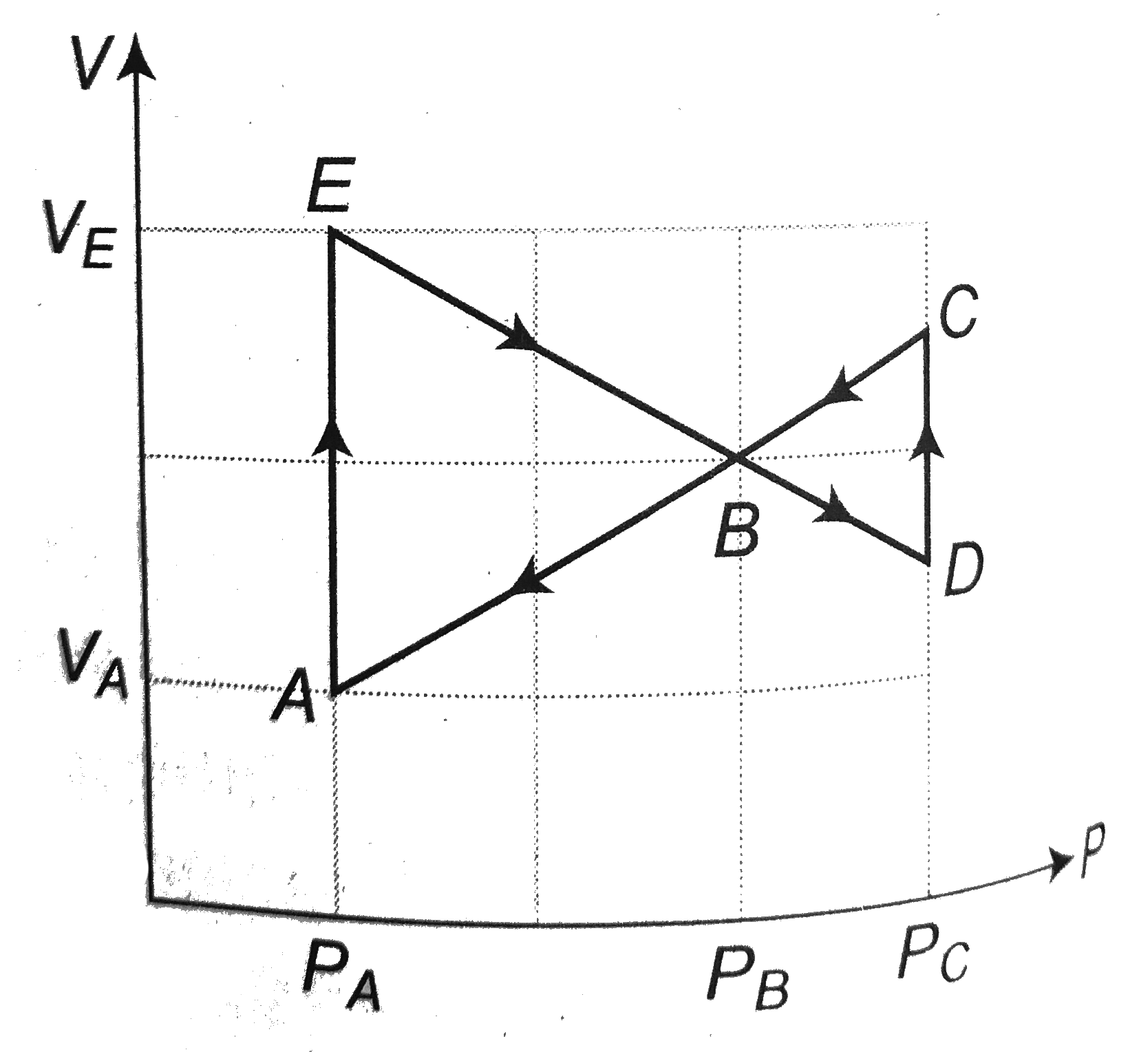
View SolutionFigure shows a cyclic process `ABCDBEA` performed on an ideal cycle. If `P_(A) = 2 atm, P_(B) = 5 atm and P_(6) = 6 atm. V_(E) - V_(A) = 20 "litre"`, find the work done by the gas in the complete, process (`1 atm. "Pressure" = 1 xx 10^(5) Pa`)
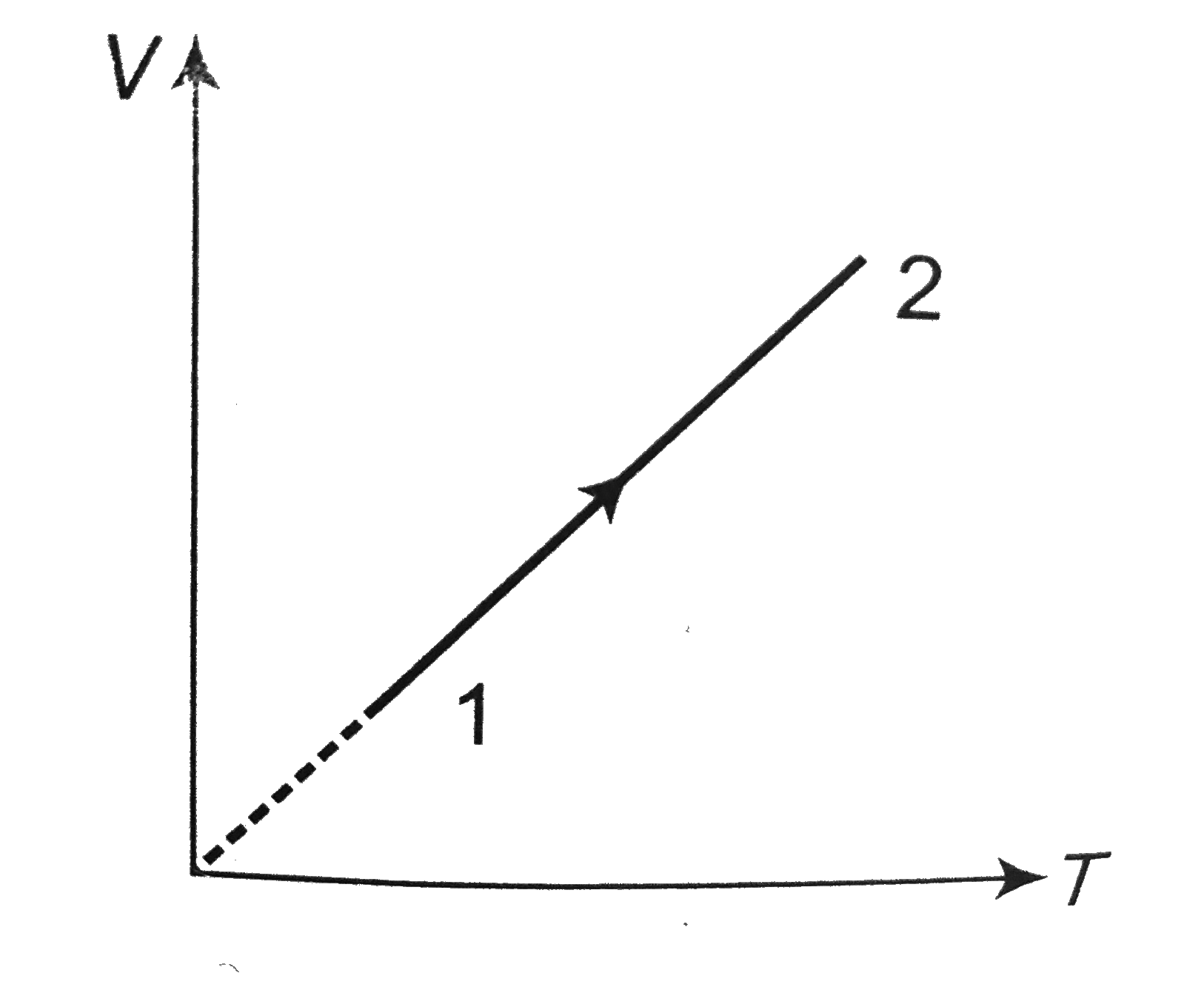
View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process `1-2` is
View SolutionAn ideal monoatomic gas undergoes a cyclic process `ABCA` as shown in the figure. The ratio of heat absorbed during `AB` to the work done on the gas during `BC` id
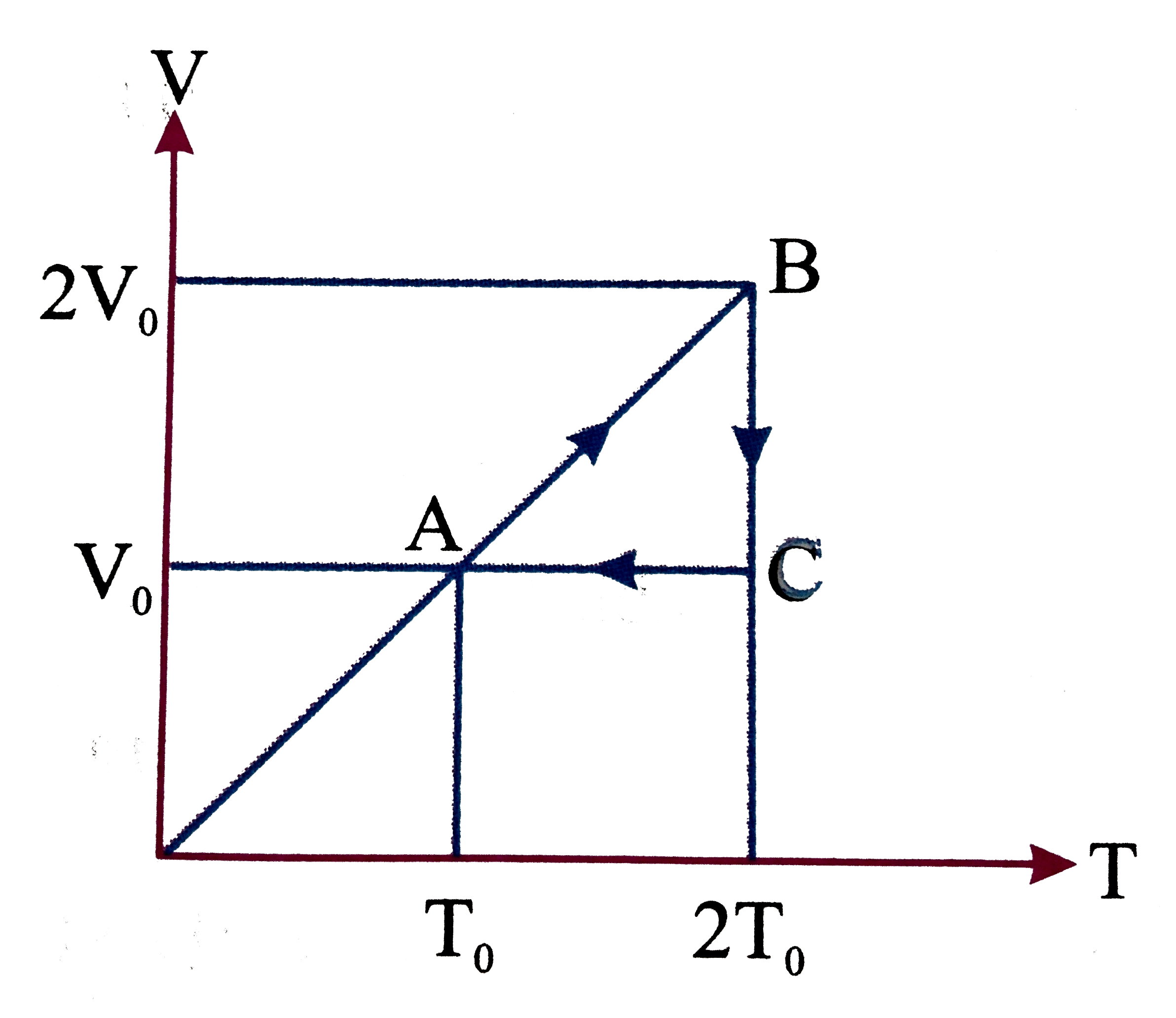
View Solution`A` vessel of water eqivalent `W` kg contains m kg of water of specific heat `S` . When water evaporates at the vessel and water of `alpha kgS^(-1)` , the temprature of the vessel and water and in it falls from `T_(1)^(@)C` to `T_(2)^(@)` in t s. If `m gt gt alpha` t and a fracrtion `E` of the heat vessel and the water then average rate of fall of temprature is
(`L=` average latent heat of vapourisation in `J kg^(-1)`)
View SolutionAn ideal gas expands isothermally from volume `V_(1)` to `V_(2)` and is then compressed to original volume `V_(1)` adiabatically. Initialy pressure is `P_(1)` and final pressure is `P_(3)`. The total work done is `W`. Then
View SolutionThe work done by a cretain material when temprature changes from `T_(0)` to `2T_(0)` m while pressure remains constant is `3betaT_(0)^(2)` where `beta` is a canstant. Draw curve between volume `(V)` and temeprature `(T)` of the material.
View SolutionAn ideal gas is made to undergo a termodynamic process given by `V prop T^(2)` , find the molar heat capacity of the gas for the above process.
View SolutionDetermine the average molar heat capacity of an ideal gas under going a process shown in fig.
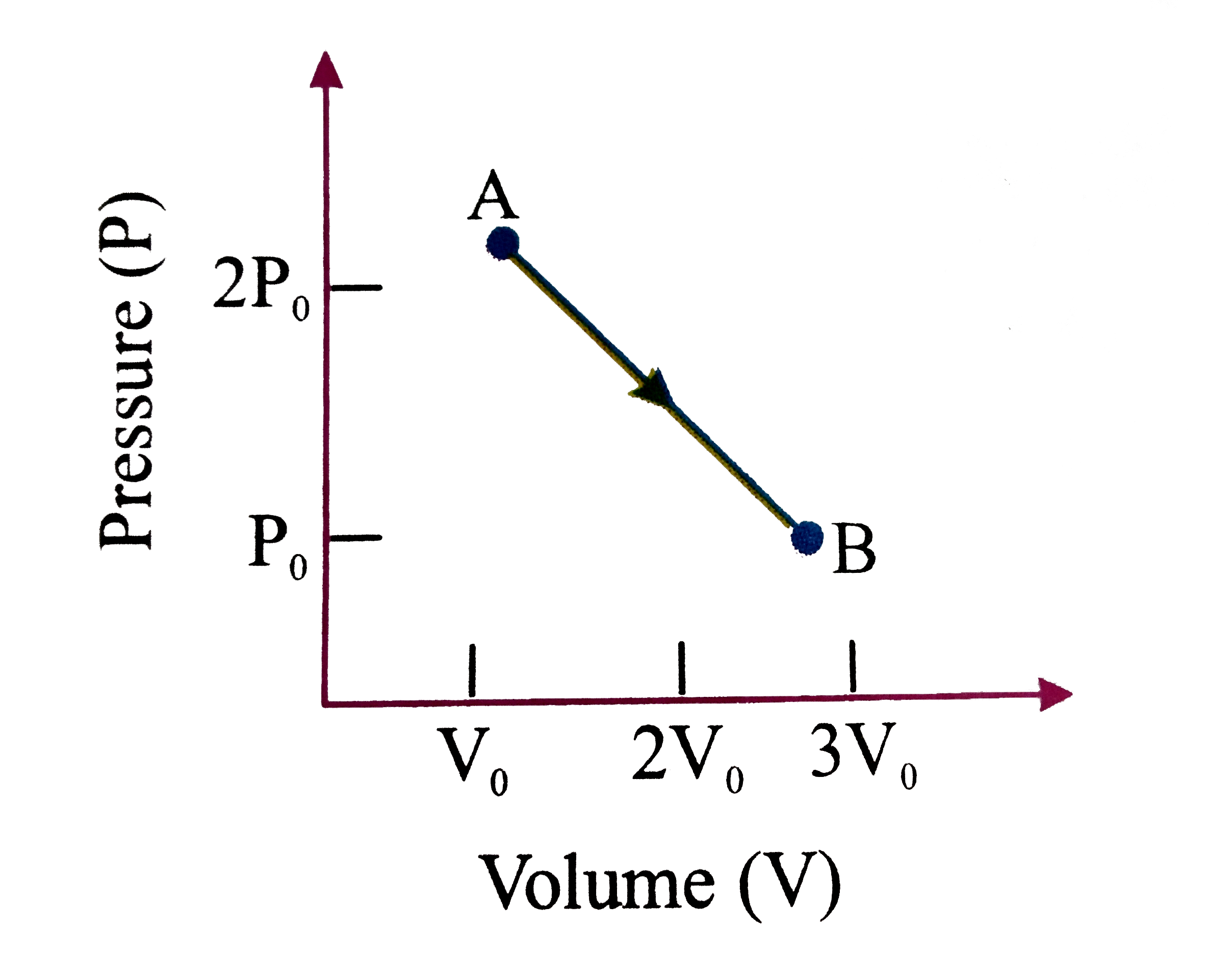
View SolutionAn ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies `K` times with tn the cycle then find out its effcincy.

View Solution`A` cycle is made of three process is iso barie, adiabatic and isothermal. Isothermal process has minimum temperature. Absolute temperature charges by `k` times withing the cycle. Find out the efficiency.
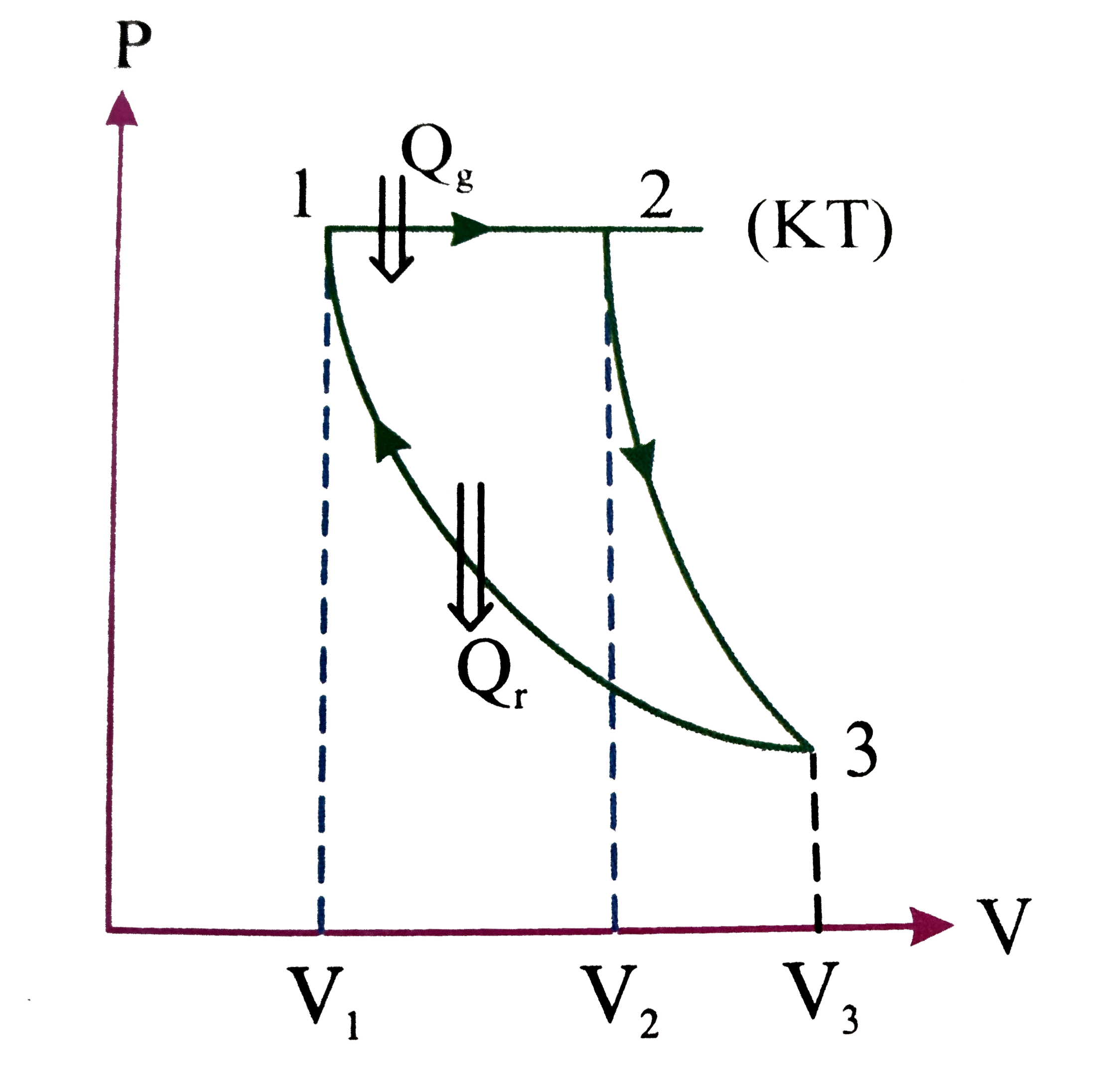
View Solution`A` calorimeter contains `4.00` kg of water at `20.0^(@)C` . What amount of ice at `-10^(@)C` , must be added to cause the resulting mixture to rach thermal equilibruim at `5.0^(@)C` . Asuume that heat transfer occurs only between the water and ice.
View Solution`A` `0.50` kg ice cube at `-10^(@)C` is placed in `3.0` kg of coffce at `20^(@)C` . What will be the final temperature of mixture? Assume that specifec heat of tea is same as that of water.
View SolutionA thermal insulated vessel contains some water at `0^(@)C`. The vessel is connected to a vaccum pump to pum out water vapour. This results in some water getting frozen. It is given latent heat of vaporization of water at `0^(@)C = 21 xx 10^(5) J//kg` and latent heat of freezing of water `=3.36 xx 10^(5) J//kg`. the maximum percentage amount of water vapour that will be solidified in this manner will be:
View SolutionIf specific heat capacity of a substance in solid and liquid is proportional to the temperature of substance, then temperature Vs time plot for the substance is best present by [Assume heat is supplied to substance at constant rate and initial temperature is less than melthing pint of substance.
View Solution`450` g water at `40^(@)C` was kept in a calorimeter of water equivalent `50 g 25 g ice at 0^(@)C` is added and simultaneously `5` g steam at `100^(@)C` was passed to the calorimeter. The final temperature of the calorimeter. Will be
`(L_(ice)=80 cal // g.L_(steam) =540cal//g)`
View Solution`5` moles of nitrogen gas are enclosed in an adiabatic cylindrical vessel. Thel piston itself is a rigid light cylindrical container containing `3` moles of helium gas. There is a heater which given out a power of `30` cal is transferred to helium through the batton surface of the piston. The rate of incremnt of temperature of the nitrogen gas assuming that the piston
moves slowly, is
View SolutionWhen water is boiled at `2` atm pressure the latent heat of vapourization is `2.2xx10^(6) J//kg` and the boiling point is `120^(@)C` At `2` atm pressure `1` kg of water has a volume of `10^(-3)m^(-3)` and `1` kg of steam has volume of `0.824m^(3)` . The increase in internal energy of `1` kg of water when it is converted into steam at `2` atm pressure and `120^(@)C` is [`1` atm pressure `=1.013xx10^(5)N//m^(2)`]
View Solution`A` vertical cylinder of cross-section area `A` contains one mole of an ideal mono-atmic gas under a piston of mass `M` At a certain instant a heater which supplies heat at the rate q `J//s` is switched `ON` under the piston. The velocity with which the piston moves upward under the condition that pressure of gas remains constant is [Assume on heat transfer through walls of cylinder]
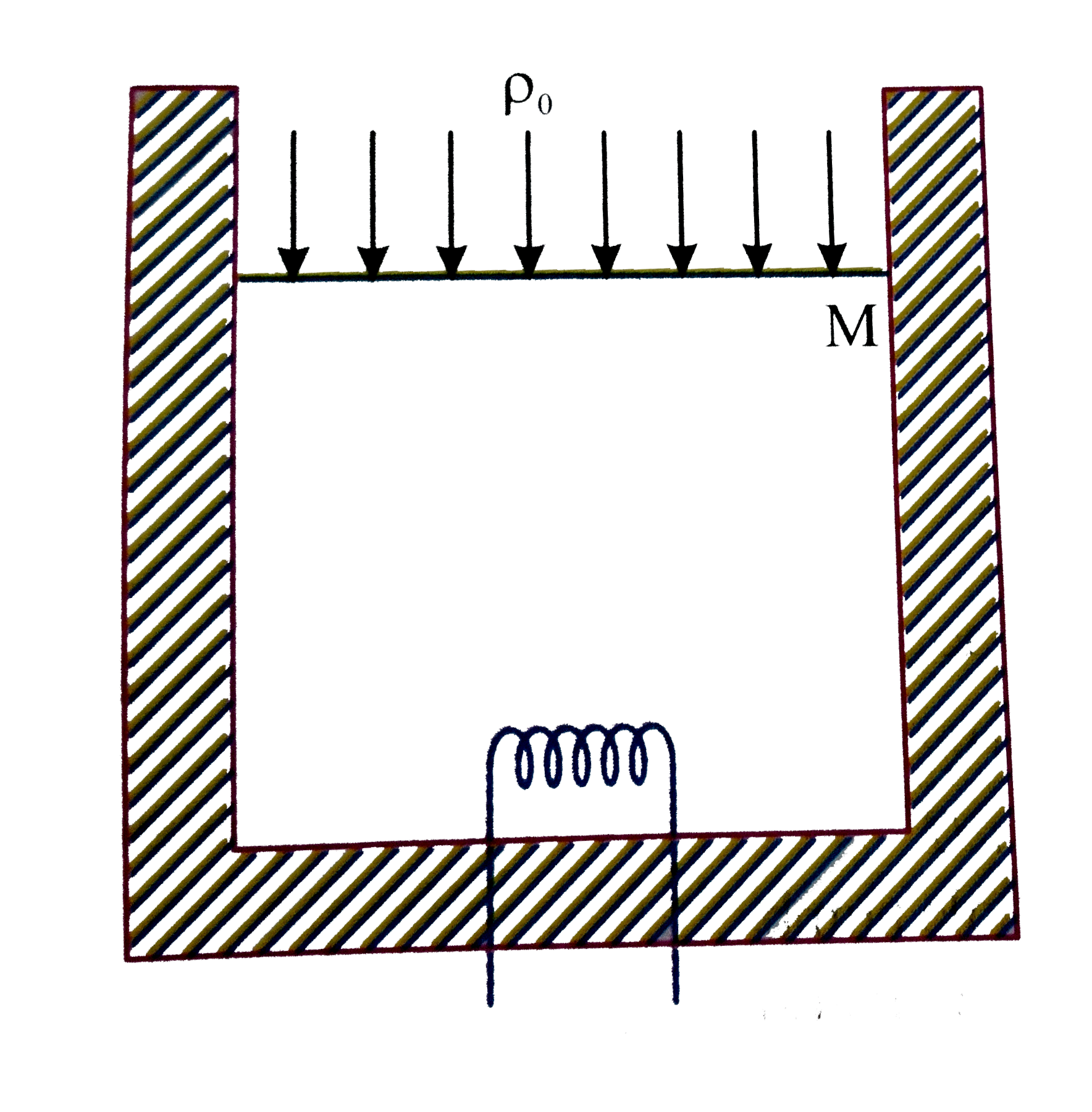
View SolutionA gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at pressure `P_i=10^5` Pa and volume `V_i=10^-3m^3` changes to a final state at `P_f=(1//32)xx10^5Pa and V_f=8xx10^-3m^3` in an adiabatic quasi-static process, such that `P^3V^3=constant.` Consider another thermodynamic process that brings the system form the same initial state to the same final state in two steps: an isobaric expansion at `P_i` followed by an isochoric (isovolumetric ) process at volume `V_r.` The amount of heat supplied to the system i the two-step process is approximately
View SolutionOne mole of an ideal monoatomaic gas is taken from `A` to `C` along the path `ABC` . The temperature of the gas at `A` is `T_(0)` . For the process `ABC` :
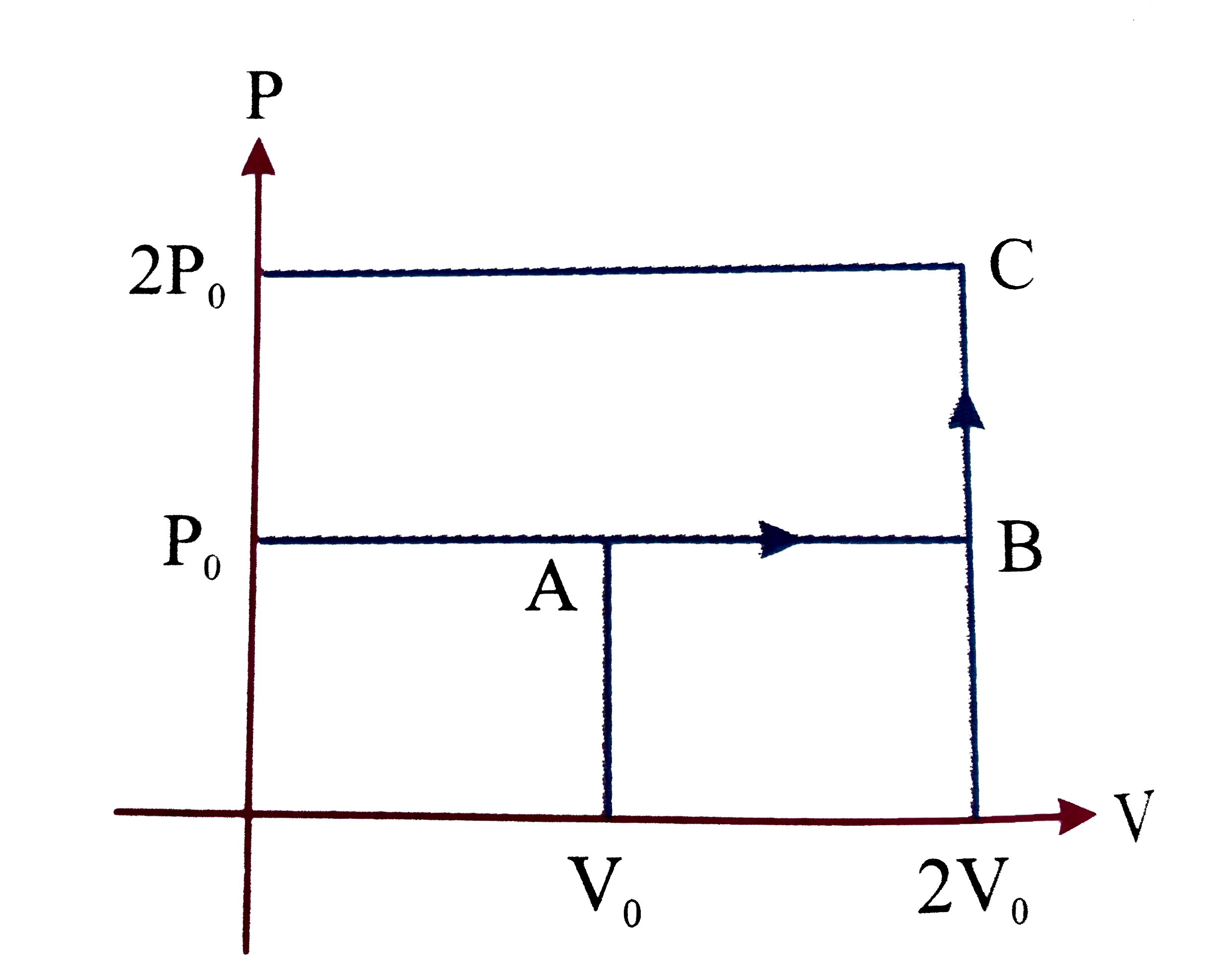
View SolutionTwo cylinders are connected by a fixed diathermic partition `A` and a removable adiabatic partition `B` is placed adjacent to `A` as shown in the figure. Inititally n moles of an ideal monoatomic gas in present in both the cylinders an normal atmospheric pressure `p_(0)` . Both the gases occupy same volume `V_(0)` , initially.
Now the piston of the left cylinder is compressed in adiabatic manner so that volume of the lift portion becomes `(V_(0))/(2)` and then the left piston clamped. Again the adiabatic slider `B` is removed so equilibrium. Assume all other surfaces except `A` to be adiabatic. For this situation, mark out the correct statement (s).

View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature `T_1`, pressure `P_1` and volume `V_1`and the spring is in its relaxed state. The gas is then heated very slowly to temperature `T_2`,pressure `P_2`and volume `V_2`. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)

View SolutionThe molar specific heat of a gas is defined as `C=(Dq)/(ndT)` Where `dQ`=heat absorbed
`n` = mole number `dT` = change in temperature
`A` gas with adiabatic exponent `'gamma'` is expanded accrding to the law `p=alphaV` . The initial volume is `V_(0)` . The final volume is `eta V_(0)`. (`etagt1`). The molar heat capacity of the gas in the process is
View Solution
Exercise questions and complete solutions for chapter THERMODYNAMICS of NARAYANA PHYSICS (HINGLISH) of Class 11