If Pd vs. P(where P denotes pressure in atm and d denotes density in gm/L ) is plotted for He gas (assume ideal ) at a particular temperature. If then the temperature wil be
160 K
320 K
80 K
none of these
The correct Answer is:a
To solve the problem step by step, we will use the relationship between pressure, density, and temperature for an ideal gas.
Step 1: Understand the relationship between density, pressure, and temperature.
For an ideal gas, the density d can be expressed as:
d=PMRT
where:
- P = pressure in atm,
- M = molar mass of the gas (for Helium, M=4g/mol),
- R = ideal gas constant =0.0821L atm/(K mol),
- T = temperature in Kelvin.
Step 2: Multiply both sides by pressure P.
We can rewrite the equation as:
Pd=P2MRT
Step 3: Differentiate Pd with respect to P.
To find d(Pd)dP, we differentiate:
d(Pd)dP=ddP(P2MRT)=2PMRT
Step 4: Substitute the given values.
We know from the problem that:
(d(Pd)dP)P=8.21atm=5
Thus, we can set up the equation:
2PMRT=5
Substituting P=8.21atm and M=4g/mol:
2×8.21×4RT=5
Step 5: Solve for T.
Rearranging the equation gives:
RT=2×8.21×45
Calculating the right side:
RT=65.685=13.136
Now, substituting R=0.0821L atm/(K mol):
T=13.1360.0821≈160K
Final Answer:
The temperature T is approximately 160 K.
---
For an ideal gas, the density d can be expressed as:
d=PMRT
where:
- P = pressure in atm,
- M = molar mass of the gas (for Helium, M=4g/mol),
- R = ideal gas constant =0.0821L atm/(K mol),
- T = temperature in Kelvin.
We can rewrite the equation as:
Pd=P2MRT
To find d(Pd)dP, we differentiate:
d(Pd)dP=ddP(P2MRT)=2PMRT
We know from the problem that:
(d(Pd)dP)P=8.21atm=5
Thus, we can set up the equation:
2PMRT=5
Substituting P=8.21atm and M=4g/mol:
2×8.21×4RT=5
Rearranging the equation gives:
RT=2×8.21×45
Calculating the right side:
RT=65.685=13.136
T=13.1360.0821≈160K
The temperature T is approximately 160 K.
Topper's Solved these Questions
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 1
4 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 2
6 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Subjective problems
15 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems
14 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems
1 Videos
Similar Questions
Knowledge Check
The pressure P1anddensityd1 of a diatomic gas (γ=75) change to P2andd2 during an adiabatic operation .If d2d1=32,thenP2P1is
Aa. 76Bb. 128Cc. 168Dd. 298
Calculate the moles of an ideal gas at pressure 2atm and volume 1L at a temperature of 97.5K
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is the cross-sectional are of the cylinder. at this time, the temperature of the gas has become.

View SolutionAt a constant temperature what is the relation between pressure P density d of an ideal gas ?
View SolutionThe pressure and density of a diatomic gas (γ=75) change adiabatically from (P,d) to P',d'). If d'd=32, then find the value of P'P ?
View SolutionIn the given pressure - temperature (P-T) diagram, the density of an ideal gas at point A and B are ρ0 and 3ρ02respectively, then the value of X is
View SolutionA spherical air bubble is rising from the depth of a lake when pressure is Patm and temperature is TK. The percentage increase in the radius when it comes to the surface of a lake will be (Assume temperature and pressure at the surface to be, respectively, 2TK and P/4.)
View SolutionAnswer the following questions based on the P – T phase diagram of CO2:
(a) CO2 at 1 atm pressure and temperature–60∘C is compressed isothermally. Does it go through a liquid phase ?
(b) What happens when CO2 at 4 atm pressure is cooled from room temperature at constant pressure ?
(c) Describe qualitatively the changes in a given mass of solid CO2 at 10 atm pressure and temperature –65∘C as it is heated up to room temperature at constant pressure.
(d) CO2 is heated to a temperature 70∘C and compressed isothermally. What changes in its properties do you expect to observe ?
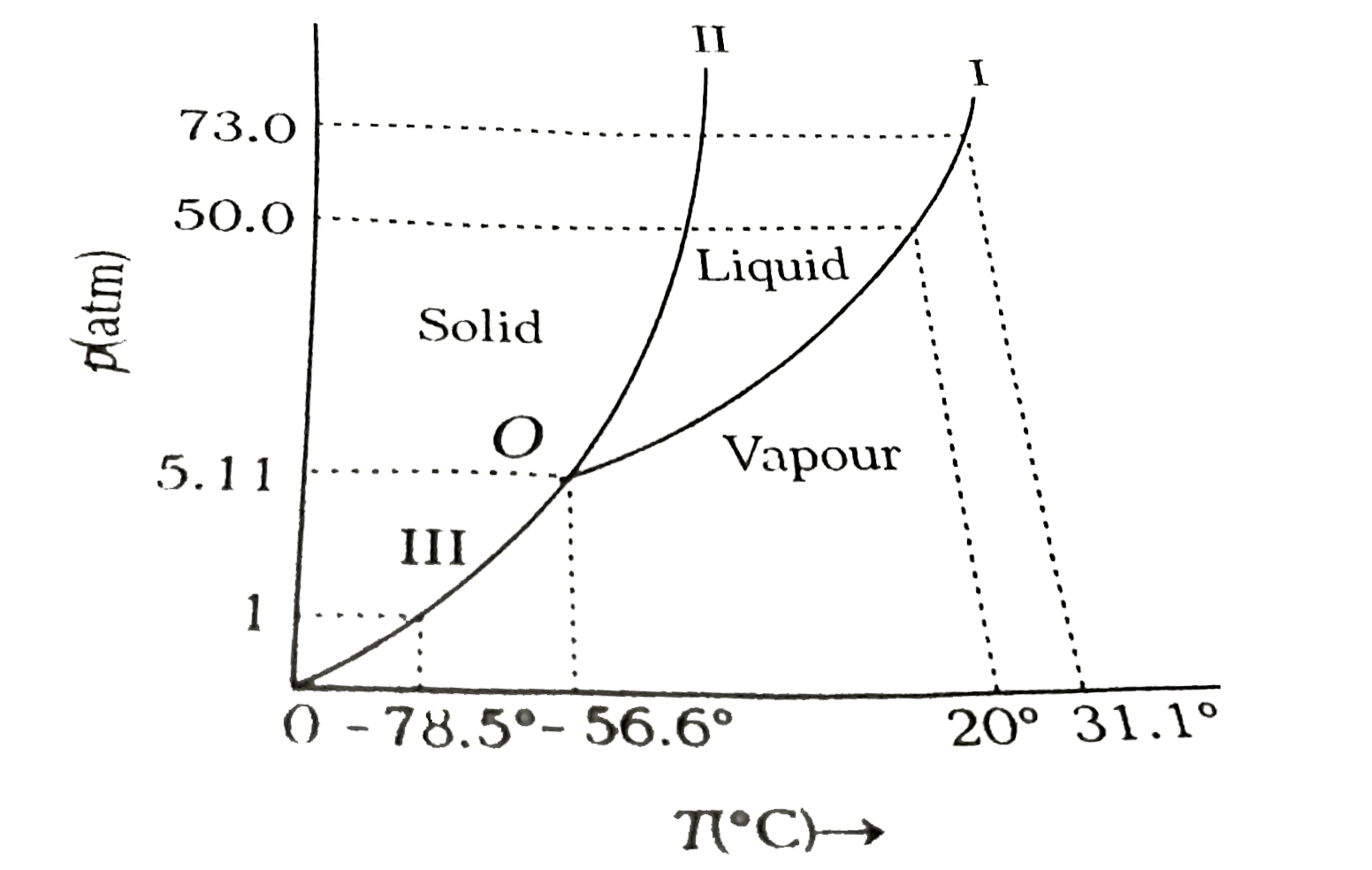
View Solution

