Complete Solutions to All Questions of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| NN GHOSH | All Questions |
| Number Of Questions | 93 |
| Academic Year | 2023-24 |
A train moving at a constant speed of 72 Kmph move eastward for 40 minutes, then in a direction `45^@` east of north for 20 minutes, and finally westwasrd for 50 minutes. What is the average velocity of the train during this run ?
View SolutionA car moving with constant acceleration covers the distance between two points `60m` apart in 6 s. Its speed as it passes the seconds is `15 ms^-1`. (a) What was its speed at the first point ? (b) What is its acceleration ? (c) At what prior distance from the first point was the car at rest ?
View SolutionAn elevator (lift) ascends with an upward acceleration of `1.2ms^-2`. At the instant when its upward speed is `2.4 ms^-1`, a loose bolt drops from the ceiling of the elevator `2.7m` above the floor of the elevator. Calculate (a) the time of flight of the bolt from the ceiling to the floor and (b) the distance it has fallen relaative to the elevator shaft.
View SolutionA car start moving along a line, fisrt with acceleration `a=5 ms^-2` starting from rest then uniformly and finally decelerating at the same rate a, comes to rest. The total time of motion is `pi=25s.` The average velocity during the time is equal to `lt v gt =72 km/hr`. How long does the particle move uniformly ?
View SolutionAt the moment t=0 a particle leaves the origin and moves in the positive direction of the x-axis.Its velocity at any time is `vecv=vecv_0(1-t/tau)` where `v_0=10` cm/s and `tau`=5 s. Find :
(a)the x-coordinates of the particle at the instant 6s, 10s and 20s.
(b)the instant at which it is a distance 10 cm from the origin.
(c )the distance s covered by the particle during the first 4s and 8s.
View SolutionA particle moves in the xy-plane with constant acceleration `a` directed along the negative y-axis. The equation of path of the particle has the form `y= bx - cx^2`, where b and c are positive constants. Find the velocity of the particle at the origin of coordinates.
View SolutionA thief is running away on a straight road in a moving with a speed of `9 ms^(-1)`. A policeman chases him on a motor cycle moving at a speed of `10 ms^(-1)`. If the instantaneous separation of the jeep from the motor cycle is `100 m`, how long will it take for the policeman to catch the thief ?.
View SolutionA man is `l=9m` behind the door of a train when it start moving with acceleration `a=2 m/s^2`. The man runs at full speed. How far does he have to run and after what time does he get into the train ? What is his speed ?
View SolutionTwo bodies are thrown with the same velocity at angles `alpha and 90^@ - alpha` to the horizontal. Calculate the ration of the maximum heights reached by the bodies.
View SolutionA body is thrown at an angle `alpha`to the horizontal with initial velocity `v_0`.Assuming air drag to be negligible , find (i)the time of motion, (ii)maximum height of ascent and the horizontal range, (iii)the angle of projection at which they are equal , (iv)the angle of projection at which the horizontal range is maximum and the angle at which the vertical range is maximum.
View SolutionThe surface of a hill is inclined at an angle `alpha` to the horizontal. A stone is thrown from the summit of the hill at angle `beta` to the velocity `v_0`. How far from the summit will the stone strike the ground ?
View SolutionA fort is at the top of a hill of height h above the sea-level.Prove that the greatest horizontal distance from which a gun in the ship can hit the fort is `2sqrt(k(k-h))` where `sqrt(2gk)` is the muzzle velocity.
View SolutionA body describes the first half of the total distance with velocity `v_1` and the second half and velocity `v_2`.Calculate the average velocity.
View SolutionA particle moves along a horizontal line and its velocity changes with time as shown in the figure.

Calculate (i)initial acceleration, (ii)total distance described . Plot the x-t graph of the motion.
View SolutionA parachutist after bailing out falls freely for 50 metres. Then his parachute opens and he falls with deceleration of `2ms^-2` When he reaches the ground his speed is reduced to only 3 metres per seconds. at what height did he bail out ? For how long was he in air ?
View SolutionA block is released from rest at the top of a frictionless inclined plane, which is 10 m long. It reaches the bottom in 5 seconds.A second block is projected up the plane from the bottom at the instant the first block is released and the two return to the bottom simultaneously.(a)Find the acceleration of each block along the incline.(b)What is the initial velocity of the second block ? (c )How far up the inclined plane does it travel ?
View SolutionTwo cars are moving in the same direction with the same speed with seperetion 40m. In order to overtake, the driver of the second car accelerates and he overtakes the first car in 5 seconds. What is the acceleration produced by the accelerator ?
View SolutionA point traversed half the distance with a velocity `v_0`. The remaining part of the distance was covered with velocity `v_1` for half the time, and with velocity `v_2` for the other half of the time. Find the mean velocity of the point averaged over the whole time of motion.
View SolutionA particle travels with constant speed along a circle of radius `3 m` and completes one revolution in `20 s`. Starting with the lowest point as origin, find (a) the magnitude and direction of the displacement vectors 5 s, 7.5s and 10 s later , (b) the magnitude and direction of the displacement in the 5 s interval from the fifth to the lenth second, (c) average velocity in this interval, (d) the instantaneous velocity at the begining and at the end of the interval.
View SolutionTwo trains, each with a speed of 50 kmph are headed towards each other on the same trake. A bird that can fly at the rate of 100kmph flies off one train when they are 100km apart and heads directly to the other train. On reaching the other train it flies back to the first train and so forth. (a) How many trips can the bird make from one train to the other before they crash ? (b) How is the total distance the bird travels ?
View SolutionA train take 2 minutes to acquire its full speed of 60 kmph from rest and 1 minute to come to rest from the full speed. If somewhere in between two station 1 km of the trake be under repair and the speed limit for this part be 20 kmph, how late will the train be running on account of this repair work, assuming that the train would have been on time otherwise ?
View SolutionA train ball is dropped from the roof of a building. An observer standing in front of a window `1.2m` high notes that the ball takes `1/8 s` to fall from the top to the bottom of the window. The ball continues to fall , makes a completely elastic collision with a horizontal sidewalk and reappears at the bottom of the window 2 s after passing in on the way down. How tall is the building ?
View SolutionA car accelerates from rest at a constant rate ` alpha ` for some time after which it decelerates at a constant rate ` beta` to come to rest. If the total time lapse is ` t` seconds , evauate.
(i) maximum velocity reached , and
(ii) the total distance travelled .
View SolutionTwo bodies start moving in the same straight line at the same instant of time from the same origin. The first body moves with a constant velocity of `40ms^-1`, and the second starts from rest with a constant acceleration of `4ms^-2`.Find the time that elapses before the second catches the first body. Find the also the greatest distance between them prior to it and time at which this occurs.
View SolutionEvery 10 mintues, two cars start simultaneously from two point `A and B` which are 60 km apart. The cars travel towards each other at 60 kmph. Find graphiclly how many cars will pass by a passenger in one of the cars between `A and B`.
View SolutionTwo equal to masses are connected by a light string passing over a fixed frictionless pully. They are set in motion with uniform speed v. The mass going down is momentarily stopped and then released immediately. Calculate the time that will elapse before the string becomes tight again.
View SolutionA man with a constant time of reaction can stop his car within 30m when its speed is 72kmph and within 10m when its speed is 36kmph. What is the distance within which he can stop his car when speeding at 54 km ph ?
View SolutionTwo cars cover the distance between two station in 2 hours. The first car covers the first half of the distance at 20 km ph and the seconds half at 60 km ph and the second car covers the distance with uniform acceleration, starting with a velocity of 10 km ph. At what instant/instants will the two cars have the same velocity ?
View SolutionA point moves in the `x-y` plane according to the equations `x=at, y=at-vt^2` Find : (a) the equation of the trajectory, (b) acceleration as s function of t (c) the instant `t_0` at which the velocity and acceleration are at `pi/4`.
View SolutionThree points are located at the vertices of an equilateral triangle each of whose sides measure a. They all start simultaneously with speed v, each aiming at the next in order. How soon will the points converge ?
View SolutionA truck has to carry a load in the shortest time from one point to another at a distance L from the first. It can only start up or slow down at the same accelertion a. What maximum velocity must the truck attain to satisfy this condition ?
View SolutionThree particles start from the origin at the same time, one with velocity `u_1` along the x-axis, the second with velocity `u_2` along the y-axis . Find the velocity of the third particles, along the x=y line so that the three particles may always lie on the same straight line.
View SolutionA body projected vertically upwards from A, the top of a tower, reaches the ground in `t_1` seconds.If it is projected vertically downwards from A with the same velocity, it reaches the ground in `t_2` seconds.If it falls freely from rest at A, in what time does it reach the ground ?
View SolutionA body projected with the same velocity at two different angles covers the same horizontal distance R. If `t and t'` are two times of flight, prove that `R=1/2 gtt`.
View SolutionThe celling of a long hall is 25m high. What is the maximum horizontal distance that a ball thrown with a speed of `40ms^-1` can cover without hitting the celling of the hall ? At what angle and from where it be thrown ?
View SolutionA cannon a target are `5.0 km` apart on the same horizontal plane. How long will the shell launched with a velocity of `240 ms^-1` take to reach the tanget ? `(g=10ms^-2)`
View SolutionA ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle `alpha` with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time ?
View SolutionA cannon fires two shells successively with velocity `250 m s^(-1)` at angles `60^@` and `45^@` with the horizontal in the same vertical plane one after the other . What should be the interval between the firings so that they may hit the same target simultaneously ?
View SolutionA machine gun is mounted on the top of a tower of height h=100 m. At what angle should the gun be inclined to cover a maximum range of firing on the ground below ?The muzzle speed of the bullet is `u=150 m s^(-1)` and `g=10 m s^(-2)` .
View SolutionA cannon fires its projectile with such an initial velocity and angle of projection that its range is R and the maximum height to which the projectile rises is H. Find the maximum range that can be obtained with the same initial velocity.
View SolutionAn airplane is moving with velocity `v_0` horizontally at a height h. If a projectile is fired at the instant when the plane is overhead, What must be the angle of projection amd minimum velocity of projection in order that it may hit the airplane ?
View SolutionA parrticle projected with velocity u strikes at right angles a plane through the point of projection inclined at angle `beta` to the horizon. Show that the height of the point struck above the horizontal plane through the point of projection is `(2u^2)/g . (sin^2 beta)/(1+3 sin^2 beta)` and that the time of flight up to that instant is `t=(2u)/(g sqrt(1+3 sin^2 beta))`.
View SolutionA train moving at a constant speed of 72 kmph moves eastward for 40 minutes, then in a direction `45^@` east to north for 20 minutes, and finally westward for 50 minutes.What is the average velocity of the train during the run ?
View SolutionA car moving with constant acceleration covers the distance between two points 60 m apart in 6s. Its speed as it passes the second point is `15 ms^(-1)`.(a)What was its speed at the first point ? (b)What is its acceleration ? (c )At what prior distance from the first point was the car at rest ?
View SolutionAn elevator (lift) ascends with an upward acceleration of 1.2 `ms^(-2)`.At the instant when its upward speed is 2.4 `ms^(-1)`, a loose bolt drops from the ceiling of the elevator 2.7 m above the floor of the elevator . Calculate (a) the time of flight of the bolt from the ceiling to the floor and (b)the distance it has fallen relative to the elevator shaft.
View SolutionA car starts moving along a line, first with acceleration a=5 `ms^(-2)` starting from rest then uniformly and finally decelerating at the same rate a, comes to rest.The total time of motion is `tau=25 s`. The average velocity during the time is equal to lt v gt =72 km/hr.How long does the partial move uniformly ?
View SolutionAt the moment t=0 a particle leaves the origin and moves in the positive direction of the x-axis.Its velocity at any time is `vecv=vecv_0(1-t/tau)` where `v_0=10` cm/s and `tau`=5 s. Find :
(a)the x-coordinates of the particle at the instant 6s, 10s and 20s.
(b)the instant at which it is a distance 10 cm from the origin.
(c )the distance s covered by the particle during the first 4s and 8s.
View SolutionDraw graphs of the speeds and path lengths as functions of time if the graph of acceleration is as shown below . The initial speed is zero .
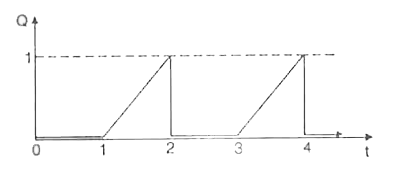
View SolutionA particle moves in the x-y plane with constant acceleration `alpha` directed along the negative direction of the y-axis.the equation of the trajectory of the particle is y=ax-`bx^2`, where a and b are constants. Find the velocity of the particle when it passes through the origin.
View SolutionA man is l=9 m behind the door of a train when it starts moving with acceleration a=`2 m//s^2`.The man runs at full speed. How far does he have to run and after what time does he get into the train ? What is his full speed ?
View SolutionTwo bodies are thrown with the same velocity at angles `alpha` and `90^@-alpha` to the horizontal.Calculate the ratio of the maximum heights reached by the bodies.
View SolutionA body is thrown at an angle `alpha`to the horizontal with initial velocity `v_0`.Assuming air drag to be negligible , find (i)the time of motion, (ii)maximum height of ascent and the horizontal range, (iii)the angle of projection at which they are equal , (iv)the angle of projection at which the horizontal range is maximum and the angle at which the vertical range is maximum.
View SolutionThe surface of a hill is inclined at an angle `alpha` to the horizontal .A stone is thrown from the summit of the hill at an angle `beta` to the vertical with velocity `v_0`.How far from the summit will the stone strike the ground ?
View SolutionA fort is at the top of a hill of height h above the sea-level.Prove that the greatest horizontal distance from which a gun in the ship can hit the fort is `2sqrt(k(k-h))` where `sqrt(2gk)` is the muzzle velocity.
View SolutionIf a body travels half the distance with velocity `v_(1)` and next half with velocity `v_(2),` then which one of the following will be the average velocity of the body?
View SolutionA particle moves along a horizontal line and its velocity changes with time as shown in the figure.

Calculate (i)initial acceleration, (ii)total distance described . Plot the x-t graph of the motion.
View SolutionA parachutist after bailing out falls freely for 50 metres.Then his parachute opens and he falls with deceleration of `2 ms^(-2)` When he reaches the ground his speed is reduced to only 3 metres per second.At what height did he bail out ? For how long was he in air ?
View SolutionA block is released from rest at the top of a frictionless inclined plane, which is 10 m long. It reaches the bottom in 5 seconds.A second block is projected up the plane from the bottom at the instant the first block is released and the two return to the bottom simultaneously.(a)Find the acceleration of each block along the incline.(b)What is the initial velocity of the second block ? (c )How far up the inclined plane does it travel ?
View SolutionA plot of velocity versus time for a body in rectilinear motion is as shown in the figure.indicate whether acceleration is positive, negative , zero , variable or constant in the region OA, AB, BC and CD.Calculate the distance described up to the point C.What is the displacement up to point C ?
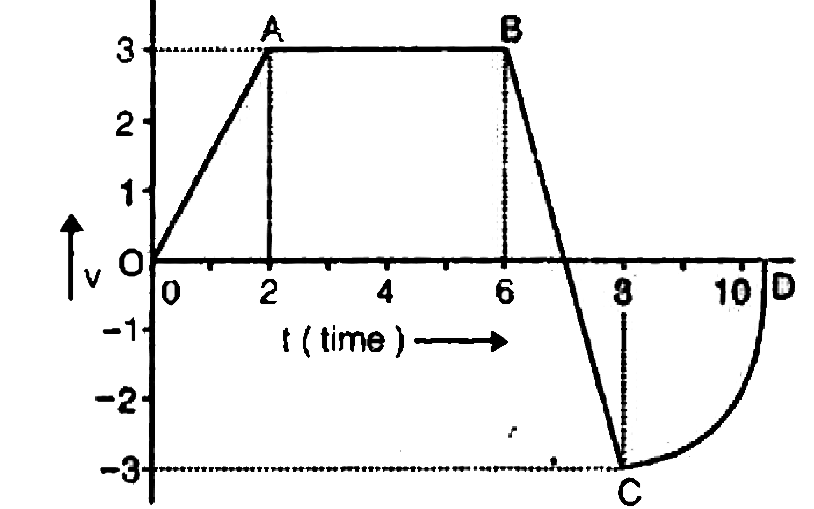
View SolutionIf the same plot is of displacement (x) versus time (t), indicate whether the body is at rest or in motion and whether it has uniform velocity or variable velocity in the rigions OA, AB, BC and CD.Find the distance described in 8 s.What is the displacement of the body in 8 s ?
View SolutionTwo cars are moving in the same direction with the same speed with separation 40 m.In order to overtake, the driver of the second car accelerates and he overtakes the first car in 5 seconds.What is the acceleration produced by the accelerator ?
View SolutionA piece of stone is allowed to fall from a balloon floating in air. It goes down past a tower 30 m in height in the last quarter of the last second of its flight.Find the height of the stone at the instant when it was dropped and its velocity as it reaches the ground. `(g=9.8 ms^(-2))`
View SolutionA body travels half of its total path in the last second of its fall from rest.Find the height from which it falls and the time of flight.
View SolutionA point traversed half of the total distance covered by its with velocity `v_0`.The remaining part of the distance was covered with velocity `v_1` for half of the remaining time, and with velocity `v_2` for the other half of the remaining time.Find the mean velocity of the point over the whole time of motion.
View SolutionThe driver of a train moving at a speed ` v_(1)` sights another train at a disane ` d`, ahead of him moving in the same direction with a slower speed ` v_(2)`. He applies the brakes and gives a constant teradation ` a` to his train. Show that here will be no collision if ` d gt (v_(1) -v_(2))^(2) //2 a`.
View SolutionA particle travels with constant speed along a circle of radius `3 m` and completes one revolution in `20 s`. Starting with the lowest point as origin, find (a) the magnitude and direction of the displacement vectors 5 s, 7.5s and 10 s later , (b) the magnitude and direction of the displacement in the 5 s interval from the fifth to the lenth second, (c) average velocity in this interval, (d) the instantaneous velocity at the begining and at the end of the interval.
View SolutionTwo trains, each with a speed of 50 kmph are headed towards each other on the same trake. A bird that can fly at the rate of 100kmph flies off one train when they are 100km apart and heads directly to the other train. On reaching the other train it flies back to the first train and so forth. (a) How many trips can the bird make from one train to the other before they crash ? (b) How is the total distance the bird travels ?
View SolutionA train take 2 minutes to acquire its full speed of 60 kmph from rest and 1 minute to come to rest from the full speed. If somewhere in between two station 1 km of the trake be under repair and the speed limit for this part be 20 kmph, how late will the train be running on account of this repair work, assuming that the train would have been on time otherwise ?
View SolutionA steel ball is dropped from the roof of a building.An observer standing in front of a window 1.2 m high notes that the ball takes `1/8` s to fall from the top to the bottom of the window.The ball continues to fall, makes a completely elastic collision with a horizontal sidewalk and reappears at the bottom of the window 2 s after passing it on the way down. How tall is the building ?
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta` and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View SolutionA body begins to move with an initial velocity of `2 m s^(-1)` and continues to move at a constant acceleration a.Ten seconds later a second body begins to move from the same point with an initial velocity of `12 m s^(-1)` in the same direction with the same acceleration.What is the maximum acceleration at which it would be possible for the second body to overtake the first ?
View SolutionEvery 10 mintues, two cars start simultaneously from two point `A and B` which are 60 km apart. The cars travel towards each other at 60 kmph. Find graphiclly how many cars will pass by a passenger in one of the cars between `A and B`.
View SolutionTwo equal to masses are connected by a light string passing over a fixed frictionless pully. They are set in motion with uniform speed v. The mass going down is momentarily stopped and then released immediately. Calculate the time that will elapse before the string becomes tight again.
View SolutionA man with a constant time of reaction can stop his car within 30 m when its speed is 72 kmph and within 10 m when its speed is 36 kmph.What is the distance within which he can stop his car when speeding at 54 kmph ?
View SolutionTwo cars cover the distance between two stations in 2 hours. The first car covers the first half of the distance at 20 kmph and the second half at 60 kmph and the second car covers the distance with uniform acceleration, starting with a velocity of 10 kmph.At what instant/instants will the two cars have the same velocity ?
View SolutionA point moves in the x-y plane according to the equations x=at, y=at-`bt^2`.Find (a)the equation of the trajectory, (b)acceleration as a function of t, (c )the instant `t_0` at which the velocity and acceleration are at `pi//4` .
View SolutionThree points are located at the vertices of an equilateral triangle each of whose sides measure a. They all start simultaneously with speed v, each aiming at the next in order. How soon will the points converge ?
View SolutionA truck has to carry a load in the shortest time from one point to another at a distance L from the first.It can only start up or slow down at the same acceleration a. What maximum velocity must the truck attain to satisfy this condition ?
View SolutionThree particles start from the origin at the same time, one with velocity `u_1` along the x-axis, the second with velocity `u_2` along the y-axis . Find the velocity of the third particles, along the x=y line so that the three particles may always lie on the same straight line.
View SolutionA body projected vertically upwards from A, the top of a tower, reaches the ground in `t_1` seconds.If it is projected vertically downwards from A with the same velocity, it reaches the ground in `t_2` seconds.If it falls freely from rest at A, in what time does it reach the ground ?
View SolutionA body projected with the same velocity at two different angles covers the same horizontal distance R.If t and t' are the two times of flight, prove that `R=1/2 gtt'`
View SolutionThe ceiling of a long hall is 25 m high.What is the maximum horizontal distance that a ball thrown with a speed of `40 ms^(-1)` can cover without hitting the ceiling of the hall ? At what angle and from must it be thrown ?
View SolutionA cannon and a target are 5.0 km apart on the same horizontal plane. How long will the shell, launched with a velocity of `240 m s^(-1)`, take to reach the target ? `(g=10 ms^(-2))`
View SolutionA ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle `alpha` with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane . At what distance from the impact point will the ball rebound for the second time ?
View SolutionA cannon fires two shells successively with velocity `250 m s^(-1)` at angles `60^@` and `45^@` with the horizontal in the same vertical plane one after the other . What should be the interval between the firings so that they may hit the same target simultaneously ?
View SolutionA machine gun is mounted on the top of a tower of height h=100 m. At what angle should the gun be inclined to cover a maximum range of firing on the ground below ?The muzzle speed of the bullet is `u=150 m s^(-1)` and `g=10 m s^(-2)` .
View SolutionA cannon fires its projectile with such an initial velocity and angle of projection that its range is R and the maximum height to which the projectile rises is H.Find the maximum range that can be obtained with the same initial velocity.
View SolutionAn airplane is moving with velocity `v_0` horizontally at a height h. If a projectile is fired at the instant when the plane is overhead, what must be the angle of projection and minimum velocity of projection in order that it may hit the airplane ?
View SolutionA parrticle projected with velocity u strikes at right angles a plane through the point of projection inclined at angle `beta` to the horizon. Show that the height of the point struck above the horizontal plane through the point of projection is `(2u^2)/g . (sin^2 beta)/(1+3 sin^2 beta)` and that the time of flight up to that instant is `t=(2u)/(g sqrt(1+3 sin^2 beta))`.
View SolutionA particle is projected with a velocity u from a point at ground level. Show that it cannot clear a wall of height h at a distance x from the point of projection if `u^2 lt g(h+sqrt(h^2+x^2))`.
View SolutionA projectile is required to hit a target whose coordinates relative to the horizontal and vertical axes through the point of projectile are (a,b) . If the muzzle velocity is `sqrt(2ga)`, show that it is impossible to hit the target if `b ge3/4a`.
View SolutionTwo particles are projected at the same instant from the same point of inclinations `alpha` and `beta` to the horizontal.if they simultaneously hit the top and the bottom of a vertical pole subtending an angle `gamma` at the point of projection, show that `tan -alpha tan beta=tan gamma`.
View SolutionA target situated on a hill can be seen from the foot at angle `alpha` above the horizontal .The distance of the target along the horizonal is R. if a shell is fired from the foot at an angle `beta` with the horizontal, find the velocity required for it to strike the target.
View Solution
All Questions questions and complete solutions for chapter KINEMATICS of BHARATI BHAWAN PHYSICS (HINGLISH) of Class 11