Complete Solutions to Advanced Level Problems of chapter CALORIMETRY AND THERMAL EXPANSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY AND THERMAL EXPANSION |
| RESONANCE | Advanced Level Problems |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
A thermally insulated, closed copper vessel contains water at `15^@C`. When the vessel is shaken vigorously for 15 minuts, the temperature rises to `17^@C`. The mass of the vessel is 100 g and that of the water is 200 g. The specific heat capacities of copper and water are `420(J)/(kg-K)` and `4200(J)/(kg-K)` resprectively. Neglect any thermal expansion.
(a) How much heat is transferred to the liquid vessel system?
(b) How much work has been doen on this system?
(c ) How much is the increase in internal energy of the system?
View SolutionThe time represented by the clock hands of a pendulum clock depends on the number of oscillations performed by pendulum. Every time it reaches to its exterme position the second hand of the clock advances by one second that means second hand moves by two second when one oscillation is completed.
(a) How many number of oscillations completed by pendulum of clock in `15` minutes at calibrated temperature `20^(@)C`
(b) How many number of oscillations are completed by a pendulum of clock in `15` minutes at temperature of `40^(@)C if alpha = 2 xx 10^(-5)//"^(@)C`
(c ) What time is represented by the pendulum clock at `40^(@)C` after `15` minutes if the initial time shown by the clock is `12:00` pm?
(d) If the clock gains two seconds in `15` minutes in correct clock then find-(i) Number of extra oscillations (ii) New time period (iii) change in temperature.
View SolutionConsider a cylindrical container of cross-section area A length h and having coefficient of linear expansion `alpha_(c)`. The container is filled by liquid of real expansion coefficient `gamma_(L)` up to height `h_(1)`. When temperature of the system is increased by `Deltatheta` then
(a). Find out the height, area and volume of cylindrical container and new volume of liquid.
(b). Find the height of liquid level when expansion of container is neglected.
(c). Find the relation between `gamma_(L)` and `alpha_(c)` for which volume of container above the liquid level
(i) increases
(ii). decreases
(iii). remains constant.
(d). On the surface of a cylindrical container a scale is attached for the measurement of level of liquid of liquid filled inside it. If we increase the temperature of the temperature of the system by `Deltatheta`, then
(i). Find height of liquid level as shown by the scale on the vessel. Neglect expansion of liquid.
(ii). Find the height of liquid level as shown by the scale on the vessel. Neglect expansion of container.

View SolutionOne gram of water `(1 cm^3)` becomes `1671 cm^3` of steam when boiled at a constant pressure of 1 atm `(1.013xx10^5Pa)`. The heat of vaporization at this pressure is `L_v=2.256xx10^6J//kg`. Compute (a) the work done by the water when it vaporizes and (b) its increase in internal energy.
View SolutionA metal piece weighing `15 g` is heated to `100^(@)C` and then immersed in a mixture of ice and water at the thermal equilibrium. The volume of the mixture is found to be reduced by `0.15 cm^(3)` with the temperature of mixture remaining constant. Find the specific heat of the metal. Given specific gravity of ice `= 0.92`, specific gravity of water at `0^(@)C = 1.0`, latent heat of fusion of ice `= 80 cal-g^(-1)`.
View Solution(a) The brass scale of a barometer gives correct reading at `0^(@)C` . Coefficient of linear expansion of brass is `2.0xx10^(-5)//^(@)C` . The barometer reads `75cm` at `27^(@)C` . What is the atmospheric pressure at `27^(@)C` ?
(b) A barometer reads `75.0cm` on a steel scale. The room temperature is `30^(@)C` . The scale is correctly graduated for `0^(@)C ` . The coefficient of linear expansion of steel is `alpha=1.2xx10^(-5)//^(@)C` and the coefficient of volume expansion of mercury is `gamma=1.8xx10^(-4)//^(@)C` . Find the correct atmospheric pressure.
View SolutionA clock with an iron pendulum keeps correct time at `20^(@)C`. How much time will it lose or gain in a day if the temperature changes to `40^(@)C`. Thermal coefficient of liner expansion `alpha = 0.000012 per^(@)C`.
View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length `l_1`, coefficient of linear expansion `alpha_1` and Young's modulus `Y_1`. The correcsponding quantities for second rod are `l_2,alpha_2` and `Y_2`. The temperature of both the rods is now raised by `t^@C`.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At `25^(@)C`, the composite rod is `1 m` long and the copper rod is `30 cm` long. At `125^(@)C` the length of the composite rod increases by `1.91 mm`. When the composite rod is prevented from expanding by holding it between two rigid walls, it is found that the constituent rods have remained unchanged in length inspite of rise of temperature. Find young's modulus and the coefficient of linear expansion of the second rod (Y of copper `=1.3xx10^(10) N//m^(2)` and `a` of copper `=17xx10^(-6)//K`).
View SolutionA piece of metal weighs 46 g in air and 30 g in liquid of density `1.24 xx 10^3 kg m^(-3)` kept at `27^0C`. When the temperature of the liquid is raised to `42^0C`, the metal piece weights 30.5 g . The density of the liquid at `42^0 C` is `1.20 xx 10^3 kg m^(-3)`. Calculate the coefficient of linear expansion of the metal.
View SolutionTwo steel rods and an aluminium rod of equal length `l_0` and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at `0^@ C`. Find the length of the system when the temperature is raised to `theta`. Coefficient of linear expansion of aluminium and steel are `alpha_(a)` and `alpha_(s)` respectively. Young's modulus of aluminium is `Y_(a)` and of steel is `Y_(s)`.
View SolutionConsider a metal scale of length `30cm` and an object. The scale is calibrated for temp `20^(@)C`.
(a) What is the actual length of division which is shown as `1cm` by scale at `40^(@)C`. Given `alpha_(s) = 2 xx 10^(-5)//"^(@)C`.
(b) What will be the reading of scale at `40^(@)C` if the actual length of objects is `10cm`.
(c ) What will be the actual length of object at `40^(@)C` if is measured length is `10cm`.
(d) What is `%` error in measurement for part (b) and (c).
(e) If the linear expansion coefficient of object is `alpha_(0) = 4 xx 10^(-5)` and neglecting the expansion of scale, then answers of (b) and (c) parts.
(f) If `alpha_(0) = 4 xx 10^(-5)` and `alpha_(s) =2xx 10^(-5)` then find answers of (b) and (c) part.
View SolutionThe apparatus shown in the figure consists of four glass columns connected by horizontal section. The height of two central column B and C are 49 cm each. The two outer columns A and D are open to the temperature. A and C are maintained at a temperature of `95^@C` while the columns B and D are maintained at `5^@C`. The height of the liquid in A and D measured from the base the are 52.8 cm and 51cm respectively. Determine the coefficient of thermal expansion of the liquid
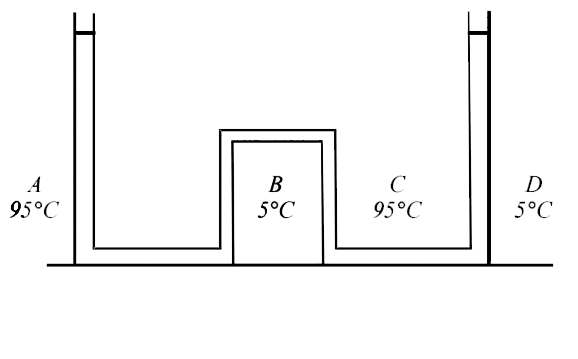
View Solution
Advanced Level Problems questions and complete solutions for chapter CALORIMETRY AND THERMAL EXPANSION of RESONANCE ENGLISH of Class 11