Complete Solutions to Exercise of chapter CALORIMETRY AND THERMAL EXPANSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY AND THERMAL EXPANSION |
| RESONANCE | Exercise |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
A piece of ice falls from a height `h` so that it melts completely. Only one-quarter of the heat produced is absobed by the ice and all energy of ice gets converted into heat during its fall. The value of `h` is
[Latent heat of ice is `3.4 xx 10^(5) J//kg` and `g = 10 N//kg`]
View SolutionA copper cube of mass `200g` slides down an a rough inclined plane of inclination `37^(@)` at a constant speed. Assume that any loss in mechanical energy goes into the copper block as thermal energy .Find the increase in the temperature of the block as it slides down through `60cm`. Specific heat capacity of copper `= 420J kg^(-1) K^(-1)`
View SolutionA paddle wheel is connected with a block of mass `10kg` as shown in figure. The wheel is completely immersed in liquid of heat capacity `400 J//K` . The container is adiabatic. For the time interval in which block goes down `1m` slowly calculate
(a) Work done on the liquid
(b) Heat supplied to the liquid
(c ) Rise in the temperature of the liquid Neglect the heat capacity of the container and the paddle. `(g = 10 m//s^(2))`

View Solution300 grams of water at `25^@ C` is added to 100 grams of ice at `0^@ C.` The final temperature of the mixture is _____ `^@C`
View SolutionThe temperature of a metal ball is raised. Arrange the percentage change in volume, surface area and raidus in ascending order.
View SolutionA brass disc fits snugly in a hole in a steel plate. Should you heat or cool this system to losen the disc from the hole ? given that `alpha _b gt alpha _Fe`.
View SolutionTemperature of plate is increased by `Delta theta` then find new

View SolutionWe have a hollow sphere and a solid sphere equal radii and of the same material. They are heated to raise their temperature be equal amounts. How will the cange in their volumes, due to volume expansions, be related? Consider two cases (i) hollow sphere is filled with air, (ii) there is vaccum inside the hollow sphere.
View SolutionWhat should be the sum of lengths of an aluminium and steel rod at `0^(@)C` is, so that all the temperature their difference in length is `0.25m`. (Take coefficient of linear expansion for aluminium and steel at `0^(@)C` as `22 xx 10^(-6)//.^(@)C` and `11 xx 10^(-5)//.^(@)C` respectively.)
View SolutionA steel tape is correctly calibrated at `20^(@)C` and is used to measure the length of a table at `30^(@)C`. Find the percentage error in the measurement of length. `[alpha_(steel) = 11 xx 10^(-5)//.^(@)C]`
View SolutionThe figure shows three temperature scales with the freezing and boiling points of water indicated.
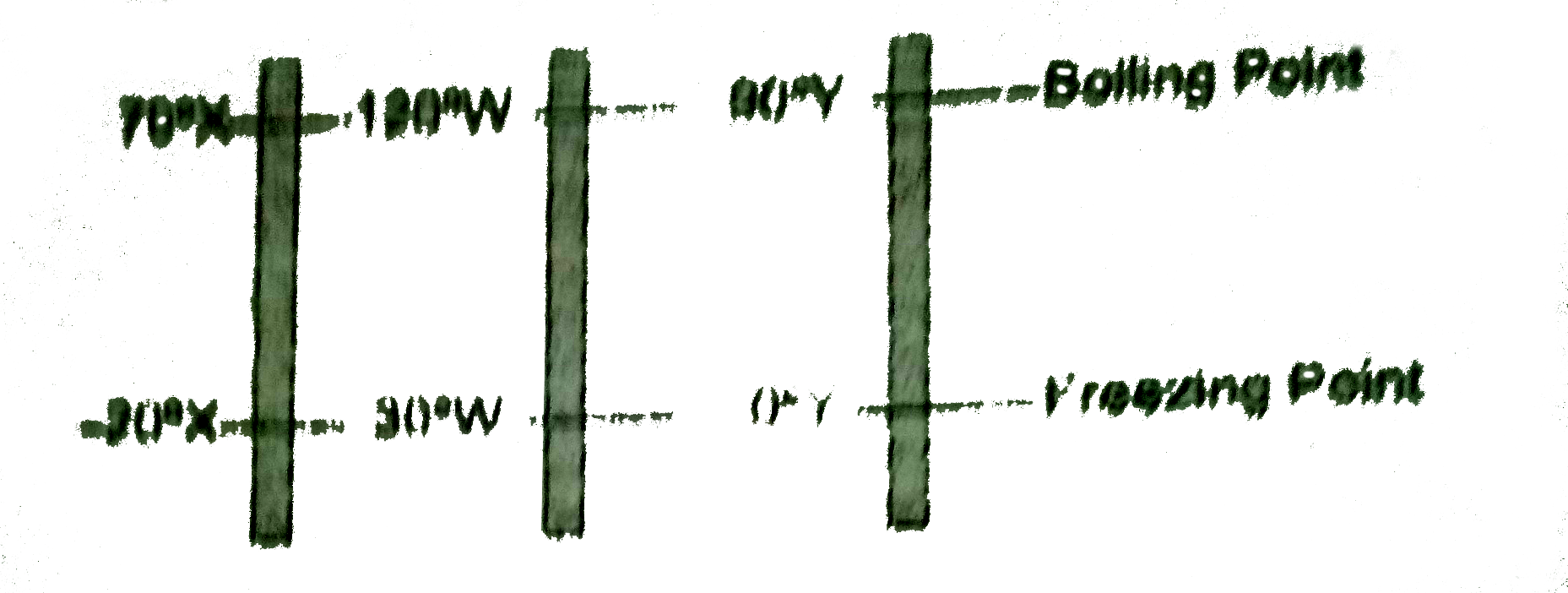
(a) Rank the size of a degree on these scales, greatest first.
(b) Rank the following temperatures, highest first `:50^(@)X,50^(@)W` and `50^(@)Y`.
View SolutionAt what temperature the Fahrenheit and Celsius scales of temperature give the same reading ?.
View SolutionA small quantity mass m, of water at a temperature `theta ("in " ^(@)C)` is poured on to a larger mass M of ice which is at its melting point. If c is the specific heat capacity of water and L the specific heat capacity of water and L the specific latent heat of fusion of ice, then the mass of ice melted is give by
View SolutionA thermally isolated vessel contains `100`g of water at `0^(@)C` when air above the water is pumped out, some of the water freezes and some evaporates at `0^(@)C` itself. Calculate the mass at `0^(@)C=2.10xx10^(6) j//kg` and latent heat of fusion of ice `=3.36xx10^(5) j//kg`.
View Solution`20 gm` ice at `-10^(@)C` is mixed with `m gm` steam at `100^(@)C`. The minimum value of `m` so that finally all ice and steam converts into water is: `("Use " s_("ice") = 0.5 "cal gm"^(@)C, S_("water") = 1 cal//gm^(@)C, L`) (melting) `= 80 cal// gm` and `L ("vaporization") = 540 cal//gm`)
View Solution`2kg` ice at `-20"^(@)C` is mixed with `5kg` water at `20"^(@)C`. Then final amount of water in the mixture will be: [specific heat of ice `=0.5 cal//gm "^(@)C`, Specific heat of water `=1 cal//gm"^(@)C`, Latent heat of fusion of ice `= 80 cal//gm]`
View SolutionTwo large holes are cur in a metal sheet. If this is heated, distance AB and BC, (as shown)

View SolutionA steel scale is to be prepared such that the millimeter intervals are to be accurate within `6 xx10^(-5)mm`. The maximum temperature variation form the temperature of calibration during the reading of the millimeter marks is `(alpha = 12 xx 10^(-6)//"^(@)C)`
View SolutionExpansion during heating
View SolutionIf a bimetallic strip is heated it will
View SolutionTwo rods, one of aluminium and other made of steel, having initial lengths `l_(1) and l_(2)` are connected together to form a single rod of length `(l_(1)+l_(2))`. The coefficient of linear expansions for aluminium and steel are `alpha_(a)` and `alpha_(s)` respectively. If length of each rod increases by same amount when their tempertures are raised by `t^(@)C`, then find the ratio `l_(1) (l_(1)+l_(2))`.
View SolutionA liquid with coefficient of volume expansion `gamma` is filled in a container of a material having coefficient of linear expansion `alpha` . If the liquid overflows on heating, then
View Solutionif two temperatures differ by `25` degree on celsius scale, the difference of temperature on Fahrenheit scale is
View SolutionA substance of mass M kg requires a power input of P wants to remain in the molten state at its melting point. When the power source is turned off, the sample completely solidifies in time t seconds. The latent heat of fusion of the substance is …….
View SolutionSteam at `100^@C` is passed into 1.1 kg of water contained in a calorimeter of water equivalent 0.02 kg at `15^@C`till the temperature of the calorimeter and its contents rises to `80^@C` . The mass of the steam condensed in kilogram is
View SolutionIf I is the moment of inertia of a solid body having `alpha`-coefficient of linear expansion then the change in I corresponding to a small change in temperature `DeltaT` is
View SolutionTwo rods having lengths `l_(1)` and `l_(2)`, made of material with linear expansion coefficients `alpha_(1)` and `alpha_(2)` were soldered together. The equivalent coefficeints linear expansion for the composite rod is

View SolutionShow that the volume thermal expansion coefficient for an ideal gas at constant pressure is `(1)/(T)`.
View SolutionA metal ball immersed in water weighs `w_(1)` at `5^(@)C` and `w_(2) at 50^(@)C`. The coefficient of cubical expansion of metal is less than that of water. Then
View SolutionA piece of metal floats on mercury. The coefficient of volume expansion of metal and mercury are `gamma_1 and gamma_2`, respectively. if the temperature of both mercury and metal are increased by an amount `Delta T`, by what factor does the fraction of the volume of the metal submerged in mercury changes ?
View SolutionTwo vertical glass tibes filled with a liquid are connected at their lower ends by a horizontal capillary tube. One tube is surrounded by a bath containing ice and water at `0^(@)C` and the other by hot water a `t^(@)C`. The difference in the height of the liquid in the two columns is `Deltah`, and the height of the colume at `0^(@)C` is `h_(0)`. coefficient of volume expansion of the liquid is.

View SolutionThe gas thermometers are more sensitive than liquid thermometers because gases
View SolutionSTATEMENT-1: When water is heated by a burner in metallic container its level first decreases then increases.
STATEMENT-2: Thermal conductivity of metal is very compared to water.
View SolutionA pitcher contains `200kg` of water `0.5 gm` of water comes out on the surface of the pitcher every second through the pores and gets evaporated taking energy form the remaining water. Calculate the approximate time (in min) in which temperature of the water decreases by `5^(@)C`. Neglect backward heat transfer form the atmosphere to th water. (Write the answer to the nearest interger)
Specific heat capacity of water `= 4200 J//Kg^(@)C`
Latent heat of vaporization of water `2.27 xx10^(6)J//Kg`

View SolutionHow long does a `59 kw` water heater take to raise the temperature of `150L` of water from `21^(@)C` to `38^(@)C` (in min)
View SolutionThe specific heat of a substance varies with temperature according to `c =0.2 +0.16 T + 0.024 T^(2)` with `T` in `"^(@)c` and `c` is `cal//gk`. Find the energy (in cal) required to raise the temp of `2g` substance from `0^(@)to 5^(@)C`
View Solution`50g` of ice at `0^(@)C` is mixed with `200g` of water at `0^(@)C.6` kcal heat is given to system [Ice +water]. Find the temperature (in `.^(@)C`) of the system.
View SolutionEarth receives `1400 W//m^2` of solar power. If all the solar energy falling on a lens of area `0.2m^2` is focused on to a block of ice of mass 280 grams, the time taken to melt the ice will be….. Minutes. (`Latent heat of fusion of ice`=`3.3xx10^5J//kg`.)
View SolutionA 50gram lead bullet, specific heat 0.02 is initially at `30^(@)` C. It is fired vertically upwards with a speed of `840 m// s` . On returning to the starting level, it strikes a cake of ice at `0^(@)C`. How much ice is melted ? Assume that all energy is spent in melting ice only. Take latent heat of ice `= 80 cal. //` gram.
View SolutionThe temperature of 100g of water is to be raised from `24^@C` to `90^@C` by adding steam to it. Calculate the mass of the steam required for this purpose.
View SolutionAn electrically heated coil is immersed in a calorimeter containing 360 g of water at `10^@C`. The coil consumes energy at the rate of 90 W. The water equivalent of calorimeter and coil is 40 g. The temperature of water after 10 min is
View Solution
As a result of temp rise of `32^(@)C`, a bar with a crack at its centre buckless upward. If the fixed distance `l_(0)` is `4m`, and coefficeient of linear expansion of bar in `25 xx 10^(-5)'^(@)C^(-1)`. Find the rise `x` (in cm) of the centre.
View Solution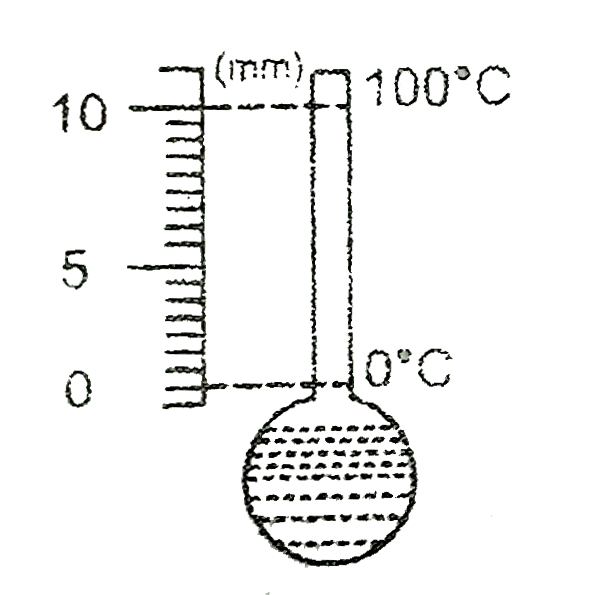
Level of a certain liquid at `0^(@)C` and `100^(@)C` are `0` and `10 mm` on a given fixed scale (as shown in fig.) coefficient of volume expansion this liquid varies with temperature as `gamma = gamma_(0) (1+(T)/(100))` (where `T` in `.^(@)C)` Find the level (in mm) of liquid at `48^(@)C`
View SolutionA simple seconds pendulum is constructed out of a very thin string of thermal coefficient of linear expansion `alpha = 20 xx 10^(-4)//^(@)C` and a heavy particle attached to one end. The free end of the string is suspended from the ceiling of an elevator at rest. the pendulum keeps correct time at `0^(@)C`. when the temperature rises to `50^(@)C`, the elevator operator of mass `60 kg` being a student of Physics accelerates the elevator vertically, to have the pendulum correct time. the apparent weight of the operator when the pendulum keeps correct time at `50^(@)C` is `("Take " g = 10m//s^(2)`)
View SolutionA steel rod of length `25cm` has a cross-sectional area of `0.8cm^(2)` . The force required to stretch this rod by the same amount as the expansion produced by heating it through `10^(@)C` is `(alpha_(steel)=10^(-5)//^(@)C` and `Y_(steel)=2xx10^(10)N//m^(2))`
View SolutionA 1-L flask contains some mercury. It is found that at different temperature, the volume of air inside the flask remains the same. What is the volume of mercury in the flask, given that the coefficient of linear expansion of glass`=9xx10^(-6)//^(@)C` and the coefficient of volume expansion of `Hg=1.8xx10^(-4)//^(@)C` ?
View SolutionWhen two non reactive samples at different temperatures are mixed in an isolated container of negligible heat capacity the final temperature of the mixture can be:
View SolutionTwo identical beakers with negligible thermal expansion are filled with water to the same level at `4^(@)C`. If one says `A` is heated while the other says `B` is colled, then:
View SolutionWhen m gm of water at `10^(@)C` is mixed with m gm of ice at `0^(@)C`, which of the following statements are false?
View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The coefficients of linear expansion of the strip goes up by `DeltaT`and the strip bends to from an arc of radius of curvature R. Then R is.
View SolutionThere is a rectangular metal plate in which two cavities in the shape of rectangle and circle are made, as shown with dimensions. `P` and `Q` are the centres of these cavities. On heating the plate, which of the following quantities increases?
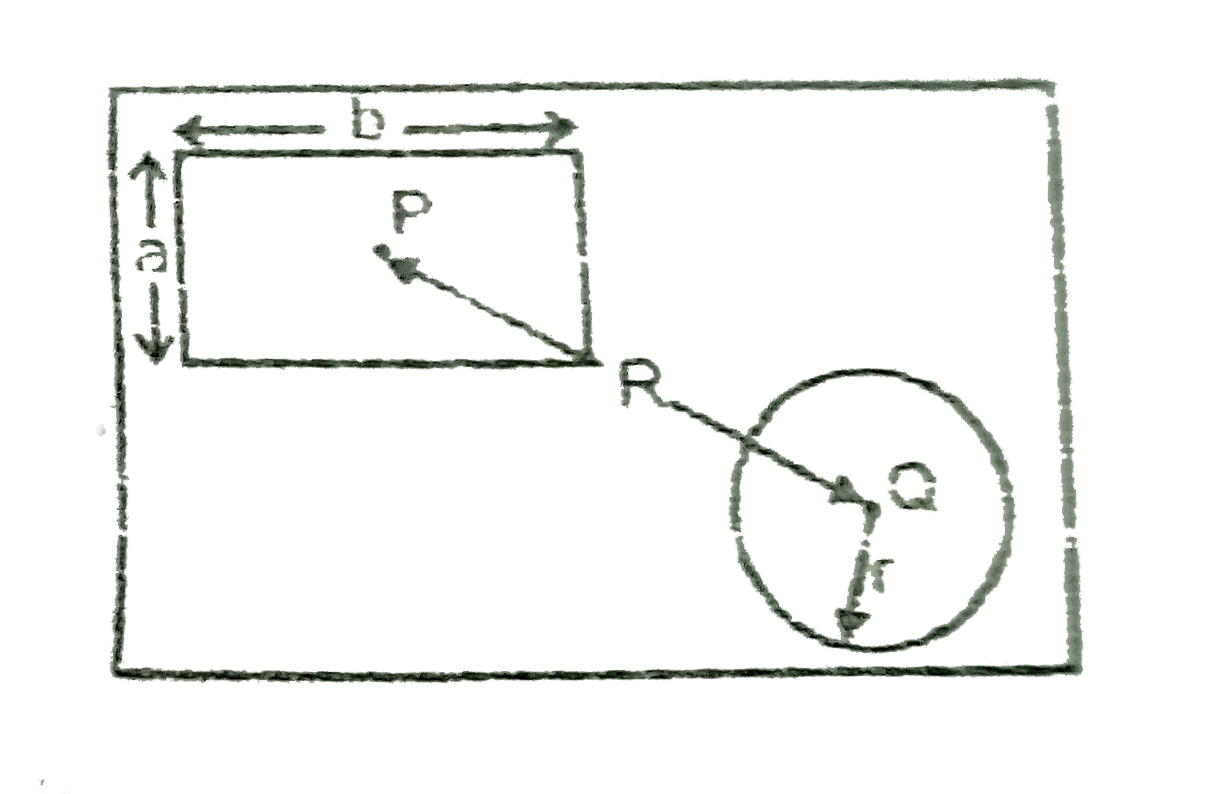
View Solution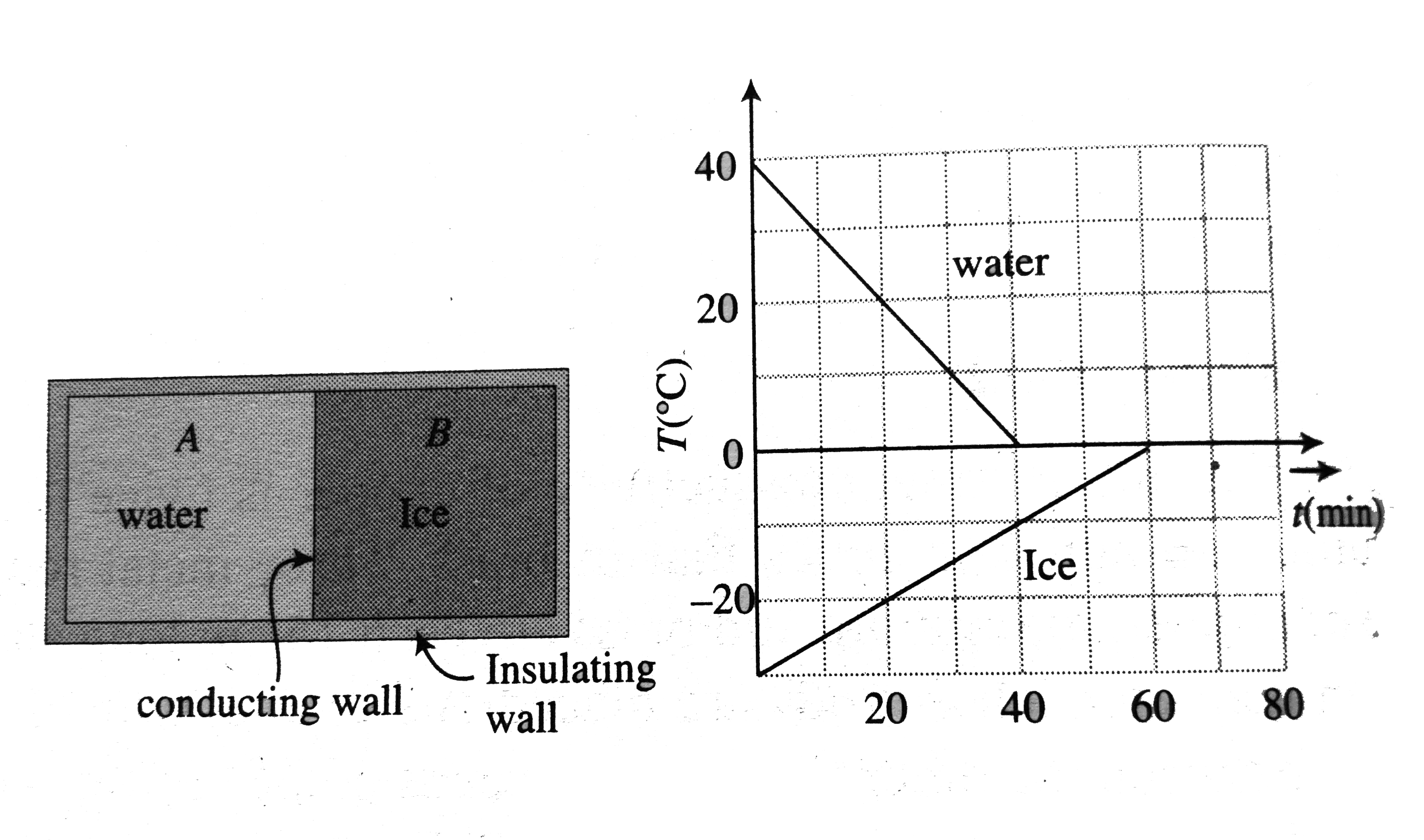
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice `=2100 J//kg-K`, specific heat of water `=4200 J//kg-K`, and latent heat of fusion of ice `=3.3xx10^5 J//kg`.
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartments A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice `=2100J//Kg-K` , specific heat of water `= 4200J//kg-K` and latent heat of fusion of ice `=3.3xx10^(5)J//kg`.
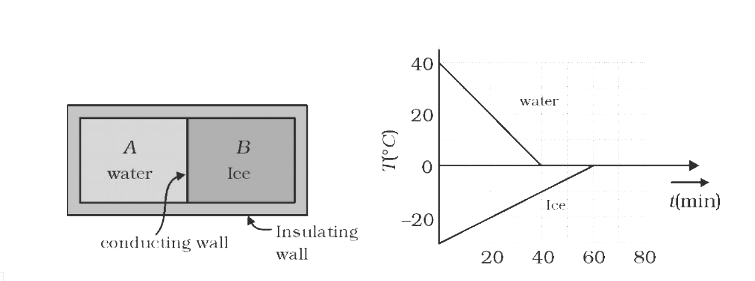
The initial mass of the ice in the container is equal to :
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartments A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice `=2100J//Kg-K` , specific heat of water `= 4200J//kg-K` and latent heat of fusion of ice `=3.3xx10^(5)J//kg`.
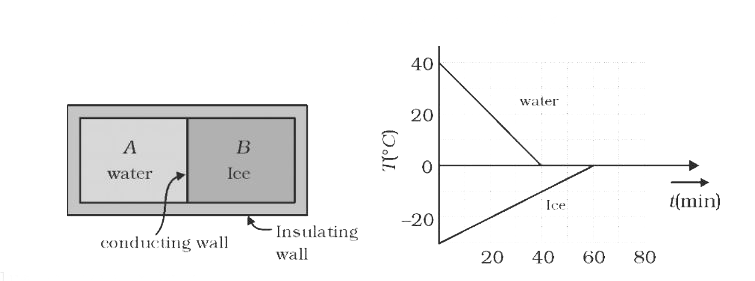
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to :
View SolutionIn a container of negligible heat capacity, `200 gm` ice at `0^(@)C` and `100gm` steam at `100^(@)C` are added to `200 gm` of water that has temperature `55^(@)C`. Assume no heat is lost to the surroundings and the pressure in the container is constant `1.0 atm`. (Latent heat of fusion of ice `=80 cal//gm`, Latent heat of vaporization of water `= 540 cal//gm`, Specific heat capacity of ice `= 0.5 cal//gm-K`, Specific heat capacity of water `=1 cal//gm-K)`
What is the final temperature of the system ?
View SolutionIn a container of negligible heat capacity `200` gm ice at `0^(@)`C and 100 gm steam at `100^(@)`C are added to 200 gm of water that has temperature `55^(@)`C. Assume no heat is lost to the surroundings and the pressure in the container is constant of `1.0atm (L_(f)=80 cal//gm,L_(v)=540cal//gm, s_(w)=1 cal//gm^(@)C)`
At the final temperature, mass of the total water present in the system, is
View SolutionIn a container of negligible heat capacity, `200 gm` ice at `0^(@)C` and `100gm` steam at `100^(@)C` are added to `200 gm` of water that has temperature `55^(@)C`. Assume no heat is lost to the surrpundings and the pressure in the container is constant `1.0 atm`. (Latent heat of fusion of ice `=80 cal//gm`, Latent heat of vaporization of water `= 540 cal//gm`, Specific heat capacity of ice `= 0.5 cal//gm-K`, Specific heat capacity of water `=1 cal//gm-K)`
Amount of the steam left in the system, is equal to
View Solution
Exercise questions and complete solutions for chapter CALORIMETRY AND THERMAL EXPANSION of RESONANCE ENGLISH of Class 11