Complete Solutions to Example of chapter CALORIMETRY AND THERMAL EXPANSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY AND THERMAL EXPANSION |
| RESONANCE | Example |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Heat required to increases the temperature of `1kg` water by `20^(@)C`
View SolutionFind the amount of heat released if `1kg` steam at `200^(@)C` is convered into `-20^(@)C` ice.
View SolutionAn iron block of mass `2kg`, fall form a height `10m`. After colliding with the ground it loses `25%` enegry to surroundings. Then find the temperature rise of block. (Take sp. Heat of iron `470 J//kg^(@)C)`
View SolutionThe temperature of equal masses of three different liquids `A, B`, and `C` are `10^(@)C 15^(@)C` and `20^(@)C` respectively. The temperature when `A` and `B` are mixed is `13^(@)C` and when `B` and `C` are mixed. It is `16^(@)C`. What will be the temperature when `A` and `c` are mixed?
View SolutionIf three different liquid of different masses specific heats and temperature are mixed with each other and then what is the temperature mixture at thermal equilibrium.
`m_(1),s_(1),T_(1) rarr` specification for liquid
`m_(2),s_(2),T_(2)rarr`specification for liquid.
`m_(3),s_(3),T_(3)rarr` specification for liquid.
View SolutionIn following equiation calculate value of H: 1kg ice at `-20^@C=H+1`kg water at `100^@C`, here H means heat required to change the state of substance.
View Solution`1 kg` ice at `-20^(@)C` is mixed with `1 kg` steam at `200^(@)C`. The equilibrium temperature and mixture content is
View SolutionA rectangular plate has a circular cavity as shown in the figure. If we increases its temperature then which dimension will increases in following figure.
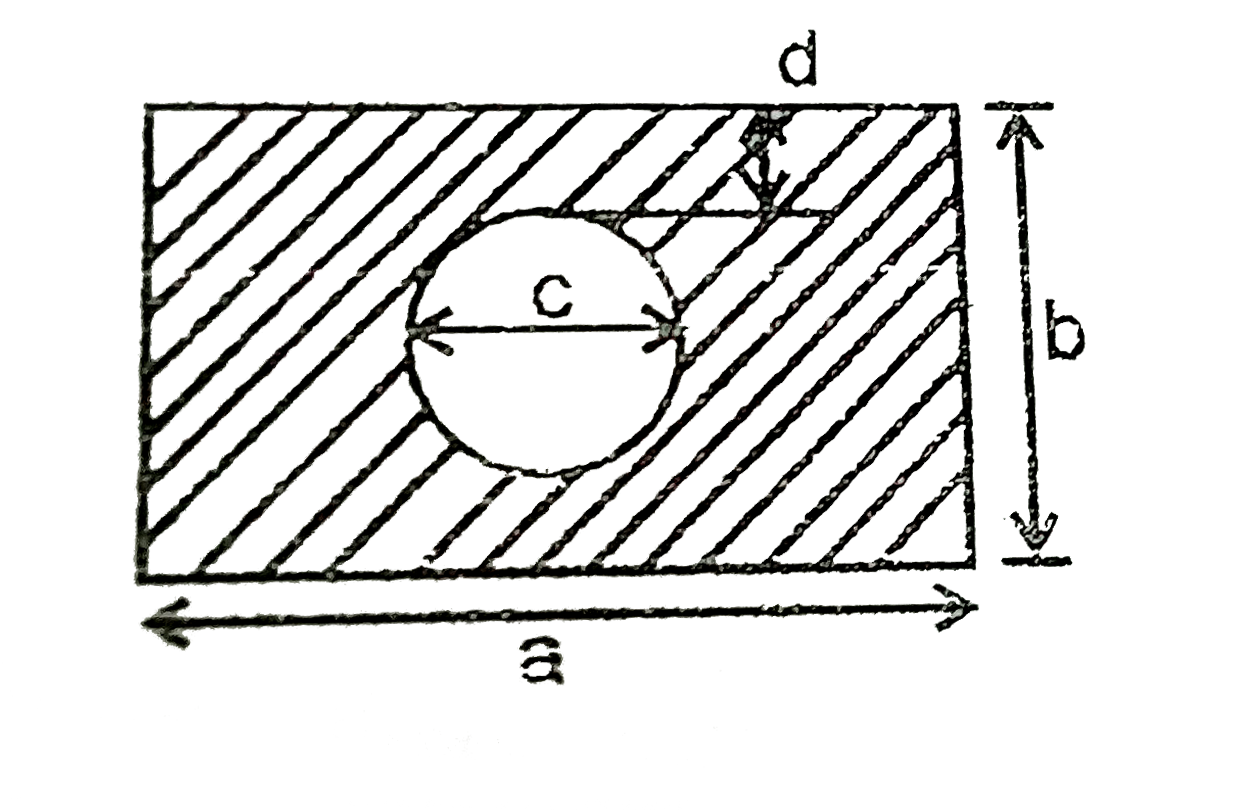
View SolutionIn the given figure, when temperature is increased then which of the following increases

(A) `R_(1)` (B) `R_(1)` (C )` R_(2) -R_(1)`
View SolutionWhat is the percentage change in length of `1m` iron rod it its temperature changes by `100^(@)C. alpha` for iron is `2 xx 10^(-5)//"^(@)C`.
View Solution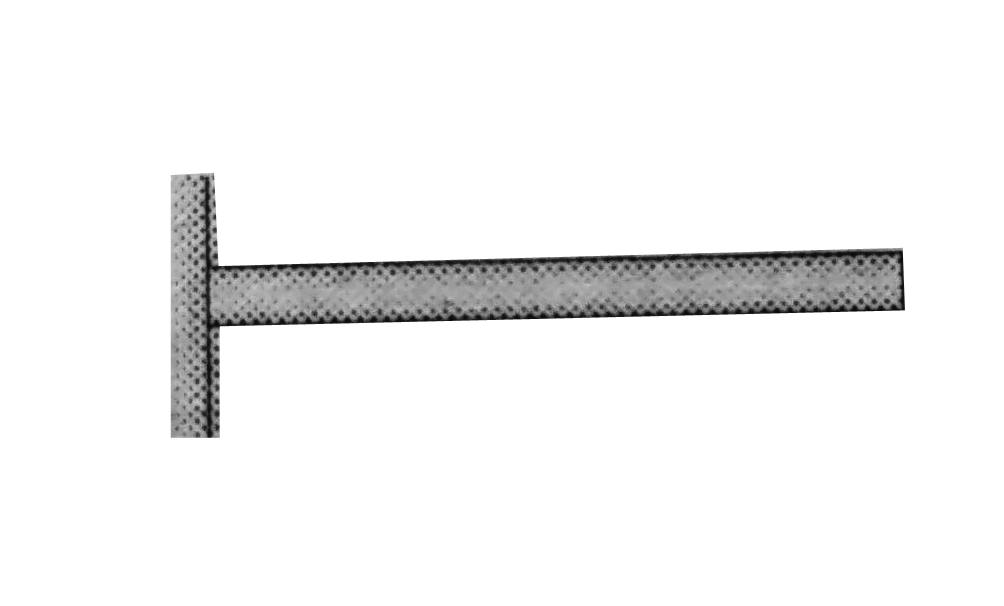
In the given figure, a rod is free at one end and other end is fixed. When we change the temperature of rod by `Deltatheta`, then strain produced in the rod will be
View SolutionAn iron ring measuring 15.00 cm in diameter is a be shrunk on a pulley which is 15.05 cm in diamer. All measurements refer to the room temperature `20^0 C`. To What minimum temperature should the ring be heated to make the job possible? Calculate the strain developed in the ring when in comes to the room temperature. Coefficient of linear expansion of iron `=12 xx 10^(-6) ^0 C^(-1)`.
View SolutionA steel rod of length 1 m rests on a smooth horizontal base. If it is heats from `0^@C` to `100^@C`, what is the longitudional strain developed?
View SolutionA steel rod is clamped at its two ends and rests on a fixes horizontal base. The rod is unstrained at `20^@C`. Find the longitudinal strain developed in the rod if the temperature rises to `50^@C`. Coefficient of linear expansion of steel `=1.2 xx 10^(-5 @)C^(-1)`.
View SolutionA steel wire of cross-sectional area `0.5mm^2` is held between two fixed supports. If the wire is just taut at `20^@C`, determine the tension when the temperature falls to `0^@C`. Coefficient of linear expansion of steel is `1.2 xx 10^(-5 @)C(-1)` and its Young's modulus is `2.0 xx 10^11 N m^(-2)`.
View SolutionA pendulum clock consists of an iron rod connected to a small, heavy bob. If it is designed to keep correct time at `20^(0) C`, how fast or slow will it go in 24 hours at `40^(0) C?` Coefficient of linear expansion of iron `= 1.2 xx 10^(-5)C^(-1)`.
View SolutionA bar measured with a vernier caliper is found to be 180 mm long. The temperature during the measurement is `10^@C`. The measurement error will be if the scale of the vernier caliper has been graduated at a temeprature of `20^@C`. (`alpha=1.1xx10^(-5).^(@)C^(-1)`. Assume that the length of the bar does not change.)
View SolutionA plane lamina has area `2m^(2)` at `10^(@)C` then what is its area at `110^(@)C` it's superficial expansion is `2 xx 10^(-5)//C`
View SolutionThe volume of a glass vessel is 1000 cc at `20^@C`. What volume of mercury could be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are `1.8 xx 10^(-4 @)C^(-1)` and `9 xx 10^(-6 @)C^(-1)` respectively.
View SolutionIf percentage change in length is `1%` with change in temperature of a cuboid object `(l xx 2l xx3l)` then what is precentage change in its area and volume.
View SolutionThe densities of wood and benzene at `0^(@)C` are `880 kg//m^(3)` and `900 kg//m^(3)` respectively. The coefficients of volume expansion are `1.2 xx 10^(-3)//'^(@)C` for wood and `1.5 xx 10^(-3)//'^(@)C` for benzene. At what temperature will a piece of wood just sink in benzene?
View SolutionA glass vessel of volume `100 cm^(3)` is filled with mercury and is heated from `25^(@)C to 75^(@)C`. What volume of mercury will overflow? Coefficient of linear expansion of glass `= 1.8 xx 10^(-6)//'^(@)C` and coefficeient of volume expansion of mercury is `1.8 xx 10^(-4)//'^(@)C`.
View SolutionA body is float inside liquid. If we increase temperature then what changes occur in buyancy force? (Assume body is always in floating condition)
View SolutionIn previous question discuss the case when body move downward, upwards and remains at same position when we increases temperature.
View SolutionThe readings of a thermometer at `0^(@)C` and `100^(@)C` are `50 cm` and `75 cm` of mercury column respectively. Find the temperature at which its reading is `80 cm` of mercury column ?
View Solution
Example questions and complete solutions for chapter CALORIMETRY AND THERMAL EXPANSION of RESONANCE ENGLISH of Class 11