Complete Solutions to Example of chapter MOTION IN STRAIGHT LINE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN STRAIGHT LINE |
| AAKASH INSTITUTE | Example |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
What is the state of a person sitting in a moving bus w.r.t. a person standing at the bus stand and why?
View SolutionA person walks along a semicircular path from A to B as shown in the figure given below.
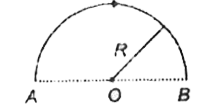
Calculate the distance and displacement traversed by the person.
View SolutionIf distance coverd by a particle is zero , what can be its displacement ?
View SolutionDisplacement of a person moving from A to B along a semicircular path of radius R is 100 m. What is the distance travelled by him ?
View SolutionDraw the position-time graph of a stationary object.
View SolutionDraw the x-t graph of an object in uniform motion.
View SolutionAn object was at x = 50 m at t = 0, then it starts moving uniformly towards origin at time t = 5 s. It is at origin. Draw the position versus time (x-t) graph for the object under this situation.
View SolutionRam covers a distance of 100 km with variable speed. During the first half of his journey his speed was 20 km/h and during the rest of his journey his speed was 40 km/h. Calculate the average speed of Ram during the whole course of his motion.
View SolutionWhat is the significance of average velocity or average speed?
View SolutionDistinguish between average speed and average velocity.
View SolutionWhat is the difference between average velocity and instantaneous velocity?
View SolutionThe displacement x of an object is given as a function of time `x=2t+3t^(2)`
Calculate the instantaneous velocity of the object at t = 2 s
View SolutionDraw the position-time graph of an object moving with positive accceleration.
View SolutionThe velocity of an object changes from 50 m/s to 60 m/s in 20 seconds. What is the average acceleration of the object over that interval?
View SolutionDraw the velocity-time graph of an object whose speed is increasing at uniform rate but moving with negative acceleration.
View SolutionThe position of a particle along the x-axis is given by the equation, `x=t^(3)-6t^(2)+9t`, where t is measured in seconds and x in meters.
(a) Find the velocity at time t
(b) What is the velocity at t = 2 s, at = t = 4 s?
(c) What is the time instant, when particle is at rest?
View SolutionA particle is moving along x-axis such that its velocity varies with time according to `v=(3m//s^(2))t-(2m//s^(3))t^(2)`. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionAn object moves along x-axis such that its position varies with time according to the relation `x=50t-5t^(2)`
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.
View SolutionThe position of a particle varies with time according to the relation `x=3t^(2)+5t^(3)+7t`, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View SolutionThe position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
View SolutionThe position of a particle is represented by the following equation.
`x=3t^(3)+7t^(2)+5t+8`
where x is in metres and t in seconds. Find the acceleration of the particle at t = 1 s.
Strategy : `v=(dx)/(dt) and a=(dv)/(dt)`
View SolutionThe acceleration a of a particle starting from rest varies with time according to relation, `a=alphat+beta`. Find the velocity of the particle at time instant t.
Strategy : `a=(dv)/(dt)`
View SolutionThe motion of a body is given by the equation `(dv)/(dt)=4-2v`, where v is the speed in m/s and t in second. If the body was at rest at t = 0, then find
(i) The magnitude of initial acceleration
(ii) Speed of body as a function of time
View SolutionThe position of an object moving on a straight line is defined by the relation `x=t^(3)-2t^(2)-4t`, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and t = 1 s.
View SolutionA car was movig at a rate of `18 kmh^(-1)` . When the brakes were applied, it comes to rest in a distance of 100 m. Calculate the retardation produced by the brakes.
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
`v=2t+3t^(2)`
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0
View SolutionAn object is thrwon vertically upwards with a velocity of 60 m/s. After what time it strike the ground ? Use `g=10m//s^(2)`.
View SolutionA stone is thrwon vertically upwards. On its way is passes point A with a speed v and passes point B, 30 m higher than A with speed `(v)/(2)`. Find (i) The speed v (ii) The maximum height reached by the stone above point B.
View SolutionA falling stone takes 0.25s to fall across a window which is 1 m high. From how far above the top of the window was the stone dropped (take `g=10m//s^(2)`)?
View SolutionAn object is thrown vertically upward with some speed. It crosses ` 2` points ` p,q` which are separated by (h) metre. If `t_(p)` is the time between `p` and highest point and coming back and ` t_(q)` is the time between `q` and highest point and coming back, relate acceleration due to gravity `t_(p),t_(q) and h`.
View SolutionA balloon starts rising from the ground with a constant acceleration of `1.25m//s^(2)`. After 8 s, a stone is released from the balloon. Find the time taken by the stone to reach the ground. (Take `g=10m//s^(2)`)
View SolutionIs it possible, that a body is moving with negative acceleration still speeding up? Given reason for your answer.
View SolutionA particle starts moving from position of rest under a constant acceleration. If it travels a distance x in t second, what distance will it travel in next t second?
View SolutionEngine of a train that is moving with unifrom acceleration passes a pole with speed `u` while the last compartment passes the pole with speed 'v'. The middle point of the train passes the given pole with speed:
View SolutionA particle starts with an initial velocity 2.0 m/s along the positive x-direction and it accelerations uniformly at the rate of `0.40m//s^(2)`
(a) Find the distance travelled by it in the first three seconds.
(b) How much time does it take to reach the velocity 9.0 m/s?
(c) How much distance will it cover in reaching the velocity 9.0 m/s?
View SolutionA passenger is standing d meters away from a bus. The bus beings to move with constant acceleration a. To catch the bus, the passenger runs at a constant speed v towards the bus, What must be the minimum speed of the passenger so that he may catch the bus?
View SolutionA particle, moving with uniform acceleration along a straight line ABC, crosses point A at t = 0 with a velocity 12 m/s. B is 40 m from A and C is 64 m from A. The particle passes B at t = 4 s.
(a) At what time, will the particle be C?
(b) What is its velocity at C?
View SolutionConsider the previous problem
(a) When does the particle reach A again?
(b) Locate the point where the particle reverses its direction of motion.
(c) Find the distance travelled by the particle in the first 15 seconds.
View SolutionA particle having initial velocity 4 m/s moves with a constant acceleration `1m//s^(2)` for a time interval of 10 second in straight line. Find the displacement of the particle in the last second and the distance travelled in 10 second.
View SolutionA particle travels a distance of 20 m in the `7^(th)` seconds and 24 m in `9^(th)` second. How much distance shall it travel in the `15^(th)` second?
View SolutionTwo trains having lengths 120 m and 100 m running in the opposite directions with velocities 40 km/h and 50 km/h. In what time they will completely cross each other?
View SolutionIn the given x - t graph. Find the position of an object at t = 3 second

View SolutionThe velocity - time graph for linear motion of an object is as shown. Find
(a) The distance travelled and
(b) Displacement for the interval between 5 s and 40 s.

View SolutionThe acceleration time graph of a particle is shown in the Fig. 2 (CF). 11. At time ` t= 0 s` velocity of the particle is ` 8 ms^(-1)`. Its velocity ` t= 10 s` is.
 .
.
View SolutionThe velocity-time graph is given below
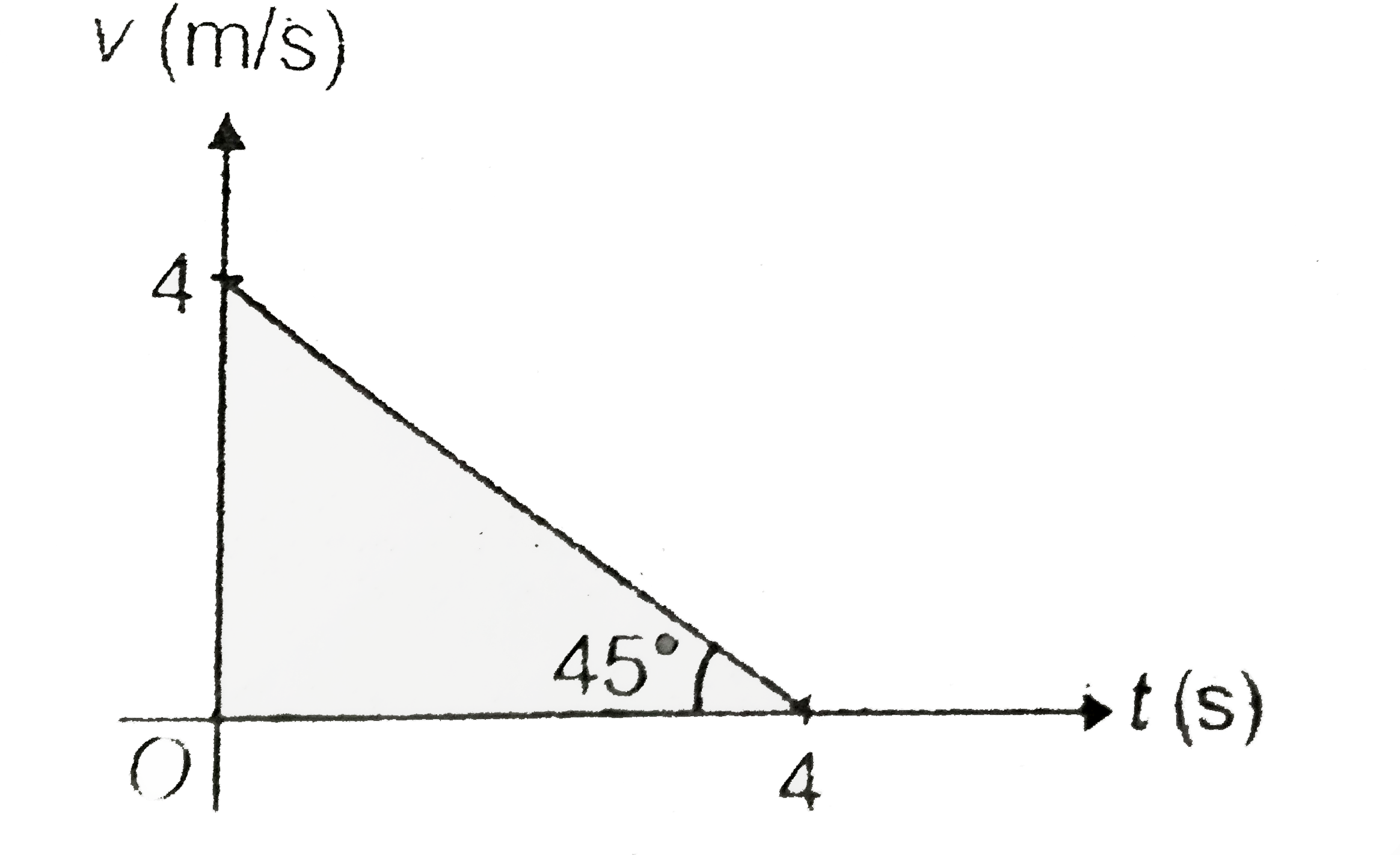
Draw the acceleration-time graph and position-time graph, given that at t = 0, particle is at origin.
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
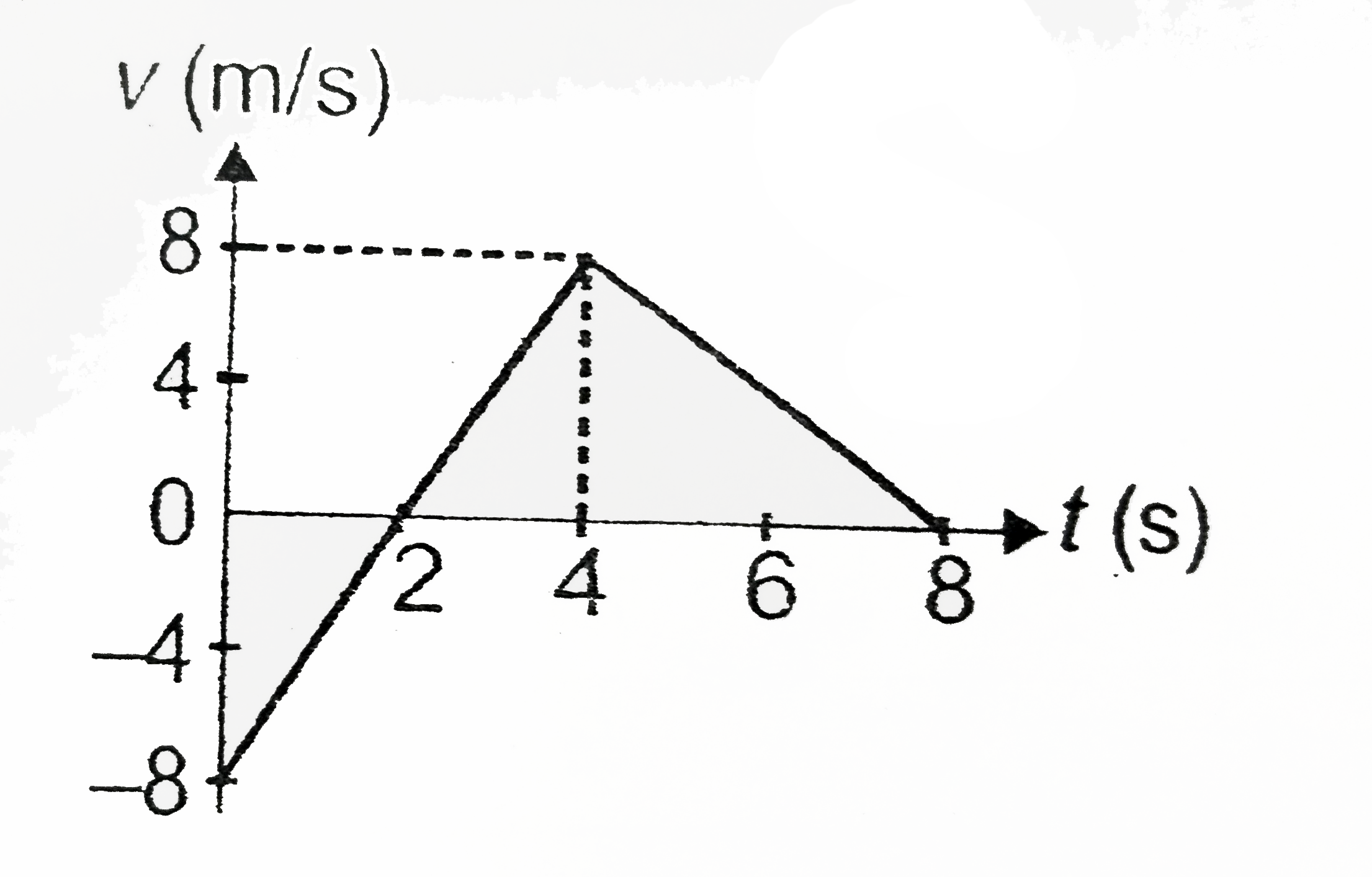
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionA particle starts from rest and accelerates constantly with `2m//s^(2)` for 10 s and then retards uniformly with same rate till it comes to rest. Draw the x-t, v-t and a-t graphs.
View SolutionAn object starts from rest from the point A to rest at point B on the same straight line at a distance d. It moves over the first part of the distance with an acceleration `alpha m//s^(2)` and for the remainder the retardation `beta m//s^(2)`. Find the time taken to complete the journey.
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
The distance between the boat and raft at a later instant of time t is
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
Let the boat turns back at time `t=t_(0)` and starts moving towards the raft. The separation between the raft and boat after a time interval t' measured from the moment of turning back is
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0. Let the boat turns back at time t = `t_(0)` and starts moving towards the raft.
After how much time, measured from the moment of turning back the boat will cross the raft again ?
Option 1 `t_(0)`
Option 2 `(ut_(0))/(u+v)`
Option 3 `(vt_(0))/(u+v)`
Option 4 `((v+v)t_(0))/(u-v)`
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
Let the boat turns back at time `t=t_(0)` and starts moving towards the raft. The separation between the raft and boat after a time interval t' measured from the moment of turning back is
View Solution
Example questions and complete solutions for chapter MOTION IN STRAIGHT LINE of AAKASH INSTITUTE ENGLISH of Class 12