Complete Solutions to Assignment (Section - D) Linked Comprehension Type Questions of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH INSTITUTE | Assignment (Section - D) Linked Comprehension Type Questions |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
Two particles `A` and `B` of mass `3kg` and `2kg` moving with speed `10m//s` and `5m//s` as shown in figure.
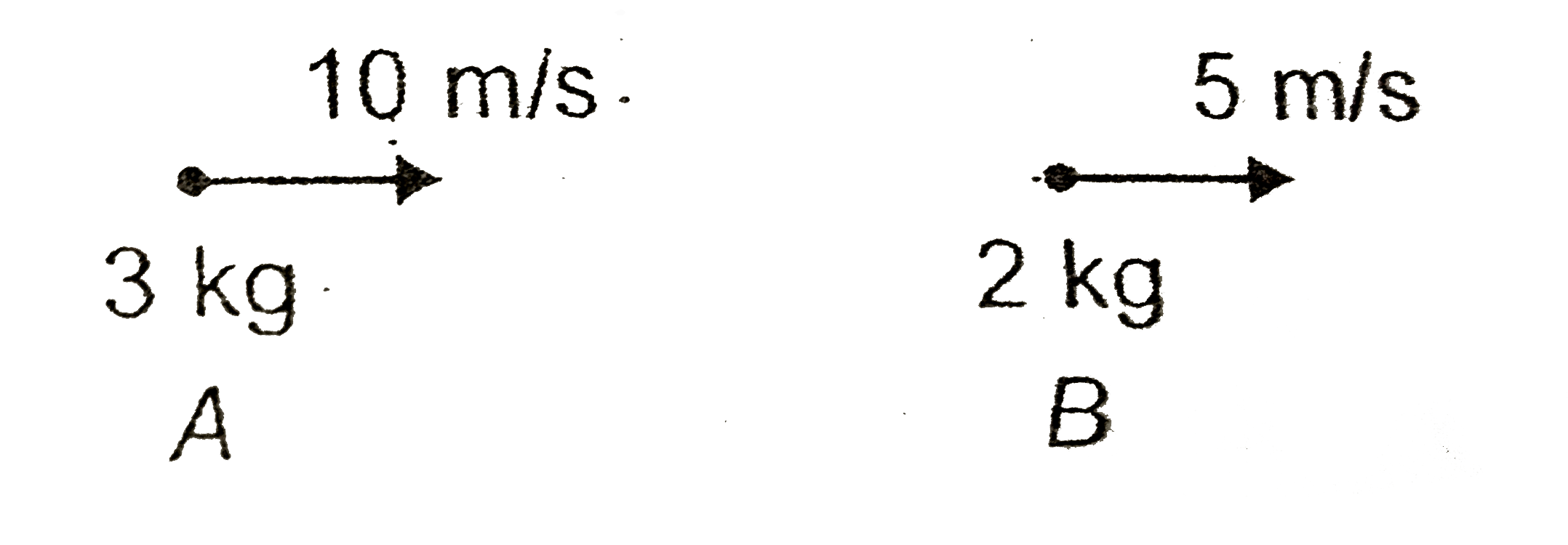
Find the maximum momentum that particles `A` can have after collision with `B`.
View SolutionTwo particles `A` and `B` of mass `3kg` and `2kg` moving with speed `10m//s` and `5m//s` as shown in figure.
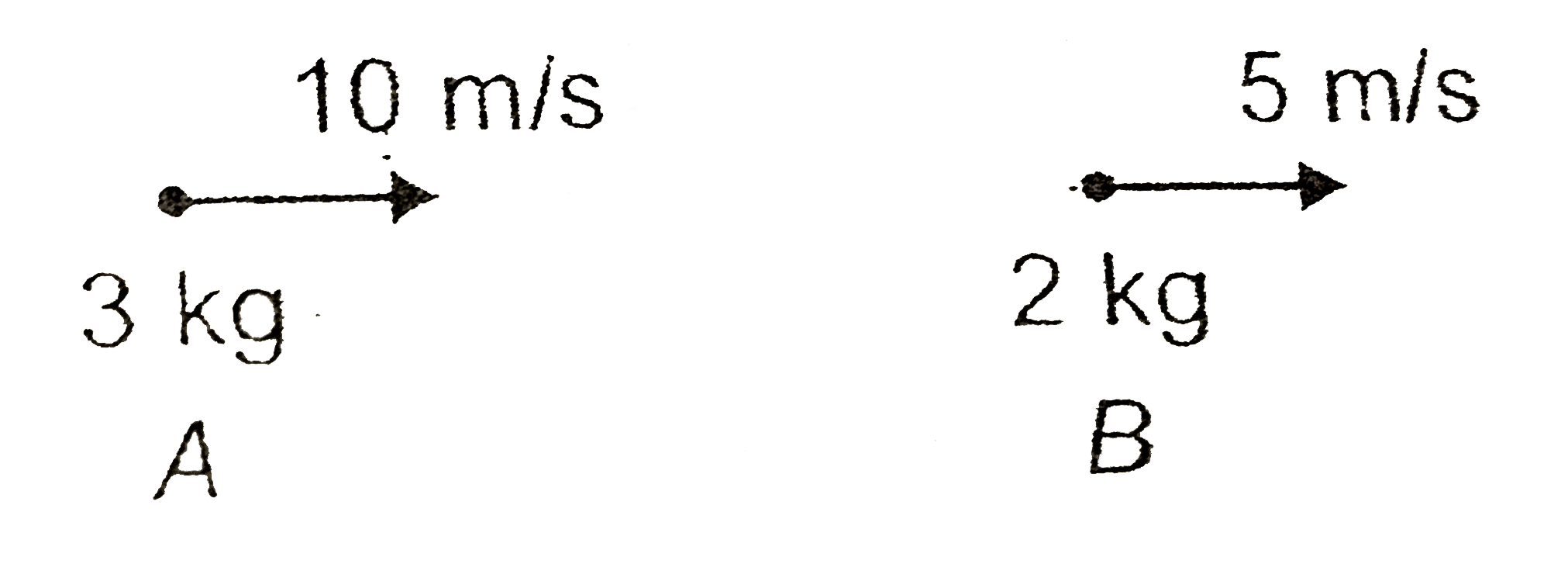
Find the maximum momentum that particle `B` can have after collision with A
View SolutionTwo particles `A` and `B` of mass `3kg` and `2kg` moving with speed `10m//s` and `5m//s` as shown in figure.
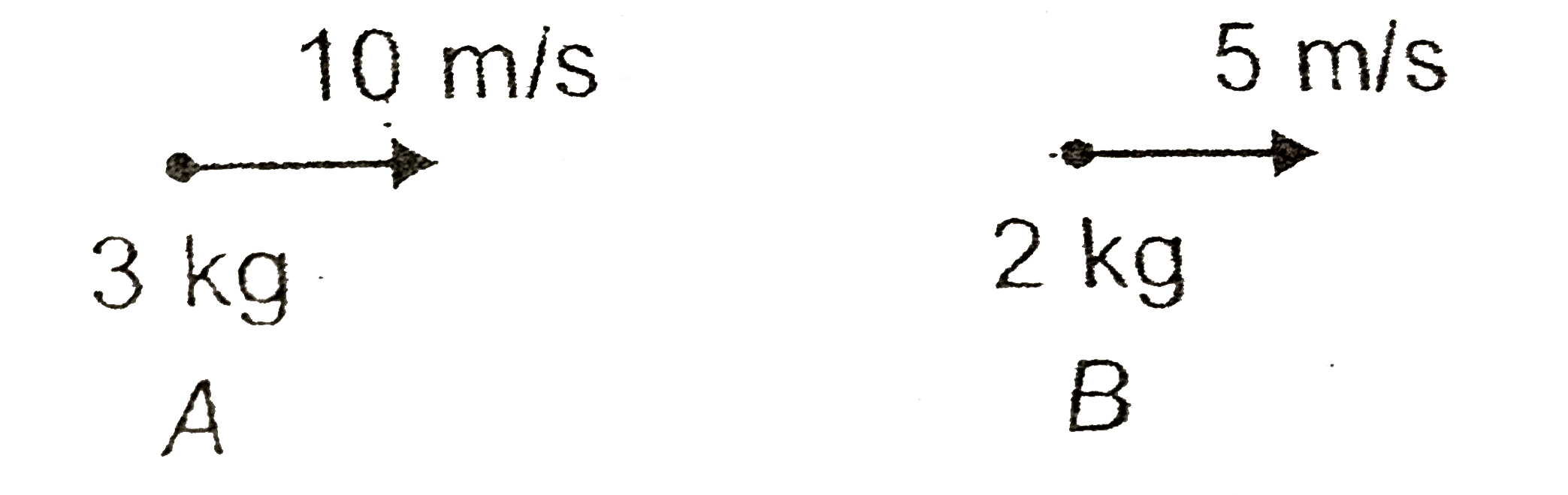
Kinetic energy of particle `A` when particle `B` has the maximum momentum
View SolutionTwo particles `A` and `B` of mass `3kg` and `4kg` moving on a smooth horizontal surface with speed `5m//s` and `2m//s` respectively collides each other. Coefficient of restitution is `e=(1)/(2)`, then
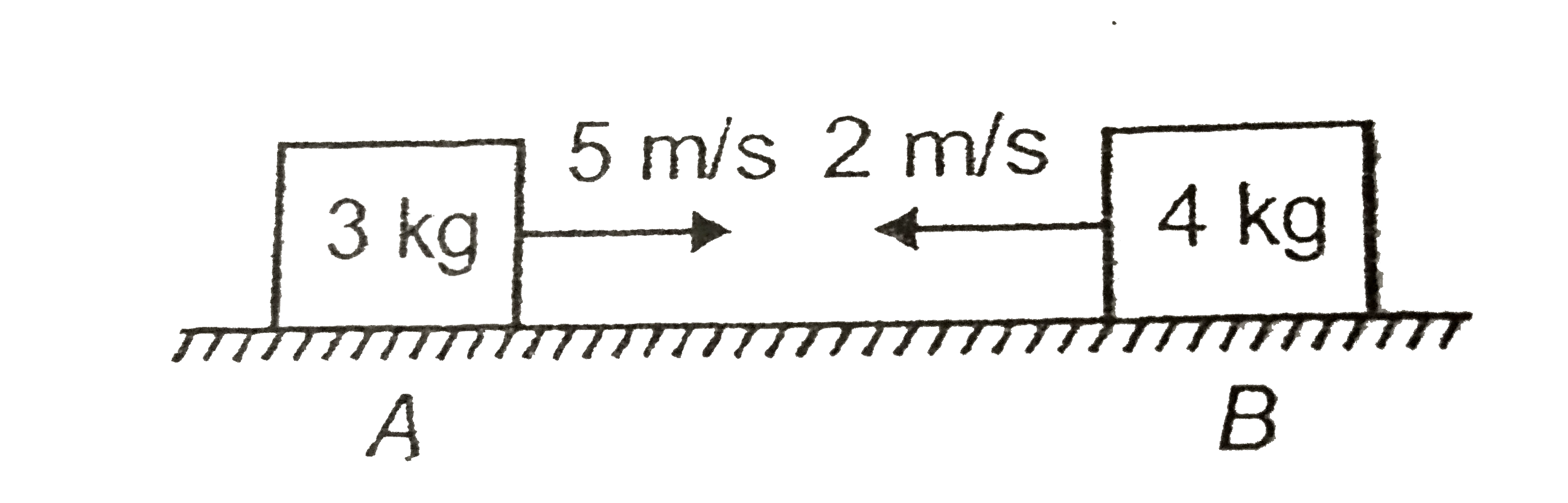
Velocity of `A` after collision
View SolutionTwo particles `A` and `B` of mass `3kg` and `4kg` moving on a smooth horizontal surface with speed `5m//s` and `2m//s` respectively collides each other. Coefficient of restitution is `e=(1)/(2)`, then

Velocity of `B` after collision
View SolutionTwo particles `A` and `B` of mass `3kg` and `4kg` moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is `e=(1)/(2)`, then

Loss in kinetic energy in collision
View SolutionTwo particles of mass `2m` and `m` moving with speed `v` and `2v` respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
View SolutionTwo particles of mass `2m` and `m` moving with speed `v` and `2v` respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
View SolutionTwo particles of mass `2m` and `m` moving with speed `v` and `2v` respectively pependicular to each other collides perfectly inelastically, then

Find the angle with the horizontal to which the particles move after collision.
View SolutionA rod `AB` of mass `M` and length `L` is shown in figure. End `A` of rod is hinged and end `B` is lying on the ground. Find the Normal reaction by ground on the rod

View SolutionA rod `AB` of mass `M` and length `L` is shown in figure. End `A` of rod is hinged and end `B` is lying on the ground. Find the Horizontal component of the force applied by the hinge

View SolutionA rod `AB` of mass `M` and length `L` is shown in figure. End `A` of rod is hinged and end `B` is lying on the ground. Find the Vertical component of the force applied by the hinge
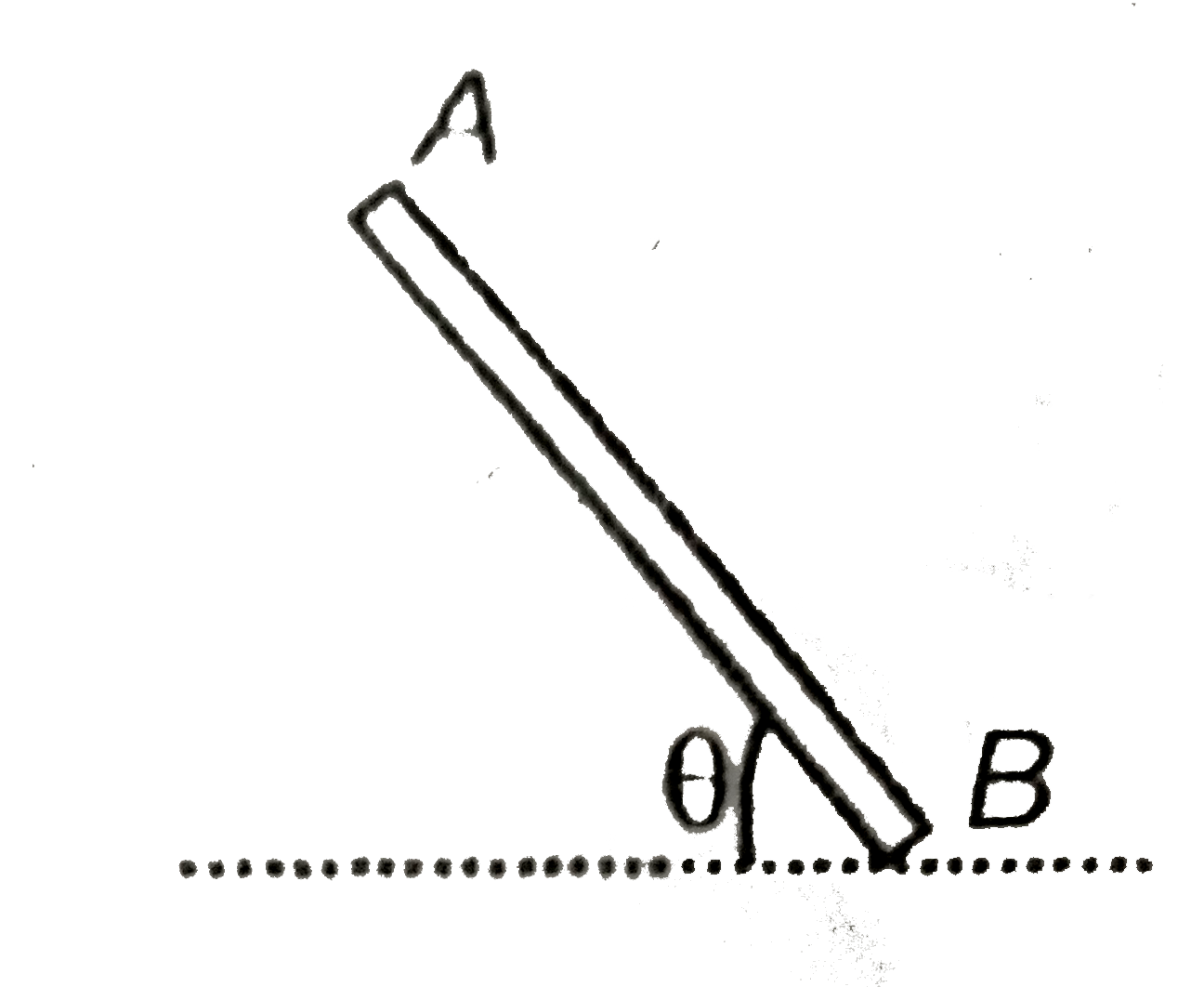
Vertical component of the force applied by the hinge
View SolutionA solid sphere of mass `m` and radius `R` is placed over a plank of same mass `m`. There is sufficient friction between sphere and plank to prevent slipping.When a horizontal force `F` is applied at centre of sphere, acceleration of the plank is

View SolutionA solid sphere of mass `m` and radius `R` is placed over a plank of same mass `m`. There is sufficient friction between sphere and plank to prevent slipping. Force of friction between sphere and plank is

View SolutionA solid sphere of mass `m` and radius `R` is placed over a plank of same mass `m`. There is sufficient friction between sphere and plank to prevent slipping.
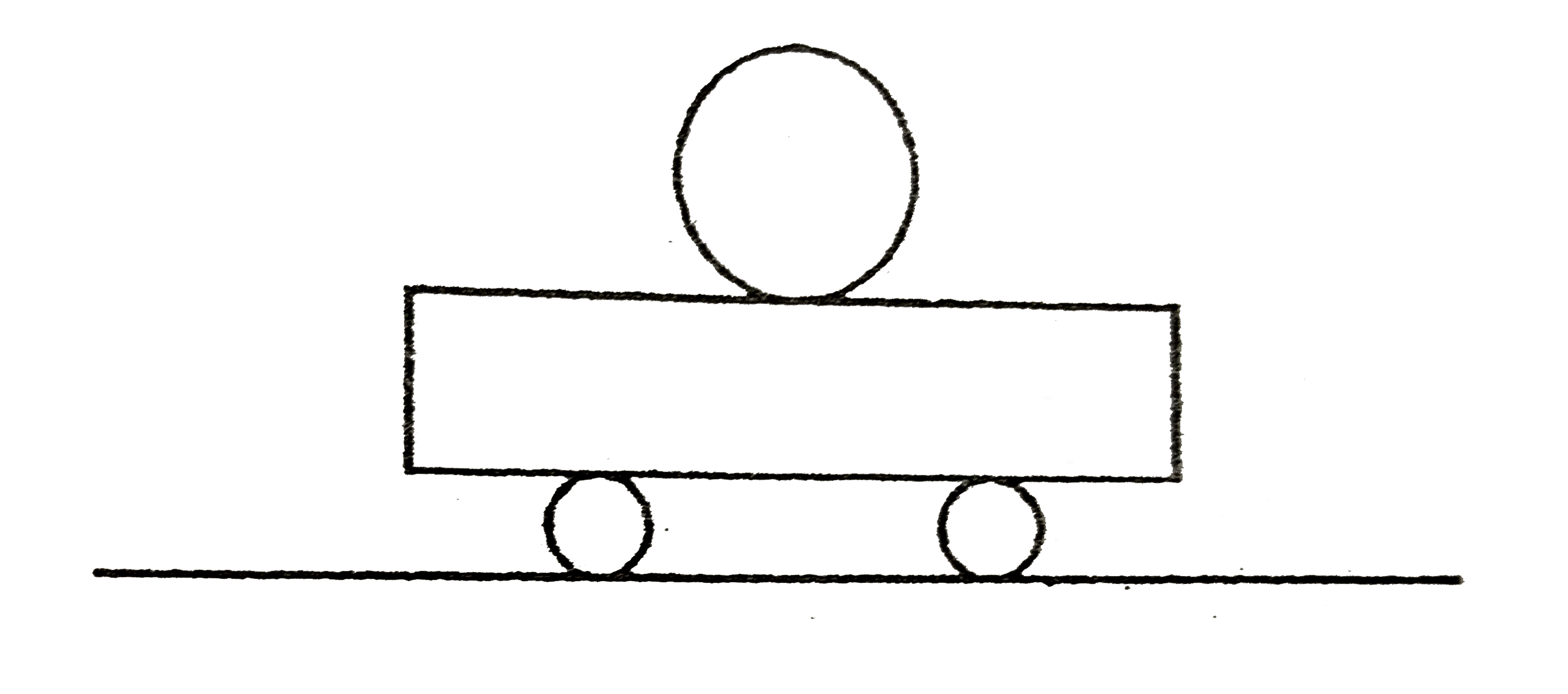
Acceleration of centre of mass of sphere is
View SolutionA solid sphere of mass `m` and radius `R` is placed over a plank of same mass `m`. There is sufficient friction between sphere and plank to prevent slipping.
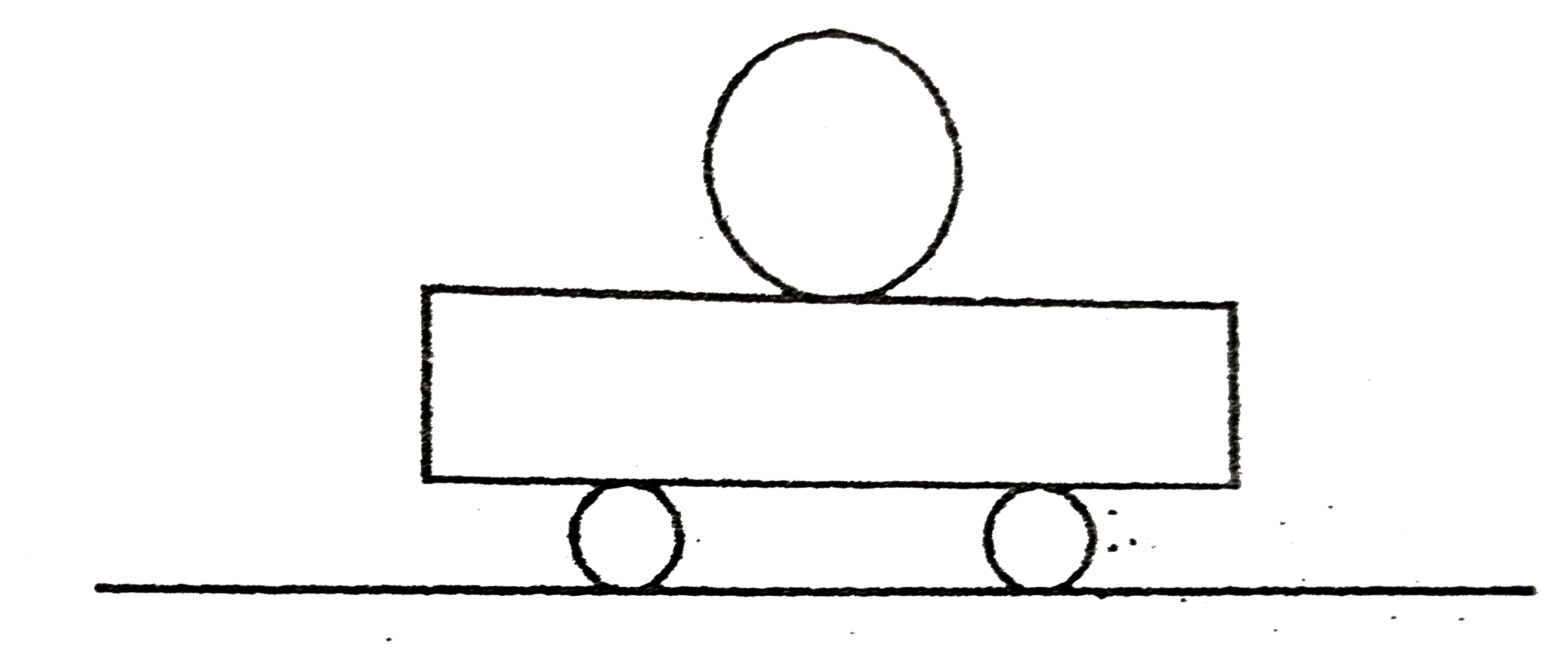
Angular acceleration of sphere is
View SolutionA solid sphere of mass `m` and radius `R` is placed over a plank of same mass `m`. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force `F` is applied on the plank. What is the maximum value of `F`, if `mu` is coefficient of friction between sphere movment and plank and there is no slipping ?
View SolutionA rod `AB` of length `2L` and mass `m` is lying on a horizontal frictionless surface. A particle of same mass `m` travelling along the surface hits the rod at distance `(L)/(2)` from `COM` with a velocity `v_(0)` in a direction perpendicular to rod and sticks to it.
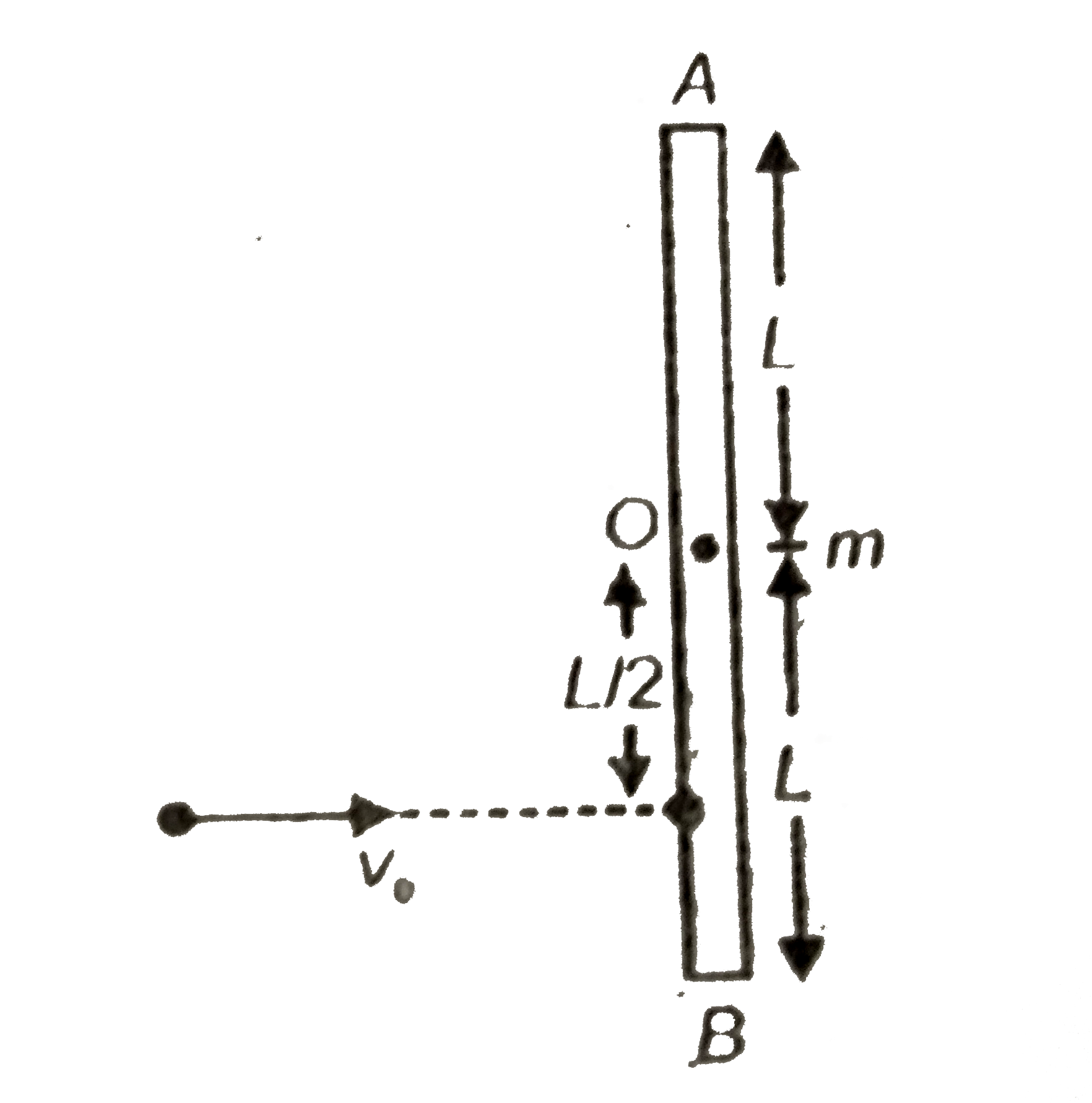
Angular velocity of rod just after collision is
View SolutionA rod `AB` of length `2L` and mass `m` is lying on a horizontal frictionless surface. A particle of same mass `m` travelling along the surface hits the rod at distance `(L)/(2)` from `COM` with a velocity `v_(0)` in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA rod `AB` of length `2L` and mass `m` is lying on a horizontal frictionless surface. A particle of same mass `m` travelling along the surface hits the rod at distance `(L)/(2)` from `COM` with a velocity `v_(0)` in a direction perpendicular to rod and sticks to it.
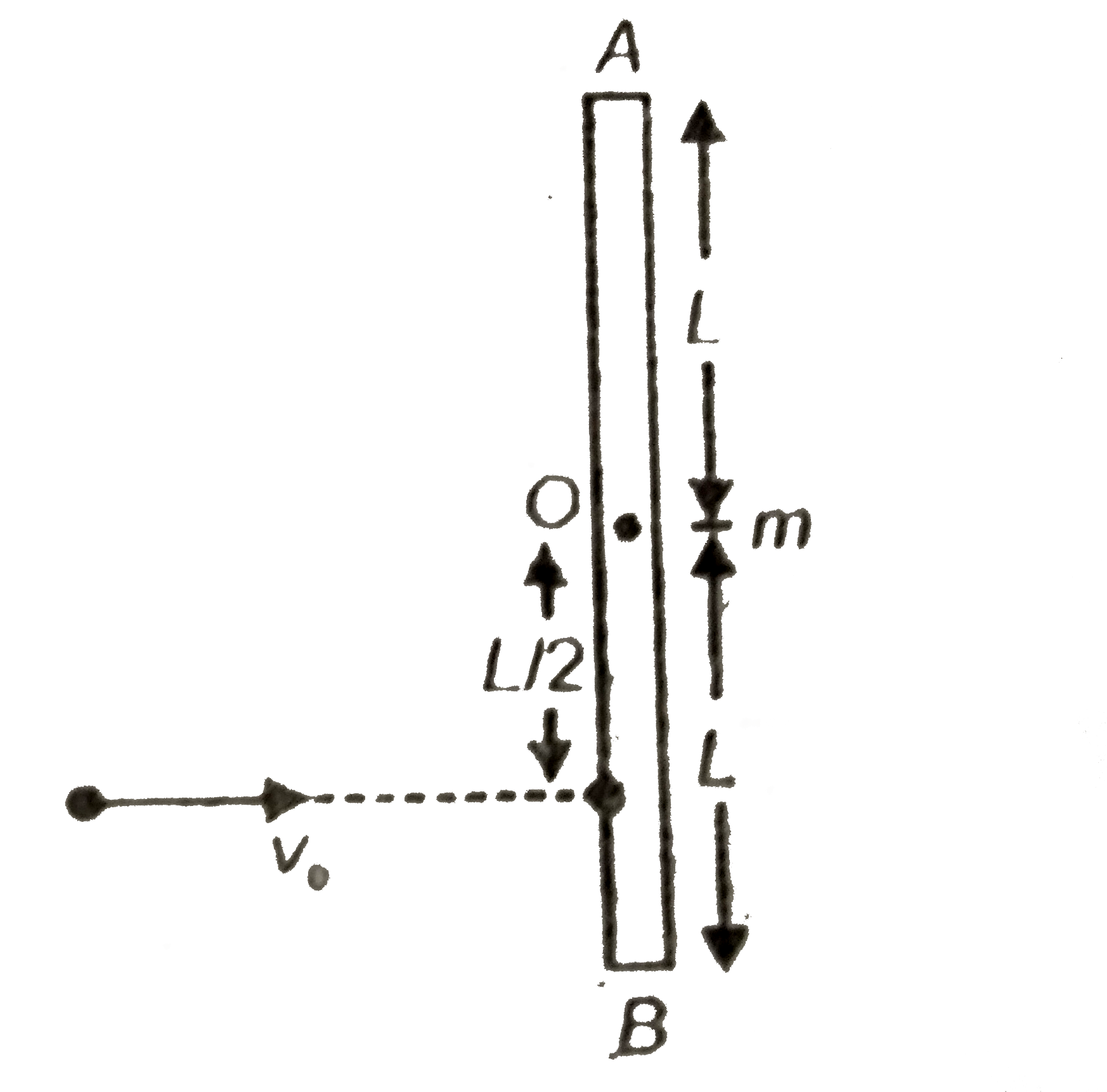
Distance of point `P` on rod from `B` which is at rest immediately afte collision is
View Solution
Assignment (Section - D) Linked Comprehension Type Questions questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- Assignment (Section - A) Objective Type Questions (One option is correct)
- Assignment (Section - B) Objective Type Questions (One option is correct)
- Assignment (Section - C) Objective Type Questions (More than one option are correct)
- Assignment (Section - D) Linked Comprehension Type Questions
- Assignment (Section - E) Assertion-Reason Type Questions
- Assignment (Section - F) Matrix-Match Type Questions
- Assignment (Section - G) Integar Type Questions
- Assignment (Section - H) Multiple True-False Type Questions
- Assignment (Section - I) Subjective Type Questions
- Assignment (Section - J) Aakash Challengers Questions
- Example
- Illustration
- Try Yourself