Complete Solutions to Assignment (Section - A) Objective Type Questions (One option is correct) of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH INSTITUTE | Assignment (Section - A) Objective Type Questions (One option is correct) |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
A circular plate of diameter `'a'` is kept in contact with a square plate of side a as shown. The density of the material and the thickness are same everywhere. The centre of mass of composite system will be
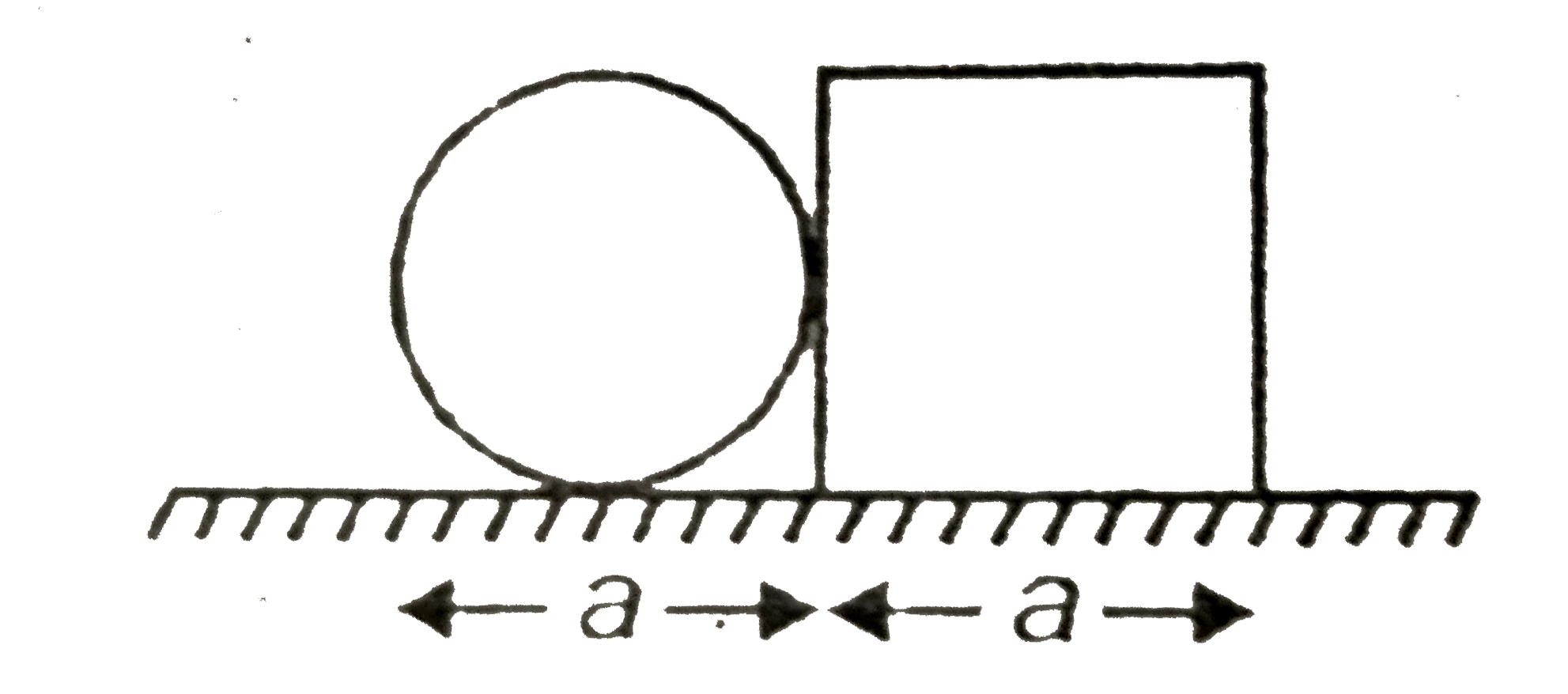
View SolutionA man of mass `m` is suspended in air by holding the rope of a ballon of mass `M`. As the man climbs up the rope, the ballon
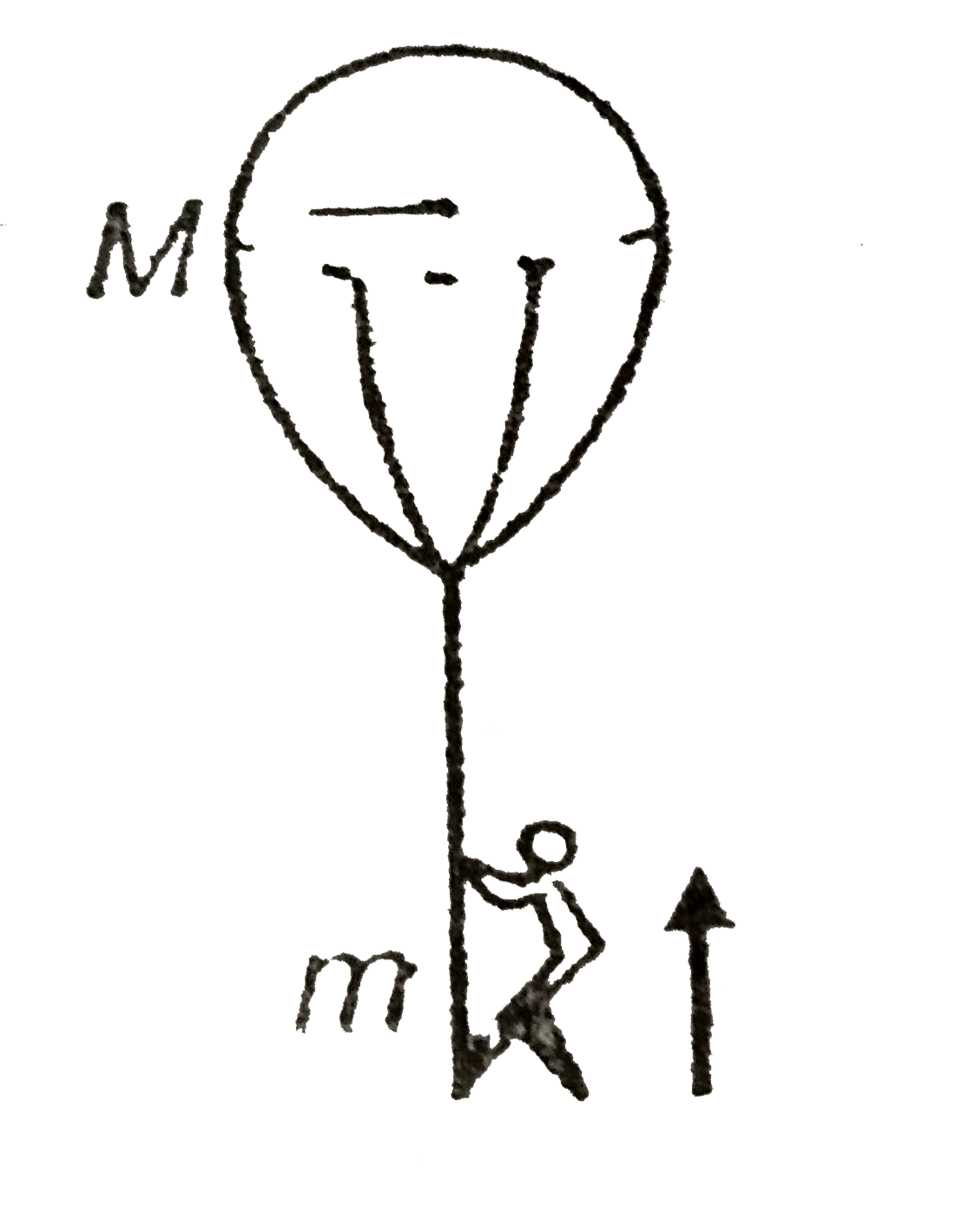
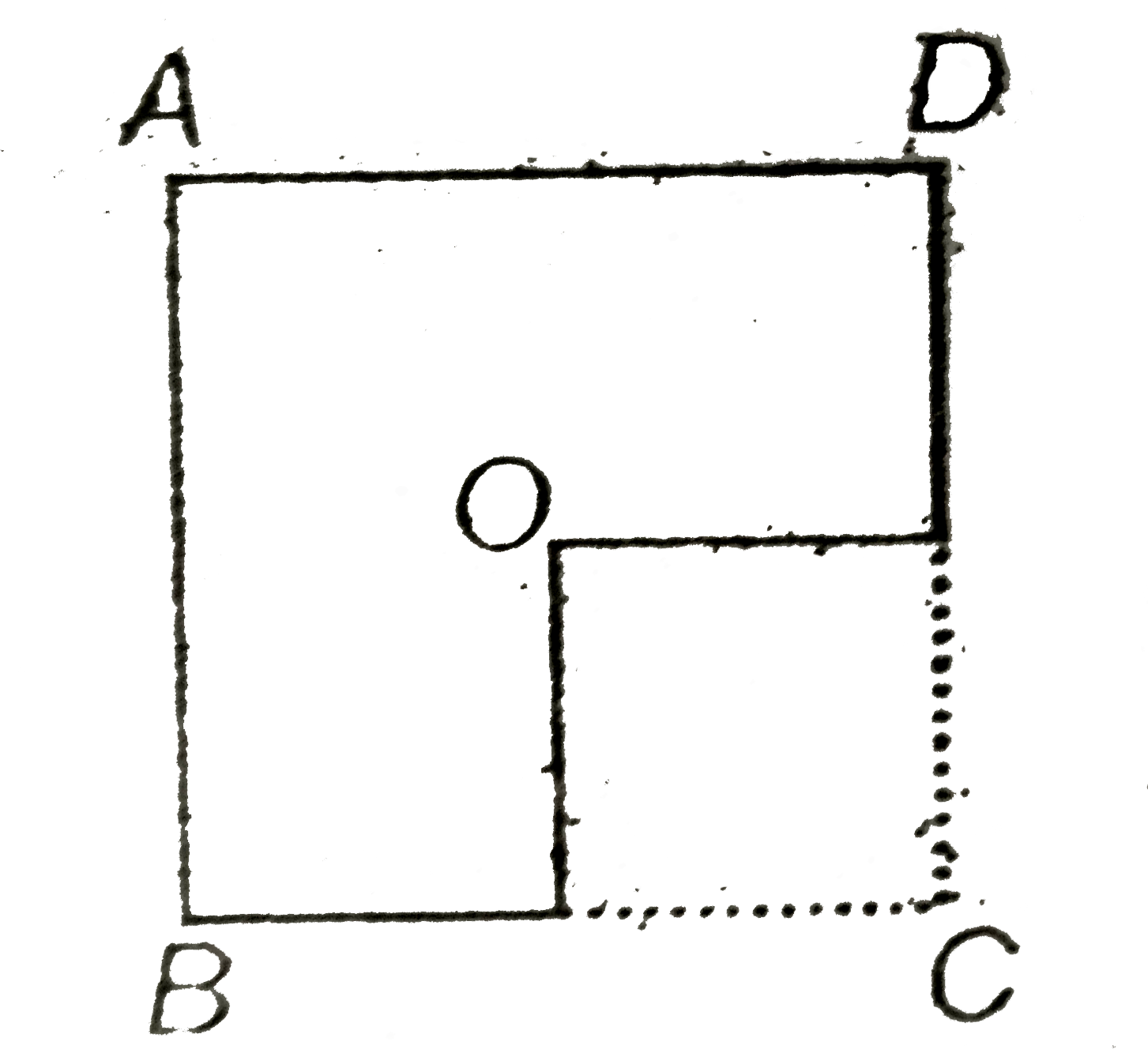
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on
View SolutionLocate the centre of mass of arrangement shown in figure. The three rods are identical in mass and length
View SolutionA particle of mass `m` is thrown horizontally from the top of a tower and anoher particle of mass `2m` is thrown vertically upward. The acceleration of centre of mass is
View SolutionA child is standing at one end of a long trolley moving with a speed v on a smooth horizontal floor. If the child starts running towards the other end of the trolley with a speed u, the centre of mass of the system (trolley + child) will move with a speed
View SolutionA man of mass `m` moves on a plank of mass `M` with a constant velocity `u` with respect to the plank, as shown in figure.
a.If the plank rests on smooth horizontal surface, determine the velocity of the plank. .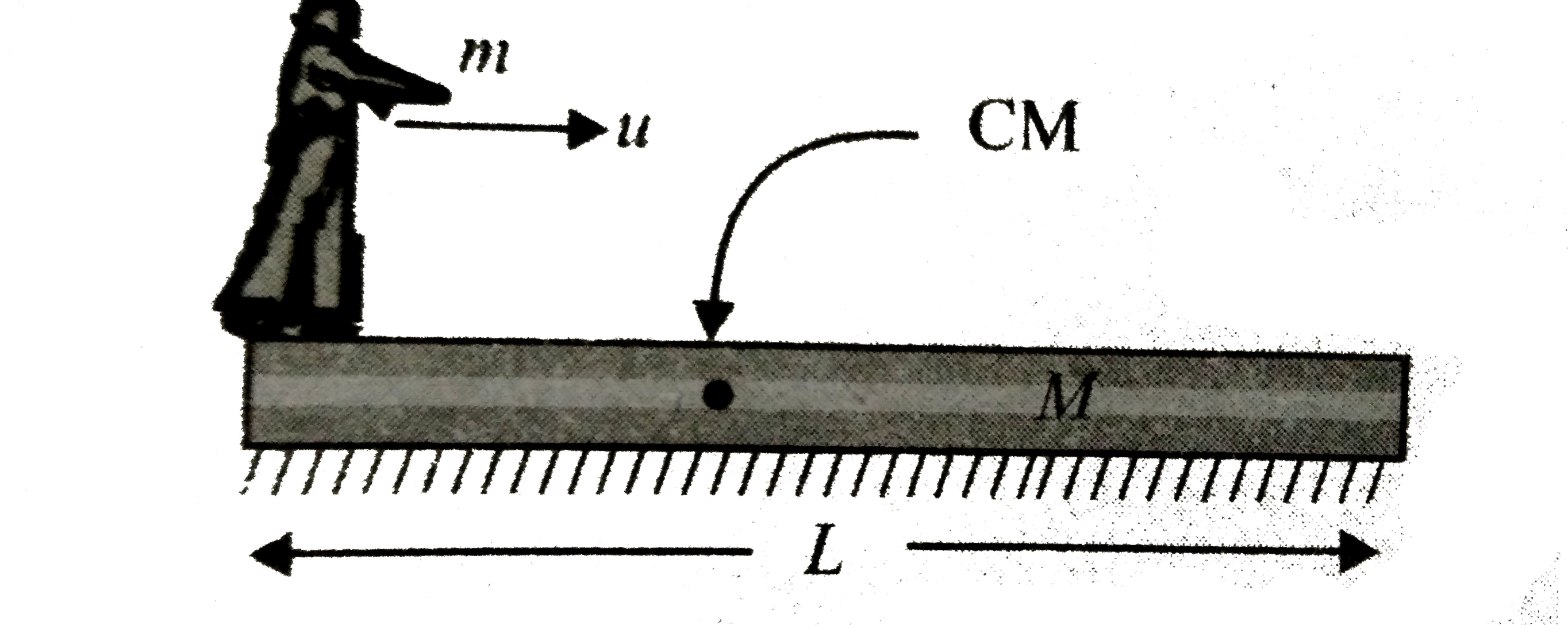
View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionA body falling vertically downwards under gravity breaks in two parts of unequal masses. The centre of mass of the two parts taken together shifts horizontally towards
View SolutionA body at rest breaks into two pieces of equal masses. The parts will move
View SolutionLet `I_(A) and I_(B)` be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionThe moment of inertia of a cylinder of mass `1000gm` and radius `20cm` about the axis `AB` shown in figure is

View SolutionThe angular momentum changes from `4` unit to `10` unit in `2` seconds. The torque is
View SolutionA constant torque of `400Nm` turns a wheel of moment of inertia `100kg m^(2)` about an axis through its centre. The angular velocity gained in `4` second is
View SolutionThe masses of two uniform discs are in the ratio `2 : 1` and their radii are in the ratio `1 : 2`. The ratio of their moments of inertia about the axis passing through their respective centres normal to plane is
View SolutionIf the torque acting on a system is zero then, which of the followin quantities is conserced ?
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is `I_(0)`. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionA rigid body of moment of inertia `l` has an angular acceleration `alpha`. If the instantaneous power is `P` then, the instantaneous angular velocity of the body is
View SolutionA flywheel rotates about a fixed axis and slows down from `300` r.p.m to `100` r.p.m in `2` minutes. The angular retardation of the flywheel (in `"radian"//"minute"^(2)`) is
View SolutionA body starting from rest gains an angular speed of `540` r.p.m in `6` second. The angular acceleration of the body is
View SolutionA ring of mass `6kg` and radius `40cm` is revolving at the rate of `300` rpm about an axis passing through its diameter. The kinetic energy of rotation of the ring is
View SolutionA ring of mass `10kg` and diameter `0.4m` is rotated about an axis passing through its centre. If it makes `1800` revolutions per minute then , the angular momentum of the ring is
View SolutionIf radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionA wheel whose moment of inertia is `10kgm^(2)` has an initial angular velocity of` 20 rad//s`. A constant torque of `20 Nm` acts on the wheel. The time in which wheel is acceleration to `100 rad//s` is
View SolutionTwo solid spheres are made up of the same material of density `rho`. The ratio of their radii is ` 1 : 2`. The ratio of their moments of inertia about their respective diameters is
View SolutionA fan of moment of inertia `0.6kgm^(2)` is moving with a speed of `0.5` r.p.s. The angular momentum of the fan is
View SolutionA hollow cylinder open at both ends slides without rotating, and then rolls without slipping with the same speed. The ratio of the kinetic energy in the two cases is (taken in order)
View SolutionA solid sphere of mas `2kg` rolls on a table with linear speed of `1 m//s`. Its total kinetic energy is
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is `200g cm^(2)`. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionA flywheel rotating about a fixed axis has a kinetic energy of `360J` when its angular speed is `30` radian `s^(-1)` . The moment of inertia of the wheel about the axis of rotation is
View SolutionWe have two spheres, one of which is hollow and the other solid. They have identical masses and moment of intertia about their respective diameters. The ratio of their radius is given by.
View SolutionThe moment of inertia of a body about a given axis is `1.2 kg m^(2)`. Initially, the body is at rest. In order to produce a rotational `KE` of `1500 J`, for how much duration, an acceleration of `25 rad s^(-2)` must be applied about that axis ?
View SolutionA solid cylinder of mass `20 kg` rotates about its axis with angular velocity of `100` radian `s^(-1)`. The radius of the cylinder is `0.25m`. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is
View SolutionIf `I_(1)` is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and `I_(2)` is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of `I_(1)` to `I_(2)` is
View SolutionA wheel of moment of inertia `30 kg m^(2)` is rotating at `10` rotations per minute. The work done in increasing its speed to `5` times its initial value will be
View SolutionA ring of mass `1kg` and radius `1m` is moving with a velocity of `1m//s` by rolling on a frictionless inclined plane. The total kinetic energy of the ring is
View SolutionA disc and a ring of the same mass are rolling down frictionless inclined plane, with the same kinetic energy. The ratio of the velocity of disc to the velocity of ring is
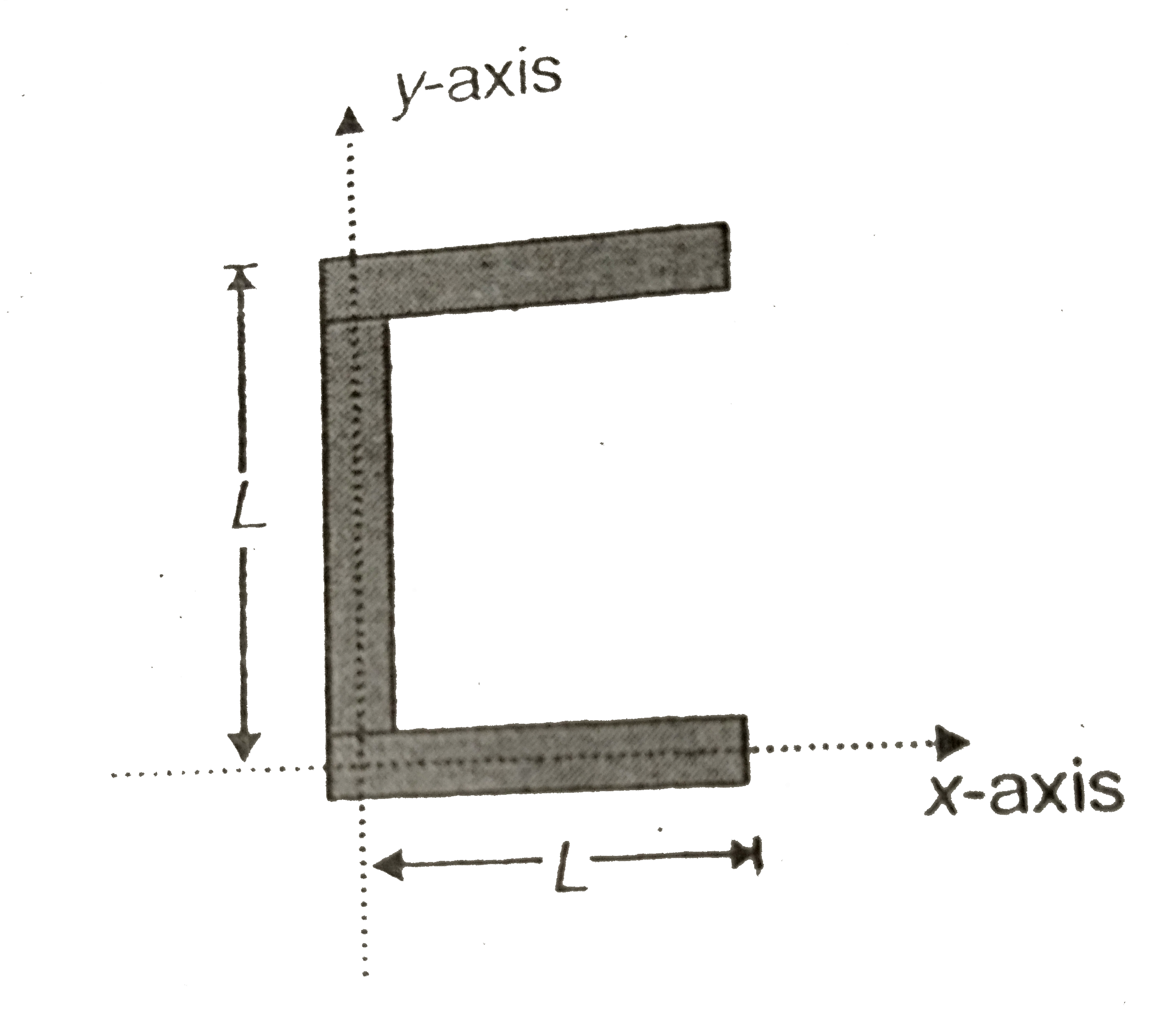
View SolutionThe moment of inertia of a thing uniform rod of length `L` and mass `M`, about axis `CD` (as shown in figure) is

View SolutionTwo bodies with moment of inertia `l_(1)` and `l_(2)` `(l_(1) gt l_(2))` have equal angular momentum. If `E_(1)` and `E_(2)` are the rotational kinetic energies, then
View SolutionFrom a circular disc of mass `M` and radius `R`, a part of `60^(@)` is removed. The `M.I.` of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
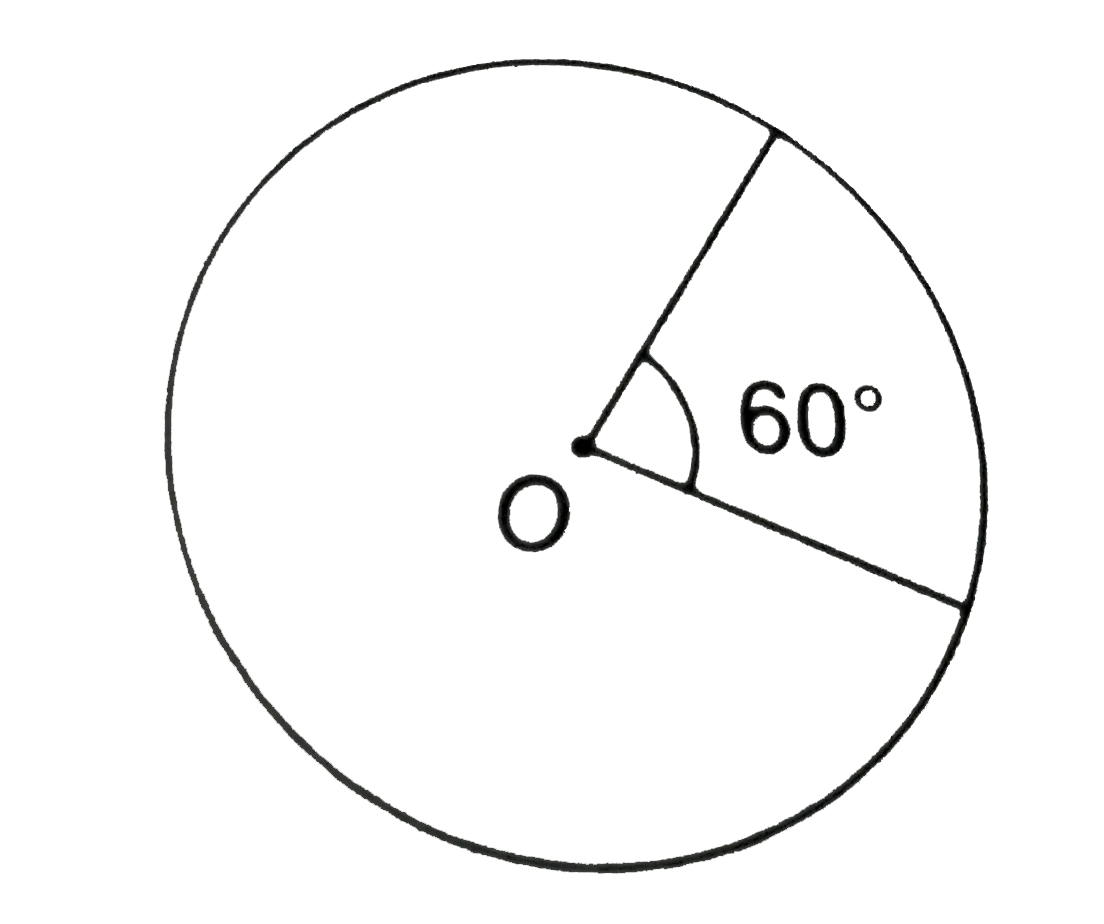
View SolutionA body is rolling without slipping on a horizontal plane. The rotational energy of the body is `40%` of the total kinetic energy. Identify the body
View SolutionThe angular velocity of a body is `vecomega=3hati+5hatj+6hatk("radian"//s)`. A torque `vectau=hati+2hatj+3hatk(Nm)` acts on it. The rotational power (in watt) is
View SolutionWhen a solid cylinder rolls without slipping the ratio of kinetic energy of translation to its total kinetic energy is
View SolutionThe torque required to stop a wheel having moment of inertia `5xx10^(-3)kgm^(2)` from a speed of `10` radian `s^(-1)` in `20s` is
View SolutionThe position vector of a point is `(3hati-2hatj+6hatk)m`. The `i^(th)` component of torque of force `(2hati+3hatj-6hatk)N` acting at the point about origin in `(Nm)` is
View SolutionA particle performing uniform circular motion gas angular momentum `L`. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
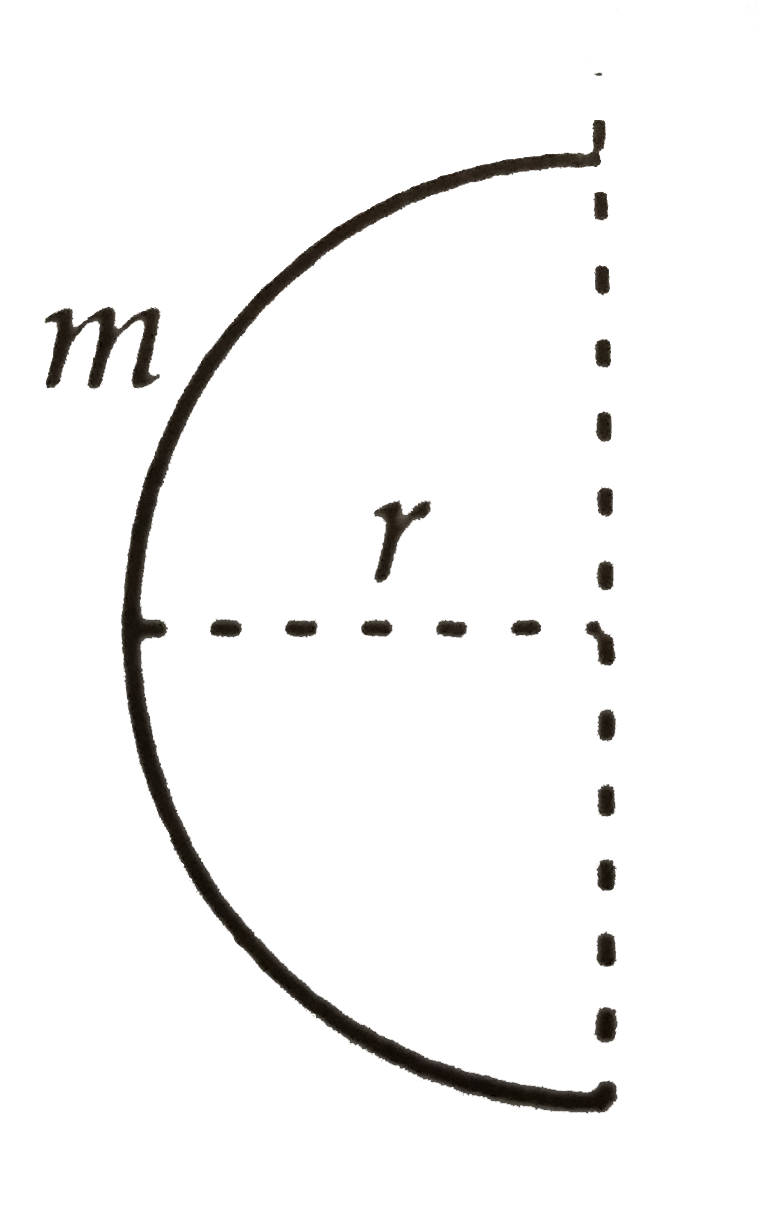
View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
View SolutionA constant torque acting on a uniform circular wheel changes its angular momentum from `A_(0)` to `2A_(0)` in `1s`. The magnitude of this torque is
View SolutionWhich of the following is correct ? (symbols have their ususal meanings)
View SolutionA dancer on ice spins faster when she folds her arms due to
View SolutionA solid sphere of radius `r` and mass `m` rotates about an axis passing through its centre with angular velocity `omega`. Its `K.E`. Is
View SolutionThe moment of inertia of a solid cylinder of density `rho`, radius of base `r`, and height `h` about an axis passing through its centre of mass and parallel to length is
View SolutionA person sitting firmly over a rotating stool has his arms stretched. If he folds his arms, his angular momentum about the axis of rotation
View SolutionRadius of gyration has the unit
View SolutionA bomb at rest explodes. The centre of mass
View SolutionIf `vecA*vecB=|vecAxxvecB|`. Then angle between `vecA` and `vecB` is
View SolutionWrite SI unit of angular momentum:
View SolutionIf `vecomega=2hati-3hatj+4hatk` and `vecr=2hati-3hatj+2hatk` then the linear velocity is
View SolutionThe moment of inertia of a body does not depend on
View SolutionA solid sphere, disc and solid cylinder all of the same mass and made of the same material are allowed to roll down (from rest) on the inclined plane, then
View SolutionA body of mass `m` slides down an smooth incline and reaches the bottom with a velocity, Now smooth incline surface is made rough and the same mass was in the form of a ring which rolls down this incline, the velocity of the ring at the bottom would have been:
View Solution
Assignment (Section - A) Objective Type Questions (One option is correct) questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- Assignment (Section - A) Objective Type Questions (One option is correct)
- Assignment (Section - B) Objective Type Questions (One option is correct)
- Assignment (Section - C) Objective Type Questions (More than one option are correct)
- Assignment (Section - D) Linked Comprehension Type Questions
- Assignment (Section - E) Assertion-Reason Type Questions
- Assignment (Section - F) Matrix-Match Type Questions
- Assignment (Section - G) Integar Type Questions
- Assignment (Section - H) Multiple True-False Type Questions
- Assignment (Section - I) Subjective Type Questions
- Assignment (Section - J) Aakash Challengers Questions
- Example
- Illustration
- Try Yourself