Complete Solutions to Assignment (Section - B) Objective Type Questions (One option is correct) of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH INSTITUTE | Assignment (Section - B) Objective Type Questions (One option is correct) |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
Two masses `2kg` and `5kg` are placed at points `'A'` and `'B'` as shown in the figure
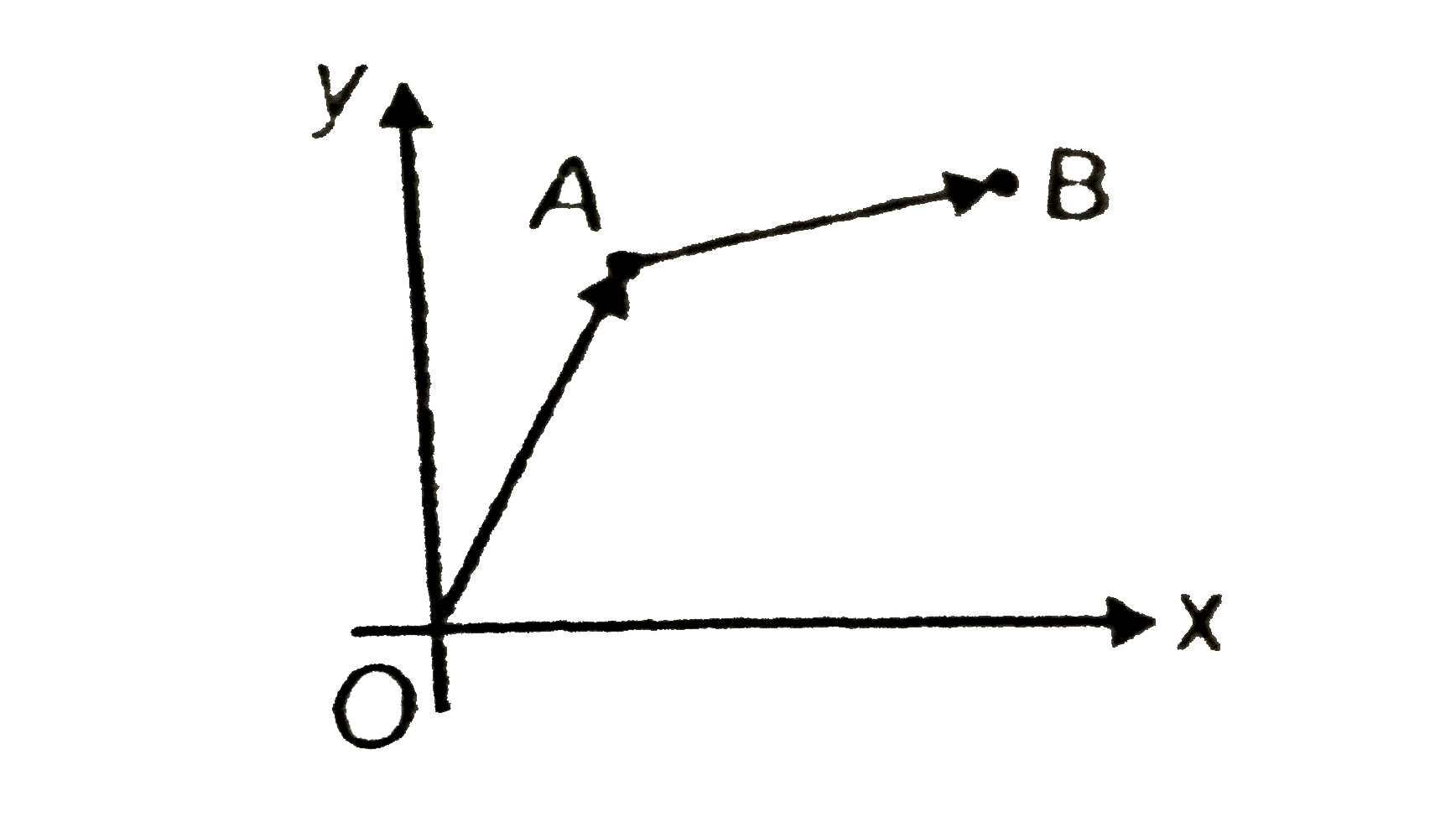
`vecOA=2hati+3hatj`
`vecAB=5hati+8hatj`
Find the co-ordinates of centre of mass.
View SolutionA shell following a parabolic path explodes somewhere in its flight. The centre of mass of fragements will move in
View SolutionThe velocity of the centre of mas of the system of two particle each of mass `2kg`, as shown in figure, is

View SolutionWhen a stick of length `L` mass `M` intially upright on a fricitionless floor starts falling the
View SolutionIf two particles of masses `m_(1)` and `m_(2)` are projected vertically upwards with speed `v_(1)` and `v_(2)`, then the acceleration of the centre of mass of the system is
View SolutionTwo partticles `A` and `B` intially at rest move towards each other under a mutual force of attraction. The instant at which velocity of `A` is `4v` and velocity of `B` is `2v`, the velocity of centre of mass of the system at that instant will be
View SolutionA rod of length `2l` is bent as shown in figure. Coordinates of centre of mass are
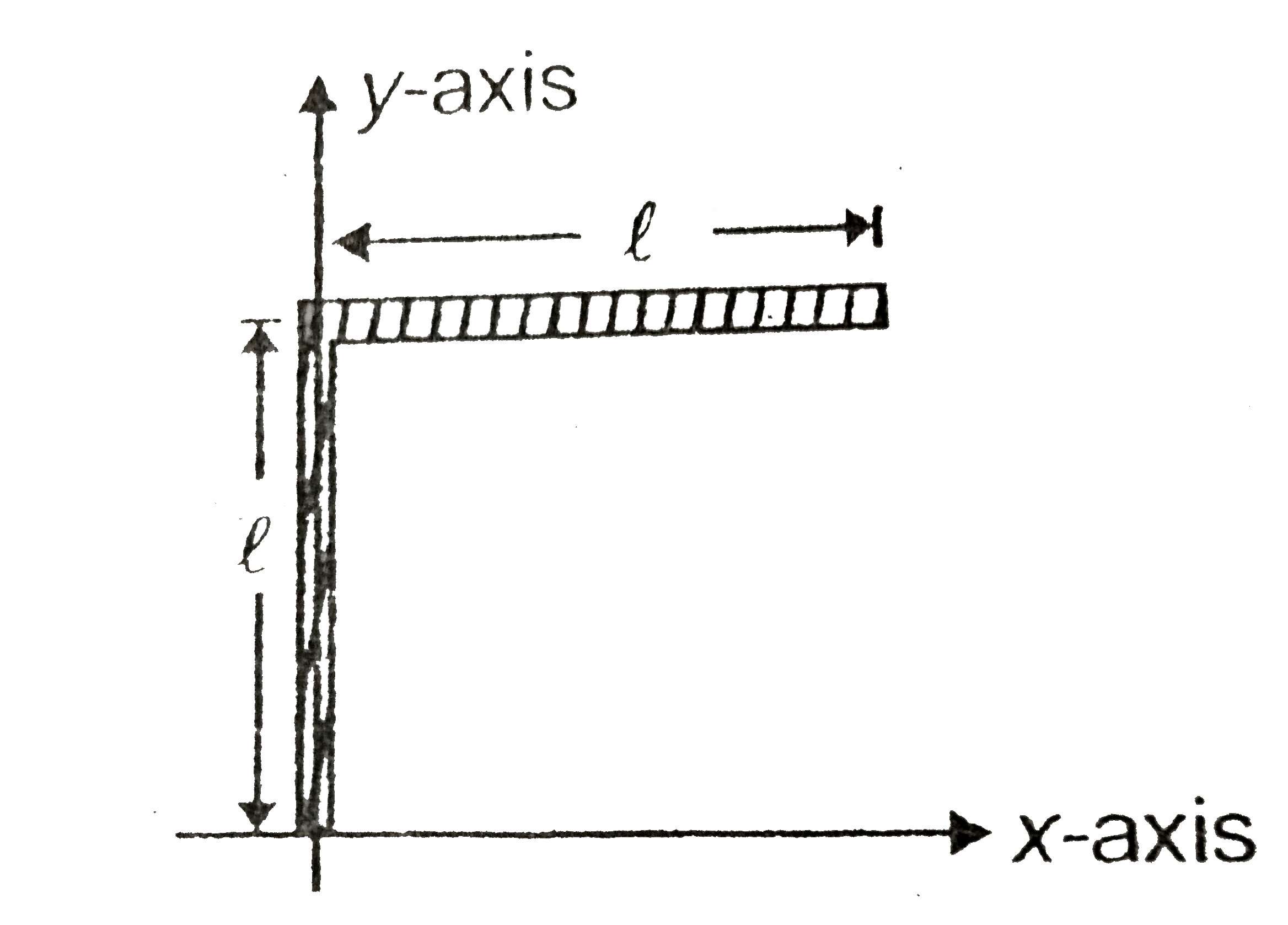
View SolutionTwo particles of equal mass are projected simultaneously with speeds `20 m//s` end `10sqrt(3)m//s` as shown in figure. Find the maximum height reached by the centre of mass of the particles
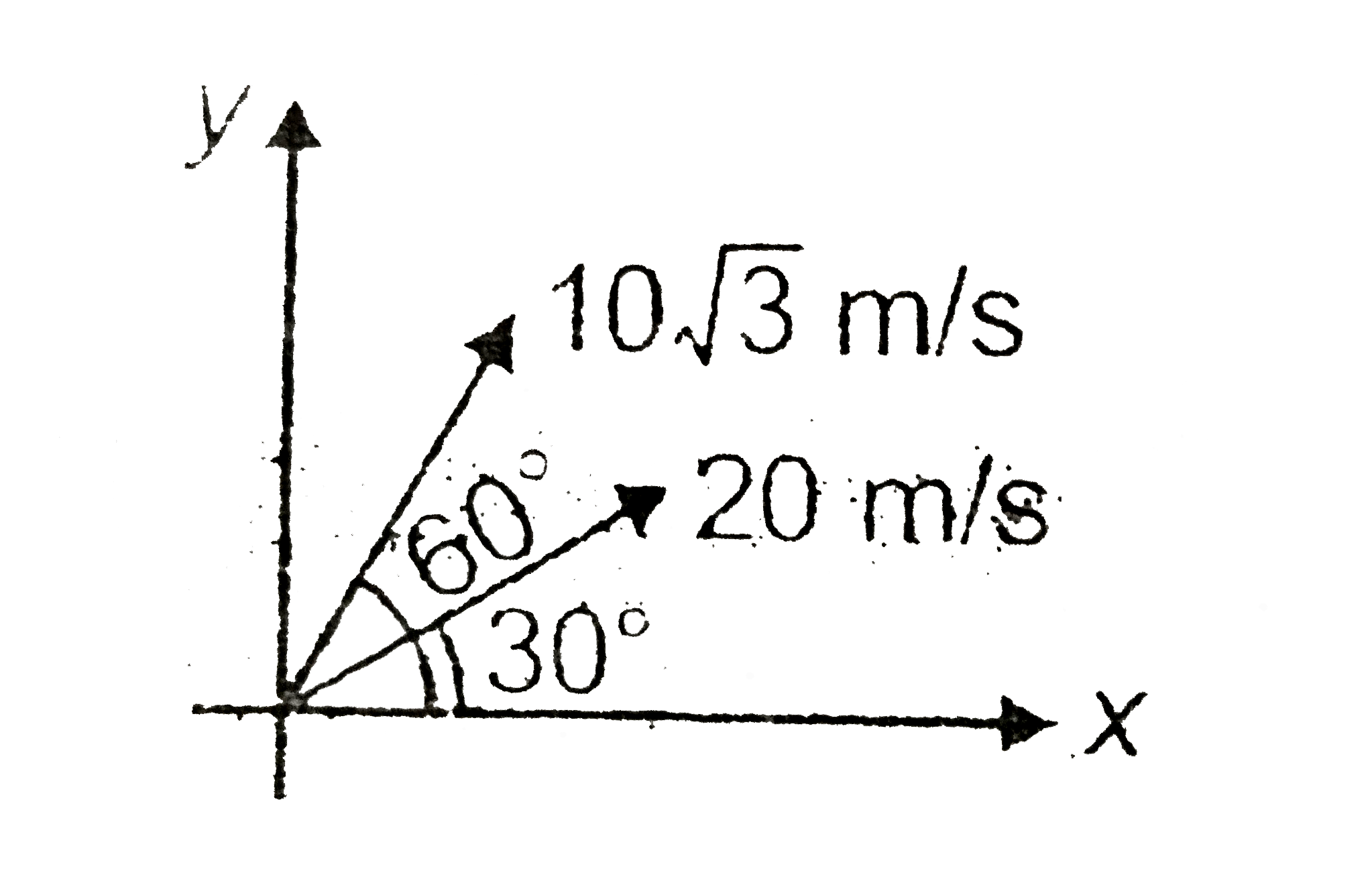
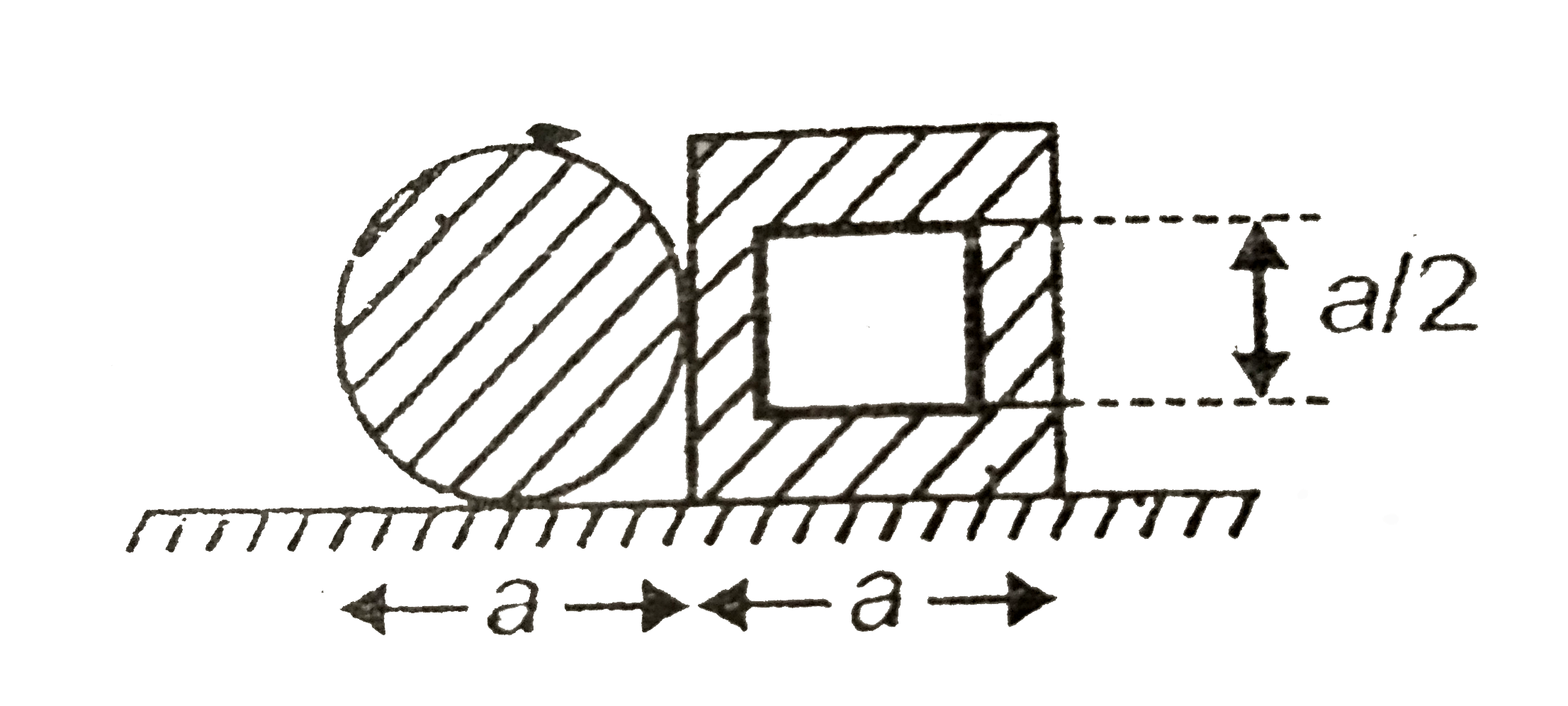
View SolutionA circular plate of diameter `'a'` is kept in contact with a square plate of side a as shown. The density of the material and the thickness are same everywhere. The centre of mass of composite system will be
View SolutionA body of mass `m` is projected from ground for horizontal range `R`. At the highest point it is fragmented into two identical parts. If one parts returns back to the point of projection, then other part will have the horizontal range
View SolutionA man of mass `50 kg` us standing on a `100 kg` plank kept on a fricitonless horizontal floor. Initially both are at rest. If the man starts walking on the plank with speed `6m//s` towards right relative to the plank, then amount of muscle energy spent by the man is
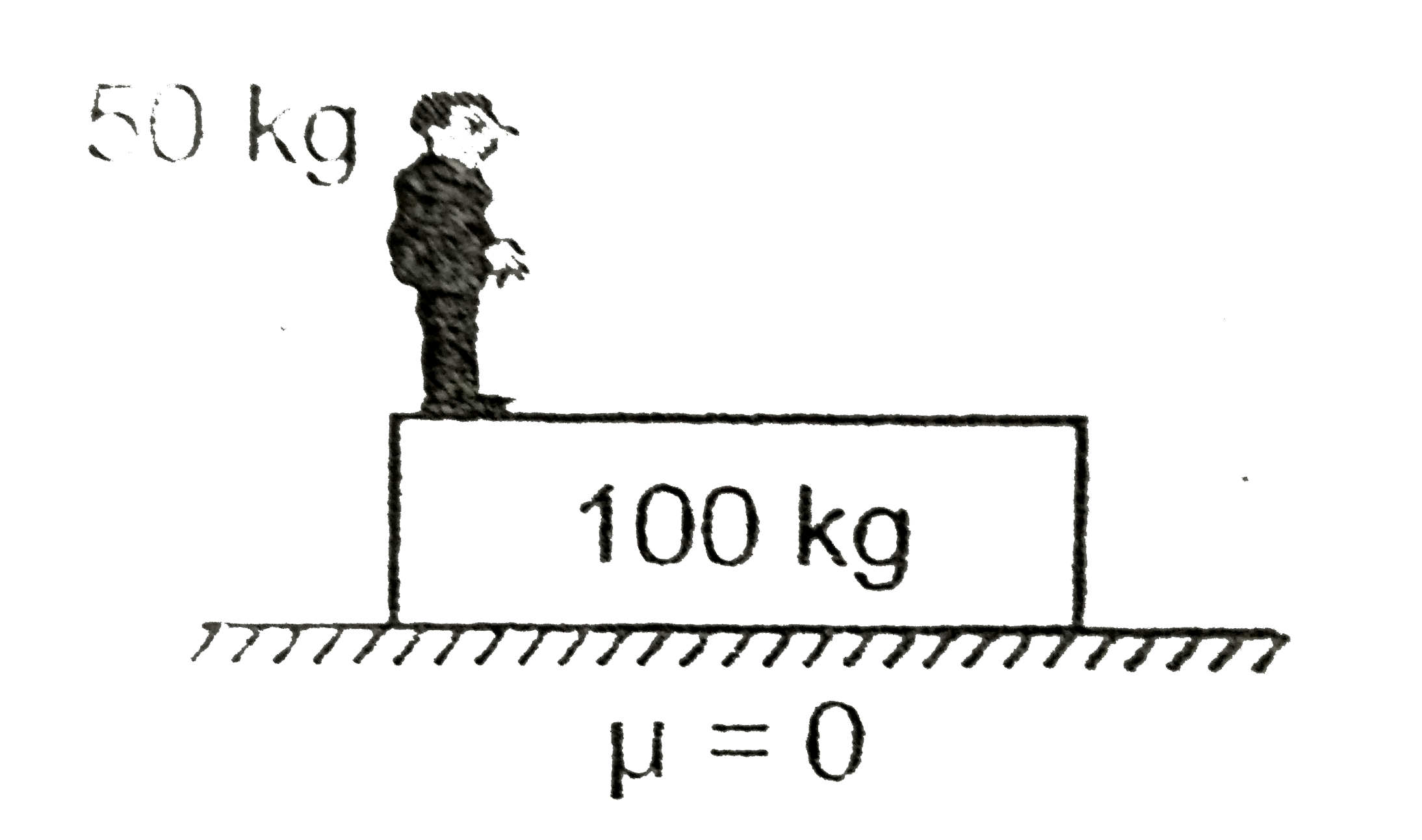
View SolutionA man of mass `m` jumps onto a boat which has a mass `M`. If the person has a horizontal component of velocity `v` relative to boat, just before he enters the boat and the boat is travelling at speed `v_(0)` away from the pier when he makes the jump, the resulting speed of man and boat is
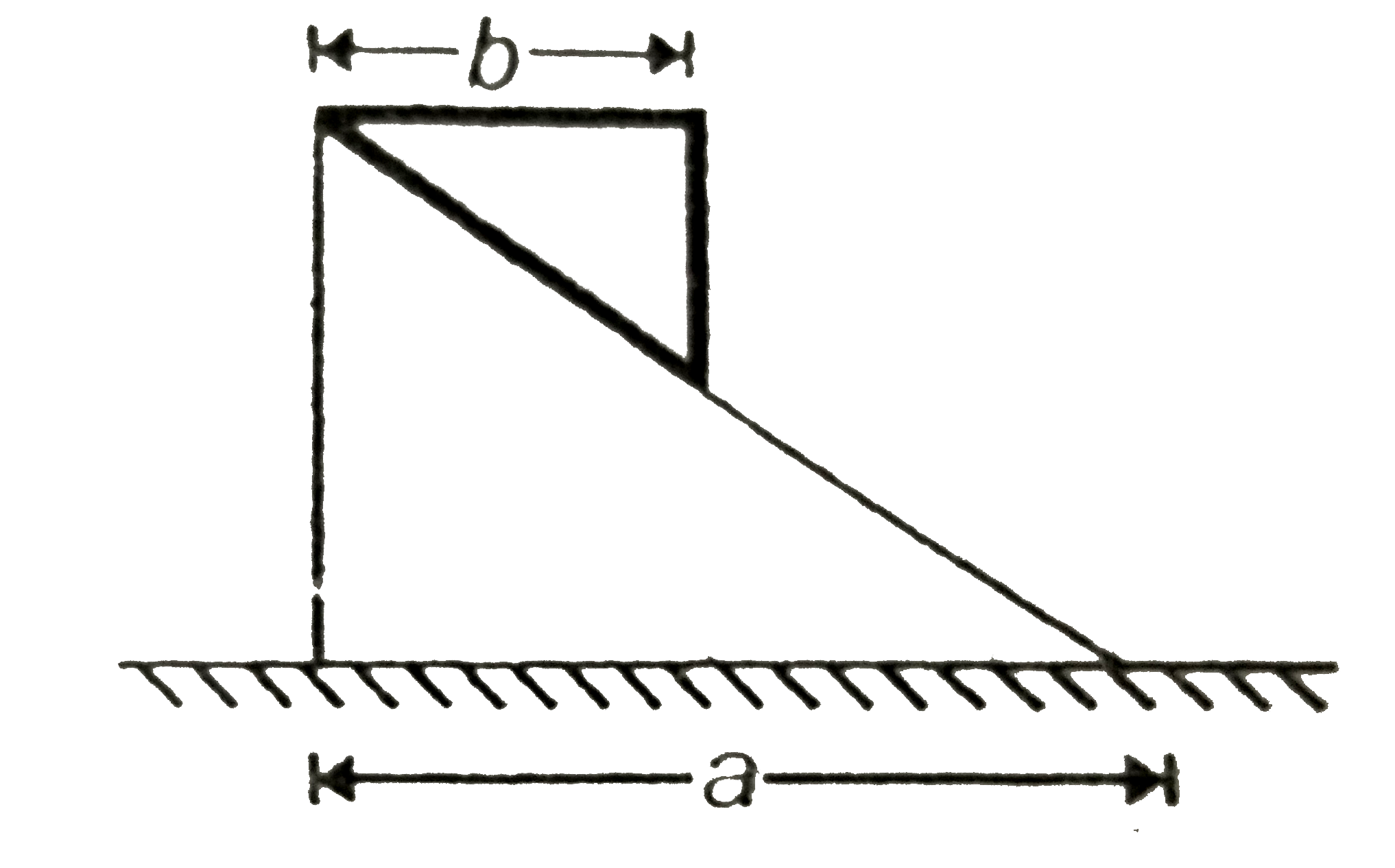
View SolutionTwo smooth prisms of similar right-triangular sections are arranged on a smooth horizontal plane as shown in figure. The lower prism has a mass `eta` times the upper prism. The prisms are held in an initial position as shown and are then released. As the upper prism touches the horizontal plane, the distance moved by the lower prism is
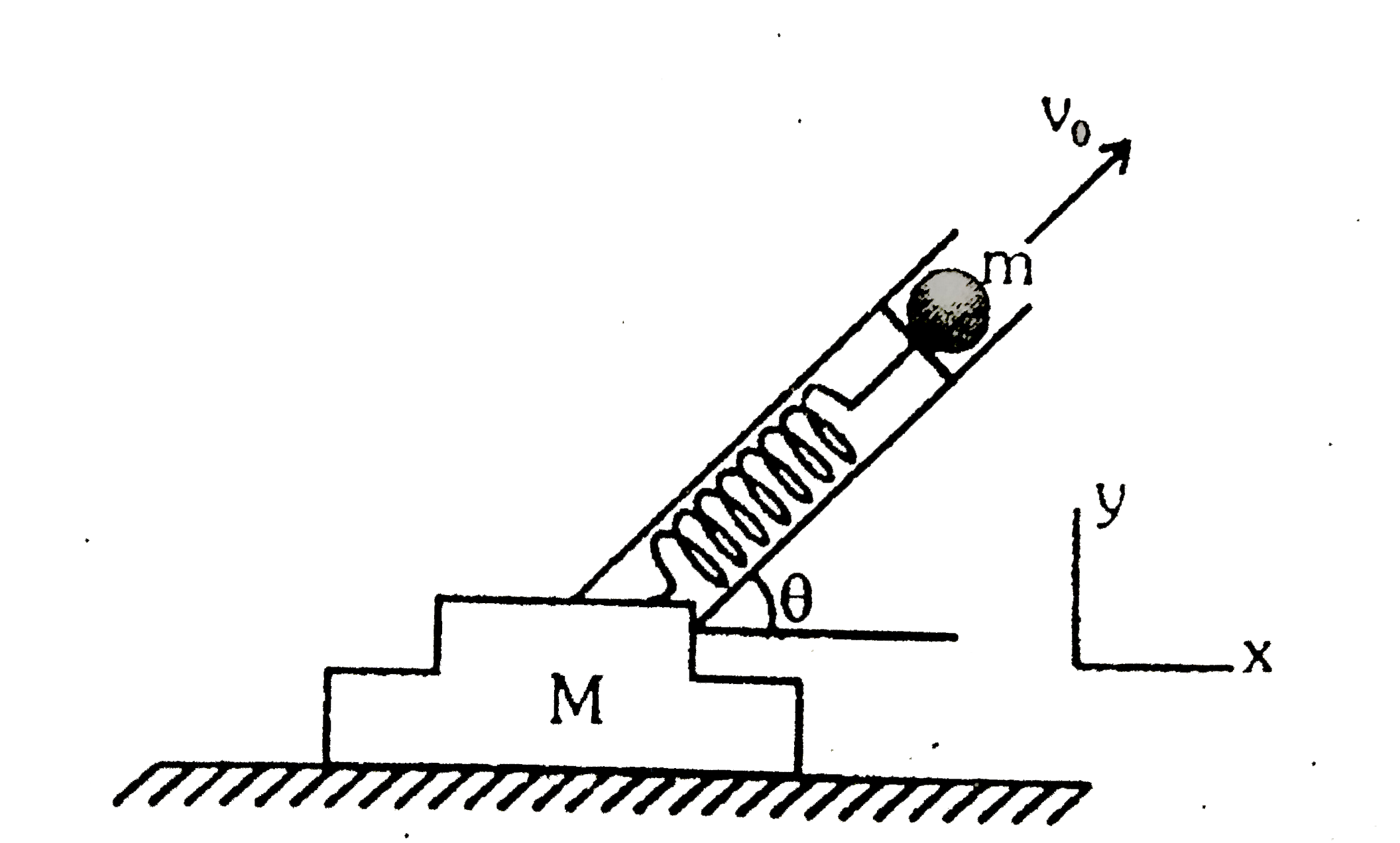
View SolutionSpring Gun Recoil
A loaded spring gun, initially at rest on a horizontal frictionless surface, fires a marble at angle of elevation theta. The mass of the gun is M, the mass of the marble is m, and the muzzle velocity of the marble is `v_0`. What is the final motion of the gun ?
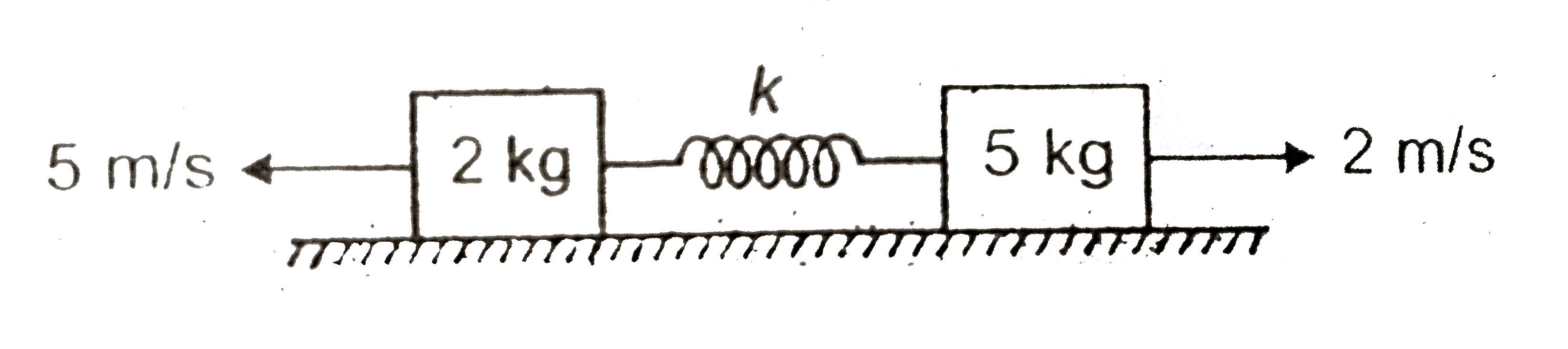
View SolutionTwo blocks of mass `2kg` and `5kg` are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant `35 N/m`. Find the maximum compression in the spring.
View SolutionA ball is allowed to fall from rest on a horizontal floor from a height of `10m`. If there is `20%` loss of energy due to impact, then after one impact ball will go upto
View SolutionA particle is dropped from rest from a height `h_(0)` on a horizontal floor. The coefficient of restitution between the floor and particle is `e`. Maximum height attained by the particle after first rebound is
View SolutionDuring collision between the objects.
View SolutionA particle of mass `m` moving with a speed `u` strikes a smooth horizontal surface at an angle `45^(@)`. The particle rebounds at an angle `phi` with speed `v`. If coefficient of restituion is `(1)/(sqrt(3))`, then angle `phi` is
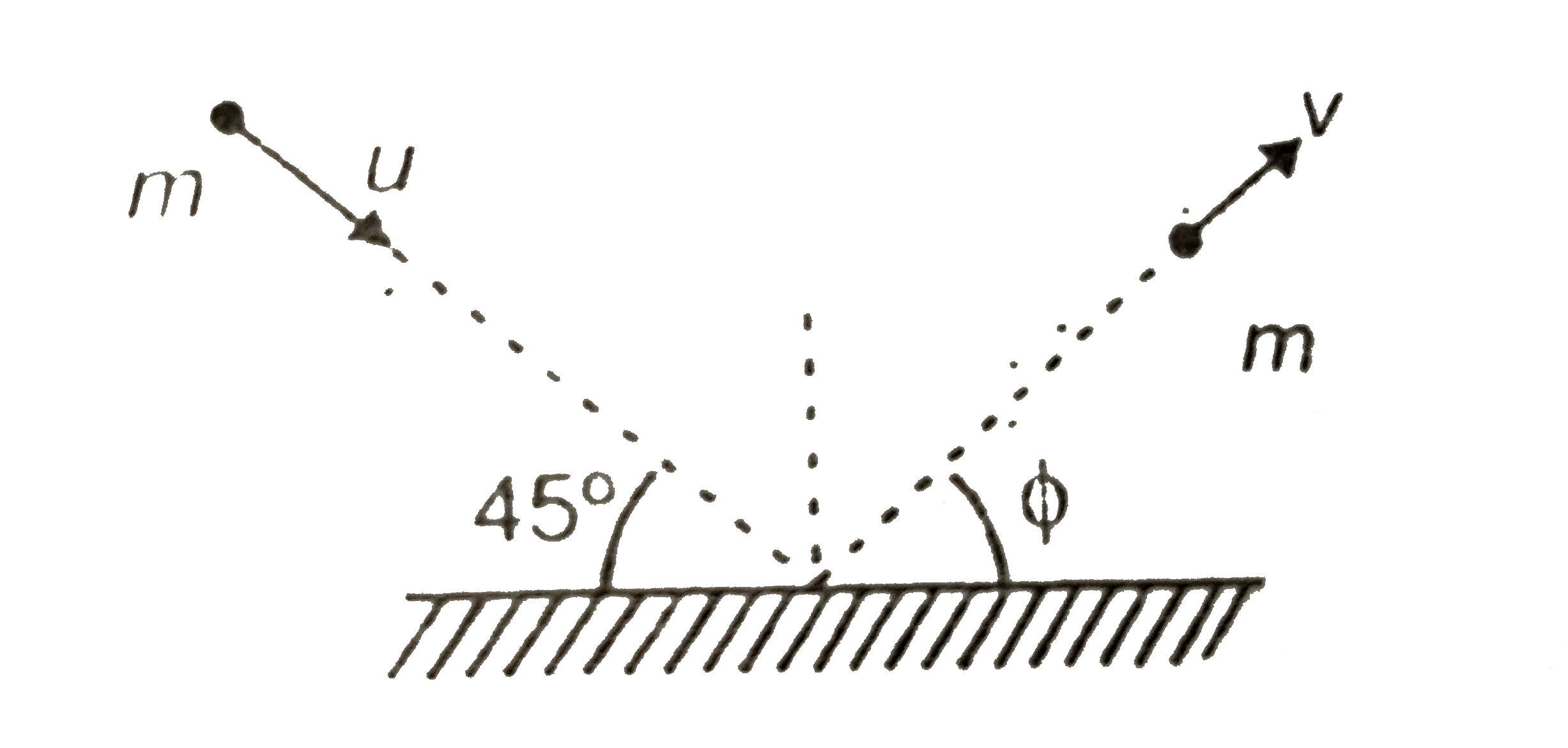
View SolutionA particle collides with a smooth, surface with speed `u` at an angle `theta`. Coefficient of restitution is `e`. Find the ratio of the horizontal ranges of two consecutive projectile motions
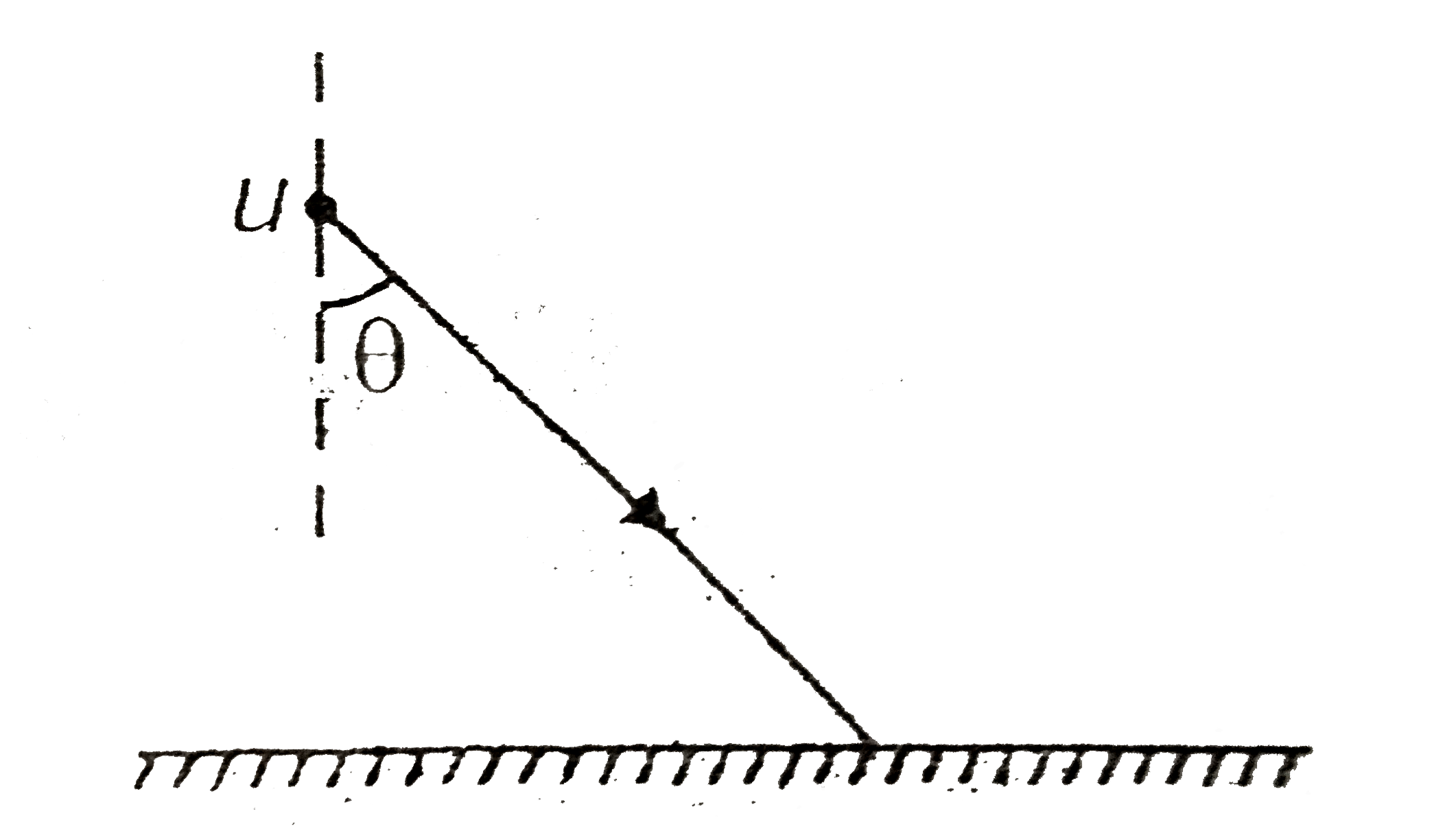
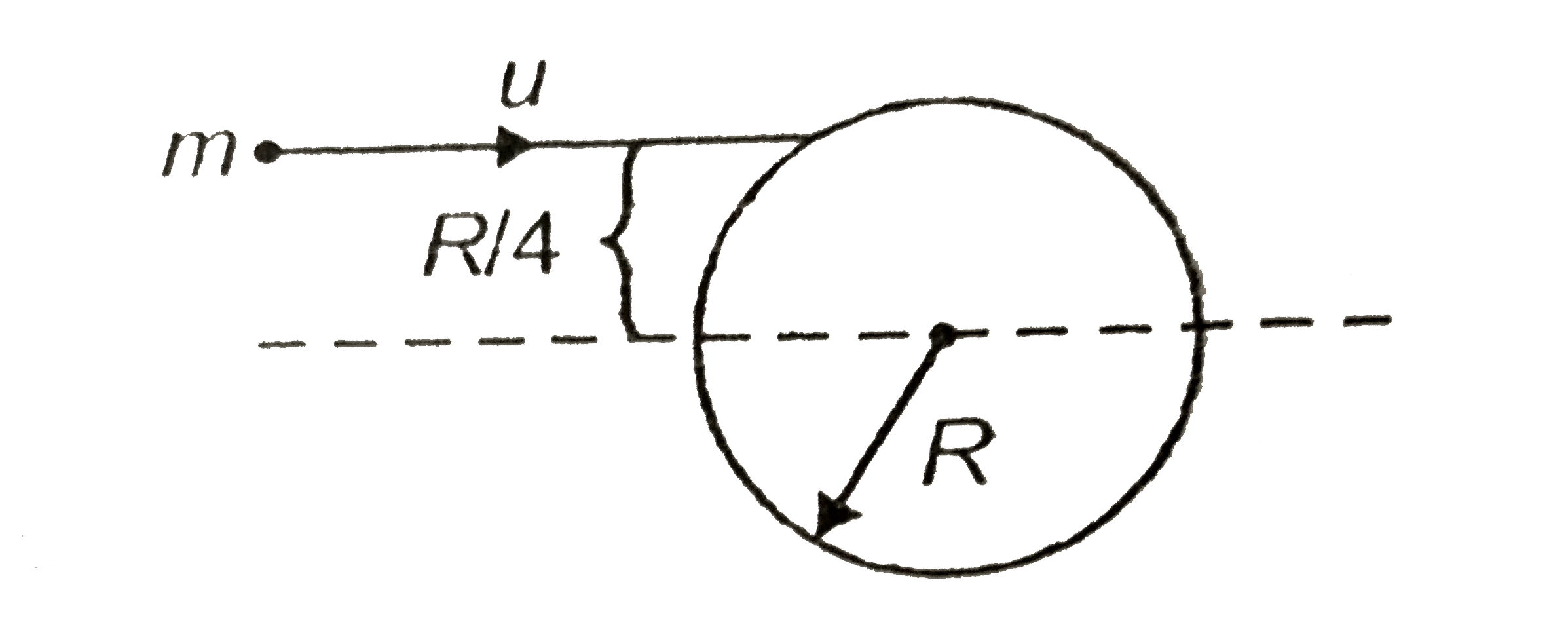
View SolutionA particle of mass `m` strikes a disc of radius `R` and mass `m` with a speed `u` as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
View SolutionTwo identical billiard balls are in contact on a table. A third identical ball strikes them symmetrically and comes to rest after impact. The coefficient of restitution is :
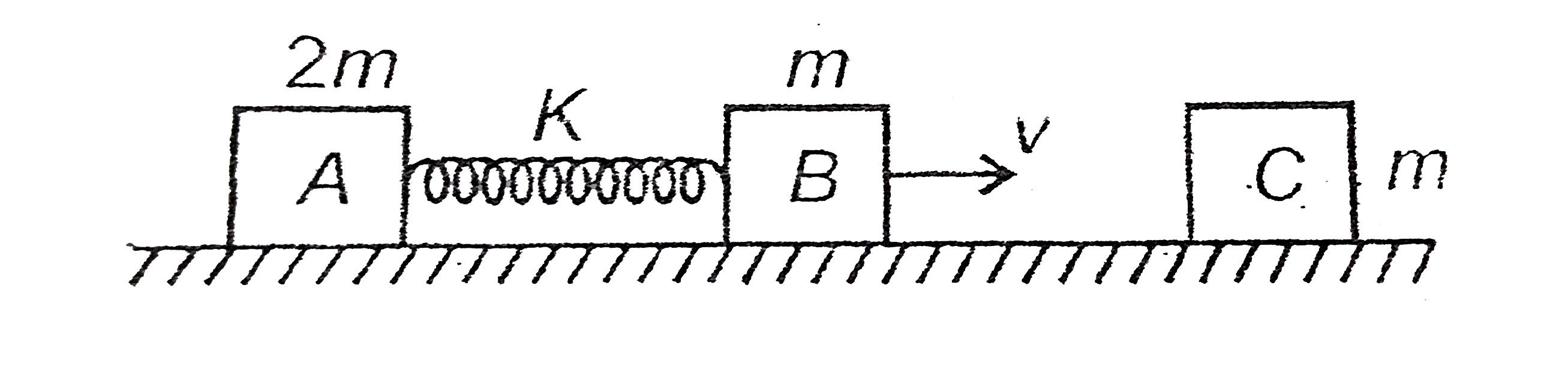
View SolutionTwo blocks `A` and `B` of mass `2m` and `m` respectively are connected to a massless spring of force constant `K` as shown in figure `A` and `B` are moving on the horizontal frcitionless surface with velocity `v` to right with underformed spring. If `B` collides with `C` elastically, then maximum compression of the spring will be
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA body of mass `m` moving with a velocity `v` is approaching a second object of same mass but at rest. The kinetic energy of the two objects as viewed from the centre of mass is
View SolutionA body of mass `M` is moving on a smooth surface with speed `v_(0)`. Another body of same mass `M` attached to a spring is kept on the same surface as shown. The moving mas makes an impact with the spring of spring constant `k` and starts compressing it. What is the maximum compression in the spring ?

View SolutionA rigid rod is rotating as well as translating on a smooth horizontal surface. The velocities of its ends at any moment are as shown in figure. If `theta=60^(@)` find the value of `v_(2)`
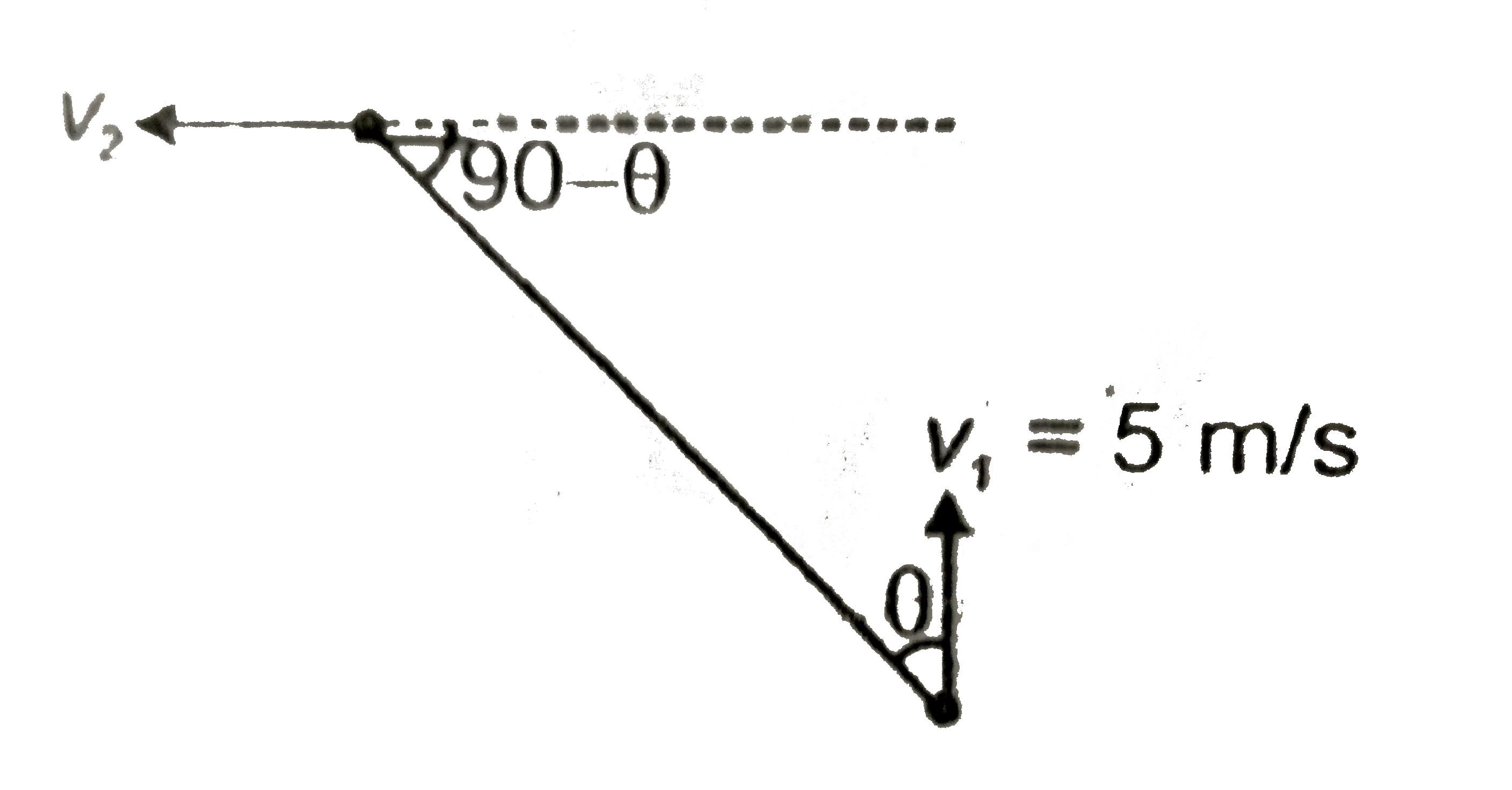
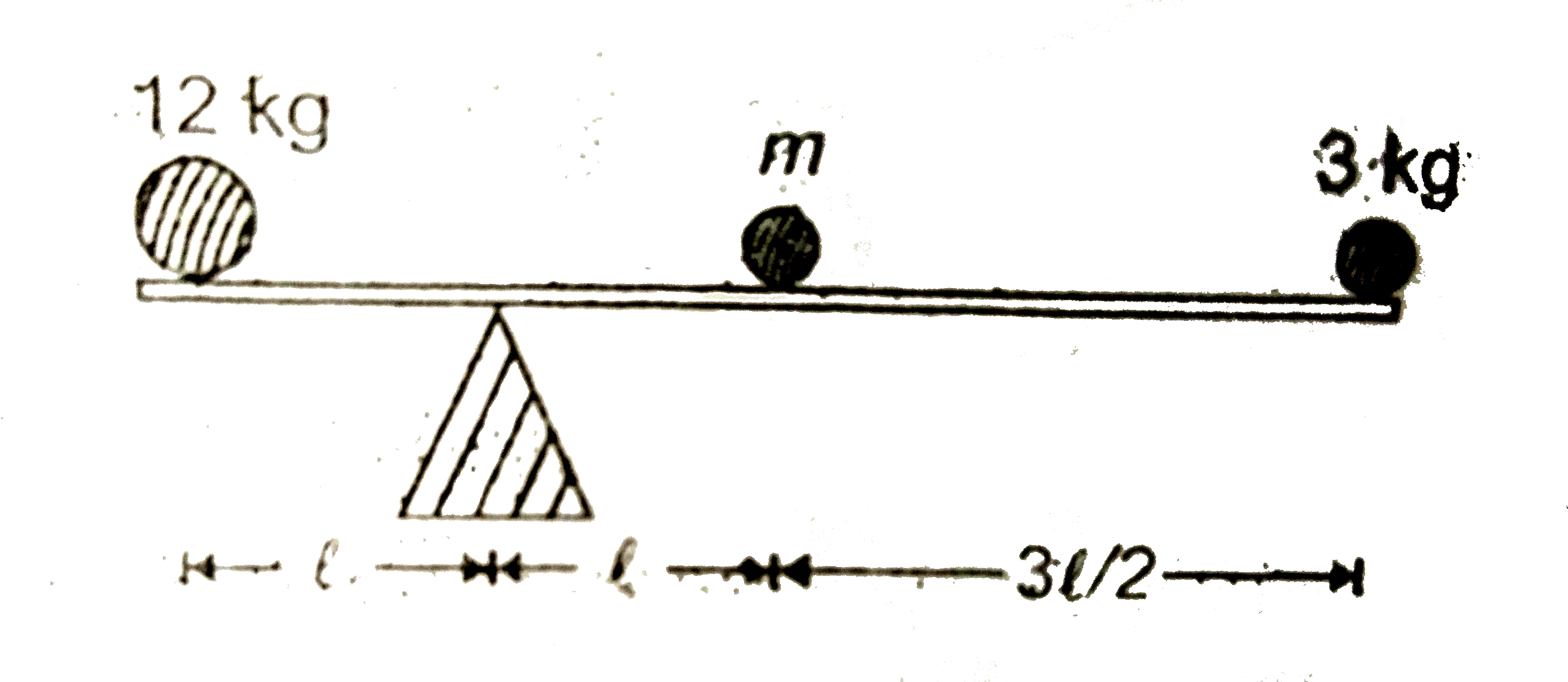
View SolutionFor the equilibrium of the system shown, the value of mass `m` should be
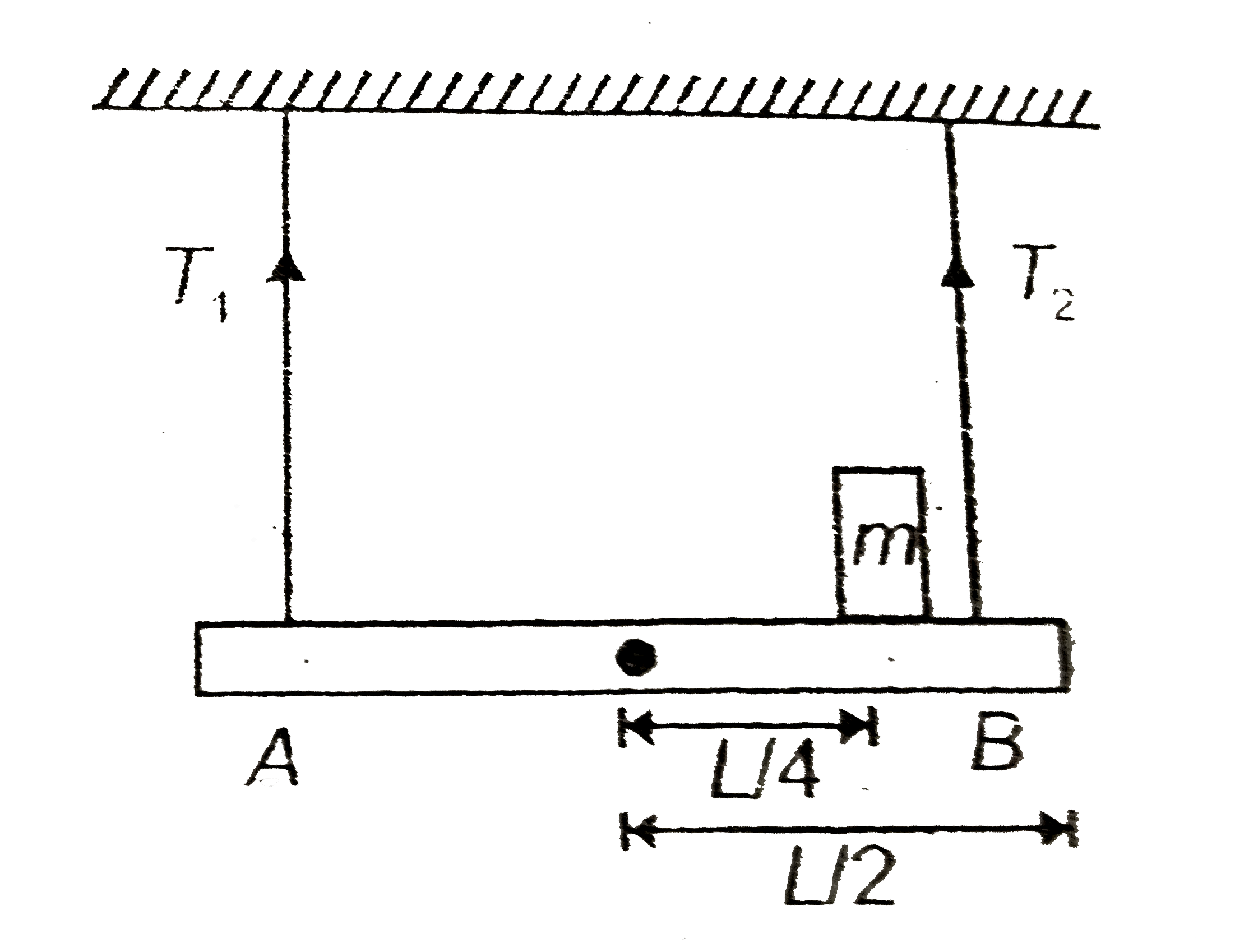
View SolutionA rod `AB` of mass `m` is hung by two ideal threads. Find the ratio of tensions in the two threads `((T_(1))/(T_(2)))`.
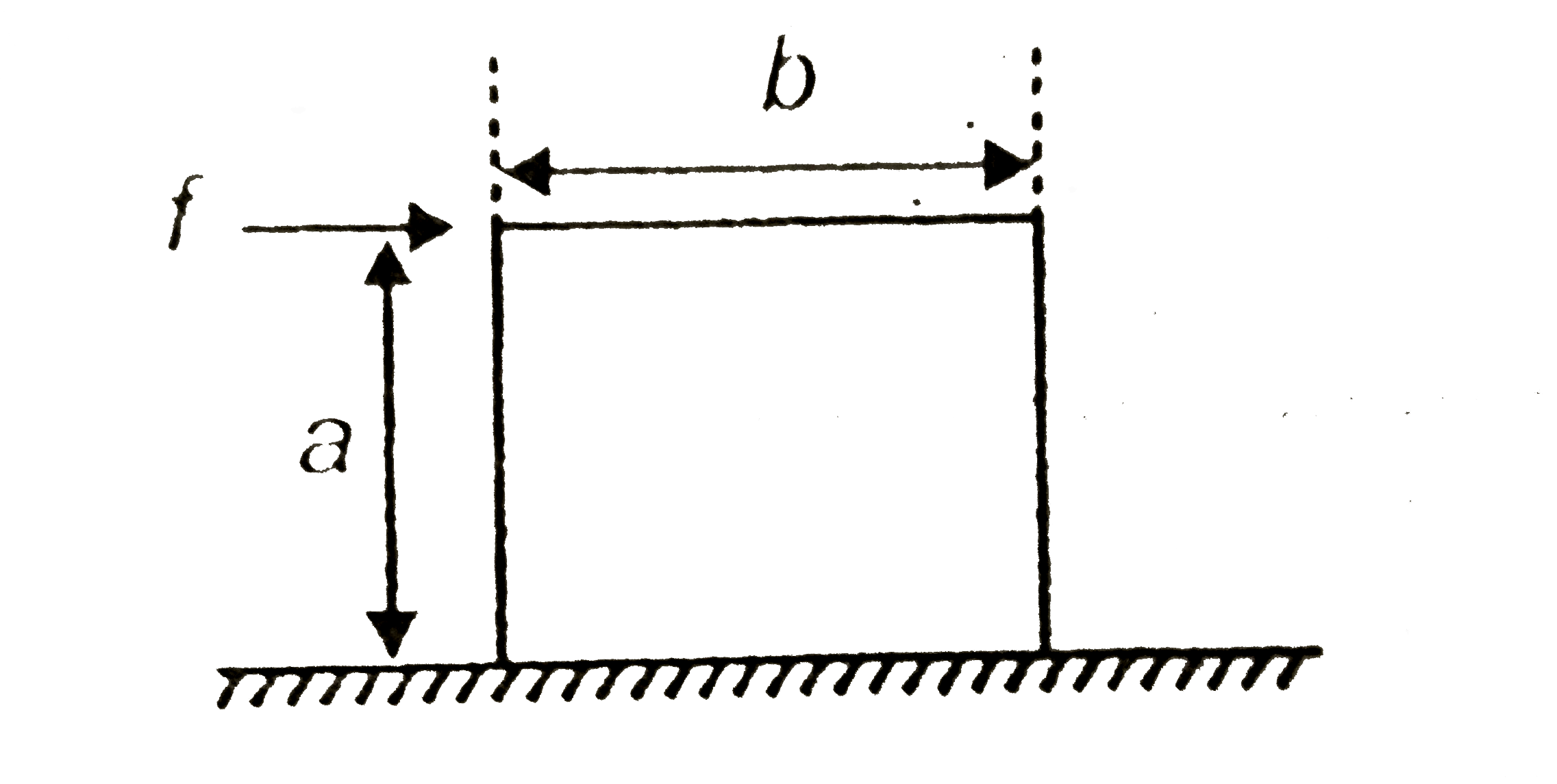
View SolutionA cubical block of height `a` and width `b` is placed on the horizontal surface with sufficient fricition. For a given force.
View SolutionA uniform solid cylinder having height `l` and diameter `d` is placed on a rough horizontally plank which is being pulled horizontal with an acceleration. Find the maximum value of the acceleration for which the cylinder remain in equilibrium
View SolutionThe moment of inertia of a flat angular ring is having mass `M`, inner radius a and outer radius `b` about the perpendicular axis through the centre is
View SolutionMoment of inertia of a thin semicircular disc `(mass - M & radius = R)` about an axis through point `O` and perpendicular to plane of disc, is given by :
 .
.
View SolutionFour rods of equal mass `m` and length `L`. Forms a square `ABCD` as shown in figure. The moment of inertia of `ABCD` about the axis `OO'` passing through the point `A` is
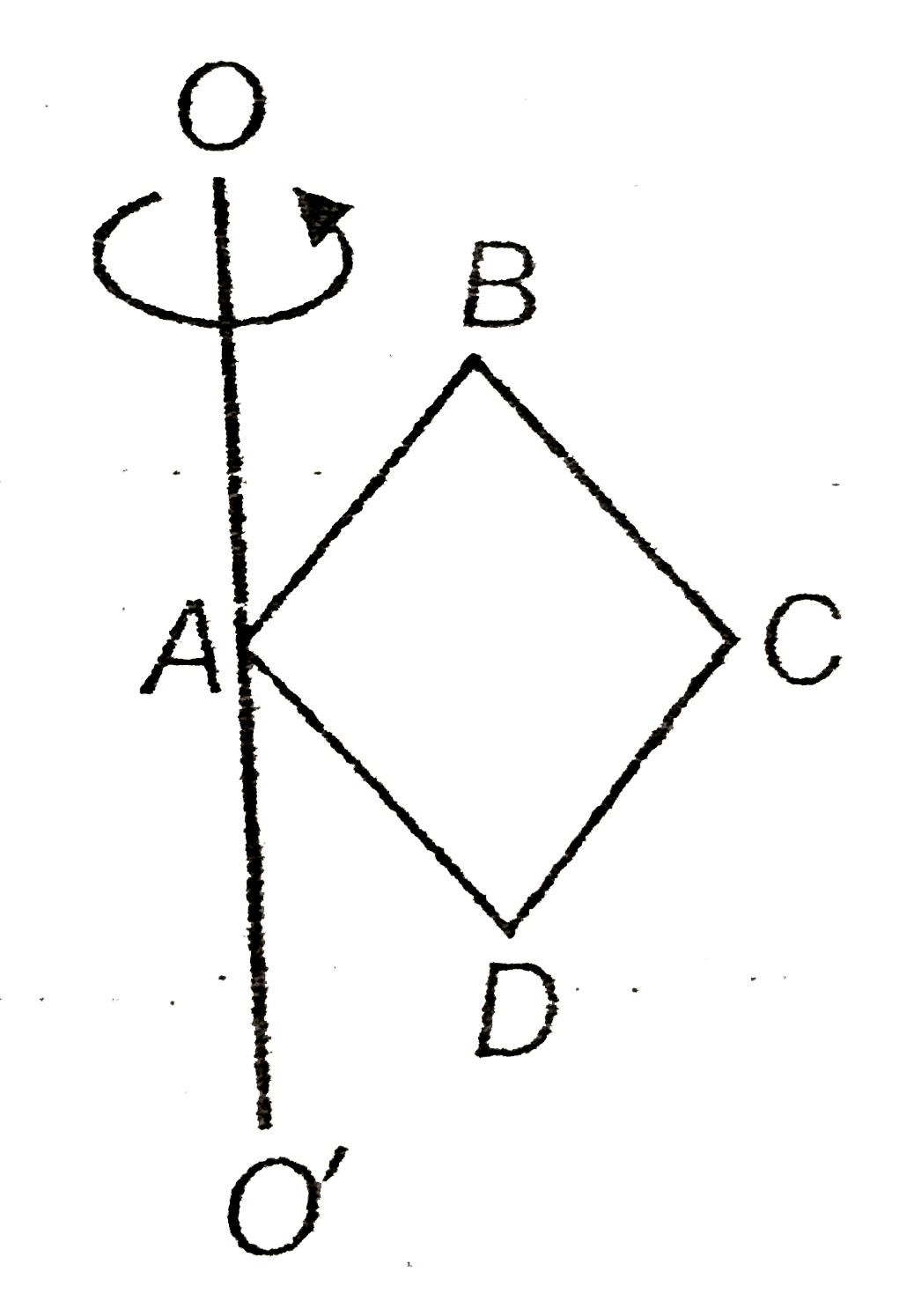
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance `x` from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is `R`. The value of `x` is
View SolutionTwo spheres each of mass `M` and radius `R//2` are connected with a massless rod of length `R`. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionMoment of inertia of a half ring of mass `m` and radius `R` about an axis passing through point `A` perpendicular to the plane of the paper is `I_(A)`. If `I_(C )` is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point `C`, then
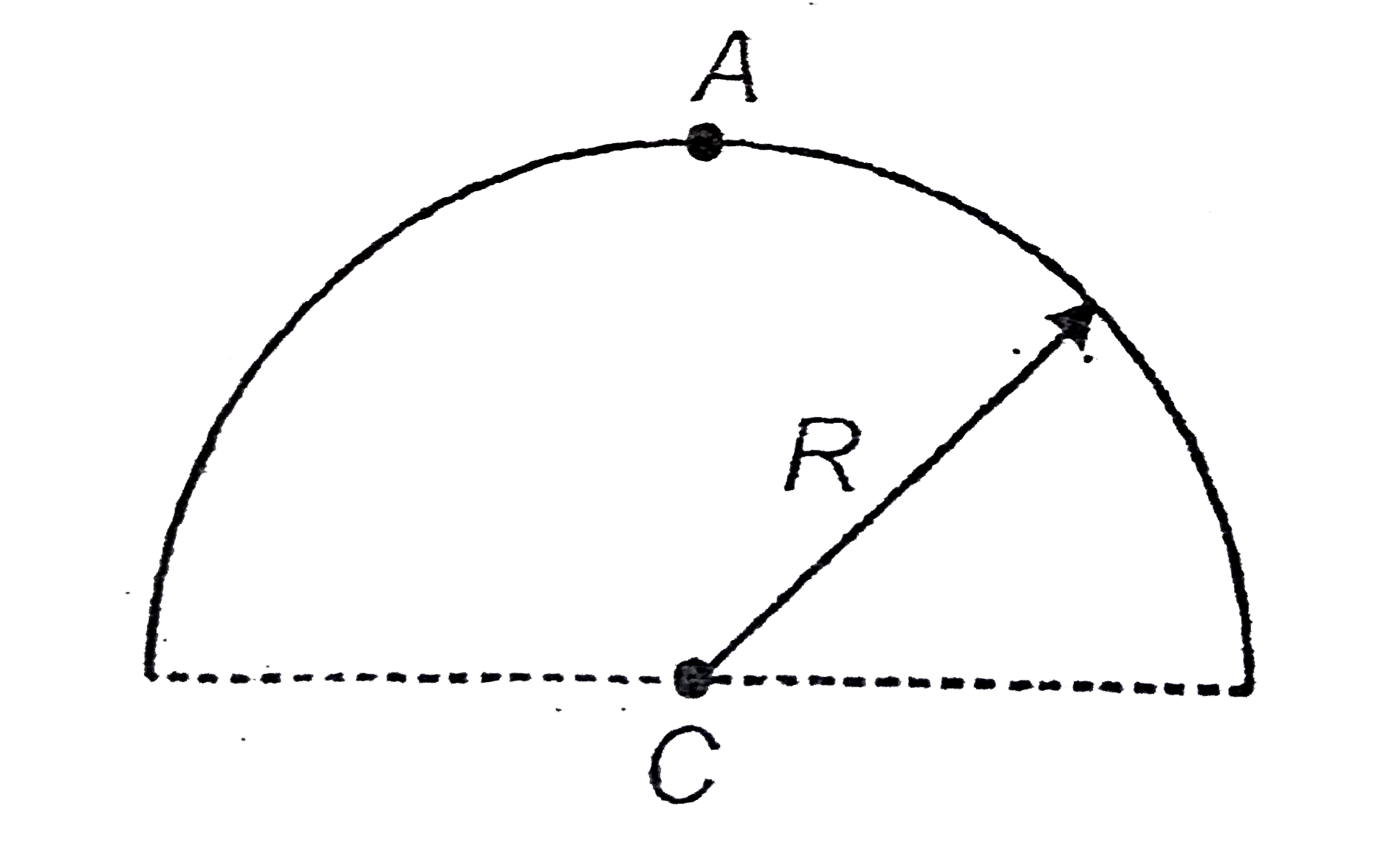
View SolutionFrom a uniform sphere of mass `M` and radius `R` a cavity of diameter `R` is created as shown. Find the ratio of moment of inertia of the sphere left about `"AA"'` and `BB'`.
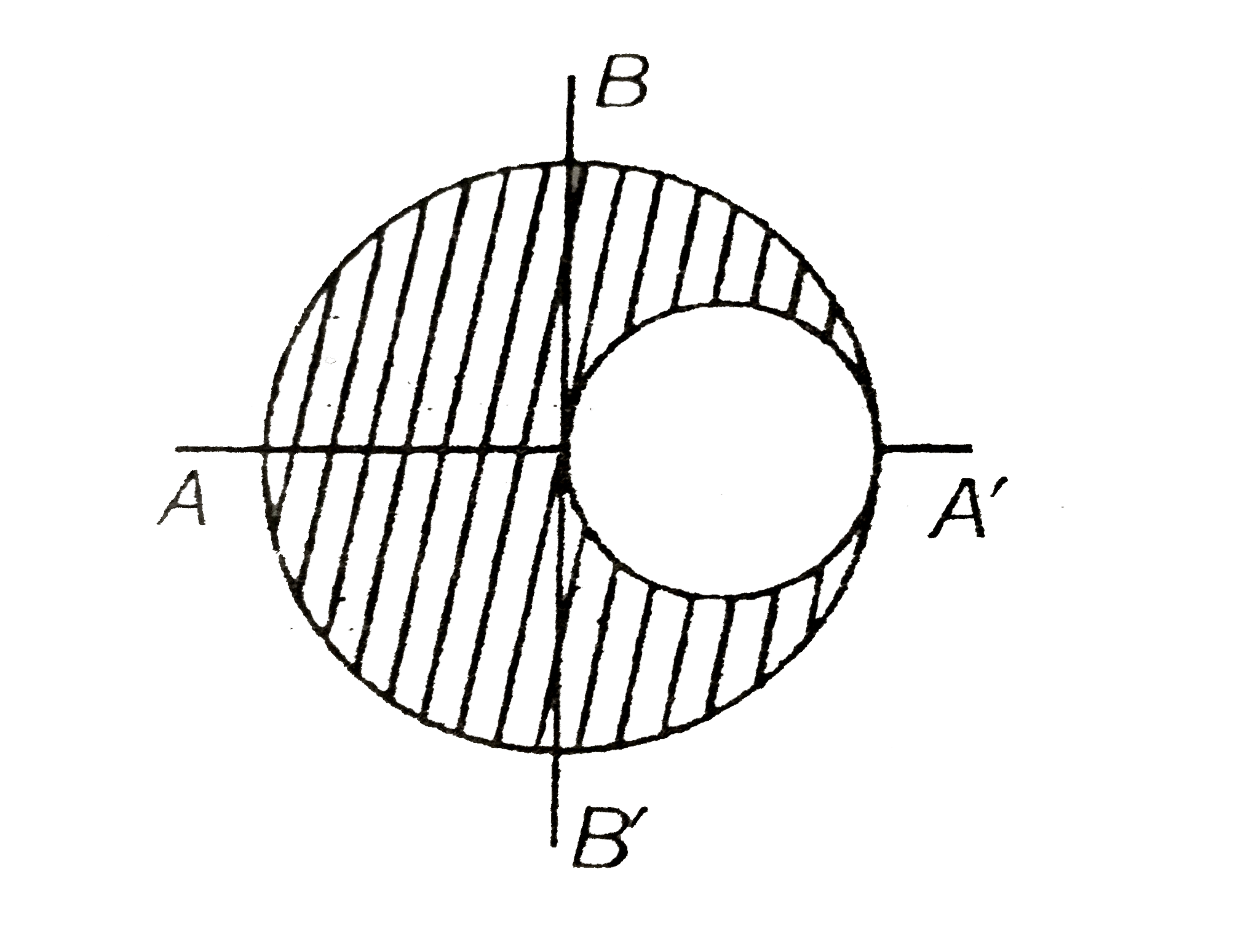
View SolutionThe ratio of the radii of gyration of a spherical shell and solid sphere of the same mass and radius about a tangential axis is
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed `v_(0)`. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View SolutionA disc of radius `R` and mass `M` is under pure rolling under the action of a force `F` applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionA ring of mass `m` and radius `R` is acted upon by a force `F` as shown in the figure. There os sufficient friction between the ring and the ground. The force of friciton force necessary for pure rolling is
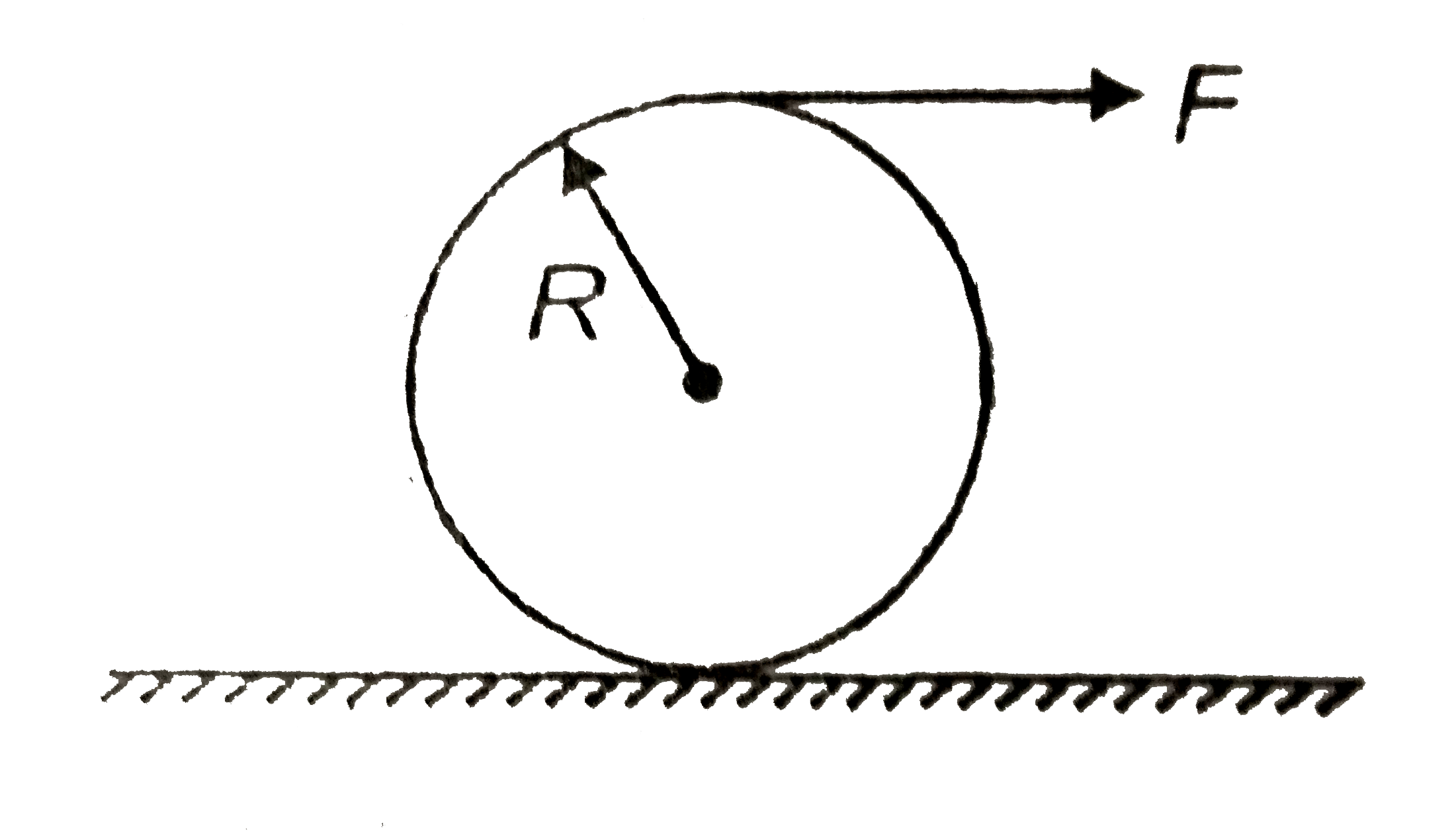
View SolutionA solid sphere of mass `2kg` is pulled by a constant force acting at its centre on a rough surface having co-efficient of friciton `0.5`. The maximum value of `F` so that the sphere rolls without slipping is

View SolutionA hollow sphere is rolling without slipping on a rough surface. The ratio of translational kinetic energy to rotational kinetic energy is
View SolutionA cylinder is released from the top of an incline making angle `theta=45^(@)` with the horizontal. The length of the incline is `2.82m` and mass of cylinder is `1kg`. The coefficient of friciton is `0.2` between the cylinder and the incline. When the cylinder reaches the bottom of the incline, its total kinetic energy is `(g=10m//s^(2))`
View SolutionA hollow spherical ball rolls down on a parabolic path `AB` from a height `'h'` as shown in the figure. Path `AB` is rough enough to prevent slipping of ball and path `BC` is frictionless. The height to which the ball will climb in `BC` is

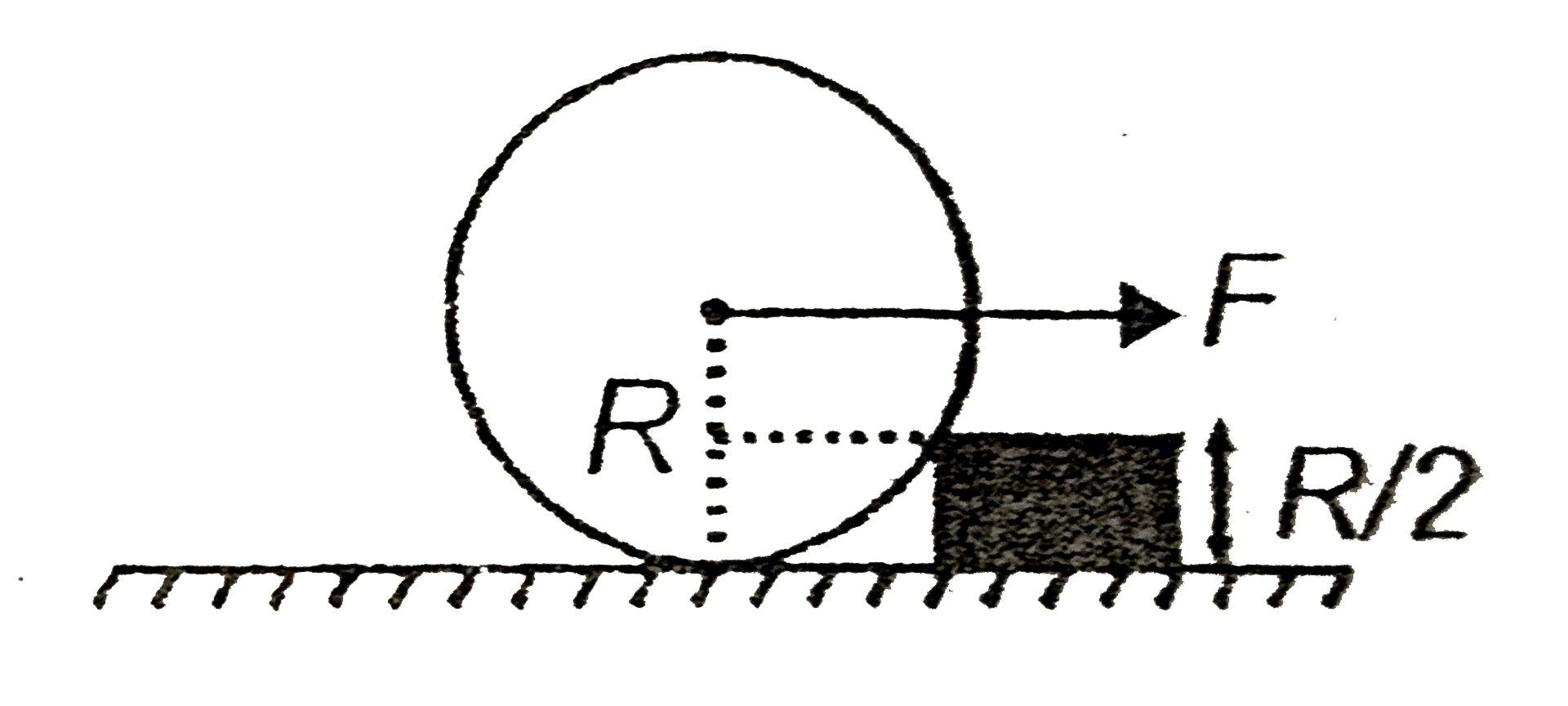
View SolutionThe minimum horizontal force applied to the centre of wheel of radius `R` and weight `w` to pull it over a step of height `R//2`
View SolutionA solid cylinder is rolling without slipping with velocity of its centre of mass `v` and angular velocity about its centre of mass `omega` on a horizontal frictionless surface as shown in figure. If it collides with a frictionless vertical wall `X`, then after collision its velocity and angular velocity respectively become
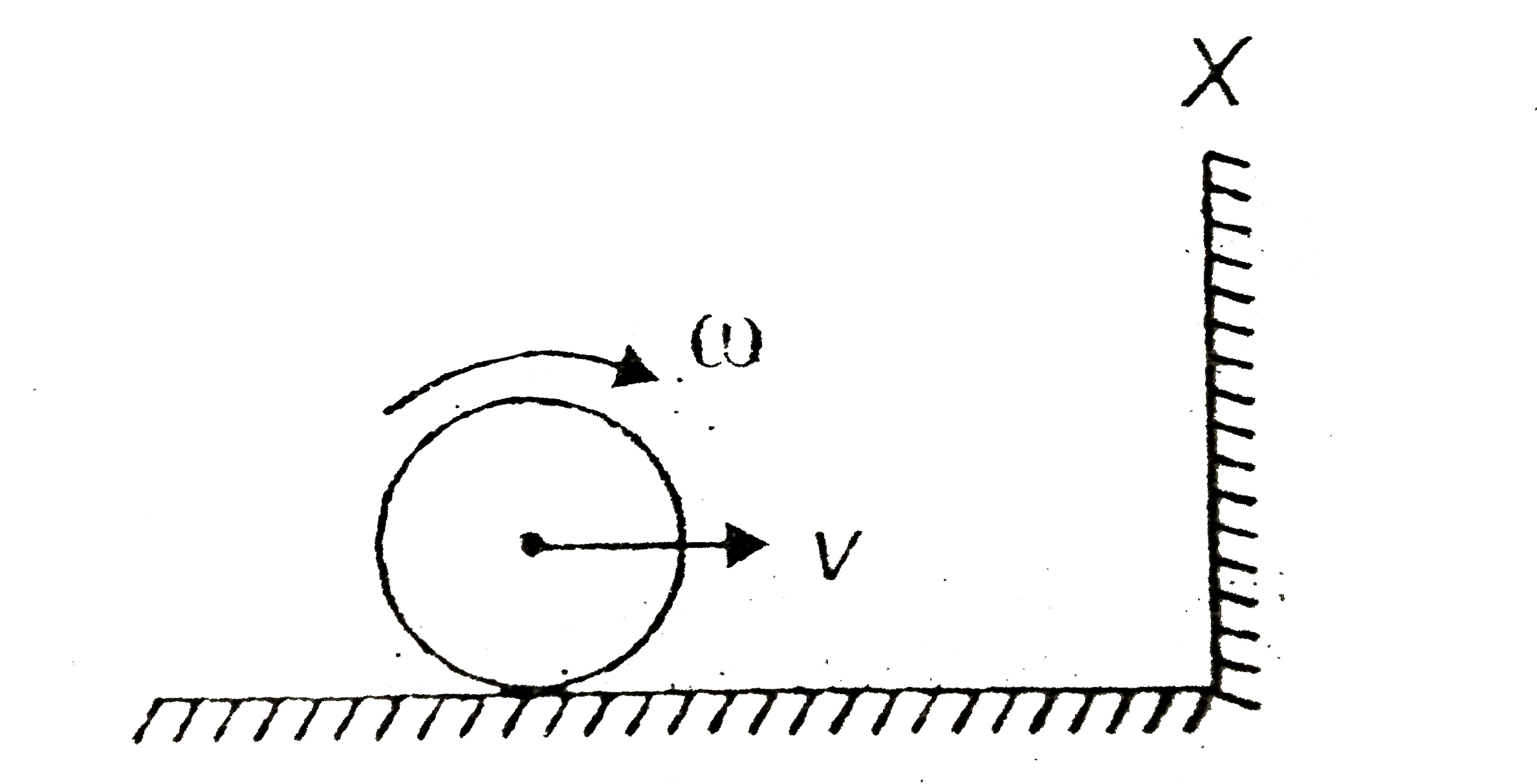
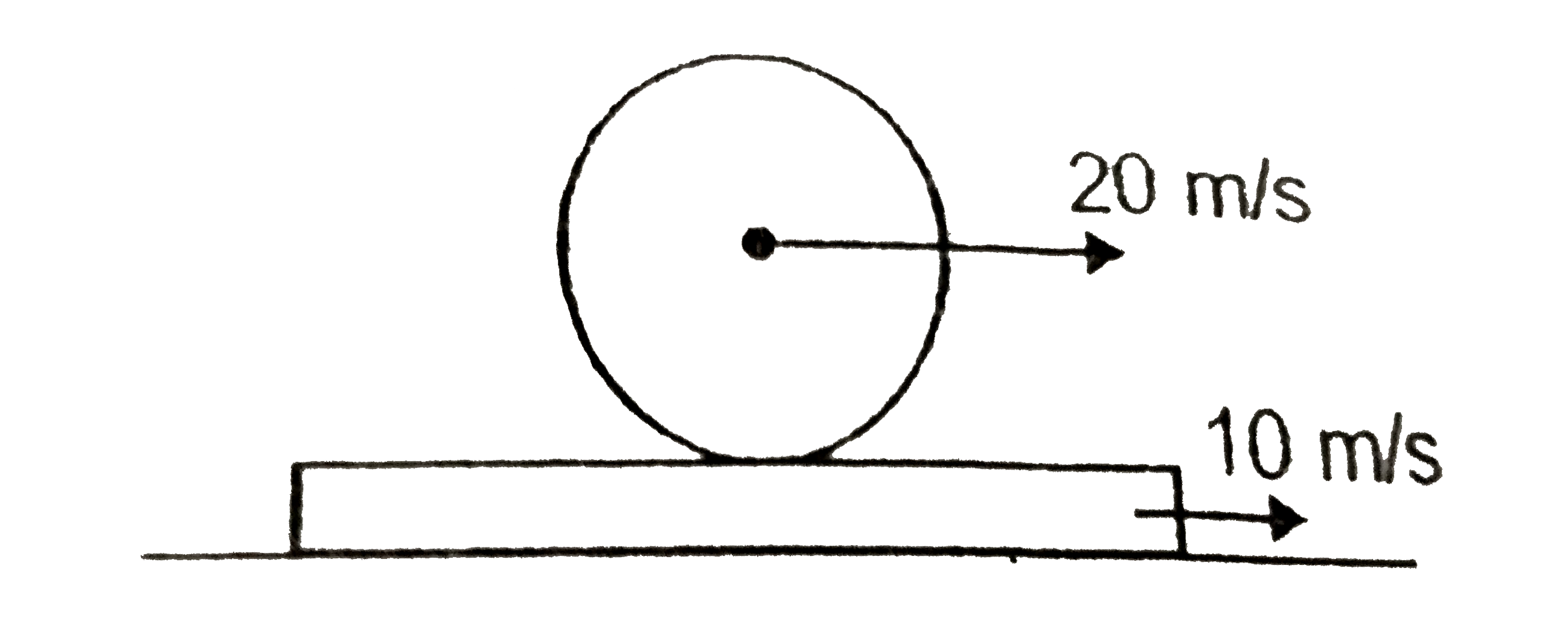
View SolutionA cylinder is rolling without slipping on a plank which is also moving with speed `10m//s` on a horizontal surface as shown. The speed of centre of the cylinder is `20m//s`. The mass of cylinder is `2kg`. The kinetic energy of the cylinder when observed from ground is
View SolutionThree identical rods `A`, `B` and `C` each having length `l` are in shape of letter `H` as shown in the figure and free to move in vertical plane. Find he velocity of `A` at the lowest position when the system is disturbed slightly

View SolutionA particle of mass `m=3kg` is projected at an angle of `45^(@)` with the horizontal with a speed of `20sqrt(2)m//s`. The angular momentum of the particle at the highest point of trajectory about a horizontal axis passing through the origin and perpendicular to the plane of motion is
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with an angular speed `omega`. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become
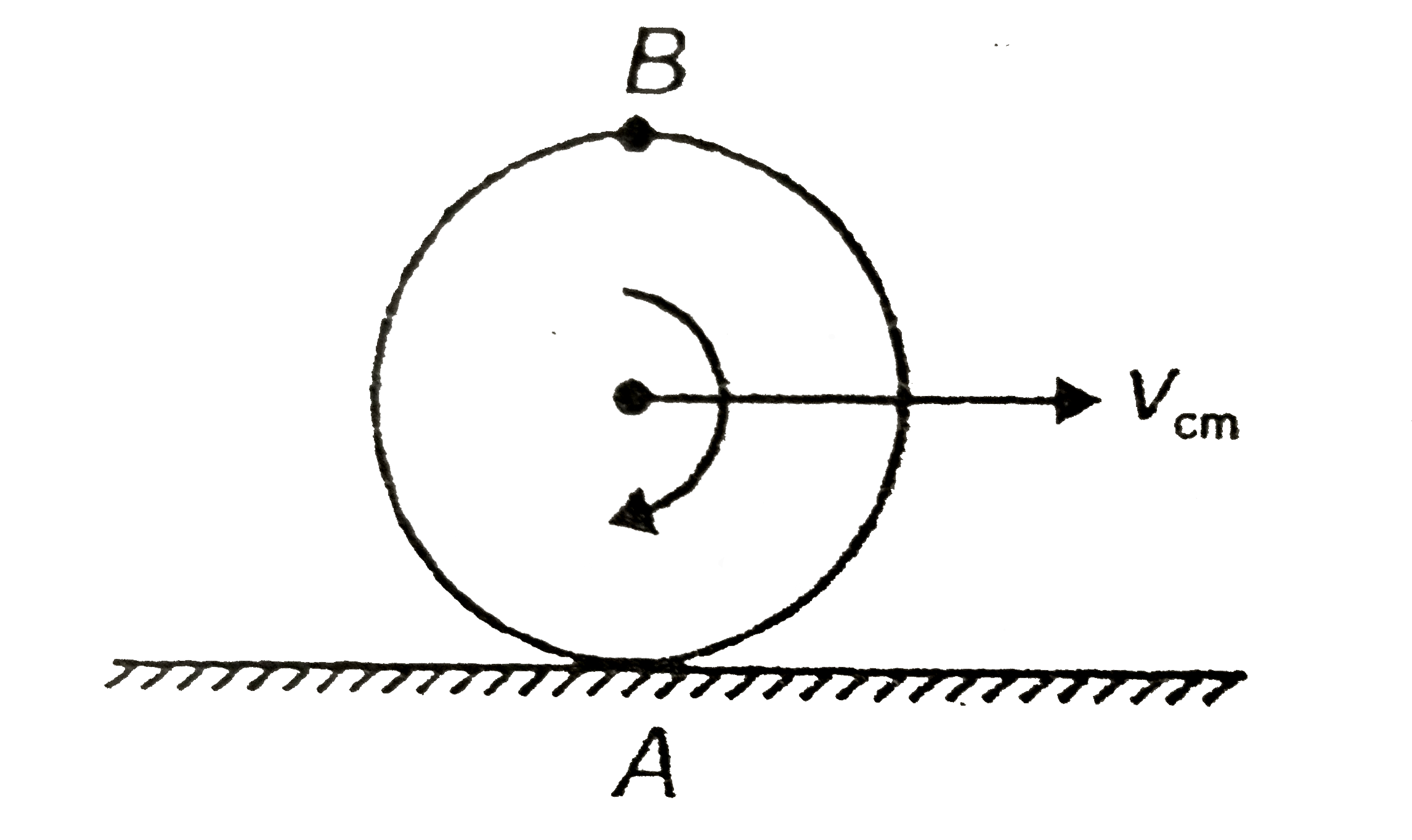
View SolutionA disc is undergoing rolling on a horizontal surface. Which of the statement about angular momentum of the disc is incorrect ?
View SolutionA theif is running with speed of `10m//s` along the line `y=10m`. The `x-y` plane is horizontal. A searchlight kept at the origin is always aimed at the theif. To do so its has to be continuosly rotated with some angular speed `omgea`. When the line joining the thief with origin is making an angle `theta=45^(@)` with the `y` axis, the value of `omega` is
View SolutionA rod `AB` of mass `m` and length `L` is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is `omega`. The force applied on the rod by the pivot is
View SolutionA uniform rod of mass `M` and length `L` is standing vertically along the `y`-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View SolutionA rod of mass `m` and length `l` hinged at the centre is placed on a horizontal surface. A bullet of mass `m` moving with velocity `v` strikes the end A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
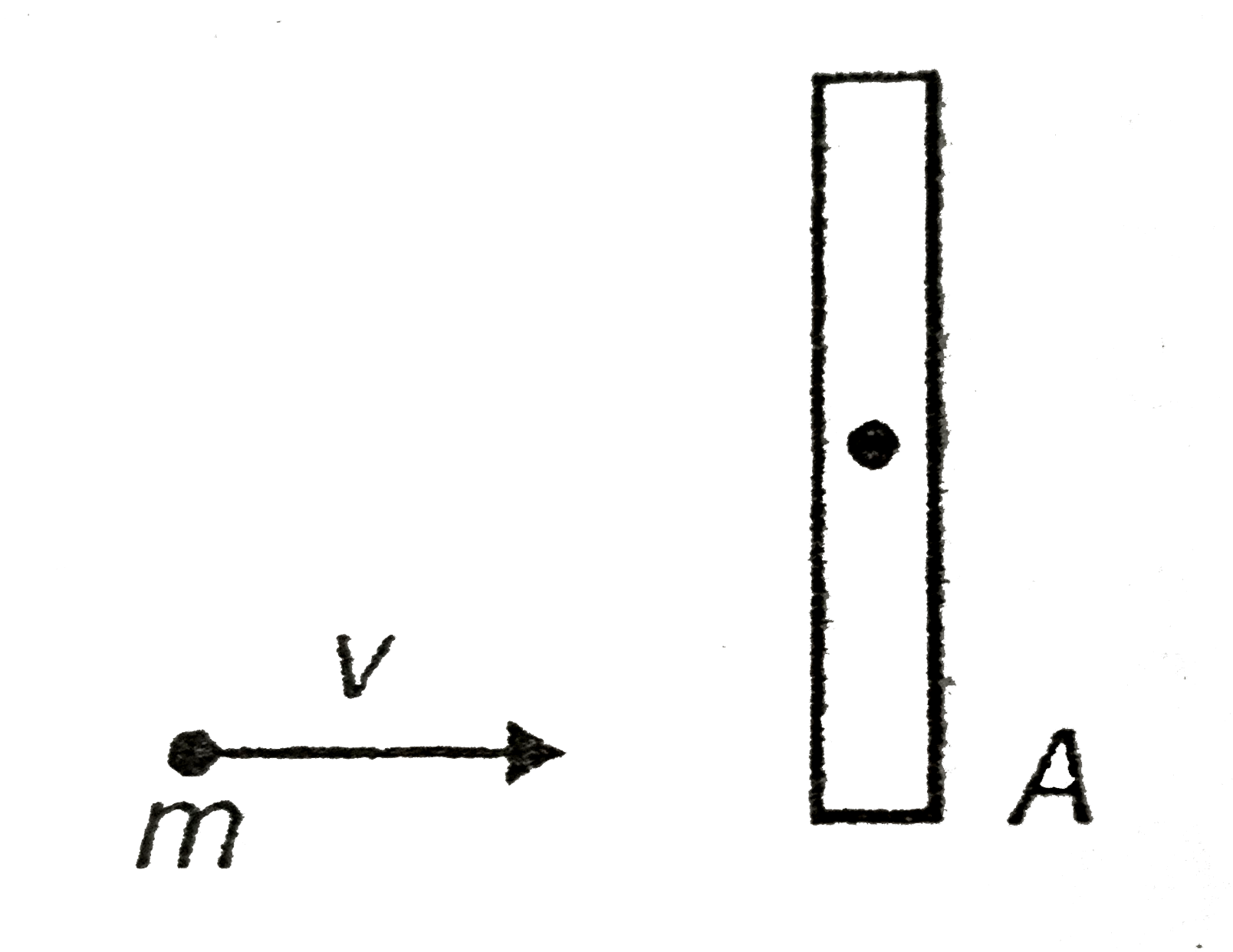
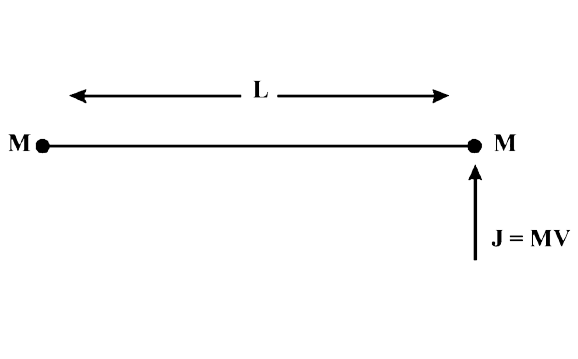
View SolutionConsider a body, shown in figure, consisting of two identical balls, each of mass M connected by a light rigid rod. If an impulse J = MV is imparted to the body at one of its ends what would be it angular velocity?
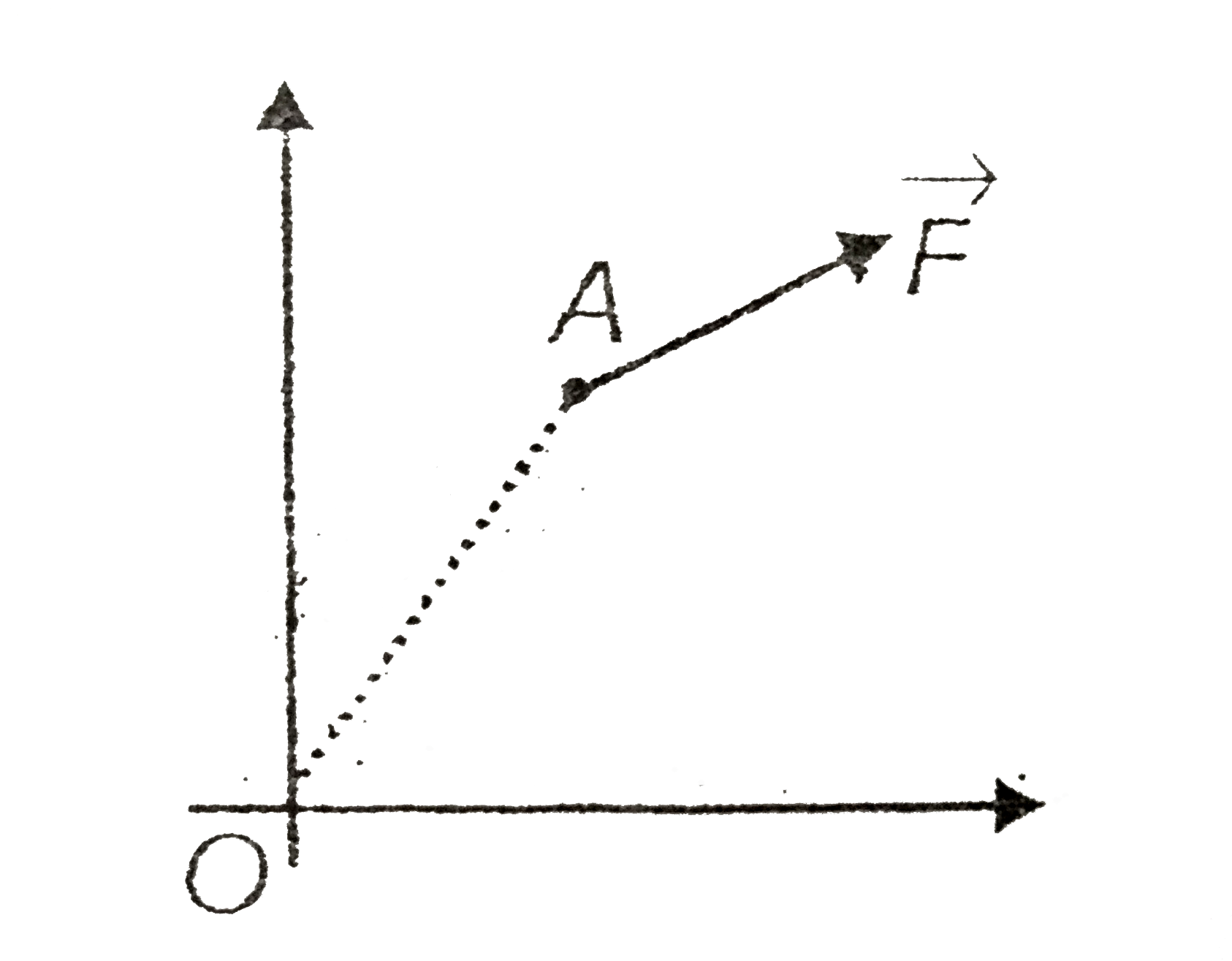
View SolutionA force `vecF=(3hati+4hatj)N` is acting on a point mass `m=((1)/(2))kg` at a point `A(2m,2m)`. Find the angular acceleration of the line `OA` at this instant.
View SolutionIf the earth shrinks to half its present radius, without any change in its mass, then the duration of the day becomes
View Solution
Assignment (Section - B) Objective Type Questions (One option is correct) questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- Assignment (Section - A) Objective Type Questions (One option is correct)
- Assignment (Section - B) Objective Type Questions (One option is correct)
- Assignment (Section - C) Objective Type Questions (More than one option are correct)
- Assignment (Section - D) Linked Comprehension Type Questions
- Assignment (Section - E) Assertion-Reason Type Questions
- Assignment (Section - F) Matrix-Match Type Questions
- Assignment (Section - G) Integar Type Questions
- Assignment (Section - H) Multiple True-False Type Questions
- Assignment (Section - I) Subjective Type Questions
- Assignment (Section - J) Aakash Challengers Questions
- Example
- Illustration
- Try Yourself