Complete Solutions to Example of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH INSTITUTE | Example |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
Two bodies of masses 1kg and 2kg are lying in xy plane at (-1,2) and (2,4) respectively. What are the coordinates of the center of mass?
View SolutionThe coordinates of a triangle `ABC` are `A(1,2)`, `B(4,6)` and `C(-3,-2)`. Three particles of masses `1kg`, `2kg` and `m kg` are placed the vertices of the triangle. If the coordinate of the centre of mass are `((3)/(5),2)`, calculate the mass `m`.
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
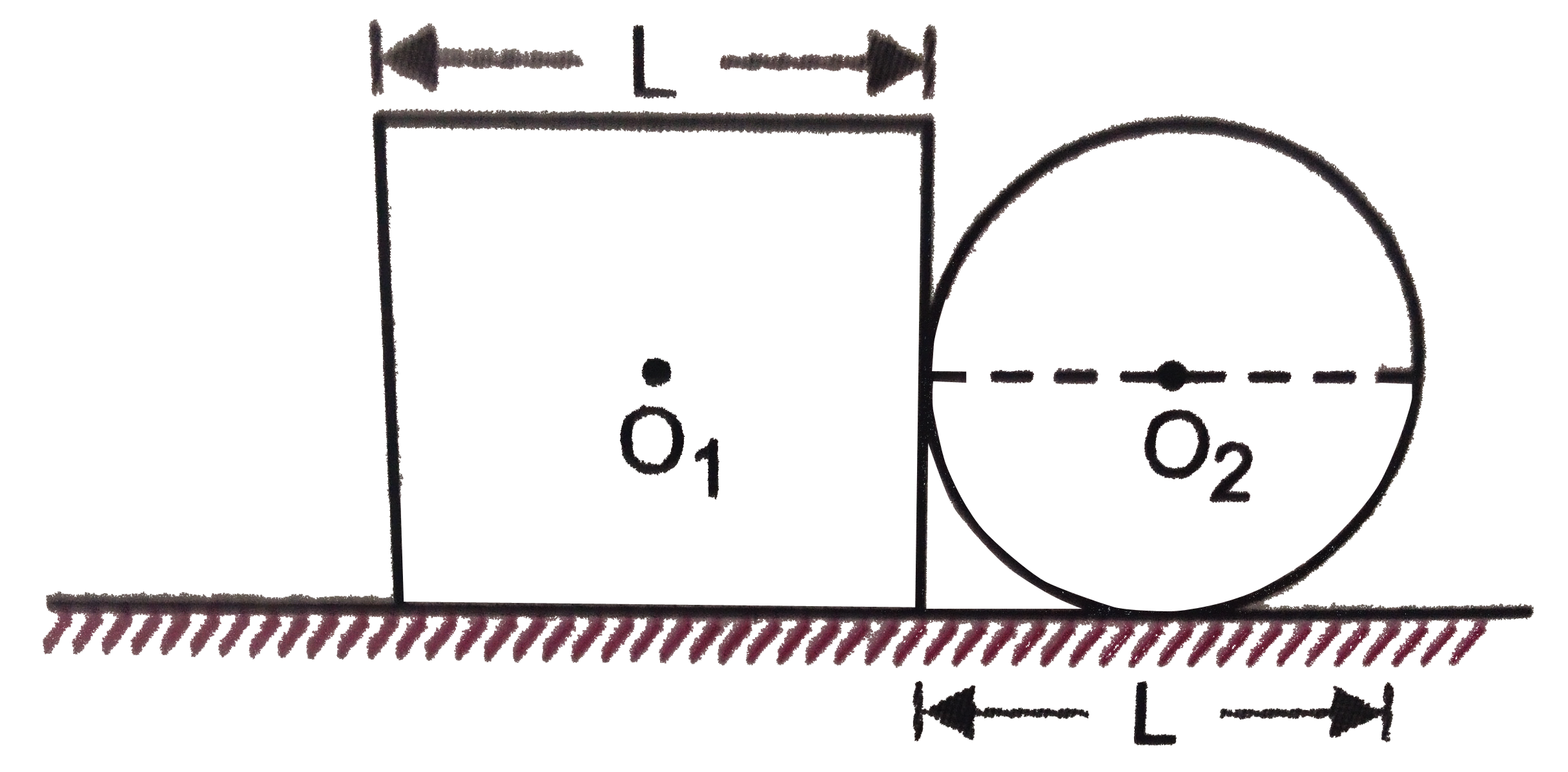
View SolutionA uniform square plate and a disc having same mass per unit area are kept in contact as shown in Fig. The side of square and diameter of circle are both equal to `L`. Locate the position of centre of mass of the system w.r.t. the centre of the square.
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is `R//2`. Find the centre of mass of the remaining part of the disc.

View SolutionTwo particles of mass `1kg` and `2kg` are moving along the same line with speeds `2m//s` and `4m//s` respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View SolutionIf no external force acts on a system
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
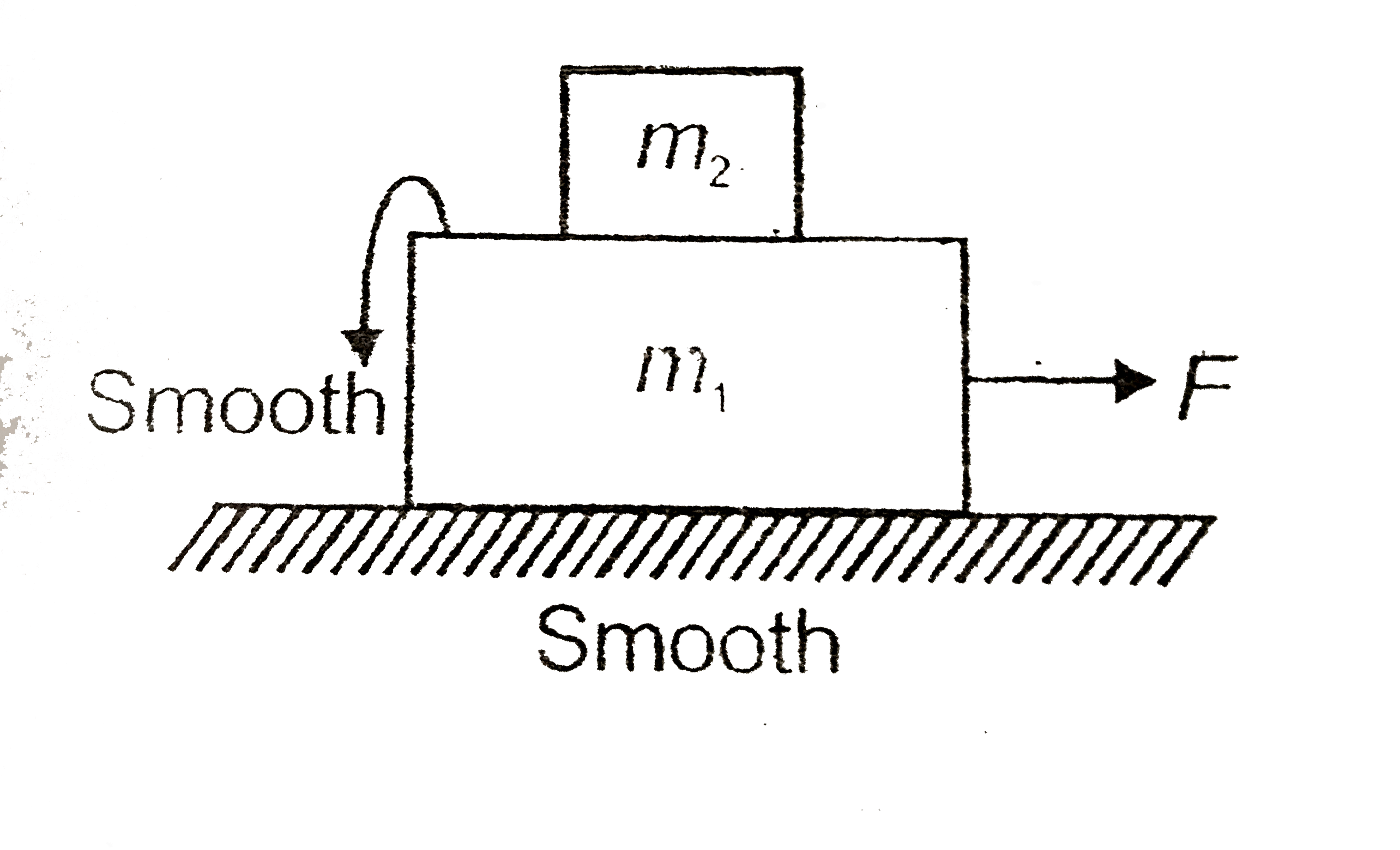
View SolutionAn arrangement of two blocks placed one above the other is shown. There is no fricition any where. A horizontal force `F` acts on one of the blocks as shown. It is required to calculate the acceleration of centre of mass.
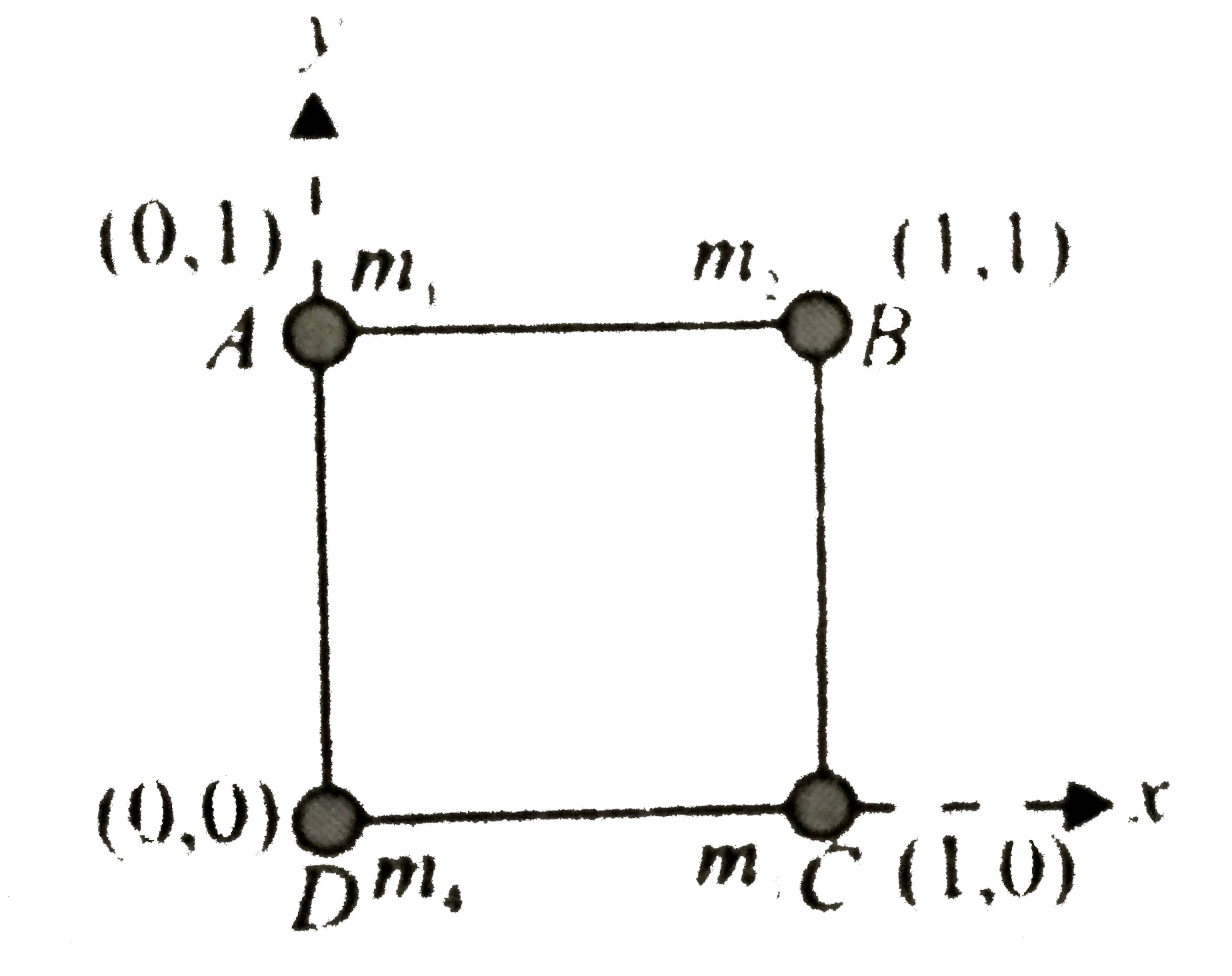
View SolutionFour particles of masses `1 kg, 2kg, 3kg` and `4kg` are placed the four vertices `A,B,C` and `D`, respectively, of a square of side `1m`. Find the position of centre of mass of the particles.
View SolutionThree bodies `A`, `B` and `C` having masses `10kg`, `5kg` and `15kg` respectively are projected from top of a tower with `A` vertically upward with `10m//s`, `B` with `20m//s 53^(@)` above east horizontal and `C` horizontally southward with `15m//s`. Find
`(a)` Velocity of centre of mass of the system.
`(b)`Acceleration of centre of mass of the system.
View Solution`(1)` Find the acceleration of centre of mass of the system shown.
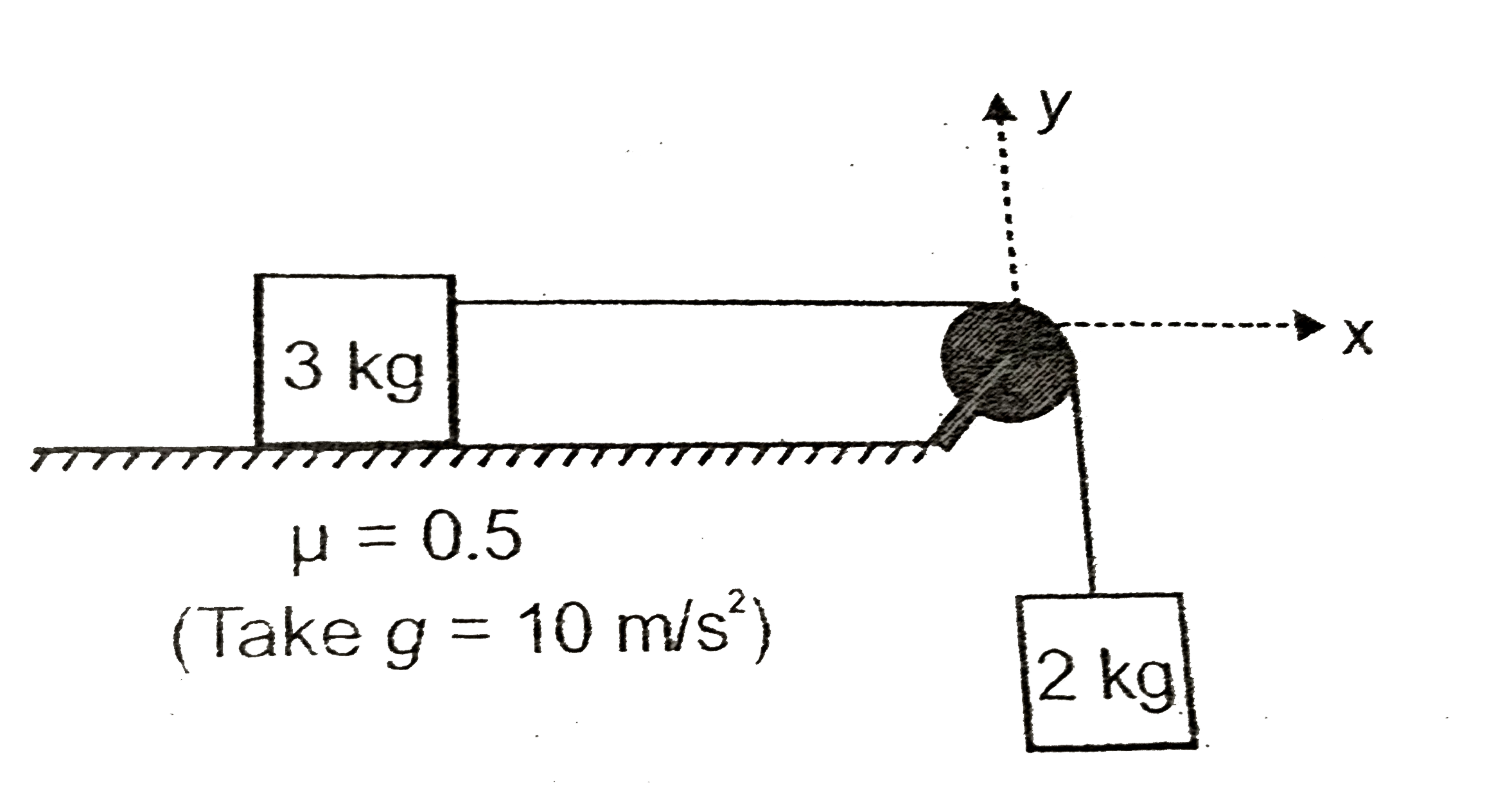
`(ii)` Find the normal reaction applied by the pulley on the thread.
View SolutionFind the scalar and vector products of two vectors `veca=(2hati-3hatj+4hatk)` and `vecb(hati-2hatj+3hatk)`.
View SolutionFind a unit vector perpendicular to each of the vectors `hati+2hatj-3hatk` and `hati-2hatj+hatk`.
View SolutionThe angular position of a particle changes from `3` rad to `7` rad in `2` seconds. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius `20cm`, with a linear velocity of `2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle `theta` with x-axis.
View SolutionThe angular velocity of a flywheel change from `6` rad `s^(-1)` to `18` rad `s^(-1)` in `6` seconds. Calculate its angular acceleration.
View SolutionA force `(hati-2hatj+3hatk)` acts on a particle of position vector `(3hati+2hatj+hatk)`. Calculate the torque acting on the particle.
View SolutionA particle of mass m is projected with speed u at an angle `theta` with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA car of mass 300 kg is travelling on a circular track of radius 100 m with a constant speed of 60 m/s
Calculate the angular momentum ?
View SolutionA torque of 10 Nm is applied on a wheel having angular momentum of `2 kg m^(2)s^(-1)`, calculate the angular momentum of the wheel after 4 seconds.
View SolutionA particle of mass `m` has been thrown with intial speed `u` making angle `theta` with the horizontal ground. Find the angular momentum of the projectile about an axis perpendicular to the plane and passing through the point of projection when the projectile is
`(a)` At the highest point
`(b)` About to hit the ground
View SolutionIn the figure given below, what is the equilibrium of the rod i.e., is it translational or rotational ?

View SolutionIf the Mechanical Advantage of a lever of `100`, when a force of `10N` acts as a distance of `20cm` from the point of fulcrum. Calculate the force acting on the other side of the fulcrum and the distance of that force from the fulcrum.
View SolutionA metal rod of length `50cm` having mass `2kg` is supported on two edges placed `10cm` from each end. A `3kg` load is suspended at `20cm` from one end. Find the reactions at the edges (take `g=10m//s^(2)`)
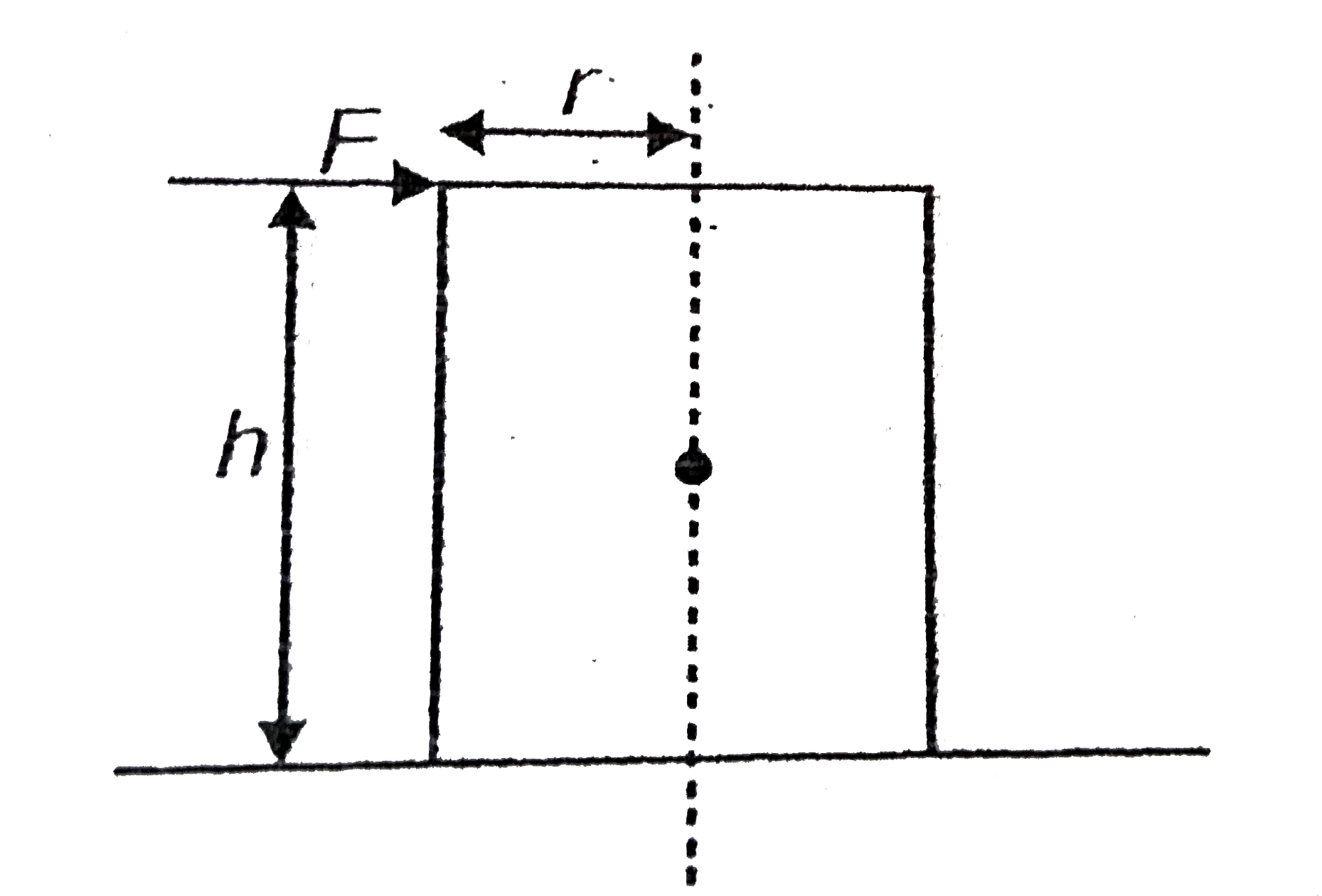
View SolutionA force -`F` is applied at the topmost point of a cylinder of radius `r` and height `h`.
`(a)` If the cylinder remains at rest, then find distance of line of action of normal reaction from center of mass.
`(b)` Find coefficient of friction required so that the cylinder tooples before sliding.
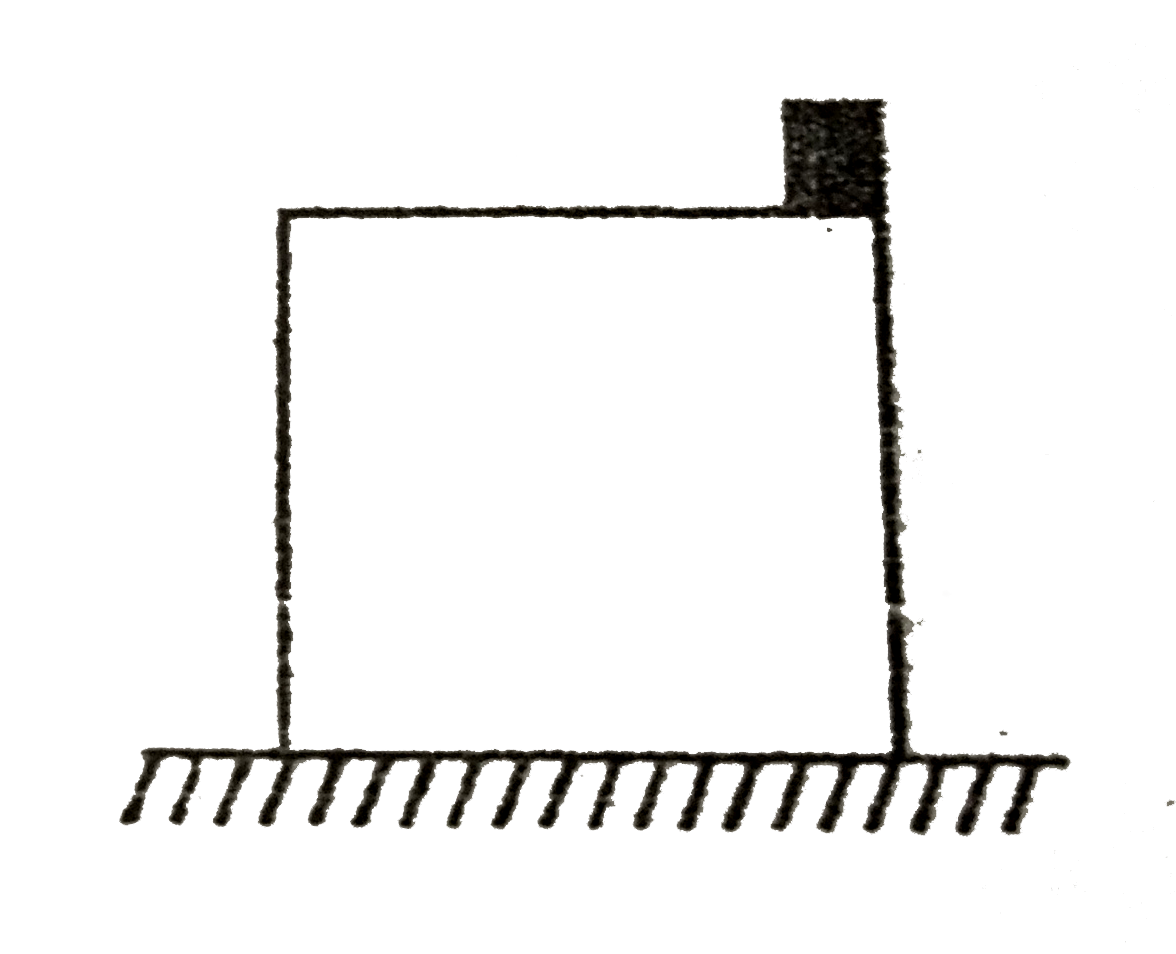
View SolutionA uniform square block of side 'a' and mass 'm' is lying on a horizontal surface. A small block of mass `m` is placed on the top block. Find the distance by which normal reaction is shifted.
View SolutionA cubical block of side 'a' is held at rest, against a rough vertical wall by applying a force `F` acting along the centre. The mass of the block is `m`. Taking acceleration due to gravity as 'g' , determine
`(i)` The minimum coefficient of friction between the block and wall
`(ii)` The torque by normal reaction about the centre of mass
View SolutionThe mass of a uniform circular ring of radius `0.2m` is `0.1kg`. Calculate the moment of inertia of the ring about an axis passing through its center and perpendicular to its surface.
View SolutionThe moment of inertia of a solid cylindrer about its axis of ratation is `(MR^(2))/(2)`. What is the value if the radius of gyration of the cylinder about this axis ?
View SolutionWhat is the moment of inertia of a uniform circular ring about its diameters ?
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe angular velocity of a particle changes from `100` rad `s^(-1)` to `200` rad `s^(-1)` in `4s`. Calculate the angular accelertion of the particle ?
View SolutionThe angular speed of a motor wheel is increased from `600"rpm"` to `1200"rpm"` in `4` seconds. Calculate how many revolutions does the engine make during this time.
View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of `20"rad"//s`, when a torque of `10Nm` is applied to it.
View SolutionA unifrom rod `AB` of length `L` and mass `M` is held horizontally with the help of one light string and a hinge as shown. If string at `B` is burnt suddenly, find out the initial angular acceleration of the rod and the intial reaction force at the hinge.

View SolutionA unifrom rod of mass `m` and length `L` is kept on a horizontal table with `(L)/(4)` length on the table. The end `B` is tied to a string as shown in the figure. The string attached to the end `B` is cut and the rod starts rotating about point `C`. Find the normal reaction from the table on the earth as soon as the string is cut.

View SolutionA thin uniform rod `AB` of mass `m` and length `L` is placed on a smooth horizontal table. A constant horizontal force of magnitude `F` starts acting on the rod at one of the ends `AB`, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as `t=0`, find.
`(a)` Distance moved by centre of mass of the rod in time `t_(0)`.
`(b)` Magnitude of initial acceleration of the end `A` of the rod.
View SolutionA disc shaped pulley of mass `'m'=4 kg` and radius `R=0.5m` can rotate freely about its center. A block of mass `M=2kg` hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
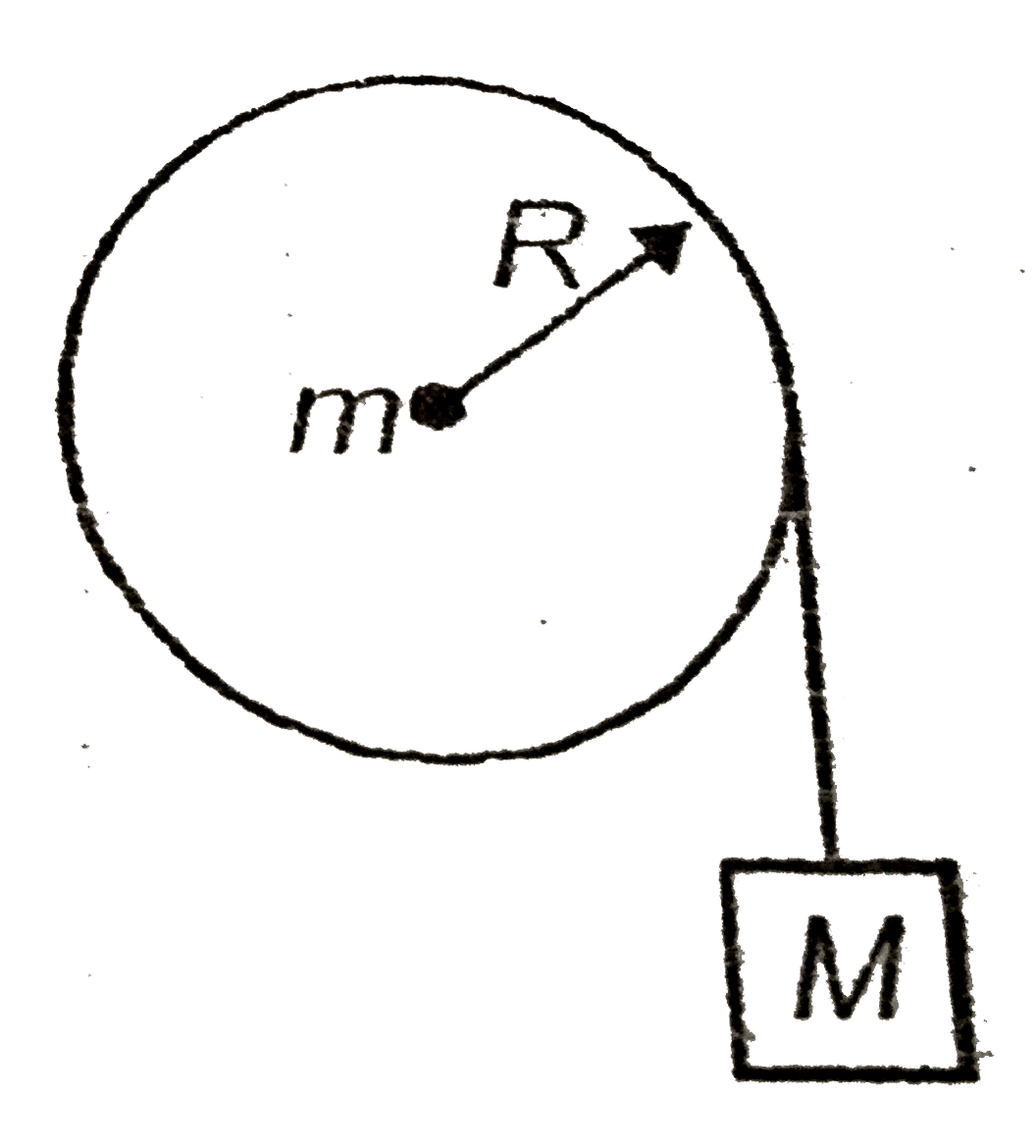
`(a)` Calculate the angular accelerating of the pulley
`(b)` Calculate the tension in the string
View SolutionTwo masses `m_(1)` and `m_(2)` are joined with the help of massless string passing over a pulley of Radius `R` and mass `M`. Assume that string doesn't slip over the pulley. Take `m_(1)=10kg`, `m_(2)=5kg`, `M=10 kg`, `R=1m`.

`(a)` Calculate the acceleration of each book.
`(b)` Calculate the tensions in the thread.
View SolutionCompute the angular acceleration of a wheel having moment of inertia `20kgm^(2)`, when a torque of `10Nm` is applied on the wheel.
View SolutionA flywheel having moment of inertia `20kgm^(2)` rotates about its axis with an angular velocity of `100rads^(-1)`. If the moment of inertia of the flywheel is reduced to `10kgm^(2)` without applying external torque, calculate the new angular velocity of the Flywheel.
View SolutionA particle of mass `m` is projected with a speed `v` at an angle `theta` with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
`(a)` When the particle is at maximum height and
`(b)` When the particle is just about to collide with the horizontal surface
View SolutionThree particles are moving as shown in the figure, Calculate the angular momentum of the third particle `C`, so that the angular momentum of system about point `O` becomes zero.

View SolutionA cylinder of mass `5kg` and radius `10cm` is moving on a horizontal surface with speed. `5m//s` and angular speed about axis through `C.M. 10rad//s`. Find the angular momentum of the cylinder about point of contact.
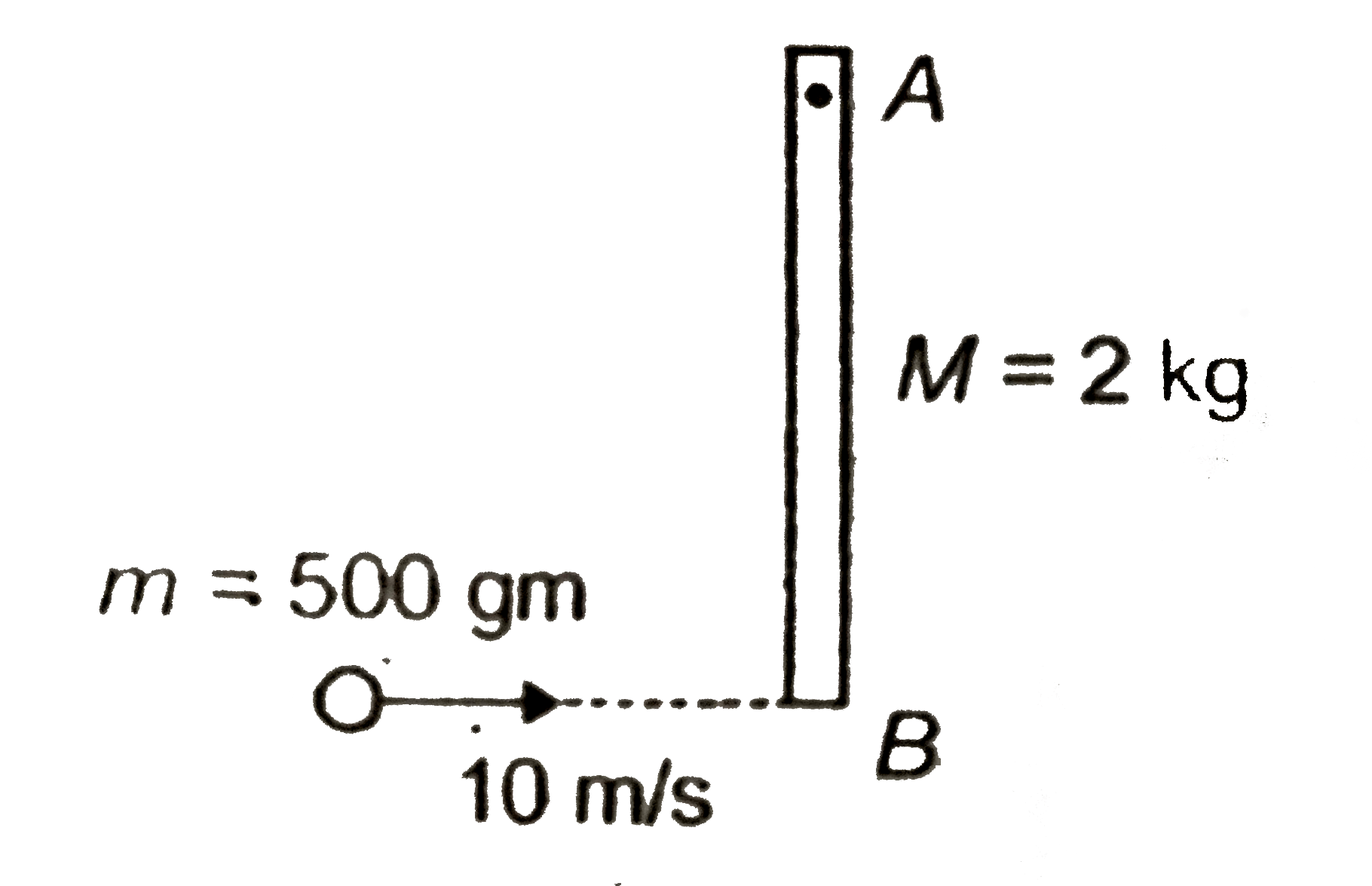
View SolutionA rod of mass `2kg` and length `1m` is pivoted at one end `A` and kept on a smooth surface. A particle of mass `500gm strikes the other end B` of the rod and sticks to the rod. If particle was moving with the speed of `10m//s`, what is the angular speed of the rod after collision ?
View SolutionA rod AB of mass `M` and length L is lying on a horizontal frictionless surface. A particle of mass `m` travelling along the surface hits the end A of the rod with a velocity `v_(0)` in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio `m//M`
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Find the linear speed of the point P a time `piL//3v_(0)` after the collision.
View SolutionA rod of mass `M` and length `L` is falling vertically with speed `v`. Suddenly its one end gets stuck in a friciitonless hook. Find the angular velocity of the rod just after its end gets struck.

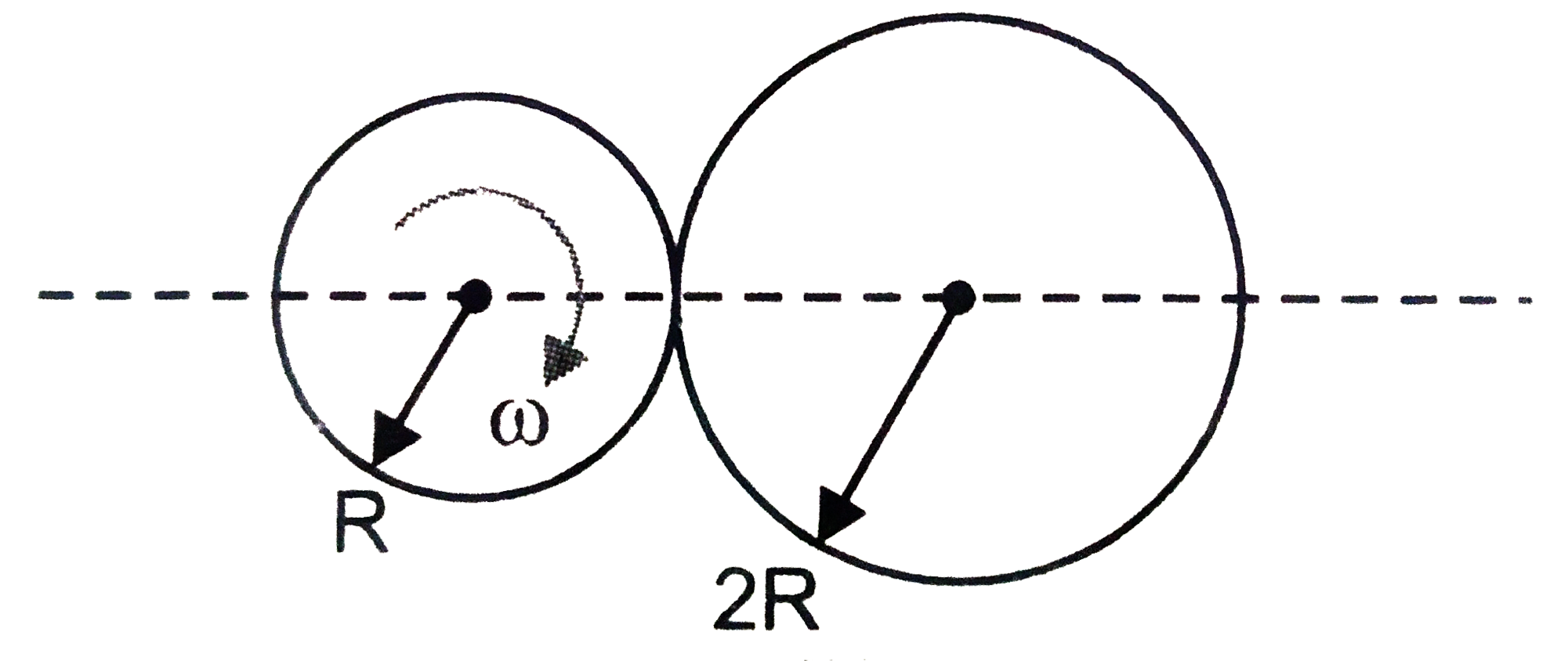
View SolutionTwo discs of radii `R and 2R` are pressed against each other. Initially, disc with radius `R` is rotating with angular velocity `omega` and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is `I` and of bigger disc is `2I` about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
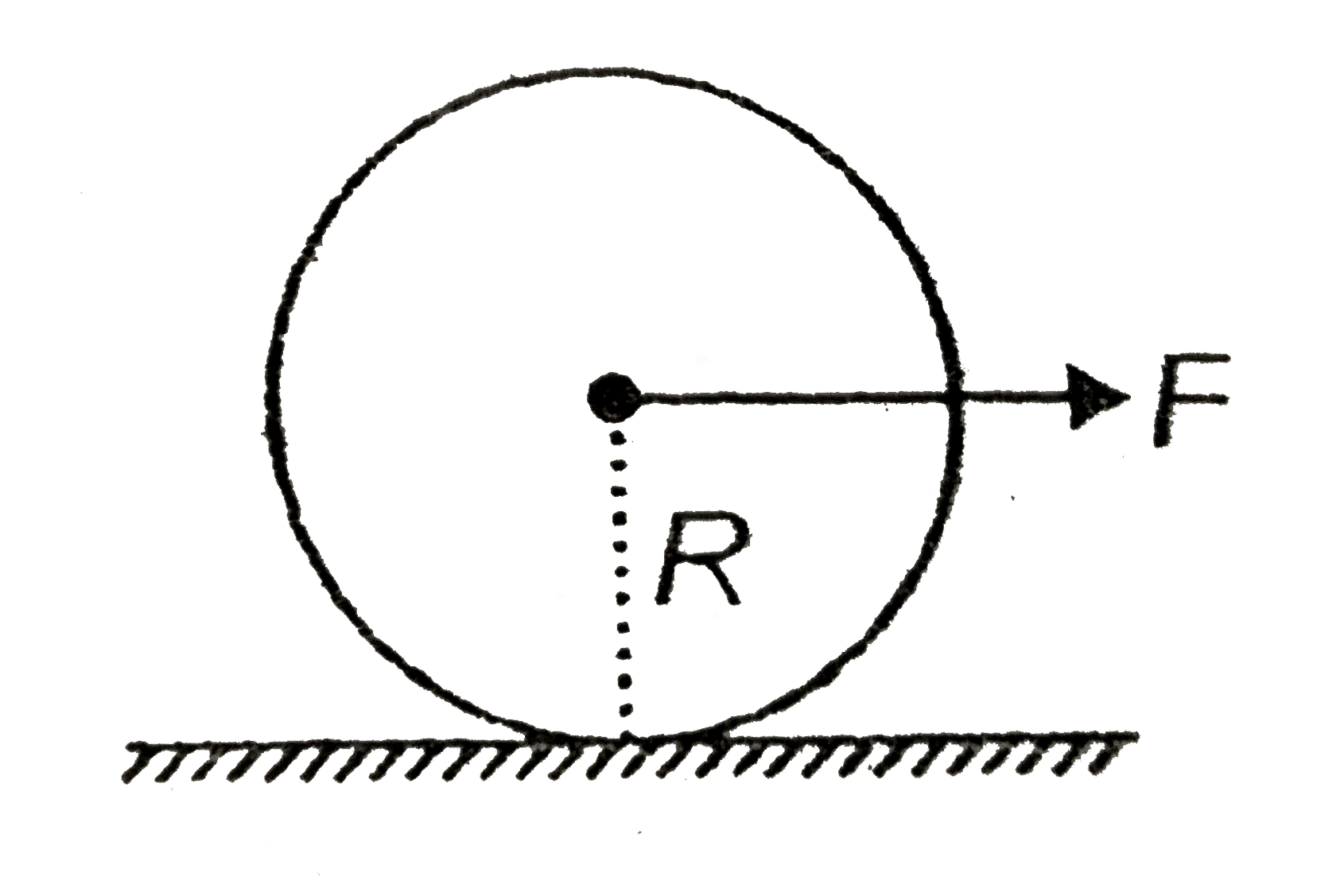
View SolutionA force `F` is applied at center of a uniform round object of mass `m` radius `R` and moment of inertia about its centre of mass `I_(cm)`. Find (if `(I_(cm))/(mR^(2))=k`).
`(a)` Acceleration of center of the round object if it rolls without slipping.
`(b)` Minimum coefficient of fricition required so that the round object rolls without slipping.
View SolutionA force `F` is applied on a disc at it's centre. Find acceleration of center of mass in the case of pure rolling and also find minimum coefficient of fricition required for pure rolling.
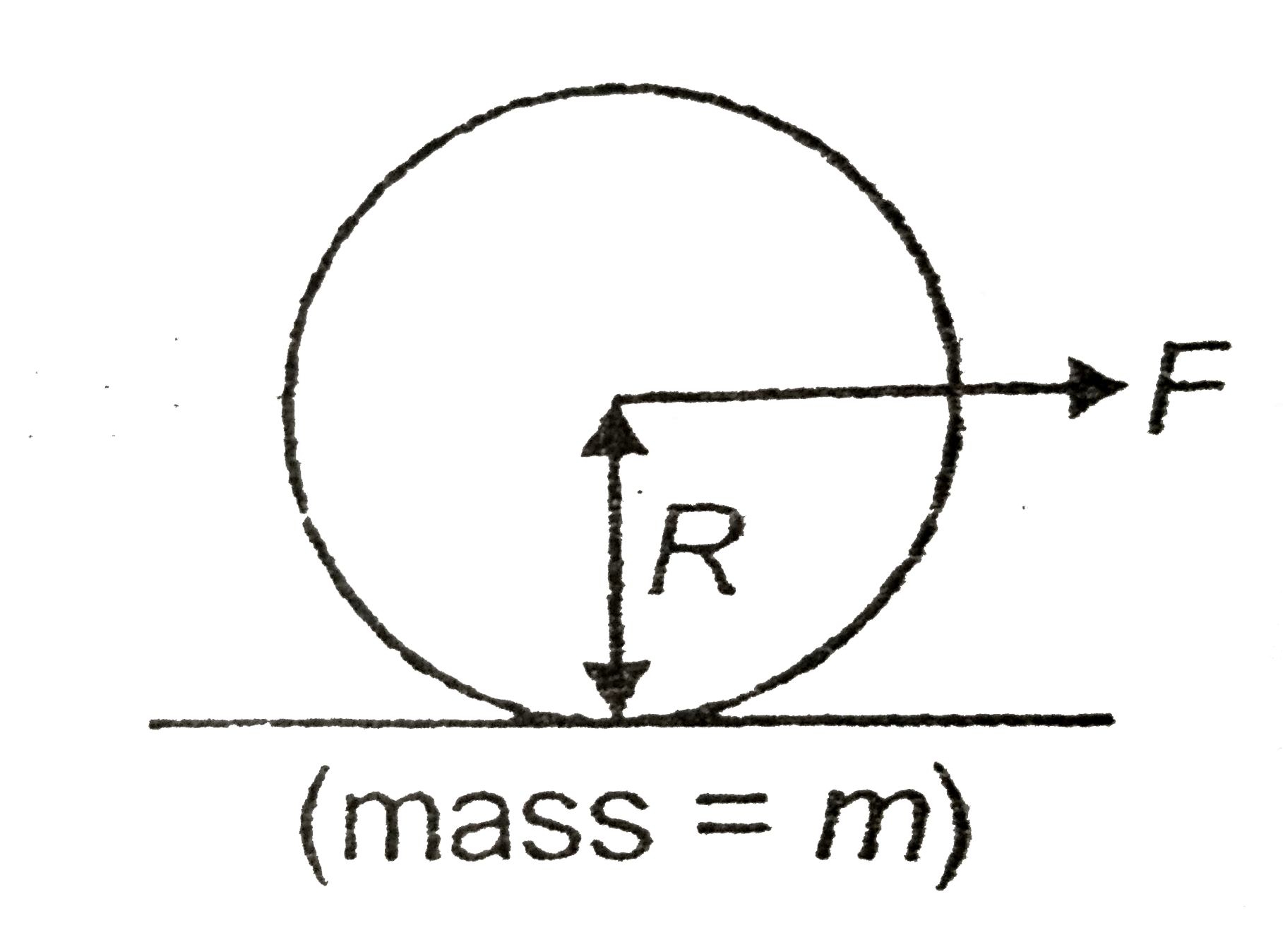
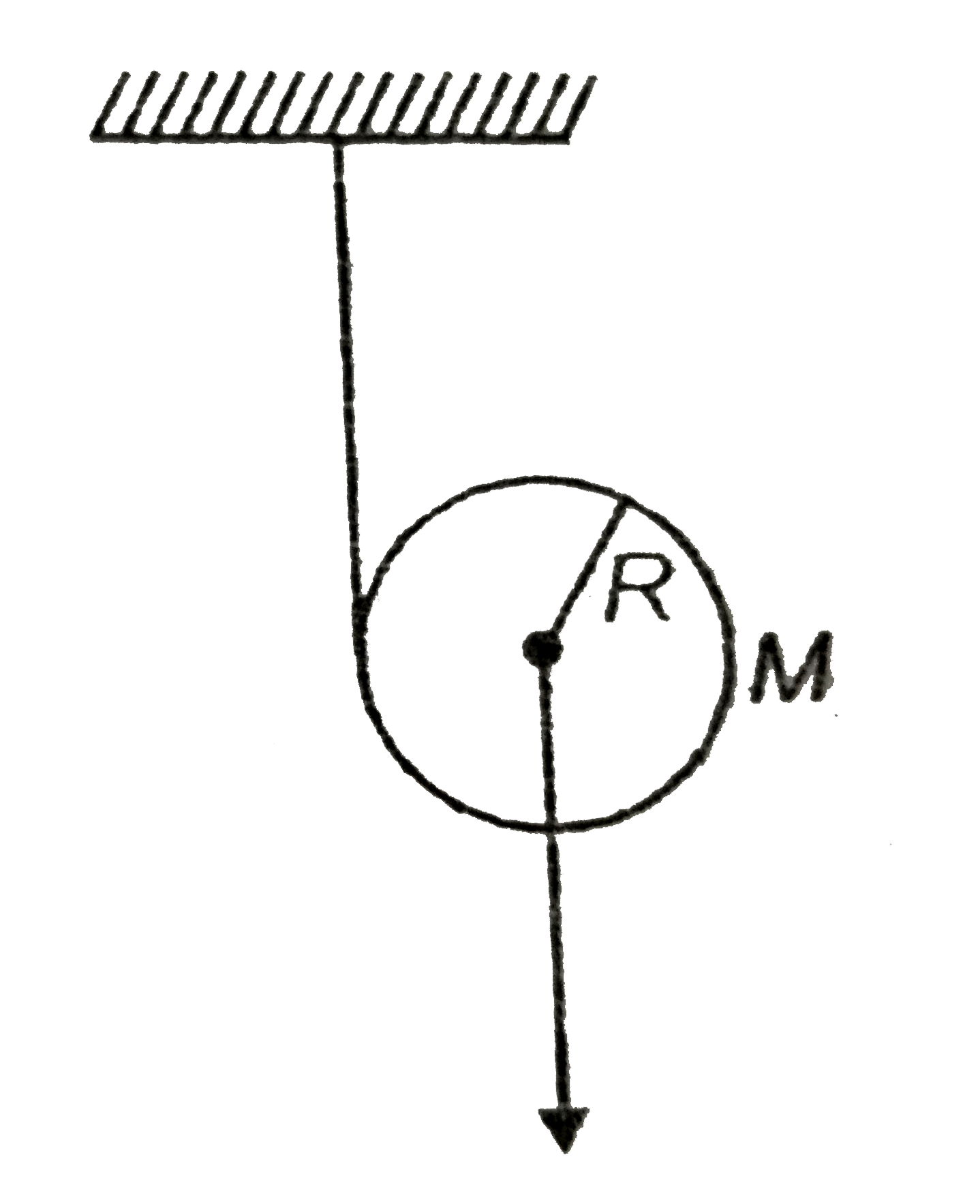
View SolutionA uniform round object of mass `M`, radius `R` and moment of inertia about its centre of mass `I_(cm)` has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take `(I_(cm))/(MR^(2))=k`]
View SolutionA disc of mass `M` has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
View SolutionA solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is `mu=0.5` and radius `R`, then find
`(a)` Time when linear velocity becomes zero
`(b)` Angular velocity at that instant

View SolutionA uniform round object of mass `m`, radius `R` and moment of inertia about its centre of mas `I_(cm)` is thrown with speed `v`. (Without any rotation) on a rough horizontal surface of coefficient of fricition `mu`. Find (take `(I_(cm))/(mR^(2))=k`)
`(a)` Time after which slipping stops
`(b)` Speed of the round object after slipping stops
`(c )` Angular speed of the round object after slipping stops
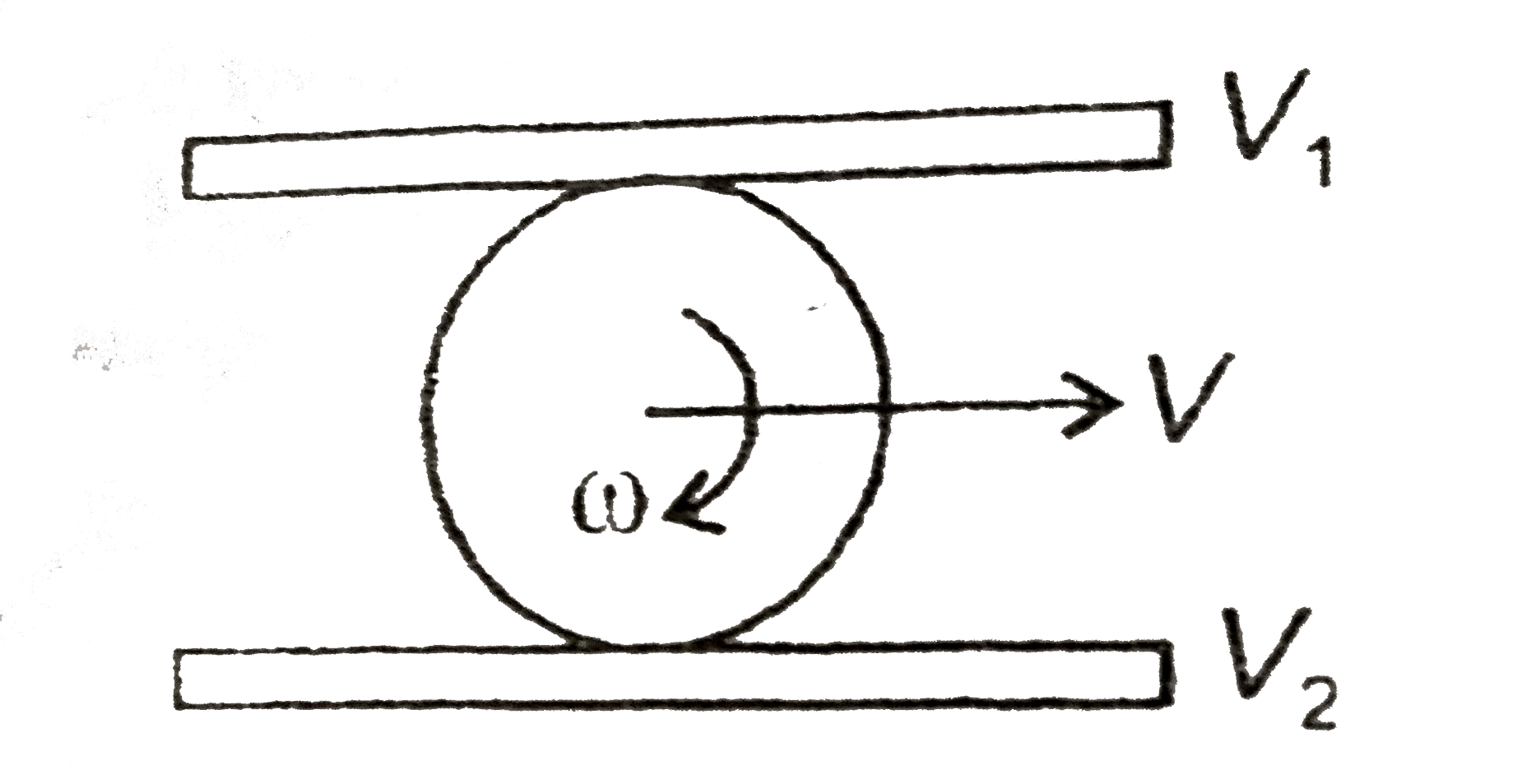
View SolutionA sphere of radius `R` rolls without slipping between two planks as shown in figure. Find
`(a)` Speed of centre of sphere
`(b)` Angular velocity of the sphere
View SolutionConsider a cylinder of mass `M` and radius `R` lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force `F` is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

`(a)` what are the directions of the fricition forces acting at `A` and `B` on the plank and the cylinder ?
`(b)` Calculate the acceleration of the cylinder.
`(c )` Find the value of frictional force at `A` & `B`.
View SolutionCalculate the kinetic energy of rolling ring of mass 0.2 kg about an axis passing through its centre of mass and perpendicular to it, if centre of mass is moving with a velocity of 3 m/s.
View SolutionA solid sphere is rolling down an inclined plane without slipping of height 20 m. Calculate the maximum velocity with which it will reach the bottom of the plane `(g = 10 m//s^(2))`
View SolutionA cylinder of mass `m` and radius `R` is kept on a rough surface after giving its centre a horizontal speed `v_(0)`. Find the speed of the centre of the cylinder when it stops slipping.
View Solution
Example questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- Assignment (Section - A) Objective Type Questions (One option is correct)
- Assignment (Section - B) Objective Type Questions (One option is correct)
- Assignment (Section - C) Objective Type Questions (More than one option are correct)
- Assignment (Section - D) Linked Comprehension Type Questions
- Assignment (Section - E) Assertion-Reason Type Questions
- Assignment (Section - F) Matrix-Match Type Questions
- Assignment (Section - G) Integar Type Questions
- Assignment (Section - H) Multiple True-False Type Questions
- Assignment (Section - I) Subjective Type Questions
- Assignment (Section - J) Aakash Challengers Questions
- Example
- Illustration
- Try Yourself