Complete Solutions to Assignment (Section - I) Subjective Type Questions of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH INSTITUTE | Assignment (Section - I) Subjective Type Questions |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
Figure shows a right angled triangle of uniform mass per unit area, attached with rectangular lamina of sides `3m` and `5m` made of same material. Find the centre of mass of the system.

View SolutionA particle of mass `m` is moving anticlockwise, in a circle of radius `R` in `x-y` plane with centre at `(R,0)` with a constant speed `v_(2)`. If is located at point `(2R,0)` at time `t=0`. A man starts moving with a velocity `v_(1)` along the positive `y`-axis from origin at `t=0`. Calculate the linear momentum of the particle w.r.t. man as a function of time.
View SolutionTwo blocks `A` and `B` of masses `m` and `2m` are placed on a smooth horizontal surface. Block `B` is given a speed of `3m//s`. Find
`(i)` The maximum speed of `A`
`(ii)` The minimum speed of `B`.
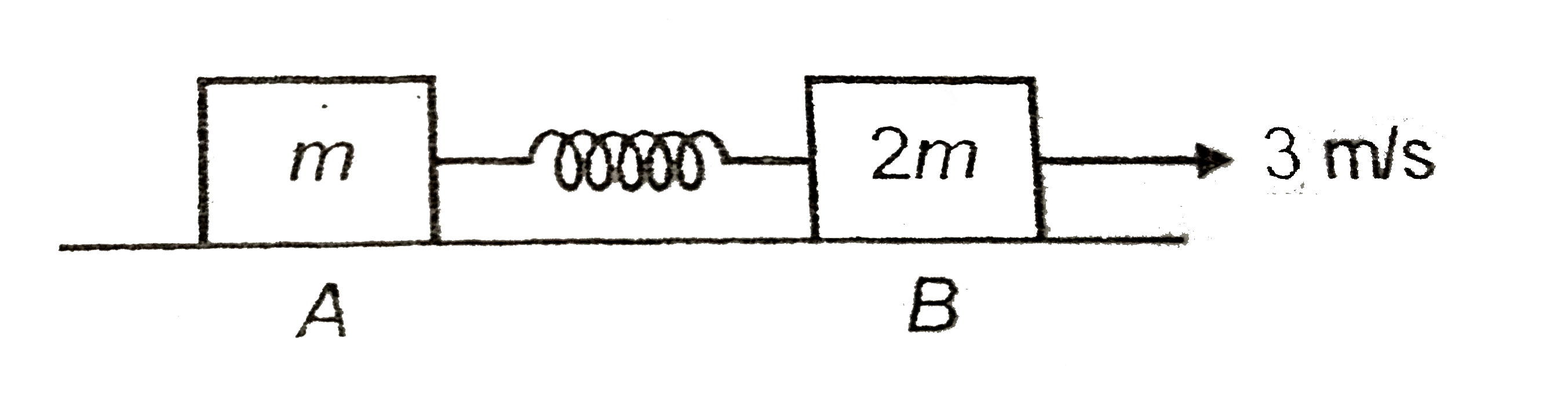
View SolutionA ball is projected from ground with a speed `70m//s` at an angle `45^(@)` with the vertical so that it strikes a vertical wall at horizontal distance `(490)/(3)m` from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionA collar `B` of mass `m` is at rest and when it is in the position shown, the spring is unstretched. If another collar `A` of mass `(m)/(n)` strikes it so that `B` slides a distance `4m` on the smooth rod before momentarily stopping, determine the velocity of `A` just after the impact. The coefficient of restitution is `e`. The spring constant is `k`.
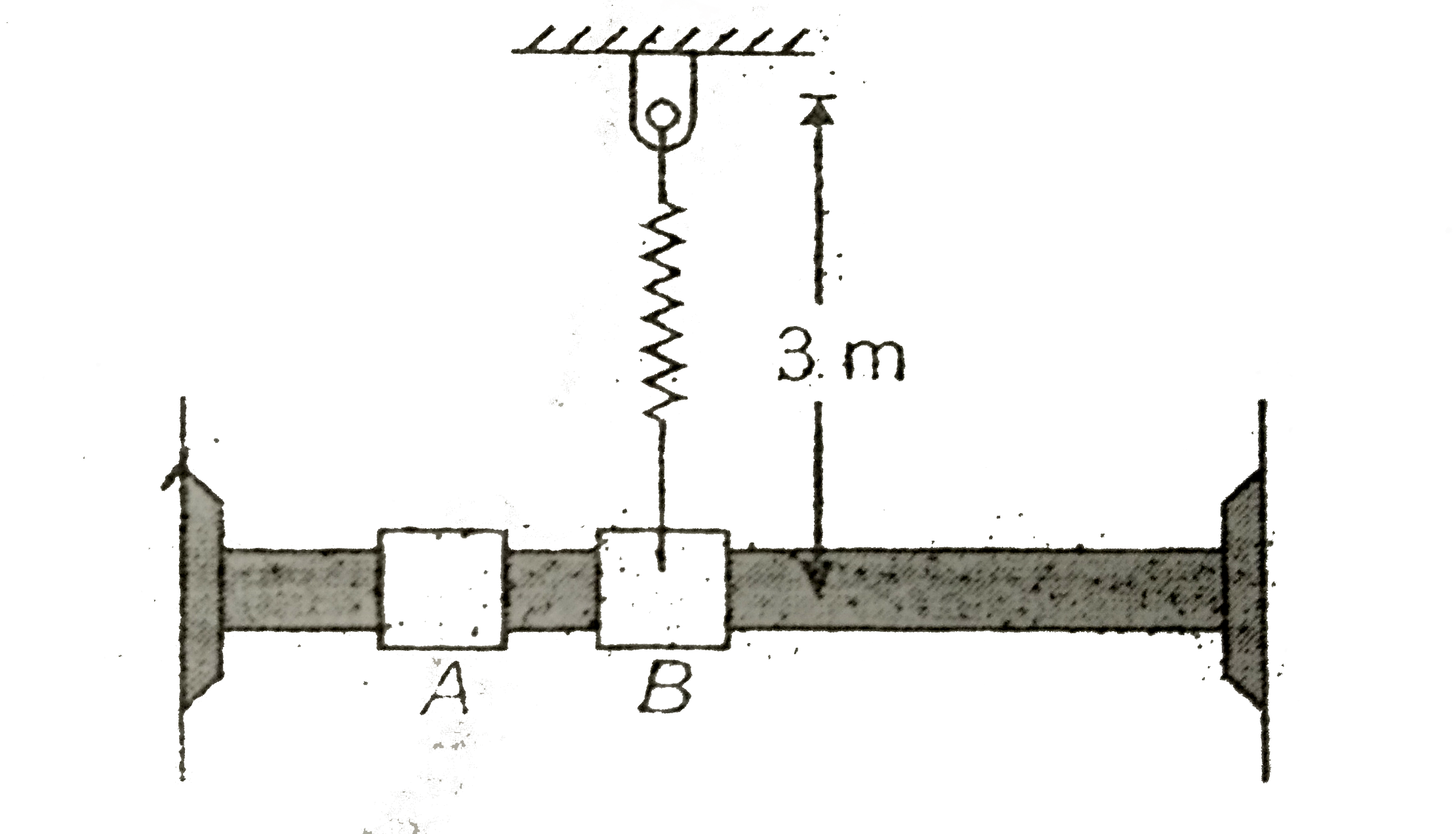
View SolutionA uniform disc (of mass `M` and radius `a`) has a hole (of radius `b`) drilled through it. The centre of the hole is at a distance `c` from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View Solution
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance `h` above the centre line as shown in figure. The ball leaves the cue with a speed `v_(0)` and because of its backward slipping eventually acquires a final
speed `(9)/(7)v_(0)` show that `h=(4)/(5)R`
Where `R` is the radius of the ball.
View SolutionA semicircle disc of mass `M` and radius `R` is held on a rough horizontal surface as shown in figure. The centre of mass `C` of the disc is at a distance of `(4R)/(3pi)` from the point `O`. Now the disc is released from this position so that it starts rolling without slipping. Find
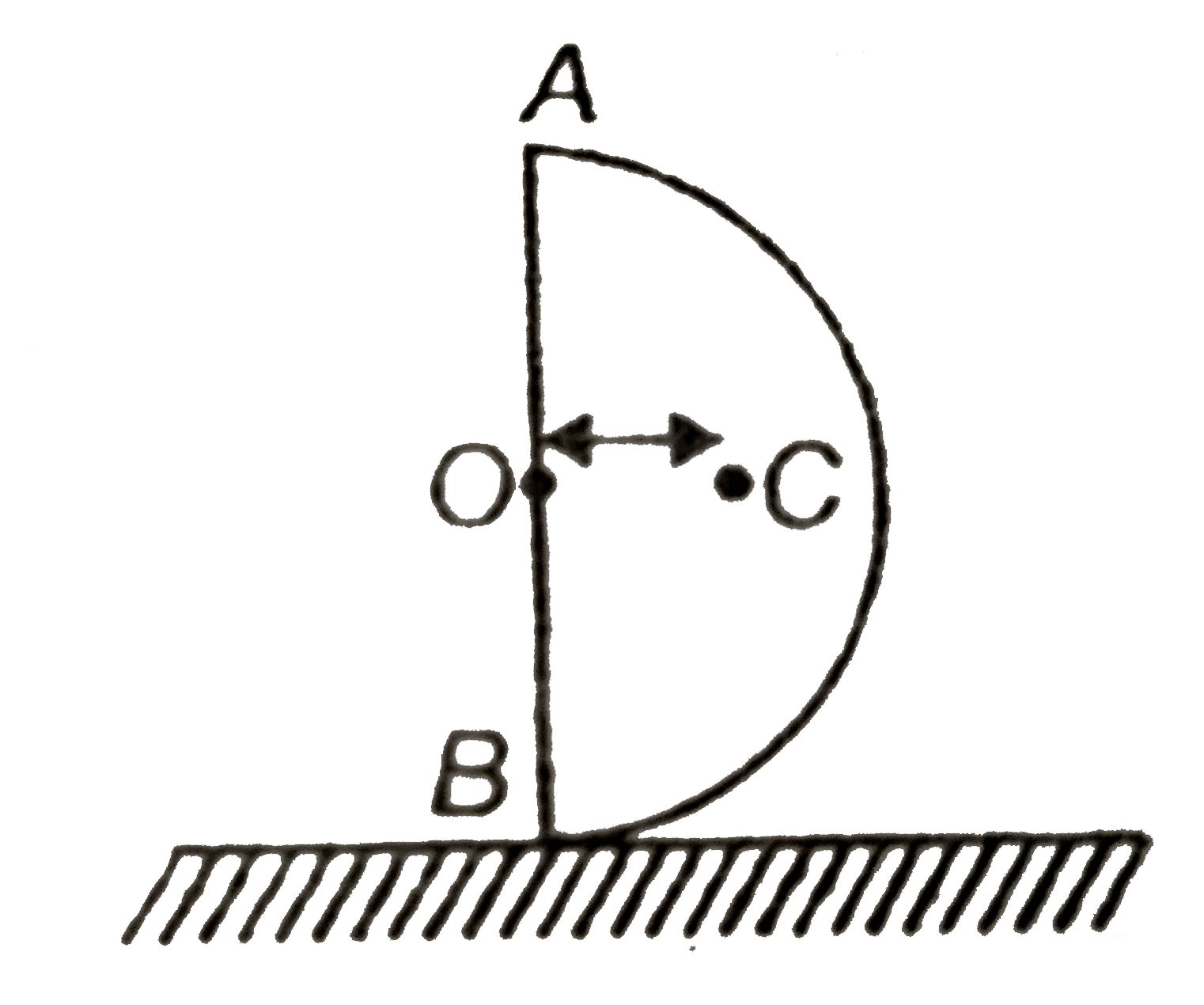
`(a)` The angular acceleration of the disc at the moment it is relased from the given position.
`(b)` The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View Solution
Assignment (Section - I) Subjective Type Questions questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- Assignment (Section - A) Objective Type Questions (One option is correct)
- Assignment (Section - B) Objective Type Questions (One option is correct)
- Assignment (Section - C) Objective Type Questions (More than one option are correct)
- Assignment (Section - D) Linked Comprehension Type Questions
- Assignment (Section - E) Assertion-Reason Type Questions
- Assignment (Section - F) Matrix-Match Type Questions
- Assignment (Section - G) Integar Type Questions
- Assignment (Section - H) Multiple True-False Type Questions
- Assignment (Section - I) Subjective Type Questions
- Assignment (Section - J) Aakash Challengers Questions
- Example
- Illustration
- Try Yourself