Complete Solutions to EXAMPLE of chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC POTENTIAL AND CAPACITANCE |
| AAKASH INSTITUTE | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J . What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View SolutionFind the change in electric potential energy , `Delta U` as a charge of (a) `2.20 xx 10^(-6) C.` (b) `- 1.10 xx 10^(-6) C ` moves from a point A to a point given that the change in electric potential between these points is `DeltaV= V_(B) -V_(A) = 24.0 V`
View SolutionA particle of mass m and positive charge q is released from point A. Its speed is found to be v when it passes through a point B. which of the two points is at higher potential ? What is the potential difference between the points?
View SolutionAn electron , with charge of `-1.60 xx 10^(19) C`, accelerates from rest through a potential difference V. A proton , with a charge of `+ 1.60 xx 10^(-19) C `, accelerates from rest through a potential difference `-V` . Is the final speed of the electron (a) more than , (b) less than , or (c ) same as the final speed of the proton ?
View SolutionA charge of 10C is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J. What is the potential difference `V_(A)-V_(B)`?
View SolutionSuppose the an electron in the picture tube of a televisoin set is accelerated from rest through a potential differnece `V_(b)-V_(a)= V_(ba) = +5000V`.
(a) What is the change in electric potential energy of the electron?
(b) What is the speed of the electron `( m = 9.1 xx 10^(-31) kg)` as a result of this acceleration ?
View SolutionDetermine the potential at a point 0.50 m (i) from a`+20 muC` potential charge (ii) from a`-20 muC` point charge.
View SolutionFigures (a) and (b) show the field lines of a positive and negative point charge respectively.

(a) Give the signs of the potential difference `V_(P)-V_(Q), V_(B)-V_(A)`.
(b) Give the sign of the potential energy difference of a small negative charge between the points Q and P, A and B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
(d) Give the sign of the work done by the external agency in moving a small negative charge from B to A.
(e) Does the kinetic energy of a small negative charge increase or decrease in going from B to A?
View SolutionThe classical model of a hydrogen atom in its normal unexcited configuration has an electron that revolves around a proton at a distance of `5.3xx10^(-11)` m.
(a) What is the electric potential due to the proton at the position of electron ?
(b) Determine the electrostatic potential energy between the two particles.
View SolutionWhat minimum work must be done by an external force to bring a charge `q=3.00 muC` from a great distance away (take `t = infty`) to a point `0.500 m` from a charge ` = 20.0 muC` ?
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin
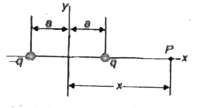
(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .
View SolutionA charge `q_(1) = 2.00 mu C` is located at the origin , and a charge `q_(2) = - 6.00 mu C ` is located at `( 0,3.00 ) m`.
(a) Find the total electric potential due to these charges at the point `P` hose coordinates are ( 4.00,0) m .
( b) Find the change in potential energy of the system of two charges plus a charge `q_(3)= 3.00 muC` as the latter charge moves from infinity to point P .
View SolutionSuppose that three point charges, `q_(a),q_(b) and q_(c)` are arranged at the vertices of a right-angled triangle, as shown. What is the absolute potential at the position of the third charge, if `q_(a)= -6.0 muC,q_(b) = +4.0 muC,q_(c) = +2.0 muC,a=4.0 m and b=3.0 m` ?

View SolutionTwo charges `3 xx 10^(-8) C` and `-2 xx 10^(-8)C` are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
View SolutionIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
View SolutionA spherical oil drop, radius `10^(-4)` cm has on it at a certain a total charge of 40 electrons. Calculate the energy that would be required to place an additional electron on the drop.
View SolutionA spherical drop of water carrying a charge of `3 xx 10^(-19)C` has a potential of 500 V at its surface. What is the radius of the drop ? If two drops of the same charge and the same radius combine to form a single spherical drop, what is the potential at the surface of the new drop ?
View SolutionA charge Q is distributed over two concentric conducting thin spherical shells radii r and R `(R gt 1)` . If the surface charge densities on the two shells are equal, the electric potential at the common centre is:
View SolutionTwo charges `+q and -q`, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
View SolutionA proton is fixed at origin. Another proton is released from rest, from a point at a distance `r` from origin. Taking charge of portion as e and mass as `m`, find the speed of the proton (i) at a distance `2r` from origin (ii) at large distance from origin.
View SolutionThree charges are placed along x- axis at `x = -a , x=0` and `x=a` as shown . Calculate the potential energy of the system.

View SolutionCalculate the work required to be done to make an arrangement of three particles each having a charge `+q` such that the particles lie at the vertices of an equilateral triagnle of side a. What work will be doen by electric field when the particles are shifted away so that the side of triangle becomes 2a ?
View SolutionDetermine the interaction energy of the point charge located at the corners of a square with the side a in the circuits shown in figure.

View SolutionWhen an electric dipole is placed in a uniform electric field making angle `theta` with electric field, it experiences a torque `tau`. Calculate the minimum work donein changing the orientation to `2 theta`.
View SolutionA molecule of a substance has a permanent electric dipole moment of magnitude `10^(-30)` cm. A mole of this substance is polarised by applying a strong electrostatic field of magnitude `10^(7) V m^(-1).` The direction of field is charged by an angle `60^(@).` The heat released by the substance in aligning its dipole along the new direction of the field is
View SolutionA charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.
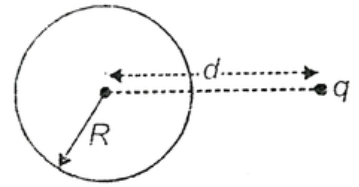
Strategy `:` The net electric field inside the conductor is zero. This is produced by induced charges and the external charge.
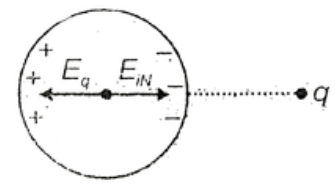
View SolutionA point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad `R(lt r)`. The potential at any point on the sphere is
View SolutionA thin metallic spherical shell carries a charge Q on it. A point charge `Q_(1)` is placed at the centre of the shell and another charge q is placed outside as shown in figure ahead. All the charges are positive . Discuss the various forces acting on `Q_(1)`.

View SolutionTwo metallic spheres of radii a and b are placed far away from each other and re connected by a thin conducting wire. A charge Q is given to one of the sphere. Calculate the charge on each sphere at electrostatic equilibrium
View SolutionA capacitor of `0.75 muF` is charged to a voltage of 16 V. What is the magnitude of the charge on each plate of the capacitor ?
View SolutionA parallel plate capacitor is constructed with plates of area `0.0280 m^(2)` and separation `0.550 mm`. Find the magnitude of the charge on each plate of this capacitor when the potential between the plates is `20.1 V`

View SolutionA parallel -plate capacitor is connected to a battery that maintains a constant potential difference V between the plates. If the plates are pulled away from each other, increasing their separation does the magnitude of the charge on the plates (a) increase (b) decrease or (c ) remain the same ?
View SolutionIn the arrangement shown find the equivalent capacitance between A and B.
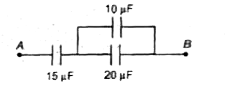
Strategy : First mark different junctions (nodes ) in the circuit. A node is a point where more than two wires are connected.
View SolutionThe arrangement shows a part of complete circuit . The potentials at points A and B are `V_(1)` and `V_(2)` respectively . Find the potential at point P .

Strategy `:` The two capacitors `C_(1)` and `C_(2)` are connected in series . Therefore the charge on both of the capacitors is same. Let the potential at P is V.
View SolutionFor the following arrangement, find the equivalent capacitance between A and B
 .
.
View SolutionFind the charge on each plate given area of each plate is A and separation between two consecutive plates is d.

View SolutionAn air-cored capacitor of plate area A and separation d has a capacity C. Two dielectric slabs are inserted between its plates in two different manners as shown. Calculate the capacitance in each case.

View SolutionCalculate the capacitance of the parallel plate capacitor shown in the following figure between point X and Y.

View SolutionTwo capacitors of capacitance `C_(1)=2muF and C_(2) = 8 muF` are connected in series and the resulting combination is connected acorss 300 V. Calculate the charge, potential difference and energy stored in the capacity separately.
View SolutionAn air-cored parallel plate capacitor having a capacitance C is charged by connecting it to a battery. Now, it is disconnected from the battery and a dielectric slab of dielectric constant K is inserted between its plates so as to completely fill the space between the plates. Compare `:`
(I) Initial and final capacitance
(ii) Initial and final charge.
(iii) Initial and final potential difference.
(iv) Initial an final electric field between the plates.
(v) Initial and final energy stored in the capacitor.
View SolutionA parallel plate capacitor of capacitance C has been charged so that the potential difference between its plates is V. Now the plates of this capacitor are connected to another uncharged capacitor of capacitance 2 C . Find the common potential acquired by the system and loss of energy .
View SolutionA point charge `q_(0)` is moved slowly from the centre of a ring R, ( that is carrying a charge q) to a distance x from its centre along its axis. What is the work done by the external agent in this process ?
Strategy `:` According to work energy theorem, if there is no change in kinetic energy, we have
`W_(ext)+ W_(E ) = 0`
`implies W _(ext) = - W_(E )`
`= - q_(0)(V_(A)-V_(B))`
View SolutionA point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
View SolutionCalculate the self potential energy of charge q distributed over the surface of a hollow sphere of radius R. What happens to this self energy when R=0, or when the charge is an ideal point charge?
View SolutionElectric field in a region of space is radially outward from origin and varies with distance 'r' from origin as E = kr. Find the charge enclosed in a sphere of radius 'a' centred at origin.
View SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as `rho = rho _(0) ( 1- ( r )/®)`, where `rho_(0)` is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy `:` The field has a spherical symmetry . For a point outside the ball `( r gt R )`
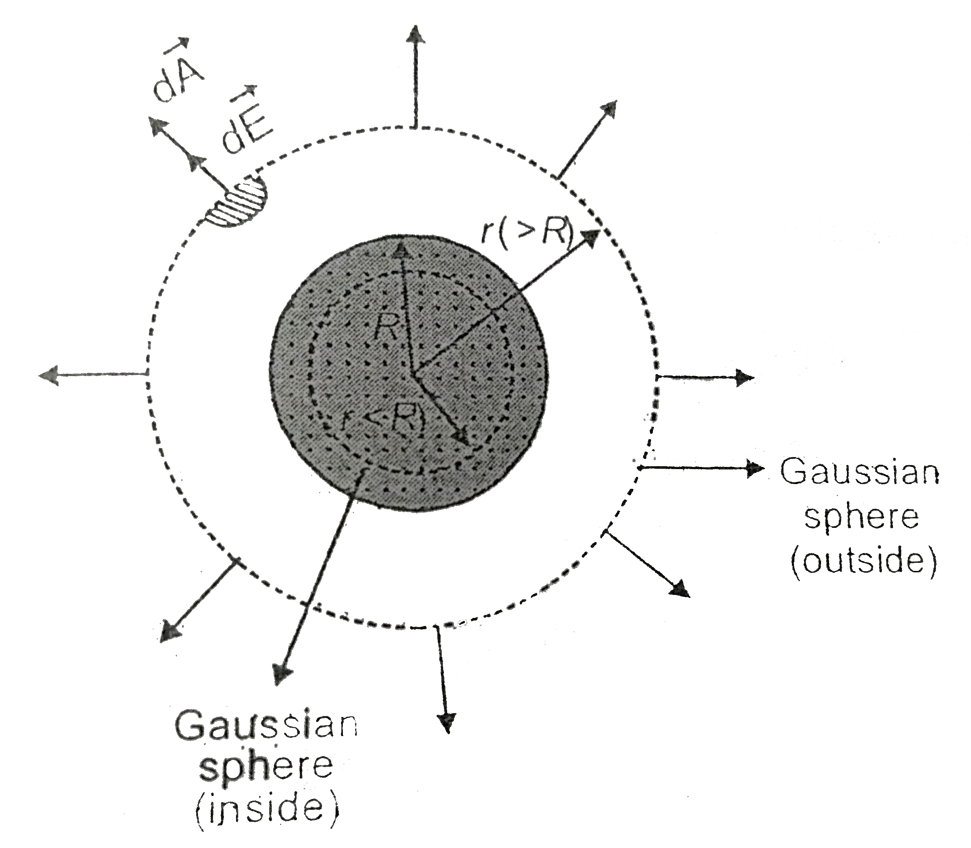
`phi =oint vec(E). bar(dA) = E xx 4 pi r^(2)`
By Gauss law , `phi= ( Q)/( epsilon_(0))`
`implies E_(out) = (Q)/( 4pi epsilon_(0)r^(2))`, where Q is total charge
For a point inside the ball ` ( r lt R )`
` phi = oint vec(E) . bar(dA) = E xx 4 pi r^(2)`
By Gauss law, `phi = ( q_(enc))/(epsilon_(0))`
`implies E_("in")= ( q_(enc))/( 4pi epsilon_(0)r^(2))`
where ` q_(enc)= ` charge in a sphere of radius `r ( lt R)`
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume `dV = 4pi r^(2) dr`
Charge `dq = rho dV`
`implies dq= rho _(0) (1-(r )/(R)) 4pi r^(2) dr`
`implies q= int _(0)^(r ) rho _(0) ( 1- (r)/( R )) 4pi r^(2) dr`
`= rho _(0)4pi [ int_(0)^(r ) r^(2) dr - int_(0)^(r ) (r^(3))/(R) dr ]= rho _(0) 4pi [ ( r^(3))/( 3) - (r^(4))/( 4R)]`

View SolutionA charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.

Strategy `:` The net electric field inside the conductor is zero. Thsi is produced by induced charges and the external charge.

View SolutionA point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad `R(lt r)`. The potential at any point on the sphere is
View SolutionA point charge `+q` is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionThere are two thin concentric conducting shells of radii a and `b(a lt b)` . Equal charges Q given to each shell. Find the charge distribution on the inner and outer shell.
View SolutionTwo charged metallic spheres of radii `r_(1)` and `r_(2)` are touched and separated . Calculate the ratio of their
(1) Charges
(2) Potential
(3) Self energy
(4) Electric field at the surface
(5) Surface charge density
View SolutionThere are three concentric shells or radii a,b and `c(a lt b lt c)` . Equal charges Q each are given to innermost and outermost shell . The middle shell is grounded. Determine the charge appearing on each surface of middle shell.
Strategy `:` When a conductor is grounded (i.e., connected to earth ) its potential becomes zero due to flow of charge either from shell or from ground.
View SolutionTwo conducting plates A and B are placed parallel to each other. A is given a charge. `Q_1` and B a charge `Q_2`. Find the distribution of charges on the four surface.
View SolutionThe distance between the two plates of a cathode-ray oscilloscope is 1 cm and the potential difference between them is 1200 V. If an electron of energy 2000 eV enters at right angles to the field, what will be its deflection if the plate be 1.5 cm long.
View SolutionUsing the concept of energy density , show that the total energy stored by a shell of radius R and charge Q is `(Q^(2))/( 8 pi epsilon_(0)R)`
View SolutionA charge Q is filled in a spherical volume of Radius R . Use the concept of energy density , find energy stored inside the charge volume.
View SolutionIn a solid uniformly charged sphere of total charge Q and radius R, if energy stored out side the sphere is `U_(0)` joules then find out self energy of sphere in term of `U_(0)` ?
View SolutionFind the charges on the three capacitors shown in figure
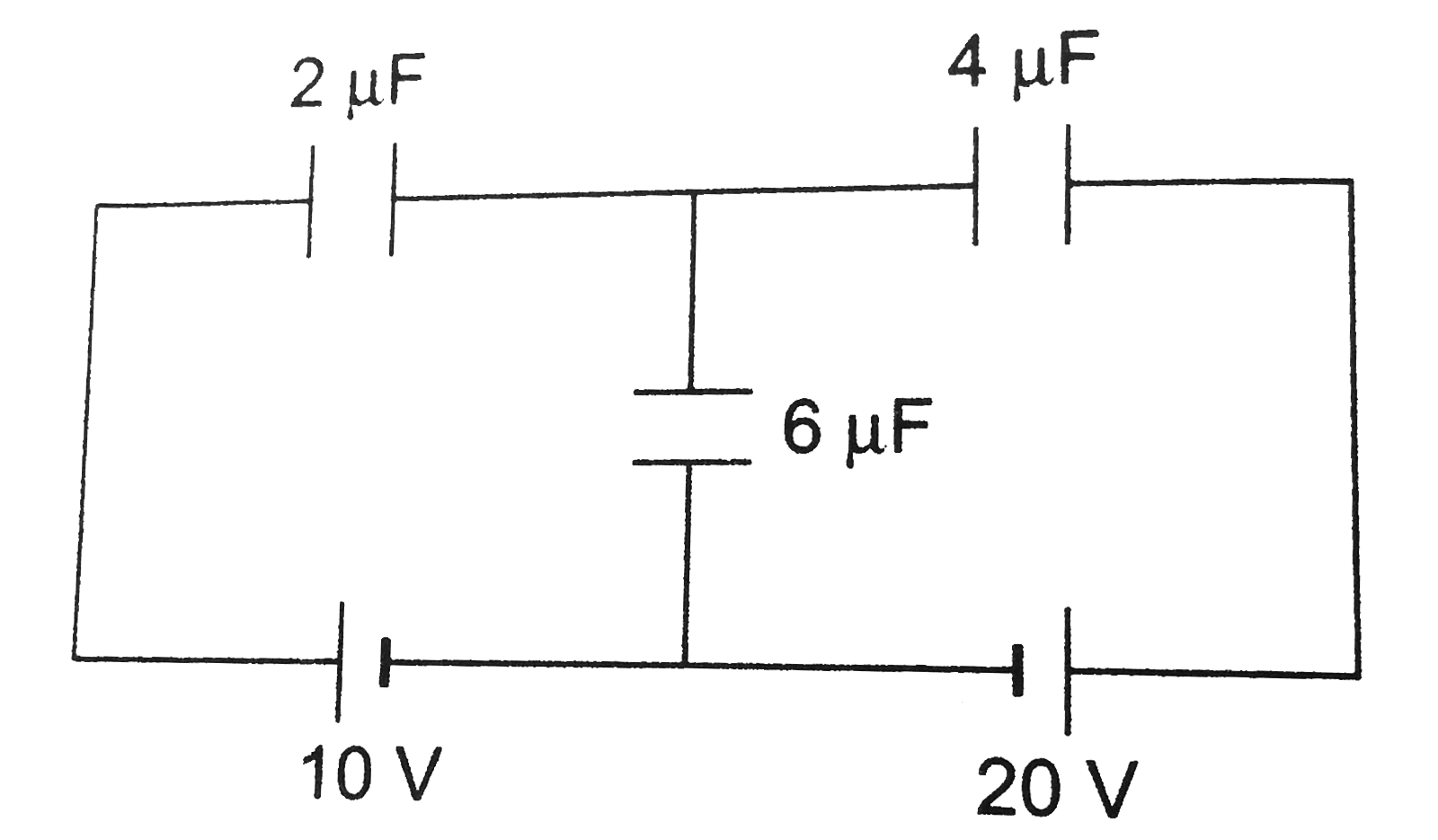
View SolutionFind the potential difference `V_(A)- V_(B)` between points A and B of the circuit shown in figure.
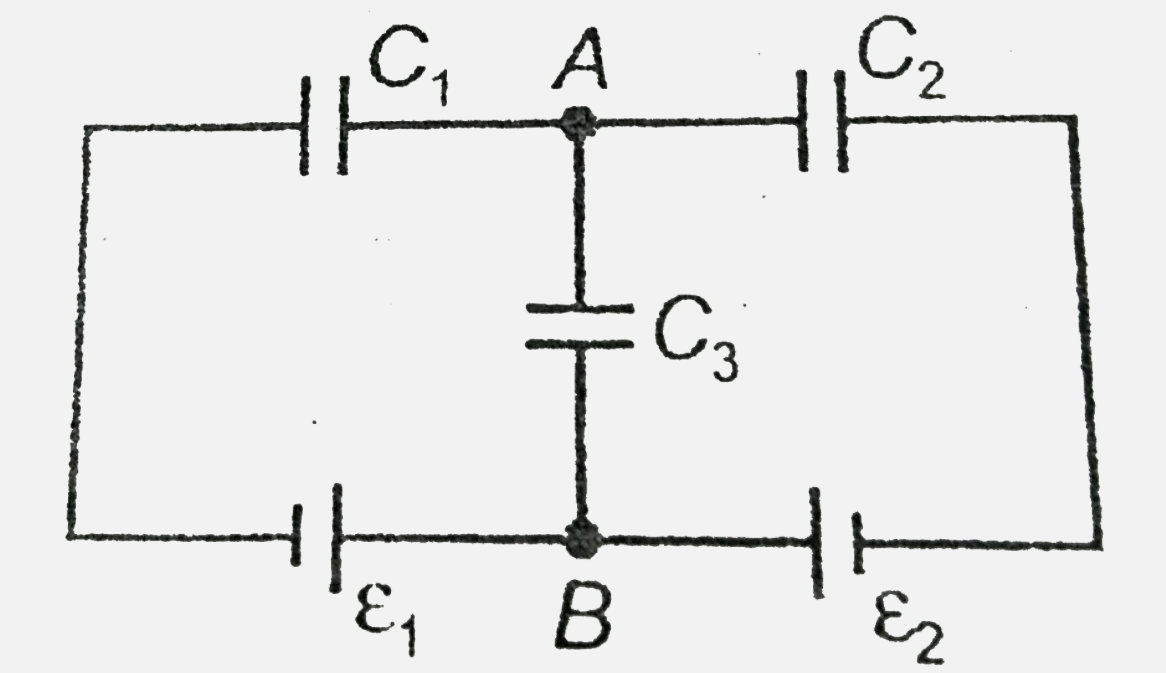
View SolutionDetermine the potential difference `V_(A)-V_(B)` between point A and B of the circuit shown in figure . Under what condition is it equal to zero ?
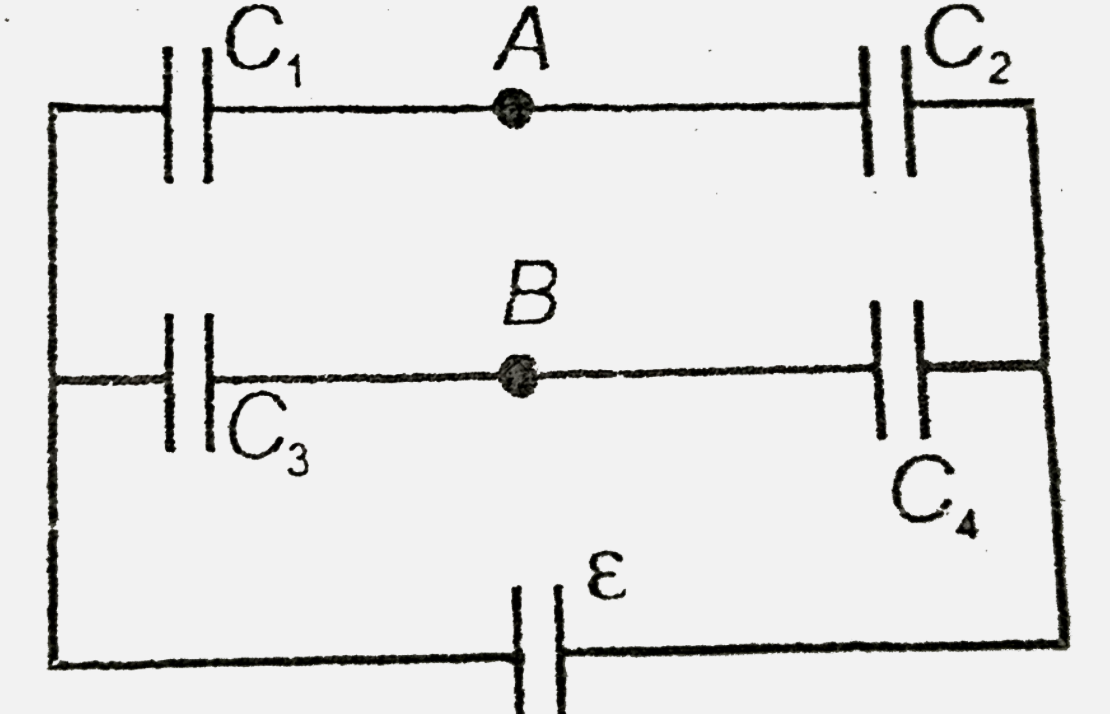
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J . What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View SolutionFind the change in electric potential energy , `Delta U` as a charge of (a) `2.20 xx 10^(-6) C.` (b) `- 1.10 xx 10^(-6) C ` moves from a point A to a point given that the change in electric potential between these points is `DeltaV= V_(B) -V_(A) = 24.0 V`
View SolutionA particle of mass m and positive charge q is released from point A. Its speed is found to be v when it passes through a point B. Which of the two points is at higher potential ? What is the potential difference between the points ?
View SolutionAn electron , with charge of `-1.60 xx 10^(19) C`, accelerates from rest through a potential difference V. A proton , with a charge of `+ 1.60 xx 10^(-19) C `, accelerates from rest through a potential difference `-V` . Is the final speed of the electron (a) more than , (b) less than , or (c ) same as the final speed of the proton ?
View SolutionA charge of 10C is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J. What is the potential difference `V_(A)-V_(B)`?
View SolutionSuppose the an electron in the picture tube of a televisoin set is accelerated from rest through a potential differnece `V_(b)-V_(a)= V_(ba) = +5000V`.
(a) What is the change in electric potential energy of the electron?
(b) What is the speed of the electron `( m = 9.1 xx 10^(-31) kg)` as a result of this acceleration ?
View SolutionDetermine the potential at a point 0.50 m (i) from a`+20 muC` potential charge (ii) from a`-20 muC` point charge.
View SolutionFigures (a) and (b) show the field lines of a positive and negative point charge respectively.

(a) Give the signs of the potential difference `V_(P)-V_(Q), V_(B)-V_(A)`.
(b) Give the sign of the potential energy difference of a small negative charge between the points Q and P, A and B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
(d) Give the sign of the work done by the external agency in moving a small negative charge from B to A.
(e) Does the kinetic energy of a small negative charge increase or decrease in going from B to A?
View SolutionThe classical method of a hydrogen atom in its normal, unexcited configuration has an electron that revolves around a proton at a distance of `5.3 xx 10^(11)m`.
(a) What is the electric potential due to the proton at the position of electron ?
(b) Determine the electrostatic potential energy between the two particles.
View SolutionWhat minimum work must be done by an external force to bring a charge `q=3.00 muC` from a great distance away (take `t = infty`) to a point `0.500 m` from a charge ` = 20.0 muC` ?
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin

(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .
View SolutionA charge `q_(1) = 2.00 mu C` is located at the origin , and a charge `q_(2) = - 6.00 mu C ` is located at `( 0,3.00 ) m`.
(a) Find the total electric potential due to these charges at the point `P` hose coordinates are ( 4.00,0) m .
( b) Find the change in potential energy of the system of two charges plus a charge `q_(3)= 3.00 muC` as the latter charge moves from infinity to point P .
View SolutionSuppose that three point charges `q_(a), q_(b)` and `q_(c)` are arranged at the vertices of a right -angled triangle as shown . What is the absolute electric potential at the position of the third charge if `q_(a)=- 6.0 mu C , q_(b)=+4.0muC , q_(c)=+2.0 mu C , a= 4.0 m ` and b=3.0 m ? Suppose that the third charge which is initially at rest is repelled to infinity by the combined electric field of the other two charges which are held fixed . What is the final final kinetic energy of the third charge ?
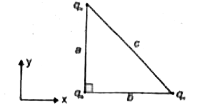
View SolutionTwo charges `3 xx 10^(-8) C` and `-2 xx 10^(-8)C` are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
View SolutionThere are four point charges placed at the vertices of a square of side, `a=1.4 m`. If `q_(1)=+18 nC,q_(2)=-24 nC,q_(3)+35nC and q_(4)=+16 nC`m then find the electric potential at the centre P of the square Assume the potential to be zero at infinity.

View SolutionTwo point charge - 5`mu`C and + 3`mu`C are placed 64 cm apart. At what points on the line joining the two charges is the electric potential zero. Assume the potential at infinity to be zero.
View SolutionIf `vec(E )` equals zero at a given point mus V equal for that point .
View SolutionIf you know ( E) at a given point, can you calculate V at that point ? If not, what further information do you need ?
View SolutionHow can you check whether the electric potential in a given region of space has constant value ?
View SolutionAn isolated conducting spherical shell carries a negative charge. What will happe if a positively charged metal object is placed in contact with the shell interior? Assume that the positive charge is (a) less than (b) equal to (c ) greater than the negative charge in magnitude.
View SolutionSome equipotential surfaces are shown in figure(29.E3) What can you say about the magnitude and the direction of the electric field?

View SolutionThe electric potential existing in space is `V(x,y,z)= A (xy+ yz+zx)`.(a) Write the dimensional formula of A. (b) find the expression for the electric field.( c ) If A is 10 SI units, find the magnitude of the electric field at (1m, 1m, 1m).
View SolutionAn electric field `E = (20 hat(i)+30 hat(j))` newton/coulomb exists in the space. If the potential at the origin is taken to be zero, find the potential at `(2m,2m)`.
View SolutionAn electric field `vec(E ) = hat(i) `Cx exists in the space, where C = 10 V/`m^(2)` . Taking the potential at (10 m, 20 m ) to be zero, find the potential at the origin.
View SolutionIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
View SolutionA spherical oil drop, radius `10^(-4)` cm has on it at a certain a total charge of 40 electrons. Calculate the energy that would be required to place an additional electron on the drop.
View SolutionA spherical drop of water carrying a charge of `3 xx 10^(-19)C` has a potential of 500 V at its surface. What is the radius of the drop ? If two drops of the same charge and the same radius combine to form a single spherical drop, what is the potential at the surface of the new drop ?
View SolutionA charge Q is distributed over two concentric conducting thin spherical shells radii r and R `(R gt 1)` . If the surface charge densities on the two shells are equal, the electric potential at the common centre is:

View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionTwo charges, `+q` and -q, each of mass m , are revolving in a circle of radius R, under mutual electrostatic force. Find (i) speed of each charge (ii) kinetic energy of system (iii) potential energy of the system (iv) total energy of the system.
View SolutionA proton is fixed at origin. Another proton is released from rest, from a point at a distance `r` from origin. Taking charge of portion as e and mass as `m`, find the speed of the proton (i) at a distance `2r` from origin (ii) at large distance from origin.
View SolutionThree charges are placed along x- axis at `x = -a , x=0` and `x=a` as shown . Calculate the potential energy of the system.

View SolutionCalculate the work required to be done to make an arrangement of three particles each having a charge `+q` such that the particles lie at the vertices of an equilateral triagnle of side a. What work will be doen by electric field when the particles are shifted away so that the side of triangle becomes 2a ?
View SolutionDetermine the interaction energy of the point charge located at the corners of a square with the side a in the circuits shown in figure.

View SolutionWhen an electric dipole is placed in a uniform electric field making angle `theta` with electric field, it experiences a torque `tau`. Calculate the minimum work donein changing the orientation to `2 theta`.
View SolutionA molecule of a substance has a permanent electric dipole moment of magnitude `10^(-30)` cm. A mole of this substance is polarised by applying a strong electrostatic field of magnitude `10^(7) V m^(-1).` The direction of field is charged by an angle `60^(@).` The heat released by the substance in aligning its dipole along the new direction of the field is
View SolutionTwo protons are separated by a distance R. What will be the speed of each proton when they reach infinity under their mutual repulsion?
View SolutionA bullet of mass 2 g is having a charge of 2 `mu`C. Through what potential difference must it be accelerated, starting from rest, to acquire a speed of 10 m/s ?
View SolutionThree equal charge Q are at the vertices of an equilateral triangle of side A. How much work is done (by an external angent ) in bringing them closser to an equilateral triangle of side A/2?
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of `+4.0 xx10^(-5) C.` They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View Solution
EXAMPLE questions and complete solutions for chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS ELECTROSTATIC POTENTIAL AND CAPACITANCE
- ASSIGNMENT (SECTION-A) Objective Type Questions (Only one answer)
- ASSIGNMENT SECTION - A
- ASSIGNMENT SECTION - B
- ASSIGNMENT SECTION - C
- ASSIGNMENT SECTION - D
- COMPREHENSION-II
- EXAMPLE
- EXERCISE
- SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
- SECTION-B(OBJECTIVE TYPE QUESTIONS(ONLY ONE ANSWER) )
- SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
- SECTION-D(COMPREHENSION-I)
- SECTION-E (Assertion-Reason Type Questios)
- SECTION-F(MATRIX-MATCH TYPE QUESTIONS)
- SECTION-G(INTEGER ANSWER TYPE QUESTIONS)
- SECTION-H Multiple True-False Type Questions
- SECTION-I Subjective Type Questions
- SECTION-J Aakash Challengers Questions
- TRY YOURSELF