Complete Solutions to Exercise (Single Option Correct Type Questions) of chapter VECTOR ALGEBRA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTOR ALGEBRA |
| ARIHANT MATHS | Exercise (Single Option Correct Type Questions) |
| Number Of Questions | 81 |
| Academic Year | 2023-24 |
If `a=3hati-2hatj+hatk,b=2hati-4hatj-3hatk and c=-hati+2hatj+2hatk`, then a+b+c is
View SolutionWhat should be added in vector `a=3hati+4hatj-2hatk` to get its resultant a unit vector `hati`?
View SolutionIf `a=2hati+2hatj-8hatk and b=hati+3hatj-4hatk`, then the magnitude of a+b is equal to
View SolutionIf `a=2hati+5hatj and b=2hati-hatj`, then the unit vector along a+b will be
View SolutionFind the unit vector parallel to the resultant vector of `2hati+4hatj-5hatk and hati+2hatj+3hatk`.
View SolutionIf `a=hati+2hatj+3hatk,b=-hati+2hatj+hatk and c=3hati+hatj`, then the unit vector along its resultant is
View SolutionIf `a=(2,5) and b=(1,4)`, then vector parallel to (a+b) is
View SolutionIn the `DeltaABC,AB=a,AC=c and BC=b`, then
View SolutionIf O is origin annd the position vector fo A is `4hati+5hatj`, then unit vector parallel to OA is
View SolutionThe position vectors of the points A,B and C are `hati+2hatj-hatk,hati+hatj+hatk and 2hati+3hatj+2hatk`, respectively. If A is chosen as the origin, then the position vectors of B and C are
View SolutionThe position vectors of `P and Q` are `5hati+4hatj+ahatk and -hati+2hatj-2hatk`, respectively. If the distance between them is 7, then find the value of `a`.
View SolutionIf position vector of points A,B and C are respectively `hati,hatj, and hatk` and `AB=CX`, then position vector of point X is
View SolutionThe position vectors of A and B are `2hati-9hatj-4hatk and 6hati-3hatj+8hatk` respectively, then the magnitude of AB is
View SolutionIf the position vectors of P and Q are `(hati+3hatj-7hatk) and (5hati-2hatj+4hatk)`, then |PQ| is
View SolutionIf the position vectors of P and Q are `hati+2hatj-7hatk and 5hati-2hatj+4hatk` respectively, the cosine of the angle between PQ and Z-axis is
View SolutionIf the position vectors of A and B are `hati+3hatj-7hatk and 5hati-2hatj+4hatk`, then the direction cosine of AB along Y-axis is
View SolutionThe direction cosines of vector `a=3hati+4hatj+5hatk` in the direction of positive axis of X, is
View SolutionThe direction cosines of the vector `3hati-4hatj+5hatk` are
View SolutionThe point having position vectors `2hati+3hatj+4hatk,3hati+4hatj+2hatk and 4hati+2hatj+3hatk` are the vertices of
View SolutionIf the position vectors of the vertices A,B and C of a `DeltaABC` are `7hatj+10k,-hati+6hatj+6hatk and -4hati+9hatj+6hatk`, respectively, the triangle is
View SolutionIf a,b and c are the position vectors of the vertices A,B and C of the `DeltaABC`, then the centroid of `DeltaABC` is
View SolutionIf a and b are position vector of two points A,B and C divides AB in ratio 2:1, then position vector of C is
View SolutionFind the position vector of the point which divides the join of the points `(2veca - 3vecb)` and `(3veca - 2vecb)` (i) internally and (ii) externally in the ratio `2 : 3` .
View SolutionIf O is origin and C is the mid - point of A (2, -1) and B ( -4, 3) . Then value of OC is
View SolutionIf the position vectors of the points A and B are `hati+3hatj-hatk and 3hati-hatj-3hatk`, then what will be the position vector of the mid-point of AB
View SolutionThe position vectors of A and B are `hati-hatj+2hatk and 3hati-hatj+3hatk`. The position vector of the middle points of the line AB is
View SolutionIf the vector `vecb` is collinear with the vector `vec a ( 2sqrt2,-1,4) `and `|vecb| =10`, then
View SolutionIf ` vec a , vec b` are the position vectors of the points `(1,-1),(-2,m),` find the value of `m` for which ` vec aa n d vec b` are collinear.
View SolutionThe points with position vectors `10hati+3hatj,12hati-5hatj and ahati+11hatj` are collinear, if a is equal to
View SolutionThe vectors `hati+2hatj+3hatk,lamdahati+4hatj+7hatk,-3hati-2hatj-5hatk` are collinear, of `lamda` is equal to (A)3 (B)4 (C)5 (D)6
View SolutionIf the points `a+b,a-b and a+kb` be collinear, then k is equal to
View SolutionIf the position vectors of A,B,C and D are `2hati+hatj,hati-3hatj,3hati+2hatj and hati+lamda hatj` respectively and `vec(AB) || vec(CD)`. Then `lamda` will be
View SolutionIf the vectors `3hati+2hatj-hatk and 6hati-4xhatj+yhatk` are parallel, then the value of x and y will be
View SolutionIf a and b are two non collinear vectors; then every vector r coplanar with a and b can be expressed in one and only one way as a linear combination: xa+yb=0.
View SolutionFour non-zero vectors will always be
View SolutionThe vectors a,b and a+b are
View SolutionFind the all the values of lamda such that `(x,y,z)!=(0,0,0)`and `x(hati+hatj+3hatk)+y(3hati-3hatj+hatk)+z(-4hati+5hatj)=lamda(xhati+yhatj+zhatk)`
View SolutionThe number of integral values of p for which `(p+1) hati-3hatj+phatk, phati + (p+1)hatj-3hatk` and `-3hati+phatj+(p+1)hatk` are linearly dependent vectors is q
View SolutionIf vectors `vec(AB) = -3hati+ 4hatk and vec(AC) = 5hati -2hatj+4hatk` are the sides of a `Delta ABC`, then the length of the median throught A is
View SolutionIn the figure, a vectors x satisfies the equation x+w=v. then, x is equal to
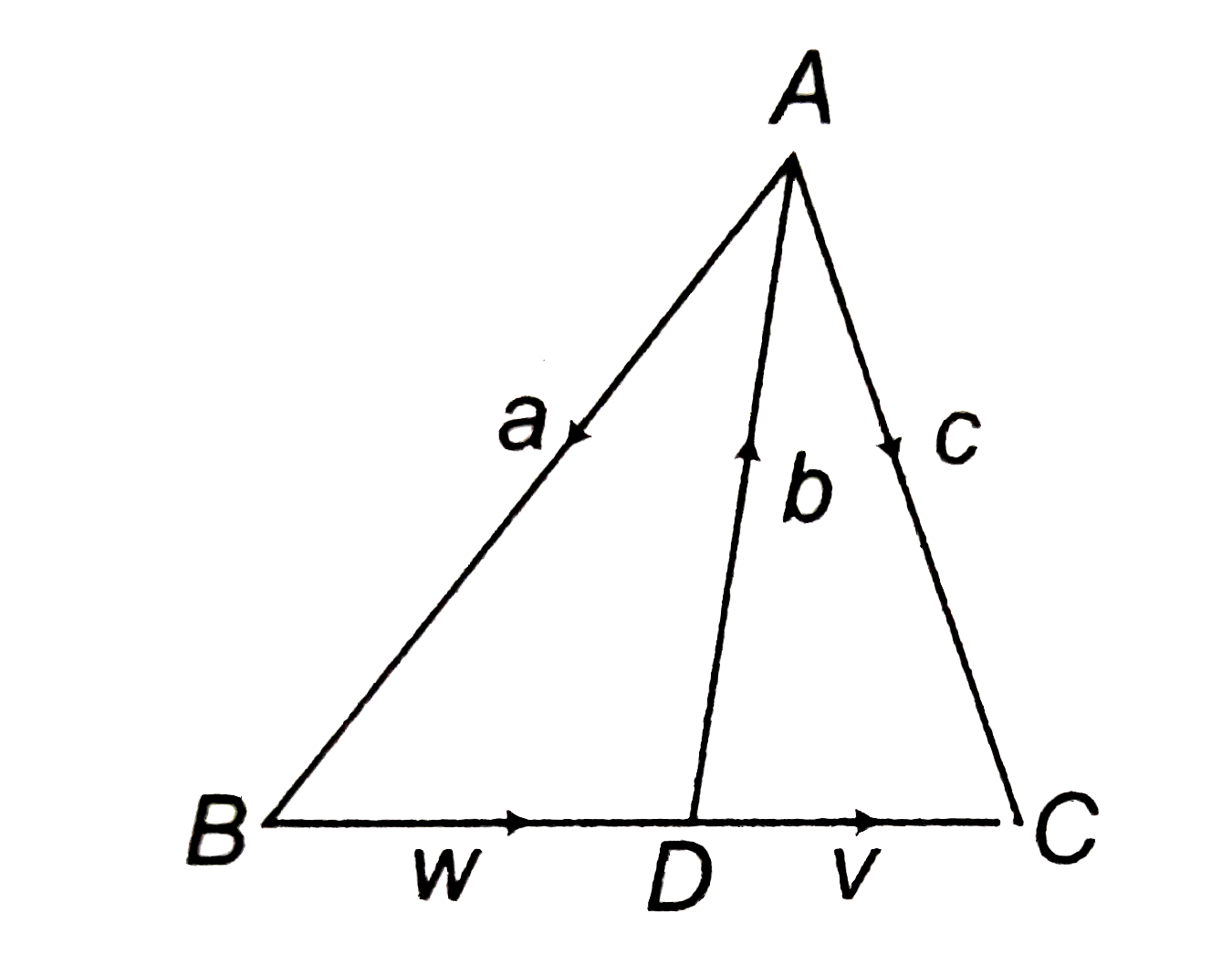
View SolutionVectors `veca = hati+2hatj+3hatk, vec b = 2hati-hatj+hatk and vecc= 3hati+hatj+4hatk` are so placed that the end point of one vector is the starting point of the next vector. Then the vectors are
View SolutionIf OP=8 and OP makes angles `45^(@) and 60^(@)` with OX-axis and OY-axis respectively, then OP is equal to
View SolutionLet a,b and c be three unit vectors such that `3a+4b+5c=0`. Then which of the following statements is true?
View Solutionif A,B,C,D and E are five coplanar points, then `vec(DA) + vec( DB) + vec(DC ) + vec( AE) + vec( BE) + vec( CE)` is equal to `:`
View SolutionIf the vectors `veca and vecb` are linearly independent satisfying `(sqrt3 tan theta+1) veca+ (sqrt3 sec theta -2)vecb =0`, then the most general values of `theta` are
View SolutionThe unit vector bisecting `vec(OY)` and `vec(OZ)` is
View SolutionA line passes through the points whose position vectors are `hati+hatj-2hatk` and `hati-3hatj+hatk`. The position vector of a point on it at unit distance from the first point is (A)`(1)/(5)(5hati+hatj-7hatk)` (B)`(1)/(5)(5hati+9hatj-13hatk)` (C)`(hati-4hatj+3hatk)` (D)`(1)/(5)(hati-4hatj+3hatk)`
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the `DeltaABC`, then `AD+BE+CF` is
View SolutionIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionIf the figure formed by the four points `hati+hatj-hatk,2hati+3hatj,3hati+5hatj-2hatk and hatk-hatj` is
View SolutionA and B are two points. The position vector of A is 6b-2a. A point P divides the line AB in the ratio 1:2. if a-b is the position vector of P, then the position vector of B is given by
View SolutionIf three points A,B and C are collinear, whose position vectors are `hati-2hatj-8hatk,5hati-2hatk and 11hati+3hatj+7hatk` respectively, then the ratio in which B divides AC is
View SolutionIf in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
View SolutionThe sides of a parallelogram are `2hati +4hatj -5hatk and hati + 2hatj +3hatk `. The unit vector parallel to one of the diagonals is
View SolutionIf A,B and C are the vertices of a triangle with position vectors `vec(a) , vec(b) ` and `vec(c )` respectively and G is the centroid of `Delta ABC`, then `vec( GA) + vec( GB ) + vec( GC )` is equal to
View SolutionConsider the regular hexagon ABCDEF with centre at O (origin).
Q. AD+EB+FC is equal to
View SolutionABCDE is a pentagon. Forces AB,AE,DC and ED act at a point. Which force should be added to this systemm to make the resultant 2AC?
View SolutionIn a regular hexagon ABCDEF, prove that AB+AC+AD+AE+AF=3AD.
View SolutionLet us define the length of a vector `ahati+bhatj+chatk` and `|a|+|b|+|c|`. This definition coincides with the usual definition of length of a vector `ahati+bhatj+chatk` if an only if
View SolutionIf a and b are two non-zero and non-collinear vectors then a+b and a-b are
View SolutionIf `|veca+ vecb| lt | veca- vecb|`, then the angle between `veca and vecb` can lie in the interval
View SolutionThe magnitudes of mutually perpendicular forces a,b and c are 2,10 and 11 respectively. Then the magnitude of its resultant is
View SolutionIf `hati-3hatj+5hatk` bisects the angle between `hata and -hati+2hatj+2hatk`, where `hata` is a unit vector, then
View SolutionLet `vec a= hat i` be a vector which makes an angle of `120^@` with a unit vector`vec b` in XY plane. then the unit vector `(vec a+ vec b)` is
View SolutionGiven three vectors ` vec a=6 hat i-3 hat j , vec b=2 hat i-6 hat ja n d vec c=-2 hat i+21 hat j` such that ` vecalpha= vec a+ vec b+ vec cdot` Then the resolution of the vector ` vecalpha` into components with respect to ` vec aa n d vec b` is given by a. `3 vec a-2 vec b` b. `3 vec b-2 vec a` c. `2 vec a-3 vec b` d. ` vec a-2 vec b`
View Solution`' I '` is the incentre of triangle `A B C` whose corresponding sides are `a , b ,c ,` rspectively. `a vec I A+b vec I B+c vec I C` is always equal to (a). ` vec0` ( b). `(a+b+c) vec B C` (c). `( vec a+ vec b+ vec c) vec A C` ( d). `(a+b+c) vec A B`
View SolutionIf `vecx and vecy` are two non-collinear vectors and ABC is a triangle with side lengths a, b and c satisfying `(20a - 15b) vecx + ( 15b - 12c) vecy+ (12c - 20 a) (vecx xx vecy) = vec0`, then triangle ABC is
View SolutionIf ` vec xa n d vec y` are two non-collinear vectors and a, b, and c represent the sides of a ` A B C` satisfying `(a-b) vec x+(b-c) vec y+(c-a)( vec x xx vec y)=0,` then ` A B C` is (where ` vec xxx vec y` is perpendicular to the plane of `xa n dy` ) a. an acute-angled triangle b. an obtuse-angled triangle c. a right-angled triangle d. a scalene triangle
View SolutionIf the resultant of two forces is equal in magnitude to one of the components and perpendicular to it direction, find the other components using the vector method.
View SolutionIf ` vec b` is a vector whose initial point divides the join of `5 hat i and 5 hat j` in the ratio `k :1` and whose terminal point is the origin and `| vec b|lt=sqrt(37),then , k` lies in the interval
a. `[-6,-1//6]`
b. `(-oo,-6]uu[-1//6,oo)`
c. `[0,6]`
d. none of these
View SolutionIf `4hati+ 7hatj+ 8hatk, 2hati+ 3hatj+ 4hatk and 2hati+ 5hatj+7hatk` are the position vectors of the vertices A, B and C, respectively, of triangle ABC, then the position vector of the point where the bisector of angle A meets BC is
View SolutionIf `veca and vecb` are two unit vectors and `theta` is the angle between them, then the unit vector along the angular bisector of `veca and vecb` will be given by
View SolutionA, B, C and D have position vectors `veca, vecb, vecc and vecd`, repectively, such that `veca-vecb = 2(vecd-vecc)`. Then
View SolutionOn the xy plane where O is the origin, given points, `A(1, 0), B(0, 1) and C(1, 1)`. Let `P, Q, and R` be moving points on the line `OA, OB, OC` respectively such that `overline(OP)=45t overline((OA)),overline(OQ)=60t overline((OB)),overline(OR)=(1-t) overline((OC))` with `t>0.` If the three points `P,Q and R` are collinear then the value of `t` is equal to
A `(1)/(106)`
B `(7)/(187)`
C `(1)/(100)`
D none of these
View SolutionIf `a +b+c = alphad, b+c+d=beta a and a, b, c` are non-coplanar, then the sum of `a +b+c+d =`
View SolutionThe position vectors of the points P and Q with respect to the origin O are `veca = hati + 3hatj-2hatk and vecb = 3hati -hatj -2hatk`, respectively. If M is a point on PQ, such that OM is the bisector of POQ, then `vec(OM)` is
View Solution`A B C D` is a quadrilateral. `E` is the point of intersection of the line joining the midpoints of the opposite sides. If `O` is any point and ` vec O A+ vec O B+ vec O C+ vec O D=x vec O E ,t h e nx` is equal to a. `3` b. `9` c. `7` d. `4`
View SolutionIn the `triangle OAB`, M is the midpoint of AB, C is a point on OM, such that `2 OC = CM`. X is a point on the side OB such that OX = 2XB. The line XC is produced to meet OA in Y. Then `(OY)/(YA)=`
View SolutionPoints X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS. The line XY cuts the line PR at Z. Then, PZ is
View SolutionFind the value of `lamda` so that the points P, Q, R and S on the sides OA, OB, OC and AB, respectively, of a regular tetrahedron OABC are coplanar. It is given that `(OP)/(OA) = (1)/(3), (OQ)/(OB) = (1)/(2), (OR)/(OC) = (1)/(3) and (OS)/(AB)= lamda`.
View SolutionOABCDE is a regular hexagon of side 2 units in the XY-plane in the first quadrant. O being the origin and OA taken along the x-axis. A point P is taken on a line parallel to the z-axis through the centre of the hexagon at a distance of 3 units from O in the positive Z direction. Then find vector `vec(AP)`.
View Solution
Exercise (Single Option Correct Type Questions) questions and complete solutions for chapter VECTOR ALGEBRA of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS VECTOR ALGEBRA
- Example
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions