Complete Solutions to Example of chapter VECTOR ALGEBRA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTOR ALGEBRA |
| ARIHANT MATHS | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Classify the following measures as scalars and vectors
(i) 20 m north-west
(ii) 10 newton
(iii) 30 km/h
(iv) 50m/s towards north
(v) `10^(-19)` coloumb
View SolutionRepresent graphically
(i) a displacement of 60 km, `40^(@)` east of north
(ii) A displacement of 50 km south-east.
View SolutionIn the following figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial
(iv) collinear but not equal .
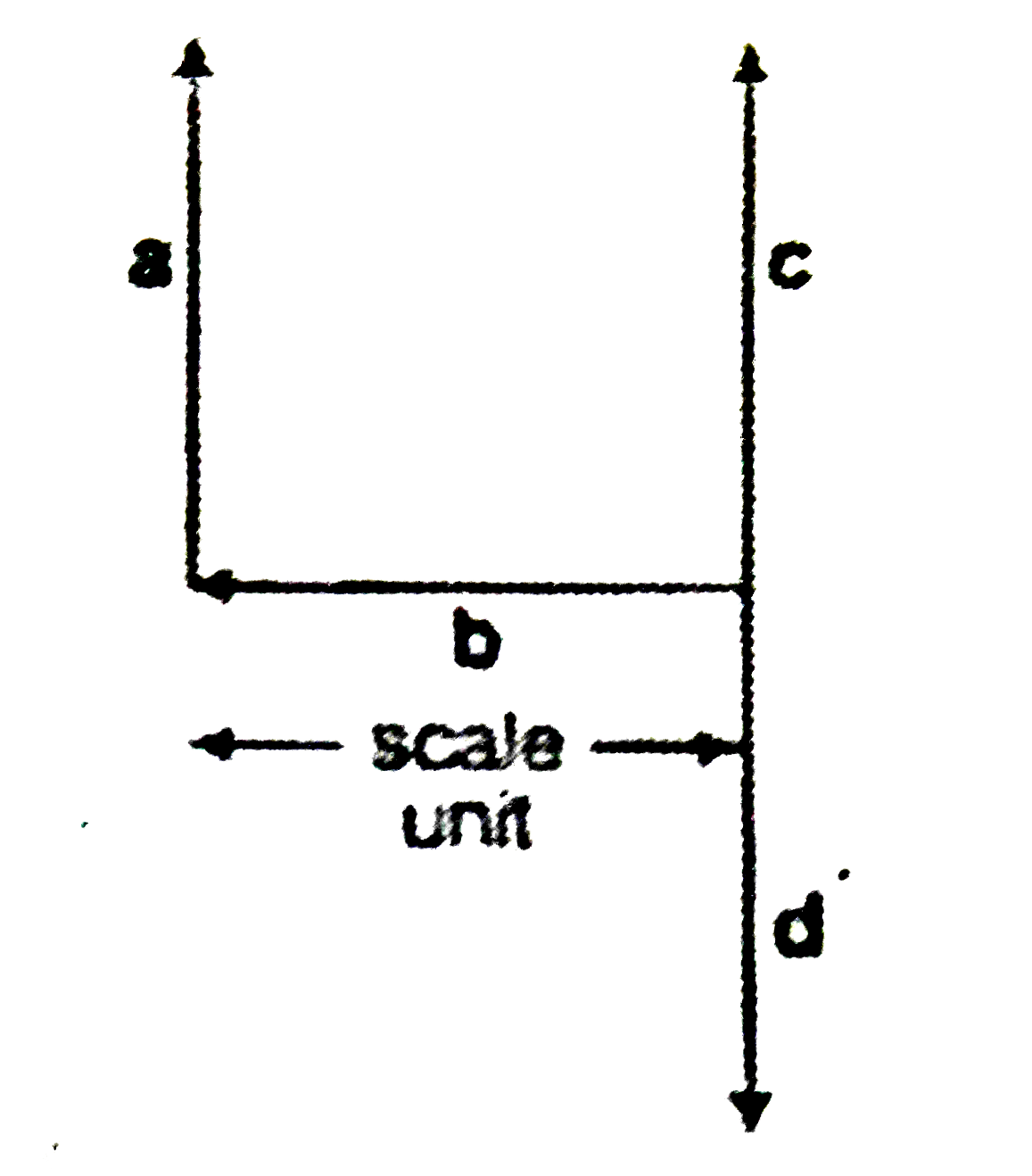
View SolutionFind a unit vector parallel to the vector `-3hati+4hatj`.
View SolutionLet `a=12hati+nhatj and |a|=13`, find th value of n.
View SolutionWrite two different vectors having same magnitude.
View SolutionIf one side of a squre be represented by the vectors `3hati+4hatj+5hatk`, then the area of the square is
View SolutionThe direction cosines of the vector `3hati-4hatj+5hatk` are
View SolutionShow that the vector `i+j+k` is equally inclined with the axes `O X ,\ O Y\ a n d\ O Zdot`
View SolutionLet AB be a vector in two dimensional plane with the magnitude 4 units and making an angle of `30^(@)` with X-axis and lying in the first quadrant. Find the components of AB along the two axes off coordinates. Hence, represent AB in terms of unit vectors `hati and hatj`.
View SolutionFind the unit vector parallel to the resultant vector of `2hati+4hatj-5hatk and hati+2hatj+3hatk`.
View SolutionIf ` vec a ,\ vec b ,\ vec c` be the vectors represented by theside sof a triangle, taken in order, then prove that ` vec a+ vec b+ vec c= vec0dot`
View SolutionIf S is the mid-point of side QR of a `DeltaPQR`, then prove that `PQ+PR=2PS`.
View SolutionIf ABCDEF is a regular hexagon, prove that `AD+EB+FC=4AB`.
View SolutionIf `A=(0,1)B=(1,0),C=(1,2),D=(2,1)` , prove that ` vec A B= vec C Ddot`
View SolutionIf the position vectors of A and B respectively `hati+3hatj-7hatk and 5 hati-2hatj+4hatk`, then find AB
View SolutionVectors drawn the origin `O` to the points `A , B and C` are respectively ` vec a , vec b and vec4a- vec3bdot` find ` vec A C and vec B Cdot`
View SolutionFind the direction cosines of the vector joining the points `A(1, 2, 3)`and`B(1, 2, 1)`, directed from A to B.
View SolutionLet `alpha, beta, gamma` be distinct real numbers. The points with position vectors `alpha hati + beta hatj +gamma hat k , beta hati + gamma hatj +alpha hat k , gamma hati +alpha hatj + beta hatk`
View SolutionIf the position vectors of the vertices of a triangle be `2hati+4hatj-hatk,4hati+5hatj+hatk and 3 hati+6hatj-3hatk`, then the triangle is
View SolutionThe sides of a parallelogram are `2hati +4hatj -5hatk and hati + 2hatj +3hatk `. The unit vector parallel to one of the diagonals is
View SolutionIf ` vec a , vec b` are any two vectors, then give the geometrical interpretation of relation `| vec a+ vec b|=| vec a- vec b|`
View SolutionIf the sum of two unit vectors is a unit vector, then the magnitude of their difference is
View SolutionIf `veca` is a non-zero vector of modulus a and m is a non-zero scalar, then `mveca` is a unit vector if
View SolutionFor a non-zero vector a, the set of real number, satisfying `|(5-x)a|lt|2a|` consists of all x such that
View SolutionFind a vector of magnitude (5/2) units which is parallel to the vector `3hati+4hatj`.
View SolutionIf `D`,`E` and `F` are the mid-points of the sides `BC`,`CA` and `AB` respectively of the `DeltaABC` and `O` be any point, then prove that `OA+OB+OC=OD+OE+OF`
View SolutionFind the position vectors of the points which divide the join of the points `2 vec a-3 vec ba n d3 vec a-2 vec b` internally and externally in the ratio `2:3` .
View SolutionThe position vectors of the vertices A,B and C of a triangle are `hati-hatj-3hatk,2hati+hatj-2hatk` and `-5hati+2hatj-6hatk`, respectively. The length of the bisector AD of the `angleBAC`, where D is on the segment BC, is
View SolutionThe median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.
View SolutionThe sum of the magnitudes of two forces acting at a point is 16 N. The resultant of these forces is perpendicular to the smaller force has a magnitude of 8 N. If the smaller force is magnitude x, then the value of x is (A) 2N (B) 4N (C) 6N (D) 7N
View SolutionThe length of longer diagonal of the parallelogram constructed on `5a + 2b` and `a-3b` . If it is given that `|a| = 2sqrt(2),|b|` = 3 and angle between a and b is `(pi)/(4)` is
View SolutionThe vector ` vec c `, directed along the internal bisector of the angle between the vectors `vec a = 7 hati - 4 hatj - 4hatk and vecb = -2hati - hatj + 2 hatk " with " |vec c| = 5 sqrt(6),` is
View SolutionShow that the vectors `2hati-3hatj+4hatk` and `-4hati+6hatj-8hatk` are collinear.
View SolutionProve that the ponts `A(1,2,3),B(3,4,7),C(-3 ,-2, -5)` are collinear and find the ratio in which B divides AC.
View SolutionIf the position vectors of A,B,C and D are
`2hati+hatj,hati-3hatj,3hati+2hatj and hati+lamda hatj` respectively and |AB||CD. Then `lamda` will be
View SolutionThe points with position vectors `60hati+3hatj,40hati-8hatj, ahati-52hatj` are collinear if (A) `a=-40` (B) `a=40` (C) `a=20` (D) none of these
View SolutionIf a,b and c are three non-zero vectors such that no two of these are collinear. If the vector a+2b is collinear with c and b+3c is collinear with a(`lamda` being some non-zero scalar), then a+2b+6c is equal to
View SolutionCheck whether the given three vectors are coplnar or non- coplanar :
`-2hati -2 hatj + 4hatk, -2hati + 4hatj -2hatk, 4hati - 2hatj - 2hatk`.
View SolutionIf the vectors `4hati+11hatj+mhatk,7hati+2hatj+6hatk and hati+5hatj+4hatk` are coplanar, then m is equal to
View SolutionIf a,b and c are non-coplanar vectors, prove that 3a-7b-4c, 3a-2b+c and a+b+2c are coplanar.
View SolutionThe value of `lamda` for which the four points `2hati+3hatj-hatk,hati+2hatj+3hatk,3hati+4hatj-2hatk` and `hati-lamdahatj+6hatk` are coplanar.
View SolutionShow that the points `P(a+2b+c),Q(a-b-c),R(3a+b+2c) and S(5a+3b+5c)` are coplanar given that a,b and c are non-coplanar.
View SolutionShow that the vectors
`hati-3hatj+2hatk,2hati-4hatj-hatk and 3hati+2hatj-hatk` and linearly independent.
View SolutionIf `veca=hati+hatj+hatk, vecb=4hati+3hatj+4hatk` and `vecc=hati+alphahatj+betahatk`
are linearly dependent vectors and `|vecc|=sqrt(3)` then:
View SolutionThe non-zero vectors are `vec a,vec b and vec c` are related by `vec a= 8vec b and vec c = -7vec b`. Then the angle between `vec a and vec c` is
View SolutionA unit vector `hata` makes an angle `pi/4` with z-axis, `if hata+hati+hatj` is a unit vector then `hata` is equal to
(A) `hati+hatj+hatk/2` (B) `hati/2+hatj/2-hatk/sqrt(2)` (C) `-hati/2-hat/2+hatk/sqrt(2)` (D) `hati/2-hatj/2-hatk/sqrt(2)`
View SolutionIf the resultannt of two forces of magnitudes P and Q acting at a point at an angle of `60^(@)` is `sqrt(7)Q`, then P/Q is
View SolutionThe vector ` vec a` has the components `2p` and 1 w.r.t. a rectangular Cartesian system. This system is rotated through a certain angel about the origin in the counterclockwise sense. If, with respect to a new system, ` vec a` has components `(p+1)a n d1` , then `p` is equal to a. `-4` b. `-1//3` c. `1` d. `2`
View SolutionABC is an isosceles triangle right angled at A. forces of magnitude `2sqrt(2),5 and 6` act along BC, CA and AB respectively. The magnitude of their resultant force is
View SolutionA line segment has length 63 and direction ratios
are `3, -2, 6.` The components of the line vector are
View SolutionIf the vectors `6hati-2hatj+3hatkk,2hati+3hatj-6hatk and 3hati+6hatj-2hatk` form a triangle, then it is
View SolutionThe position vectors of the points A, B, C are `2 hati + hatj - hatk , 3 hati - 2 hatj + hatk and hati + 4hatj - 3 hatk ` respectively . These points
View SolutionThe position vector of a point C with respect to B is `hat i +hat j` and that of B with respect to A is `hati-hatj`. The position vector of C with respect to A is
View SolutionIn a `DeltaABC`, if 2AC=3CB, then 2OA+3OB is equal to
View SolutionIf ` vec a` ,` vec b` ,` vec c` ,` vec d` are the position vector of point `A , B , C` and `D` , respectively referred to the same origin `O` such that no three of these point are collinear and ` vec a` + ` vec c` = ` vec b` + ` vec d` , than prove that quadrilateral `A B C D` is a parallelogram.
View SolutionP is a point on the side BC off the `DeltaABC` and Q is a point such that PQ is the resultant of AP,PB and PC. Then, ABQC is a
View SolutionIf ABCD is a parallelogram and the position vectors of A,B and C are `hati+3hatj+5hatk, hati+hatj+hatk and 7 hati+7hatj+7hatk`, then the poisitionn vector of D will be
View Solution`ABCD` is a parallelogram whose diagonals meet at P. If O is a fixed point, then `vec(OA)+vec(OB)+vec(OC)+vec(OD)` equals :
View SolutionIf C is the middle point of AB and P is any point outside AB, then
View SolutionLet O, O' and G be the circumcentre, orthocentre and centroid of a `Delta ABC` and S be any point in the plane of the triangle.
Statement -1: `vec(O'A) + vec(O'B) + vec(O'C)=2vec(O'O)`
Statement -2: `vec(SA) + vec(SB) + vec(SC) = 3 vec(SG)`
View SolutionFive points given by A,B,C,D and E are in a plane. Three forces AC,AD and AE act at A annd three forces CB,DB and EB act B. then, their resultant is
View SolutionIn a regular hexagon `A B C D E F ,\ A vec B=a ,\ B vec C= vec b\ a n d\ vec C D=cdotT h e n\ vec A E=` ` vec a+ vec b+ vec c` b. `2 vec a+ vec b+ vec c` c. ` vec b+ vec c` d. ` vec a+2 vec b+2 vec c`
View SolutionIf `veca+vecb+vecc=vec0, |veca| = 3, |vecb| = 5, |vecc| = 7`, then angle between `veca` and `vecb` is : a. `(pi)/(2)` b. `(pi)/(3)` c. `(pi)/4` d. `(pi)/(6)`
View SolutionIf `veca` & `vecb` are the position vectors of `A` & `B` respectively and `C` is a point on `AB` produced such that `AC=3AB` then the position vector of `C` is:
View SolutionLet `A` and `B` be points with position vectors `veca` and `vecb` with respect to origin `O`. If the point `C` on `OA` is such that `2vec(AC)=vec(CO), vec(CD) ` is parallel to `vec(OB)` and `|vec(CD)|=3|vec(OB)|` then `vec(AD)` is (A) `vecb-veca/9` (B) `3vecb-veca/3` (C) `vecb-veca/3` (D) `vecb+veca/3`
View SolutionIf the position vector of a point A is `vec a + 2 vec b and vec a ` divides AB in the ratio `2:3`, then the position vector of B, is
View SolutionIf D, E and F are respectively, the mid-points of AB, AC and BC in `DeltaABC`, then BE + AF is equal to
View SolutionIn a quadrilateral `P Q R S , vec P Q= vec a , vec Q R = vec b , vec S P= vec a- vec b ,M` is the midpoint of ` vec Q Ra n dX` is a point on `S M` such that `S X=4/5S Mdot` Prove that `P ,Xa n dR` are collinear.
View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If `vec(OA)=veca, vec(OB)=vecb, vec(OC)=vecc`, then `vec(AB)+2vec(BC)+3vec(CA)=`
View SolutionIf `veca, vecb` and `vecc` are position vectors of A,B, and C respectively of `DeltaABC` and `if|veca-vecb|,|vecb-vec(c)|=2, |vecc-veca|=3`, then the distance between the centroid and incenter of `triangleABC` is
View SolutionLet position vectors of point A,B and C of triangle ABC represents be `hati+hatj+2hatk, hati+2hatj+hatk` and `2hati+hatj+hatk`. Let `l_(1),l_(2)` and `l_(3)` be the length of perpendicular drawn from the orthocenter 'O' on the sides AB, BC and CA, then `(l_(1)+l_(2)+l_(3))` equals
View SolutionABCDEF is a regular hexagon in the x-y plance with vertices in the anticlockwise direction. If `vecAB=2hati`, then `vecCD` is
View SolutionThe vertices of a triangle are A(1,1,2), B (4,3,1) and C (2,3,5). The vector representing internal bisector of the angle A is
View SolutionLet `veca=(1,1,-1), vecb=(5,-3,-3)` and `vecc=(3,-1,2)`. If `vecr` is collinear with `vecc` and has length `(|veca+vecb|)/(2)`, then `vecr` equals
View SolutionIn a trapezium ABCD the vector `B vec C = lambda vec(AD).` If `vec p = A vec C + vec(BD)` is coillinear with `vec(AD)` such that `vec p = mu vec (AD),` then
View SolutionIf the position vectors of the points A,B and C be `hati+hatj,hati-hatj` and `ahati+bhatj+chatk` respectively, then the points A,B and C are collinear, if
View SolutionLet a,b and c be distinct non-negative numbers and the vectors `ahati+ahatj+chatk,hati+hatk,chati+chatj+bhatk` lie in a plane, then the quadratic equation `ax^(2)+2cx+b=0` has
View SolutionThe number of distinct real values of `lamda` for which the vectors `veca=lamda^(3)hati+hatk, vecb=hati-lamda^(3)hatj` and `vecc=hati+(2lamda-sin lamda)hatj-lamdahatk` are coplanar is
View SolutionThe points `A(2-x,2,2), B(2,2-y,2), C(2,2,2-z)` and `D(1,1,1)` are coplanar, then locus of `P(x,y,z)` is
View Solution`p=2a-3b,q=a-2b+c` and `r=-3a+b+2c`, where `a,b,c` being non-coplanar vectors, then the vector `-2a+3b-c` is equal to
View SolutionIf `a_(1)` and `a_(2)` are two values of a for which the unit vector `aveci + bvecj +1/2veck` is linearly dependent with `veci+2vecj` and `vecj-2veck`, then `1/a_(1)+1/a_(2)` is equal to
View SolutionThe vector `hati +xhatj+3hatk` is rotated through an angle `theta` and is doubled in magnitude. It now becomes `4hati+ (4x-2)hatj +2hatk`. The values of x are
View Solution` vec a , vec b , vec c` are three coplanar unit vectors such that ` vec a+ vec b+ vec c=0.` If three vectors ` vec p , vec q ,a n d vec r` are parallel to ` vec a , vec b ,a n d vec c ,` respectively, and have integral but different magnitudes, then among the following options, `| vec p+ vec q+ vec r|` can take a value equal to a. `1` b. `0` c. `sqrt(3)` d. `2`
View SolutionA,B C and dD are four points such that `vec (AB) = m(2 hati - 6 hatj + 2hatk) vec(BC) = (hati - 2hatj) and vec(CD) = n (-6 hati + 15 hatj - 3 hatk)`. If CD intersects AB at some points E, then
View SolutionIf non-zero vectors `veca and vecb` are equally inclined to coplanar vector `vecc`, then `vecc` can be
View SolutionThe vectors `x hati + (x+1)hatj + (x+2)hatk, (x+3)hati+ (x+4)hatj + (x+5)hatk and (x+6)hati + (x+7)hatj+ (x+8)hatk` are coplanar if x is equal to a. 1 b. -3 c. 4 d. 0
View SolutionGiven three vectors `veca, vecb` and `vecc` are non-zero and non-coplanar vectors. Then which of the following are coplanar.
View SolutionIn a four-dimensional space where unit vectors along the axes are `hati,hatj,hatk and hatl, and a_(1),a_(2),a_(3),a_(4) ` are four non-zero vectors such that no vector can be expressed as a linear combination of other `(lamda-1) (a_(1)-a_(2))+mu(a_(2)+a_(3))+gamma(a_(3)+a_(4)-2a_(2))+a_(3)+deltaa_(4)=0`, then
View SolutionStatement 1: `| vec a|=3,| vec b|=a n d| vec a+ vec b|=5,t h e n| vec a- vec b|=5.` Statement 2: The length of the diagonals of a rectangle is the same.
View SolutionStatement 1: If `| vec a+ vec b|=| vec a- vec b|,t h e n vec aa n d vec b` are perpendicular to each other. Statement 2: If the diagonal of a parallelogram are equal magnitude, then the parallelogram is a rectangle.
View SolutionAssertion: If I is the incentre of `/_\ABC, then`|vec(BC)| vec(IA) +|vec(CA)| vec(IB) +|vec(AB)| vec(IC) =0` Reason: If O is the origin, then the position vector of centroid of `/_\ABC` is (vec(OA)+vec(OB)+vec(OC))/3`
View SolutionStatement 1: If ` vec ua n d vec v` are unit vectors inclined at an angle `alphaa n d vec x` is a unit vector bisecting the angle between them, then ` vec x=( vec u+ vec v)//(2sin(alpha//2)dot` Statement 2: If `"Delta"A B C` is an isosceles triangle with `A B=A C=1,` then the vector representing the bisector of angel `A` is given by ` vec A D=( vec A B+ vec A C)//2.`
View SolutionStatement I: If `a=2hati+hatk,b=3hatj+4hatk and c=lamda a+mub` are coplanar, then `c=4a-b`.
Statement II: A set vector `a_(1),a_(2),a_(3), . . ,a_(n)` is said to be linearly independent, if every relation of the form
`l_(1)a_(1)+l_(2)a_(2)+l_(3)a_(3)+ . . .+l_(n)a_(n)=0` implies that `l_(1)=l_(2)=l_(3)= . . .=l_(n)=0` (scalar).
View SolutionStatement 1 : Let `A(veca), B(vecb) and C(vecc)` be three points such that `veca = 2hati +hatk , veb = 3hati -hatj +3hatk and vecc =-hati +7hatj -5hatk`. Then OABC is tetrahedron.
Statement 2 : Let `A(veca) , B(vecb) and C(vecc)` be three points such that vectors `veca, vecb and vecc` are non-coplanar. Then OABC is a tetrahedron, where O is the origin.
View SolutionStatement 1: Let ` vec a , vec b , vec ca n d vec d` be the position vectors of four points `A ,B ,Ca n dD` and `3 vec a-2 vec b+5 vec c-6 vec d=0.` Then points `A ,B ,C ,a n dD` are coplanar. Statement 2: Three non-zero, linearly dependent coinitial vector `( vec P Q , vec P Ra n d vec P S)` are coplanar. Then ` vec P Q=lambda vec P R+mu vec P S ,w h e r elambdaa n dmu` are scalars.
View SolutionGiven that p(3,2,-4) , Q (5,4, -6) and R (9,8,-10) are collinear find the ratio in which Q divides PR
View SolutionGiven that p(1,2,-4) , Q (5,4, -6) and R (0,8,-10) are collinear find the ratio in which Q divides PR
View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio `1:2`. AL intersects BD at P.M is a point on DC which divides DC in the ratio `1 : 2` and AM intersects BD in Q.
`PQ : DB` is equal to
View SolutionLet A,B,C,D,E represent vertices of a regular pentangon ABCDE. Given the position vector of these vertices be a,a+b,b,`lamda a` and `lamdab` respectively.
Q. AD divides EC in the ratio
View Solution
Example questions and complete solutions for chapter VECTOR ALGEBRA of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS VECTOR ALGEBRA
- Example
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions