Complete Solutions to Exercise (Comprehension) of chapter RELATIONS AND FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| CENGAGE NEW | Exercise (Comprehension) |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Consider the functions
`f(x)={(x+1",",x le 1),(2x+1",",1lt x le 2):} and g(x)={(x^(2)",", -1 le x lt2),(x+2",",2le x le 3):}`
The domain of the function `f(g(x))` is07:13View SolutionConsider the functions
`f(x)={(x+1",",x le 1),(2x+1",",1lt x le 2):} and g(x)={(x^(2)",", -1 le x lt2),(x+2",",2le x le 3):}`
The range of the function `f(g(x))` is05:41View SolutionIf the function `f(x)={(x+1",",x le 1),(2x+1",",1lt x le 2):} and g(x)={(x^(2)",", -1 le x lt2),(x+2",",2le x le 3):}` then the number of roots of the equation `f(g(x))=2`
04:35View SolutionConsider the function `f(x)` satisfying the identity `f(x) +f((x-1)/(x))=1+x AA x in R -{0,1}, and g(x)=2f(x)-x+1.`
The domain of `y=sqrt(g(x))` is07:00View SolutionConsider the function `f(x)` satisfying the identity `f(x) +f((x-1)/(x))=1+x AA x in R -{0,1}, and g(x)=2f(x)-x+1.`
The number of roots of the equation `g(x)=1` is05:21View SolutionConsider the function f(x) satisfyig the identity `f(x)+f((x-1)/x)=1+x, AA x in R-{0,1}` and `g(x)=2f(x)-x+1`
05:21View SolutionIf `(f(x))^2+f((1-x)/(1+x))=64 x AA in D_f` then
View SolutionIf `(f(x))^(2)xxf((1-x)/(1+x))=64x AAx in D_(f),` then
The domain of `f(x)` isView SolutionIf `(f(x))^(2)xxf((1-x)/(1+x))=64x AAx in D_(f),` then
The value of `f(9//7)` is07:44View Solution`f(x)={(x-1",",-1 le x le 0),(x^(2)",",0le x le 1):} and g(x)=sinx`
Consider the functions `h_(1)(x)=f(|g(x)|) and h_(2)(x)=|f(g(x))|.`
Which of the following is not true about `h_(1)(x)`?04:31View Solution`f(x)={(x-1",",-1 le x le 0),(x^(2)",",0le x le 1):} and g(x)=sinx`
Consider the functions `h_(1)(x)=f(|g(x)|) and h_(2)(x)=|f(g(x))|.`
Which of the following is not true about `h_(2)(x)`?05:54View Solution`f(x)={(x-1",",-1 le x le 0),(x^(2)",",0le x le 1):} and g(x)=sinx`
Consider the functions `h_(1)(x)=f(|g(x)|) and h_(2)(x)=|f(g(x))|.`
If for `h_(1)(x) and h_(2)(x)` are identical functions, then which of the following is not true?05:42View SolutionIf `a_0 = x,a_(n+1)= f(a_n)`, where `n = 0, 1, 2, ...,` then answer thefollowing questions. If `f (x) = msqrt(a-x^m),x lt0,m leq 2,m in N`,then
03:16View SolutionIf `a_(0)=x,a_(n+1)=f(a_(n)), " where " n=0,1,2, …,` then answer the following questions.
If `f(x)=(1)/(1-x),` then which of the following is not true?03:14View SolutionIf `a_(0)=x,a_(n+1)=f(a_(n)), " where " n=0,1,2, …,` then answer the following questions.
If `f:R to R ` is given by `f(x)=3+4x and a_(n)=A+Bx,` then which of the following is not true?04:00View SolutionLet `f(x)=f_1(x)-2f_2 (x)`, where ,where `f_1(x)={((min{x^2,|x|},|x|le 1),(max{x^2,|x|},|x| le 1))` and `f_2(x)={((min{x^2,|x|},|x| lt 1),({x^2,|x|},|x| le 1))` and let `g(x)={ ((min{f(t):-3letlex,-3 le x le 0}),(max{f(t):0 le t le x,0 le x le 3}))` for `-3 le x le -1` the range of `g(x)` is
06:47View SolutionLet `f(x)=f_(1)(x)-2f_(2)(x),` where
where `f(x)={(min{x^(2)","|x|}",",|x| le 1),(max{x^(2)","|x|}",",|x| gt 1):}`
and `f_(2)(x)={(min{x^(2)","|x|}",",|x| gt 1),(max{x^(2)","|x|}",",|x| le 1):}`
and let `g(x)={(min{f(t):-3 le t le x", "-3 le x lt 0}),(max{f(t): 0le t le x", " 0 le x le 3}):}`
For ` x in (-1,0), f(x)+g(x)` isView SolutionLet `f(x)=f_(1)(x)-2f_(2)(x),` where
where `f(x)={(min{x^(2)","|x|}",",|x| le 1),(max{x^(2)","|x|}",",|x| gt 1):}`
and `f_(2)(x)={(min{x^(2)","|x|}",",|x| gt 1),(max{x^(2)","|x|}",",|x| le 1):}`
and let `g(x)={(min{f(t):-3 le t le x", "-3 le x lt 0}),(max{f(t): 0le t le x", " 0 le x le 3}):}`
For `-3 le x le -1,` the range of g(x) is06:47View SolutionLet `f(x)={(2x+a",",x ge -1),(bx^(2)+3",",x lt -1):}`
and `g(x)={(x+4",",0 le x le 4),(-3x-2",",-2 lt x lt 0):}`
`g(f(x))` is not defined ifView SolutionLet `f(x)={(2x+a",",x ge -1),(bx^(2)+3",",x lt -1):}`
and `g(x)={(x+4",",0 le x le 4),(-3x-2",",-2 lt x lt 0):}`
If the domain of `g(f(x))" is " [-1, 4],` thenView SolutionLet `f(x)={(2x+a",",x ge -1),(bx^(2)+3",",x lt -1):}`
and `g(x)={(x+4",",0 le x le 4),(-3x-2",",-2 lt x lt 0):}`
If `a=2 and b=3,` then the range of `g(f(x))` isView SolutionLet `f : R -> R` is a function satisfying `f(2-x) = f(2 + x) and f(20-x)=f(x),AA x in R`. On the basis of above information, answer the following questions If `f(0)=5`, then minimum possible number of values of x satisfying `f(x) = 5`, for `x in [10, 170]` is
03:13View SolutionLet `f:R to R ` be a function satisfying `f(2-x)=f(2+x) and f(20-x)=f(x) AA x in R.` For this function `f`, answer the following.
The graph of `y= f(x)` is not symmetrial aboutView SolutionLet `f:R to R ` be a function satisfying `f(2-x)=f(2+x) and f(20-x)=f(x) AA x in R.` For this function `f`, answer the following.
If `f(2) ne f(6),` then the03:28View SolutionConsider two functions
`f(x)={([x]",",-2le x le -1),(|x|+1",",-1 lt x le 2):} and g(x)={([x]",",-pi le x lt 0),(sinx",",0le x le pi):}`
where [.] denotes the greatest integer function.
The number of integral points in the range of `g(f(x))` is06:28View SolutionConsider two functions
`f(x)={([x]",",-2le x le -1),(|x|+1",",-1 lt x le 2):} and g(x)={([x]",",-pi le x lt 0),(sinx",",0le x le pi):}`
where [.] denotes the greatest integer function.
The exhaustive domain of `g(f(x))` is06:28View SolutionConsider two functions
`f(x)={([x]",",-2le x le -1),(|x|+1",",-1 lt x le 2):} and g(x)={([x]",",-pi le x lt 0),(sinx",",0le x le pi):}`
where [.] denotes the greatest integer function.
The exhaustive domain of `g(f(x))` is06:28View SolutionConsider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
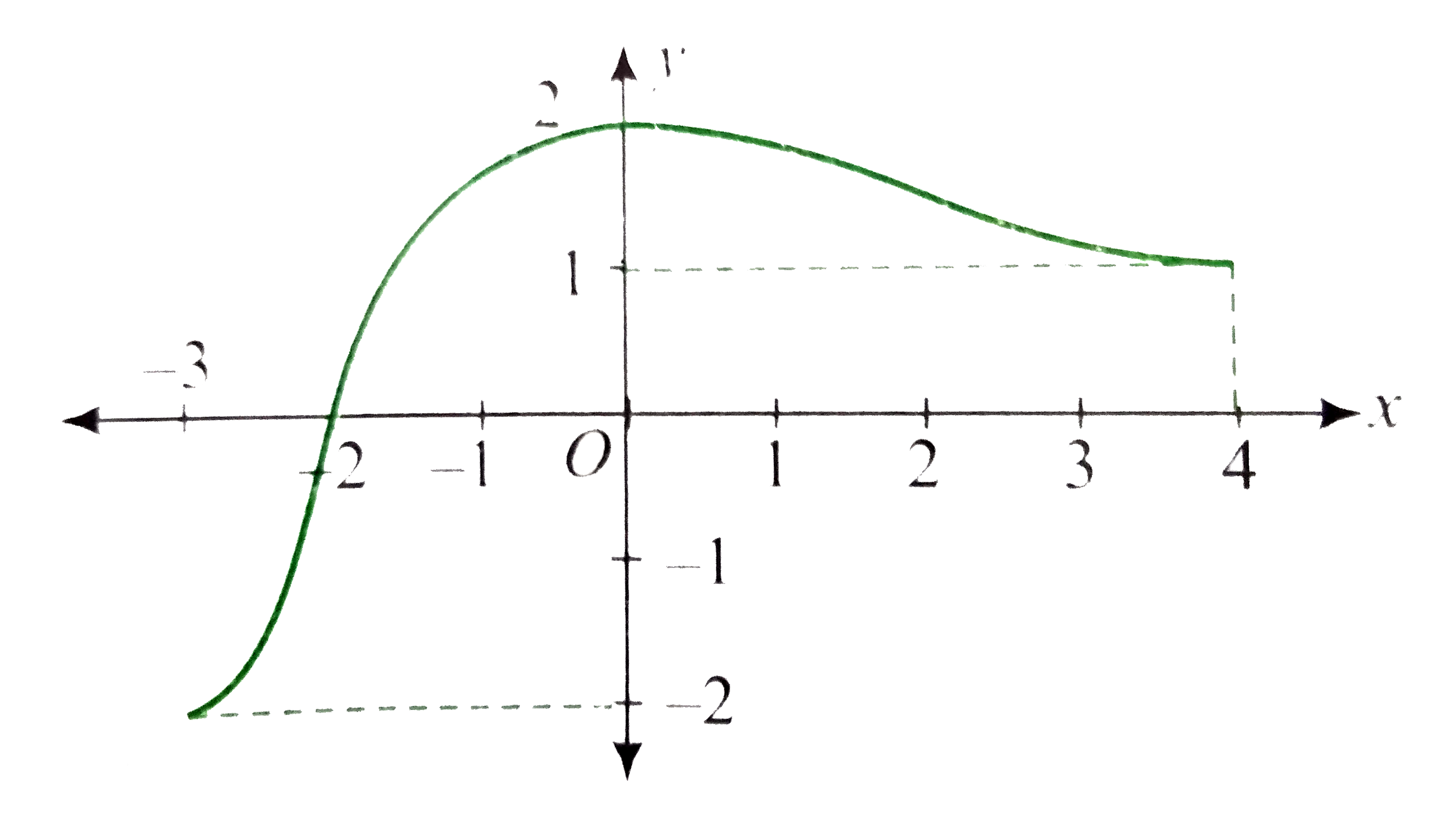
Domain and range of `g(x)=f(|x|)` is [a, b] and [c, d] respectively, then `(b-a+c+d)` is04:30View SolutionConsider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
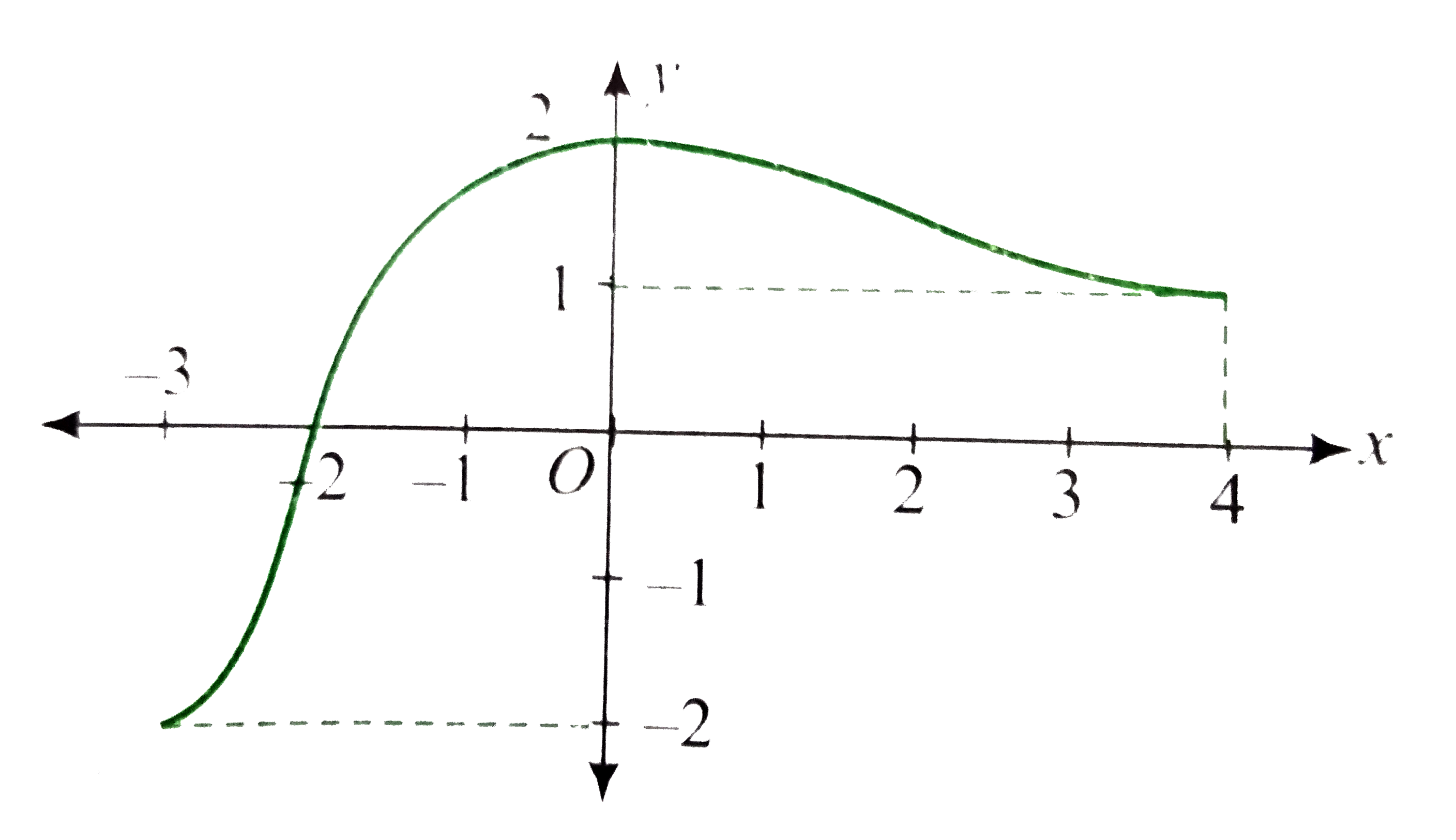
If `h(x)=|f(x)-(3)/(2)|` has range [e, f] and n be number of real solutions of `h(x)=(1)/(4), " then " (n+e+2f)` is08:48View SolutionConsider a differentiable `f:R to R` for which `f(1)=2 and f(x+y)=2^(x)f(y)+4^(y)f(x) AA x , y in R.`
The value of f(4) is04:27View SolutionConsider a differentiable `f:R to R` for which `f(1)=2 and f(x+y)=2^(x)f(y)+4^(y)f(x) AA x , y in R.`
The minimum value of `f(x)` is04:10View SolutionConsider a differentiable `f:R to R` for which `f(1)=2 and f(x+y)=2^(x)f(y)+4^(y)f(x) AA x , y in R.`
The number of solutions of `f(x)=2` is04:31View Solution
Exercise (Comprehension) questions and complete solutions for chapter RELATIONS AND FUNCTIONS of CENGAGE of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS RELATIONS AND FUNCTIONS
- Examples
- Exercise (Comprehension)
- Exercise (Matrix)
- Exercise (Multiple)
- Exercise (Numerical)
- Exercise (Single)
- Exercise 1.1
- Exercise 1.10
- Exercise 1.11
- Exercise 1.12
- Exercise 1.13
- Exercise 1.14
- Exercise 1.15
- Exercise 1.2
- Exercise 1.3
- Exercise 1.4
- Exercise 1.5
- Exercise 1.6
- Exercise 1.7
- Exercise 1.8
- Exercise 1.9
- JEE Previous Year
- Solved Examples And Exercises
