Complete Solutions to Illustrations of chapter GETTING STARTED WITH GRAPHS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GETTING STARTED WITH GRAPHS |
| CENGAGE NEW | Illustrations |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Does the following graph represent a function or a relation?
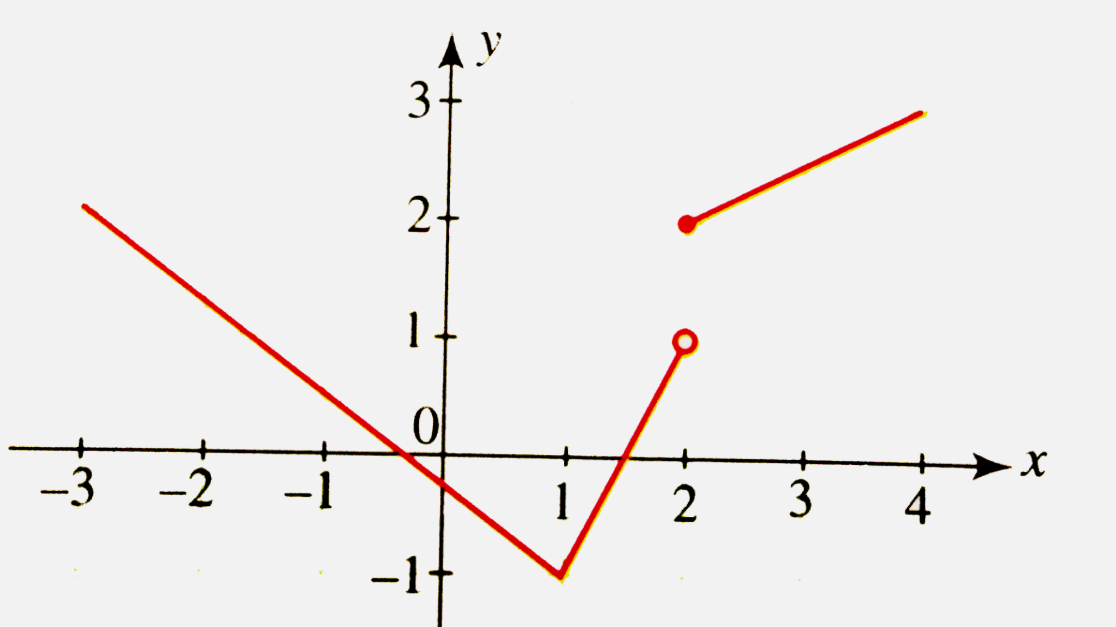 View Solution
View SolutionDoes the graph below represent a function or a relation?
` (##CEN_GRA_C01_S01_002_Q01.png" width="80%">View SolutionDoes the following graph pass the vertical or horizontal line test?
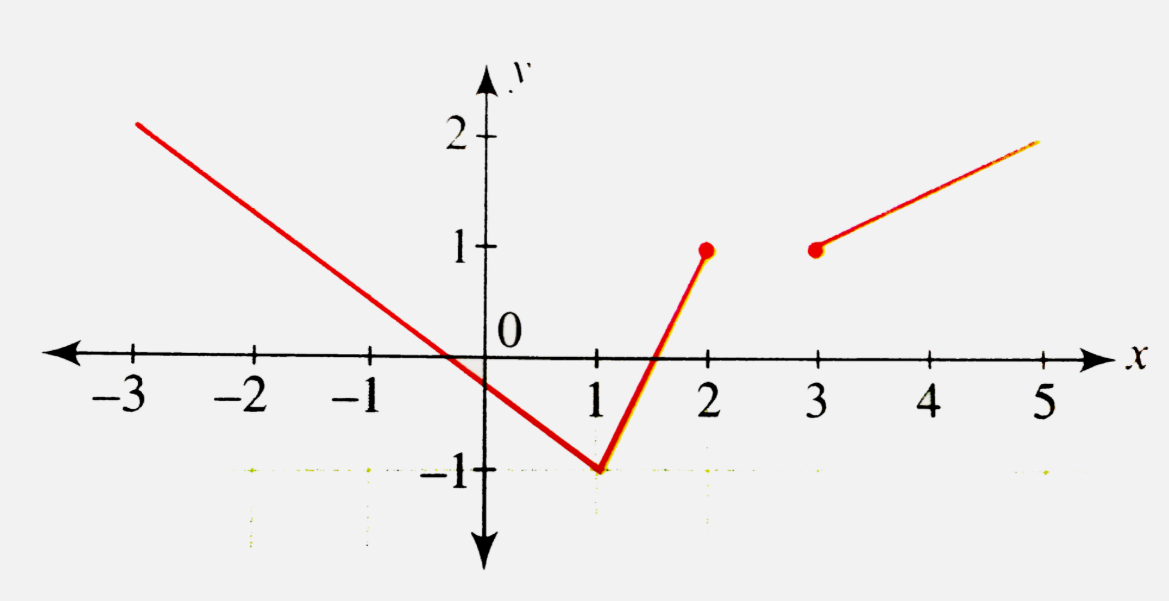 View Solution
View SolutionIn how many points graph of `y=x^3-3x2+5x-3` interest the x-axis?
02:07View SolutionFollowing is the graph of y = f(x).
` (##CEN_GRA_C01_S01_005_Q01.png" width="80%">
Find the roots of the equation ` f(x) = 0, f(x) = 4 and f(x) = 10`.View SolutionWhich of the following pairs of graphs intersect?
(i) ` y = x^(2) -x and y = 1`
(ii) ` y = x^(2) - 2x + 3 and y = sin x `
(iii) ` y = x^(2) - x+1 and y = x-4`View SolutionThe graph of y = f(x) is shown, find the number of solution of f(f(x)) = 2.
` (##CEN_GRA_C01_S01_007_Q01.png" width="80%">View SolutionDoes the fraph of the function ` f (x) = x^(2) -3` have y - axis symmetry?
01:02View SolutionDoes the graph of the function ` f(x) = 1//x^(3) ` have origin symmetry?
01:19View SolutionWhich of the following functions has (have) y-symmetry or origin symmetry?
(i) ` f(x) = x^(2) sin x" "(ii) f(x) = log (x+sqrt(1+x^(2)))`
(iii)` f(x) = (e^(x)+e^(-x))/2" "(iv) f(x) = {{:(0", ""If x is rational "),(1", " "If x is irrational"):}`05:22View SolutionLet ` f : R to R ` be a continuous onto function satisfying `f(x)+f(-x) = 0, forall x in R` . If `f(-3) = 2 and f(5) = 4 ` in [-5, 5], then what is the minimum number of roots of the equation f(x) = 0?
View SolutionLet `f:R->R` and `g:R->R` be two one-one and onto functions such that they are mirror images of each other about the line `y=a`. If `h(x)=f(x)+g(x)`, then `h(x)` is (A) one-one onto (B) one-one into (D) many-one into (C) many-one onto
02:35View SolutionCheck weather the following function/functions is/are periodic or not? Find the period in case the function is periodic.
` (##CEN_GRA_C01_S01_013_Q01.png" width="80%">View SolutionDraw the graph of ` f(x) = {{:(x-2n," "2n le xlt 2n +1),(" where "n in Z." Is "f(x)),(1/2," "2n+1 le x lt 2n+2):}`
periodic? If yes, what is its period?04:55View SolutionThe graph of ` y = f(x) ` is as shown in the following figure.

Find the following values:
(i) `lim_(x to 4) f(x)" "(ii) lim_(x to -3)f(x)`
` (iii) lim_(x to 0^(+))f(x)" "(iv) underset(x to 0^(-)) f(x)`
`(v) lim_(x to 0)f(x)" "(vi) f(-2)`
`(vii) lim_(x to 2^(-))f(x)" "(viii) lim_(x to -2^(-))f(x)`
`(ix) lim_(x to 0)f(x+1)" "(x) f(0)`
` (x i) lim_(x to 0^(+))f(x-2)" "(x ii) lim_(x to 1^(-)) f(x-4)`View SolutionThe graph of ` y = f(x)` is as shown in the following figure.
` (##CEN_GRA_C01_S01_016_Q01.png" width="80%">
Identify the points of discontinuity and give the reason for the same.View SolutionThe graph of f(x) is given. State with reasons the number at which the function is non-differentiable.
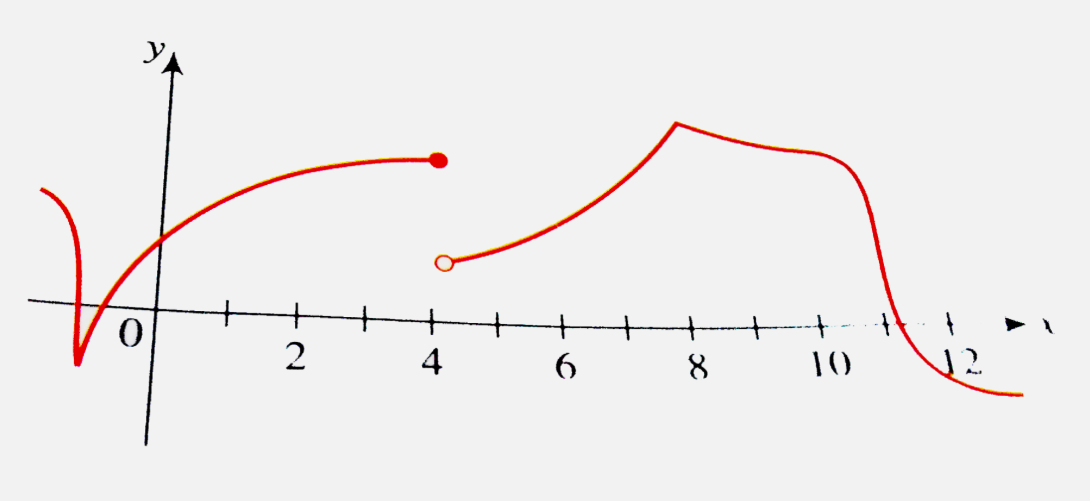 View Solution
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
` (##CEN_GRA_C01_S01_018_Q01.png" width="80%">
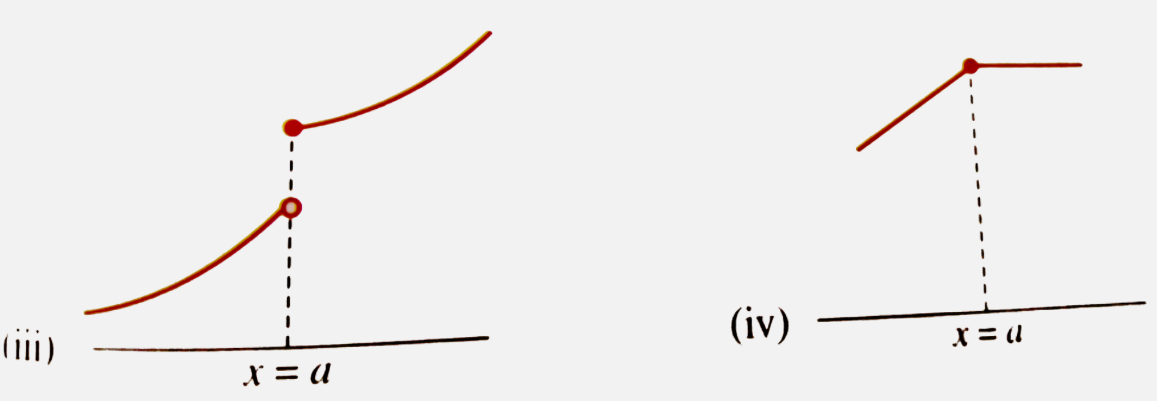 View Solution
View SolutionThe graph of a function is shown in the following figure.
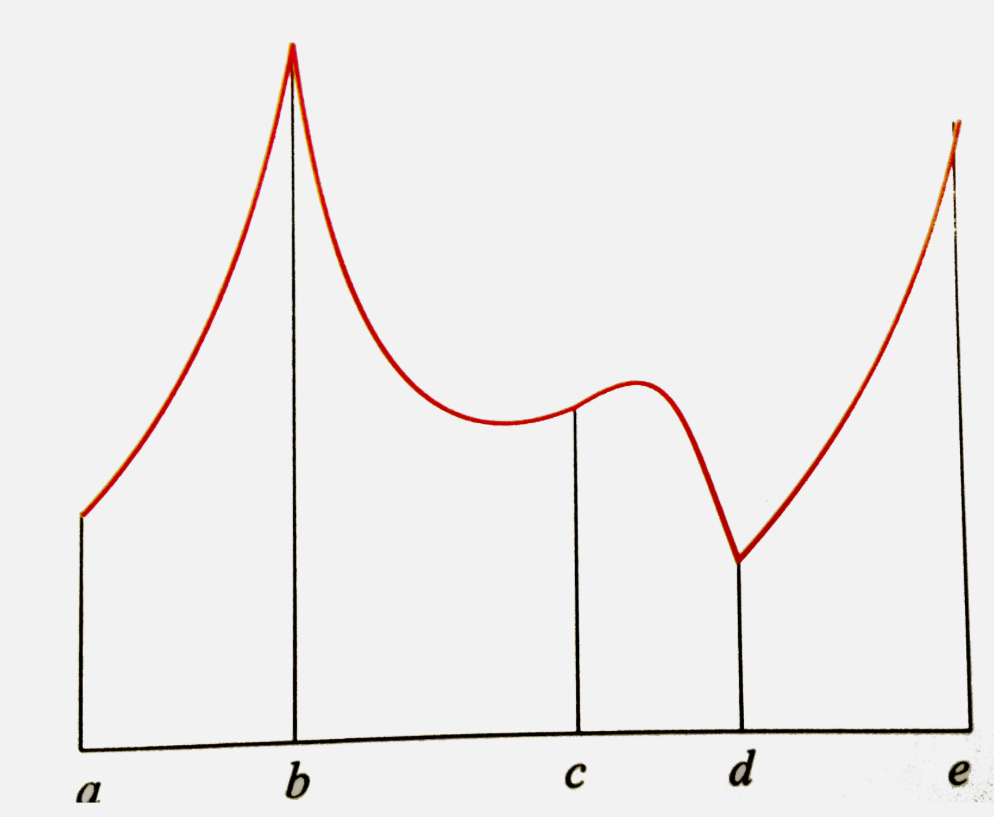
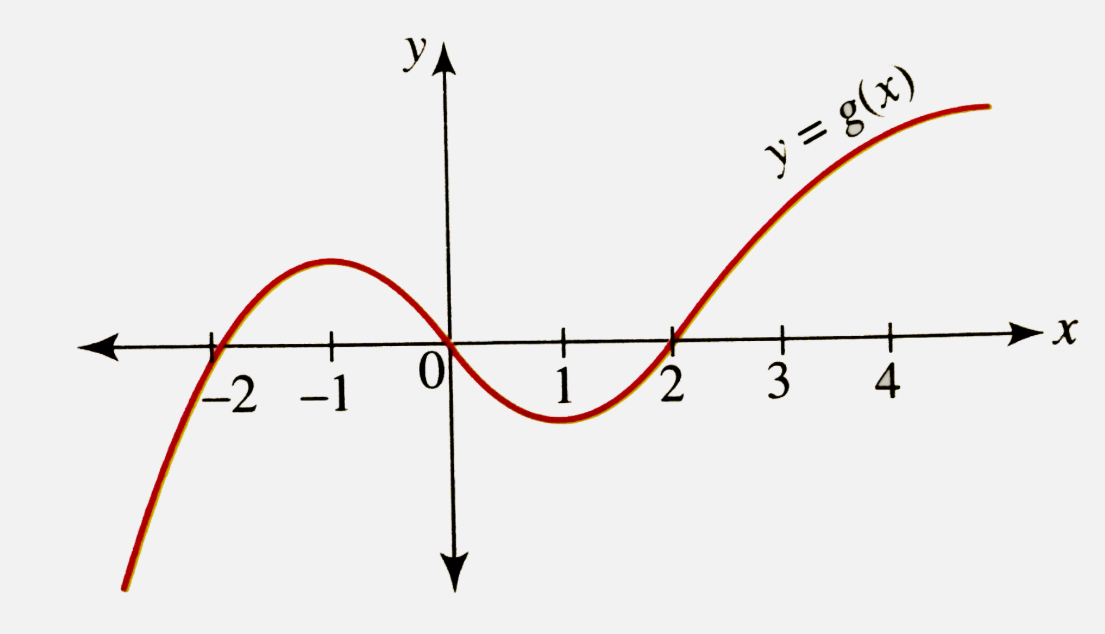
Determine the intervals on which the function is concave up and the intervals on which it is concave down. Find the x - coordinates of any inflection points.View SolutionFor the function g whose graph is given. Arrange the following numbers in increasing order and explain your reasoning.
`g(0), g'(-2), g'(0), g'(2), g'(4)`
 View Solution
View SolutionThe diagram shows the graph of the derivative of a functin f(x) for ` 0 le x le 4 ` with f(0) = 0. Which of the following could be correct statements for y = f(x)?
` (##CEN_GRA_C01_S01_021_Q01.png" width="80%">
(a) Tangent line to y = f(x) at x = 0 makes an angle of ` sec^(-1) sqrt 5` with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.View SolutionIn the following graph, state the absolute and local maximum and minimum values of the function.
` (##CEN_GRA_C01_S01_022_Q01.png" width="80%">View SolutionThe graph of the derivative f'(x) is given in the following figure.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(d) Find the point of inflection.
` (##CEN_GRA_C01_S01_023_Q01.png" width="80%">View SolutionThe graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
` (##CEN_GRA_C01_S01_024_Q01.png" width="80%">View SolutionThe figure shows the graphs of f, f' and f'' . Identify each curve and explain your choices.
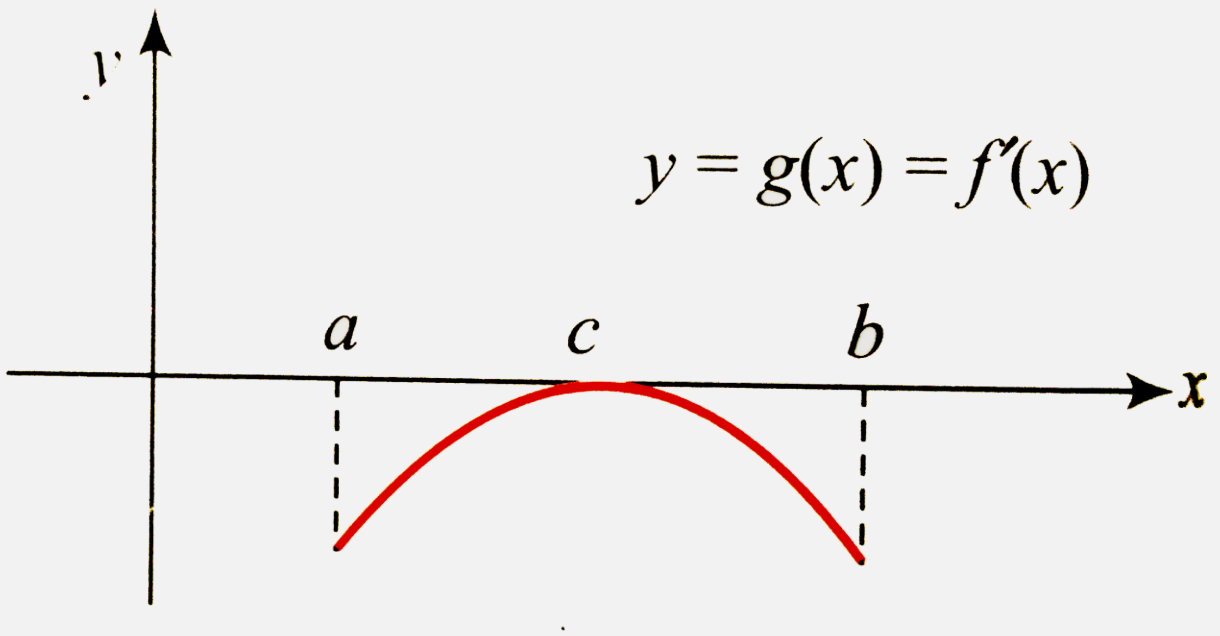
` (##CEN_GRA_C01_S01_025_Q01.png" width="80%">View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, ` a le x le b`.
(c) How many points of inflection the graph of ` y = f(x), a le x le b`, has?
(d) Find the points of local maxima/minima of` y = f(x), a lt x b`.
(e) How many roots equation ` f''(x) = 0` has?
 View Solution
View SolutionFind the asymptote of the function ` y = (2x^(2) + 3x + 1)/ x` if any.
02:27View SolutionFind the horizontal, vertical and oblique asymptotes of each of the curves.
`{:((a),y=x/(x+4),,(b),y=(x^(2)+4)/(x^(2)-1)),((c),y=x^(3)/(x^(2)+3x-10),,(d),y=(x^(3)+1)/(x^(3)+x)),((e),y=x/(root(4)(x^(4)+1)),,(f),y=(x-9)/(sqrt(4x^(2)+3x+2))),((g),y=1/(2^(x)-1),,(h),y=1/(log_(e) x)),((i),y= 1/(2^(x) - 1),,,):}`View Solution
Illustrations questions and complete solutions for chapter GETTING STARTED WITH GRAPHS of CENGAGE MATHS (HINGLISH) of Class 12
