The graph of f(x) is given. State with reasons the number at which the function is non-differentiable.
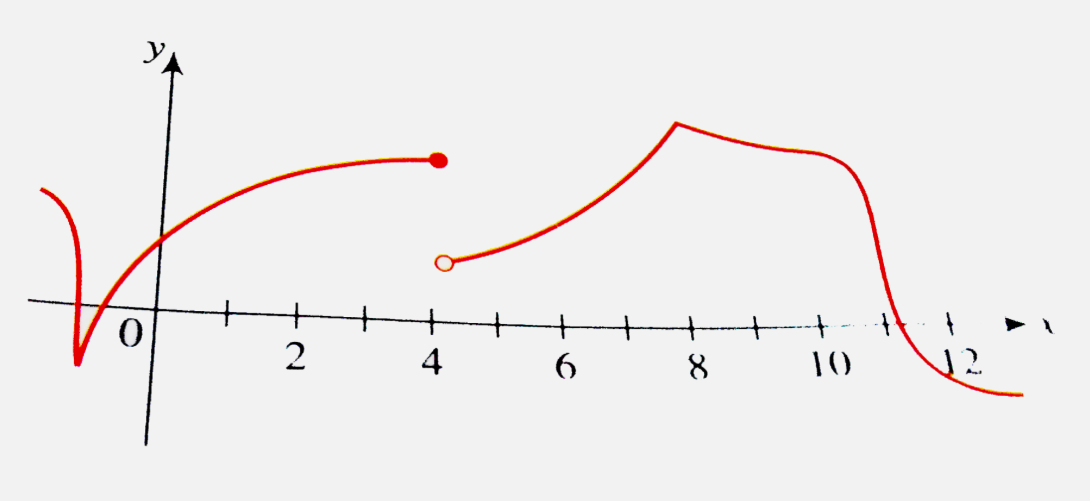
f (x) is non- differentiable at x =- 1 as the function has vertical tangent at this point.
f(x) is non-differentiable at x = 4 as the function is discontinuous at this point.
f(x) is non-differentiable at x = 8 as the function has kink at this point, where L.H.D. and R.H.D. are different.
f(x) is non-differentiable at x = 11 as the function has vertical tangent at this point.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- FUNCTIONSBOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank
30 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
Similar Questions
The graph of f is shown. State, with reason, the numbers at which f is not differentiable.
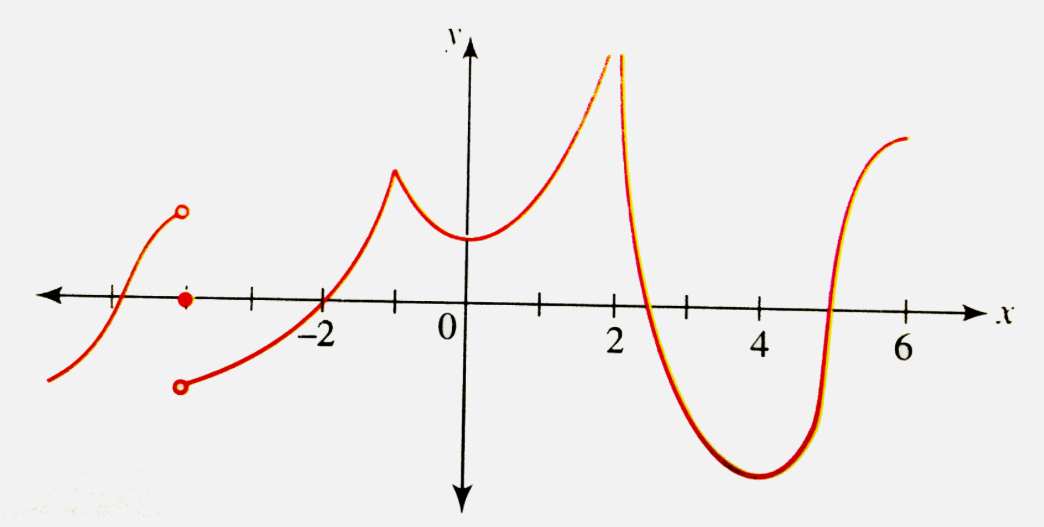
View SolutionThe graph of f is shown. State, with reason, the numbers at which f is not differentiable.

View SolutionWhich of the function is non-differential at x=0? f(x)=x|x|
View SolutionWhich of the function is non-differential at x=0? f(x)=∣∣x3∣∣
View SolutionWhich of the function is non-differential at x=0? f(x)=cos|x|
View SolutionWhich of the function is non-differential at x=0? f(x)=∣∣x3∣∣
View SolutionWhich of the function is non-differential at x=0? f(x)=x|x|
View SolutionWhich of the function is non-differential at x=0? f(x)=cos|x|
View Solutionf:(0,∞)⇒R f(x)=max(x2,|x|) then the number of points where function is non- differentiable,is
View SolutionIf f(x)=x+{−x}+[x], where [x] and {x} denotes greatest integer function and fractional part function respectively, then find the number of points at which f(x) is both discontinuous and non-differentiable in [−2,2].
View Solution
