Complete Solutions to Exercise 1.1 of chapter MAGNETIC FIELD AND MAGNETIC FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD AND MAGNETIC FORCES |
| CENGAGE PHYSICS | Exercise 1.1 |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
A charged particle of mass 5 mg and charge `q= +2 mu C` has velocity `vec v = 2 hat i - 3 hat j + 4 hat k.` Find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field `vec B = 3 hat j - 2 hat k. vec v and vec B` are in `ms^-1 and Wbm^-2` , respectively.
View SolutionA charged particle has acceleration `vec a = 2 hat i + x hat j ` in a megnetic field `vec B = - 3 hat i + 2 hat j - 4 hat k.` Find the value of x.
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionRepeat above Question 3, if the charge is negative and the angle made by the boundary with the velocity is `theta = pi/6.`
View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if
(a) `dgt (m u)/(qB)`
(b) `dlt (m u)/(qB)`
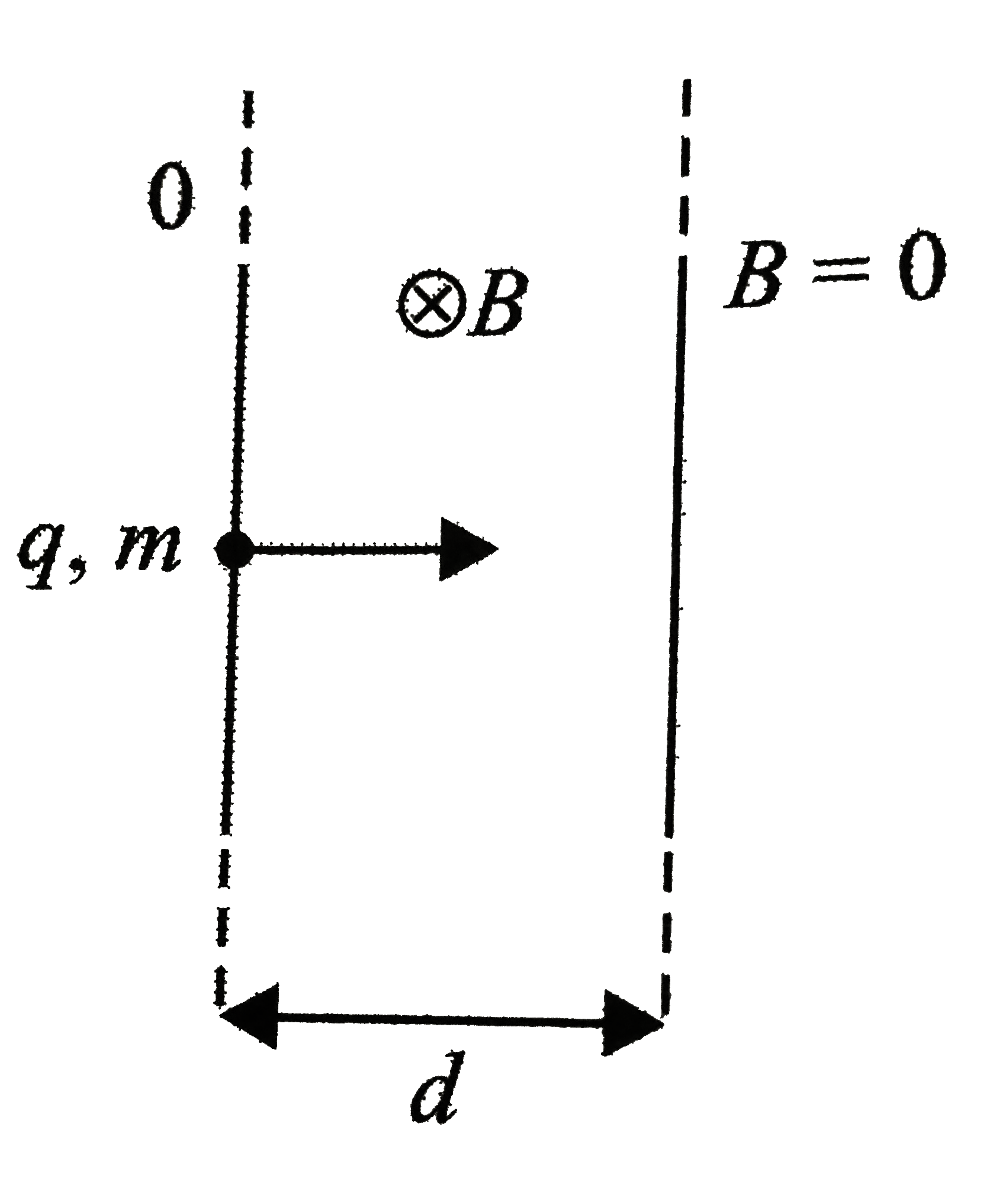
View SolutionIn Fig. what should be the speed of the charged particle so that it cannot collide with the upper wall? Also, find the coordinates of the point where the particle strikes the lower plate in the limiting case of velocity.
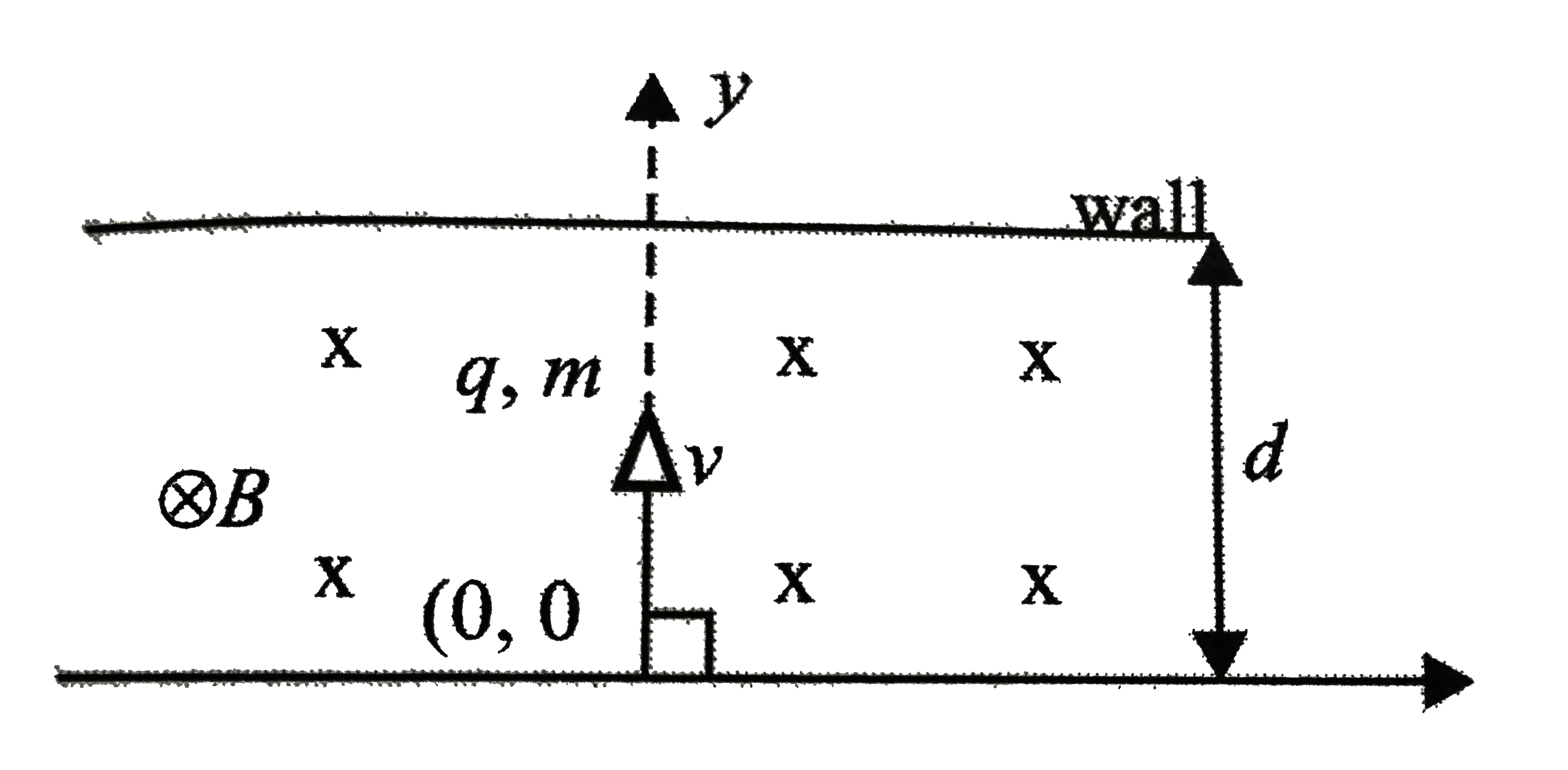
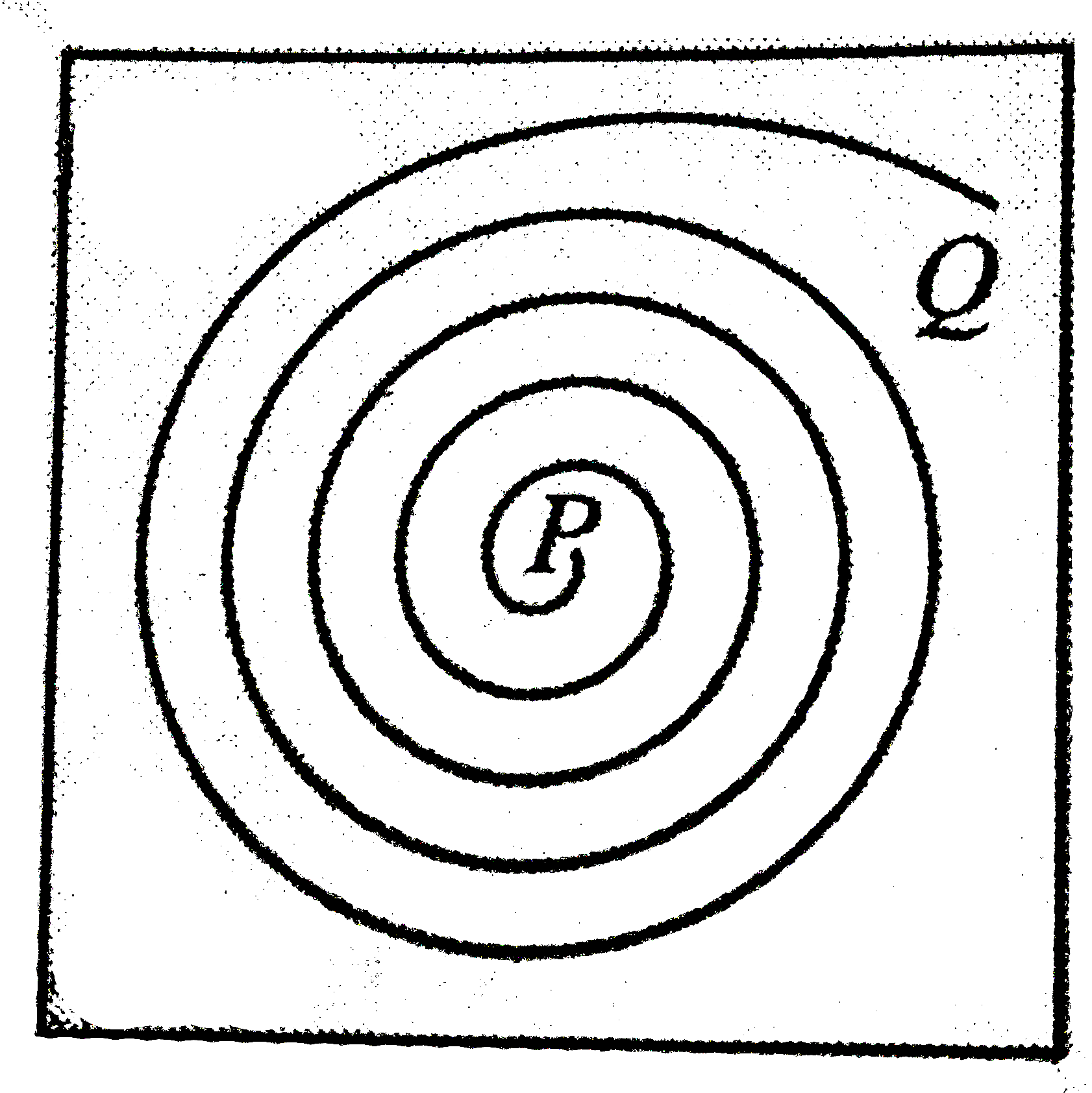
View SolutionA charged particle enters a region which offers a resistance against its motion and a uniform mangetic field exists in the region. The particle traces a spiral path as shown in Fig. 1.29. State the following statements as True or False.
(a) Component of magnetic field in the plane of spiral is zero.
(b) Particle enters the region at Q.
(c) If magnetic field is outwards, then the particle is positively charged.
(d) All of these.

View SolutionAn electron moves in a uniform magnetic field and follows a spiral path as shown in Fig. 1.30. State the following statements as True or False.
a. Angular velocity of the electron remains constant.
b. Magnitude of velocity of the electron decreases continuously.
c. Net force on the particle is always perpendicular to its direction of motion.
d. Magnitude of net force on the electron decreases continuously.
View SolutionA charged particle moves in a gravity free space where an electric field of strength E and a magnetic field of induction B exist. State the following statements as True of False.
a. If `E pi 0 and B pi 0,` velocity of the particle may remain constant.
b. If `E = 0`, the particle cannot trace a circular path.
c. If `E=0`, kinetic energy of the particle remains constant.
View SolutionA particle with charge `-5.60 nC` is moving in a uniform magnetic field `vec B = -(1.25T) hat k.` The magnetic force on the particle is measured to be `vec F = -(3.36 xx 10^-7 N) hat i + (7.42 xx 10^-7 N) hat j.`
a. Calculate all components of the velocity of the particle from this information.
b. Are there components of the velocity that cannot be determined by the measurement of the force? Explain.
c. Calculate the scalar product `vec v . vec F.` What is the angle between v and F?
View SolutionA particle with charge `7.00 mu C` is moving with velocity `vec v =- (4xx10^3 ms^-1) hat j.` The magnetic force on the particle is measured to be `vec F = +(8.4 xx 10^-2 N) hat i - (5.60 xx 10^-2 N) hat k.`
a. Calculate all the components of the magnetic field you can from this information.
b. Are there components of the magnetic field that cannot be determined by measurement of the force? Explain.
c. Calculate the scalar product `vec B. vec F.` What is the angle between `vec B and vec F`?
View SolutionA particle with charge `6.40 xx 10^(-19) C ` travels in a circular orbit with radius 4.68 mm due to the force exerted on it by a magnetic field of magnitude 1.65 T and perpendicular to the orbit.
a. What is the magnitude of the linear momentum `vec P` of the particle?
b. What is the magnitude of the angular momentum `vec L` of the particle?
View SolutionFigure 1.31 shows the trace of the path of a charged particle in a bubble chamber. Assume that the magnetic field is into the plane of the paper with magnitude 0.4 T. The smooth spiral path occurs because the particle loses energy in ionizing molecules along the path.
a. Which part of the path corresponds to higher kinetic energy for the particle? Inner or outer part of spiral.
b. Is the charge positive or negative?
c. The radius of curvature ranges from 70 mm to 10 mm. What is the range of values of the magnitude of momentum if the magnitude of the charge is e?

View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA beam of equally charged particles after being accelerated through a voltage V enters into a magnetic field B as shown in Fig. 1.31. It is found that all the particles hit the plate between C and D. Find the ratio between the masses of the heaviest and lightest particles of the beam.

View SolutionA proton and an alpha particle are projected in a magnetic field which exists in the width of region d. Compare the angles of deviation suffered by the proton and the alpha particle if before entering the magnetic field both the particles.
a. have the same momentum,
b. have the same kinetic energy, and
c. are accelerated through the same potential difference. Take `m_alpha = 4 m_p, q_alpha = 2 q_p.`
View SolutionA beam of singly ionized atoms of carbon (each charge +e) all have the same speed enters a mass spectrometer, as shown in Fig. The ions strike the photographic plate in two different locations 5 cm apart. The `._12C_6` isotope traces a path of smaller radius, `15.0 cm`. What is the atomic mass number of other isotope ?
 .
.
View SolutionWhen a proton has a velocity
`v=(2hati+3hat)xx10^(6)ms^(-1)`, ti experiences a force `F=-(1.28xx10^(-13)hatk)N.` When its velocity is along the Z-axis then it experiences a force along the X-axis.What is the magnetic field ?
View SolutionThe force on a charged particle moving in a magnetic field can be computed as the vector sum of the force due to each separate component of the magnetic field. As an example, a particle with charge q is moving with speed v in the -y direction. It is moving in a uniform magnetic field `vec B = B_x hat i + B_y hat j + B_z hat k.`
a. What are the components of the force `vec F` exerted on the particle by the magnetic field?
b. If `qgt0`, what must the signs of the components of `vec B` be if the components of `vec F` are all non-negative?
c. If `qlt0 and B_x = B_y = B_z gt 0,` find the direction and magnitude of `vec F` in terms of `|q|,` v and `B_x.`
View SolutionA particle of charge `qgt0` is moving at speed v in the +z direction through a region of uniform magnetic field. The magnetic force on the particle `vec F = F_0 (3 hat i + 4 hat j)`, where `F_0` is a positive constant.
(a) Determine the components `B_x, B_y` and `B_z` or at least as many of the three components as is possible from the information given.
(b) If it is given in addition that the magnetic field has magnitude `6F_0 / (qv)` , determine the magnitude of `B_z`.
View SolutionProtons having a kinetic energy of 50 eV are moving in the positive x-direction and enter a magnetic field `B=0.5m hat k T` directed out of the plane of the page and extending from `x=0 to x=1 m` as shown in Fig. 1.34.
a. Calculate the y-component of the protons' momentum as they leave the magnetic field.
b. Find the angle `phi` between the initial velocity vector of the proton beam and the velocity vector after the beam emerges from the field. Ignore relativistic effects and note that `1 eV=1.60 xx 10^(-19) J.`

View SolutionElectrons in a beam are accelerated from rest through a potential difference `Delta V`. The beam enters an experimental chamber through a small hole. As shown in Fig. 1.35, the electron velocity vector lie within a narrow cone of half angle `phi` oriented along the beam axis. We wish to use a uniform magnetic field directed parallel to the axis to focus the beam, so that all of the electrons can pass through a small exit port on the opposite side of the chamber after they travel the length d of the chamber. What is the required magnitude of the magnitude field?

View Solution
Exercise 1.1 questions and complete solutions for chapter MAGNETIC FIELD AND MAGNETIC FORCES of CENGAGE PHYSICS (ENGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS MAGNETIC FIELD AND MAGNETIC FORCES
- Archives Assertion-reasion
- Archives Comprehension
- Archives Fill In The Blank
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives True /false
- Comphension Based
- Comprehension type
- Exercise 1.1
- Exercise 1.2
- Exercise1.3
- Exercises Assertion -reasoning
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises Subjective
- Illustration
- Multiple
- Multiple Correct Answer type
- Single Correct Answer Type
- Solved Example
- Subjective
- Subjective type