Complete Solutions to Exercises Linked Comprehension of chapter MAGNETIC FIELD AND MAGNETIC FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD AND MAGNETIC FORCES |
| CENGAGE PHYSICS | Exercises Linked Comprehension |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
The circuit in fig. consists of wires at the top and bottom and identical metal springs at the left and right sides.The wire at the bottom has a mass of 10.0g and is 5.00cm long. The wire is hanging as shown in the figure. The springes stretch 0.500 cm under the weight of the wire, and the circuit has a total resistance of `12.0Omega`. When a magnetic field is turned on the springes stretch an additional 0.300 cm.
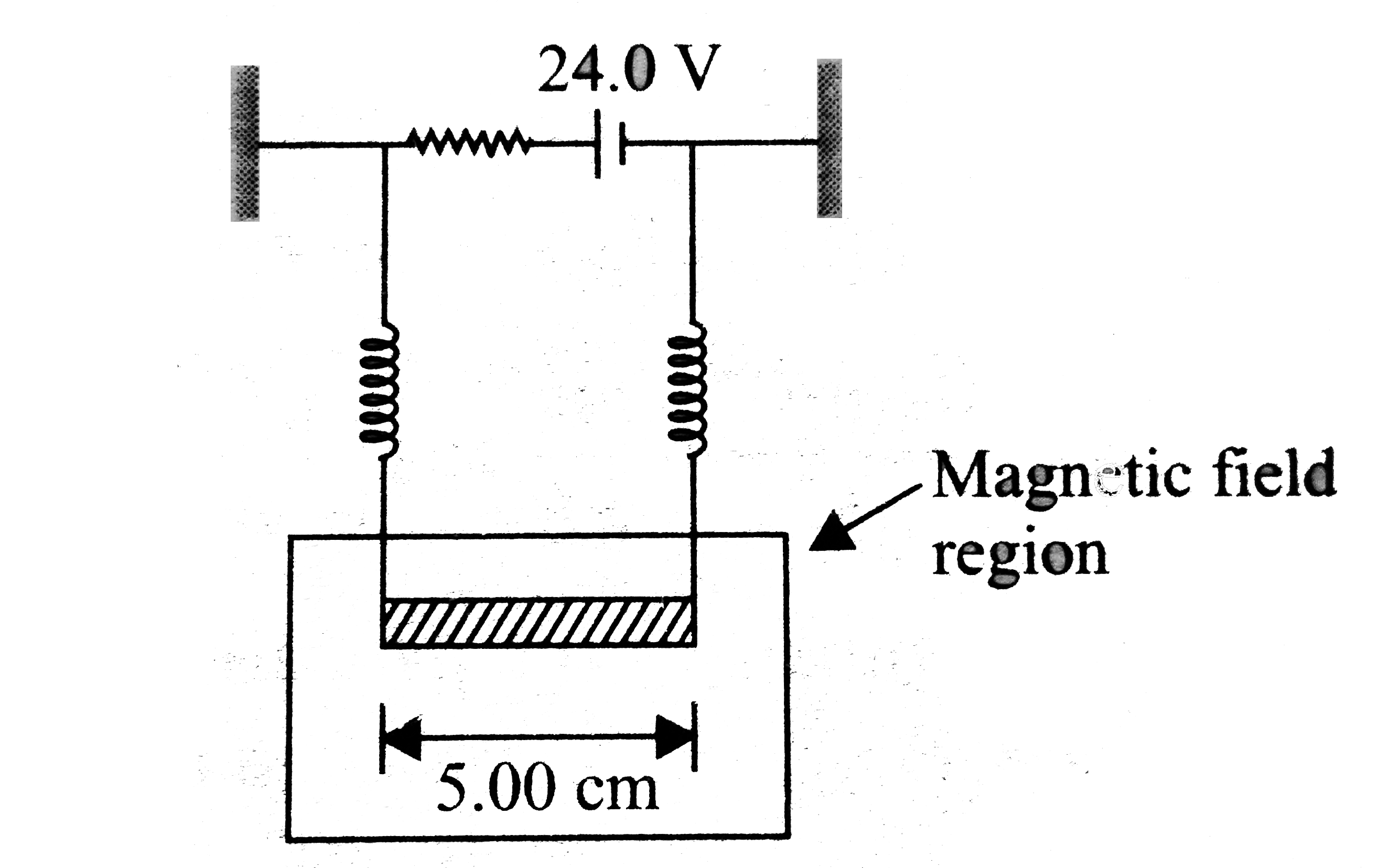
From the above statements we can conclude that
View SolutionThe circuit in fig. consists of wires at the top and bottom and identical metal springs at the left and right sides.The wire at the bottom has a mass of 10.0g and is 5.00cm long. The wire is hanging as shown in the figure. The springes stretch 0.500 cm under the weight of the wire, and the circuit has a total resistance of `12.0Omega`. When a magnetic field is turned on the springes stretch an additional 0.300 cm.
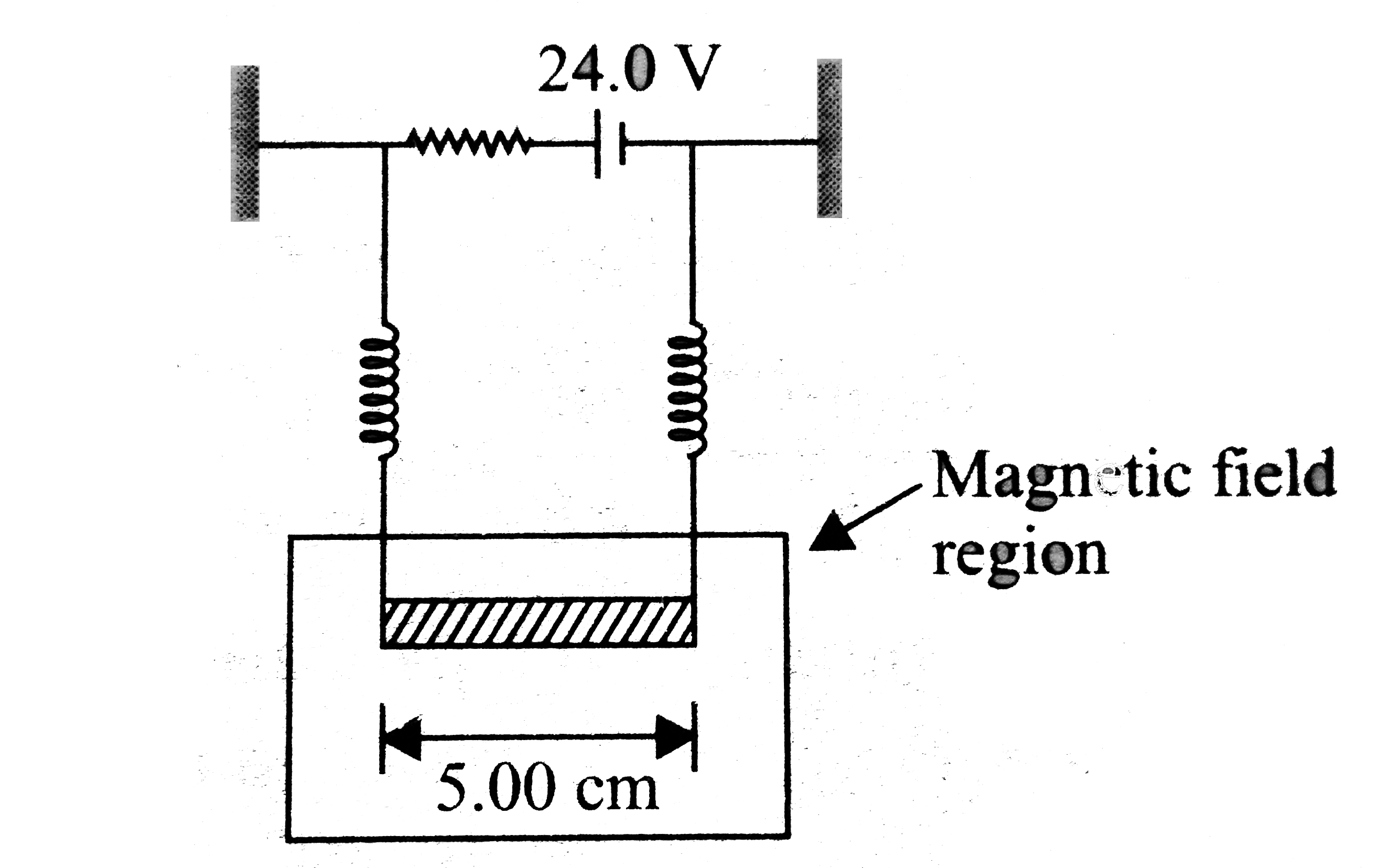
The magnitude of magnetic field is
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle `theta` with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle `theta` with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle `theta` with the field. At the same moment , another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field of induction is B.
What would be the speed of second particle so that both particles meet again and again after a regular interval of time, which should be minimum?
View SolutionA charged particle carrying charge `q=10 muC` moves with velocity `v_1=10^6 ,s^-1` at angle `45^@` with x-axis in the xy plane and experience a force `F_1=5sqrt2 mN` along the negative z-axis. When the same particle moves with velocity `v_2=10^6 ms^-1` along the z-axis, it experiences a force `F_2` in y-direction.
Find the magnetic field `vecB`.
View SolutionA charged particle carrying charge `q=10 muC` moves with velocity `v_1=10^6 ms^-1` at angle `45^@` with x-axis in the xy plane and experience a force `F_1=5sqrt2 mN` along the negative z-axis. When the same particle moves with velocity `v_2=10^6 ms^-1` along the z-axis, it experiences a force `F_2` in y-direction.
Find the magnitude of the force `F_2`.
View SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

In static condition, find the current through rod PC.
View SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

Net torque applied by the tension in strings can be related as
View SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

The value of V can be related with m, B and r as
View SolutionIn a region, magnetic field along x-axis changes according to the graph given in fig.

If time period, pitch and radius of helix path are `T_0, P_0 and R_0`, respectively, and if the particle is projected at an angle `theta_0` with the positive x-axis towards positive y-axis in x-y plane, then
select the correct statement
View SolutionIn a region, magnetic field along x-axis changes according to the graph given in fig.

If time period, pitch and radius of helix path are `T_0, P_0 and R_0`, respectively, and if the particle is projected at an angle `theta_0` with the positive x-axis towards positive y-axis in x-y plane, then
select the correct statement:
View SolutionThe region between x=0 and x=L is filled with uniform constant magnetic field 25(T)`hatk`. A particle of mass m=50g having positive charge q=1C and velocity `vecV_0=50sqrt3hati+50hatjms^-1` enters the region of the magnetic field. Neglect gravity throughout the question.
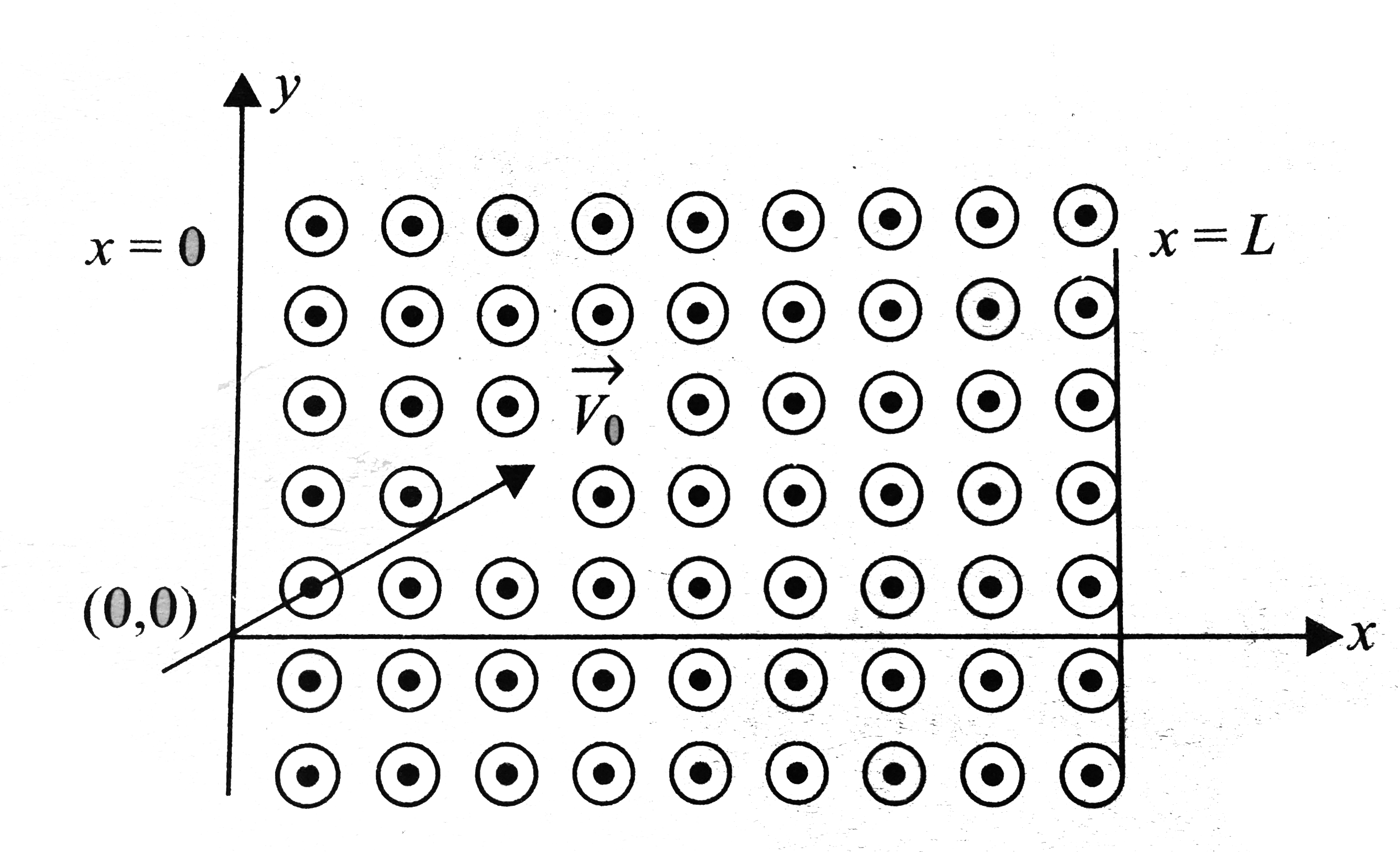
The value of L if the particle emerges from the region of magnetic field with its velocity `100(ms^-1)hati` is
View SolutionThe region between x=0 and x=L is filled with uniform constant magnetic field 25(T)`hatk`. A particle of mass m=50g having positive charge q=1C and velocity `vecV_0=50sqrt3hati+50hatjms^-1` enters the region of the magnetic field. Neglect gravity throughout the question.

The maximum and minimum values of L such that velocity of emerging particle makes angle `pi//3` with the y-axis are
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of `60^@` with the positive x-axis in x-y plane. When the x-coordinate of particle becomes `sqrt3mv^2//qE` a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of `60^@` with the positive x-axis in x-y plane. When the x-coordinate of particle becomes `sqrt3mv^2//qE` a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of `60^@` with the positive x-axis in x-y plane. When the x-coordinate of particle becomes `sqrt3mv^2//qE` a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge `q//m` leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity `v_0`

The coordinate `y_n` of the particle when it crosses the y-axis for the `n^(th)` time is
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge `q//m` leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity `v_0`

The angle `alpha` between the particle's velocity vector and y-axis at and moment is
View SolutionA thin, 50 cm long metal bar with mass 750 g rests on, but is not attrached to, two metallic supports in a uniform 0.450T magnetic field, as shown in fig. A battery and a `25Omega` resistor in series are connected to the supports.

What is the largest voltage the battery can have without breaking the circuit at the supports?
View SolutionA thin, 50 cm long metal bar with mass 750 g rests on, but is not attrached to, two metallic supports in a uniform 0.450T magnetic field, as shown in fig. A battery and a `25Omega` resistor in series are connected to the supports.

The battery voltage has the maximum value calculated in above question. If the resistor suddenly gets partially short-circuited, decreasing its resistance to `2 Omega`, find the initial accleration of the bat.
View SolutionA conductor bar with mass m and length L slides over horizontal rails that are connected to a voltage source. The voltage source maintains a constant current I in the rails and bar, and constant, uniform, vertical magnetic field `vecB` fills the region between the rails (as shown in Fig.)

Find the magnitude and direction of the net force on the conducting bar. Ignore friction, air resistance and electrical resistance.
View SolutionA conductor bar with mass m and length L slides over horizontal rails that are connected to a voltage source. The voltage source maintains a constant current I in the rails and bar, and constant, uniform, vertical magnetic field `vecB` fills the region between the rails (as shown in Fig.)
If the bar has mass m, find the distance d that the bar must move along the rails from rest to attain speed v.

View SolutionA thin, uniform rod with negligible mass and length 0.200m is attached to the floor by a frictionless hinge at point P (as shown in fig) A horizontal spring with force constant `k=4.80Nm^-1` connects the other end of the rod to a vertical wall. The rod to a vertical wall. The rod is in a uniform magnetic field B=0.340T directed into the plane of the figure. There is current I=6.50 A in the rod, in the direction shown.
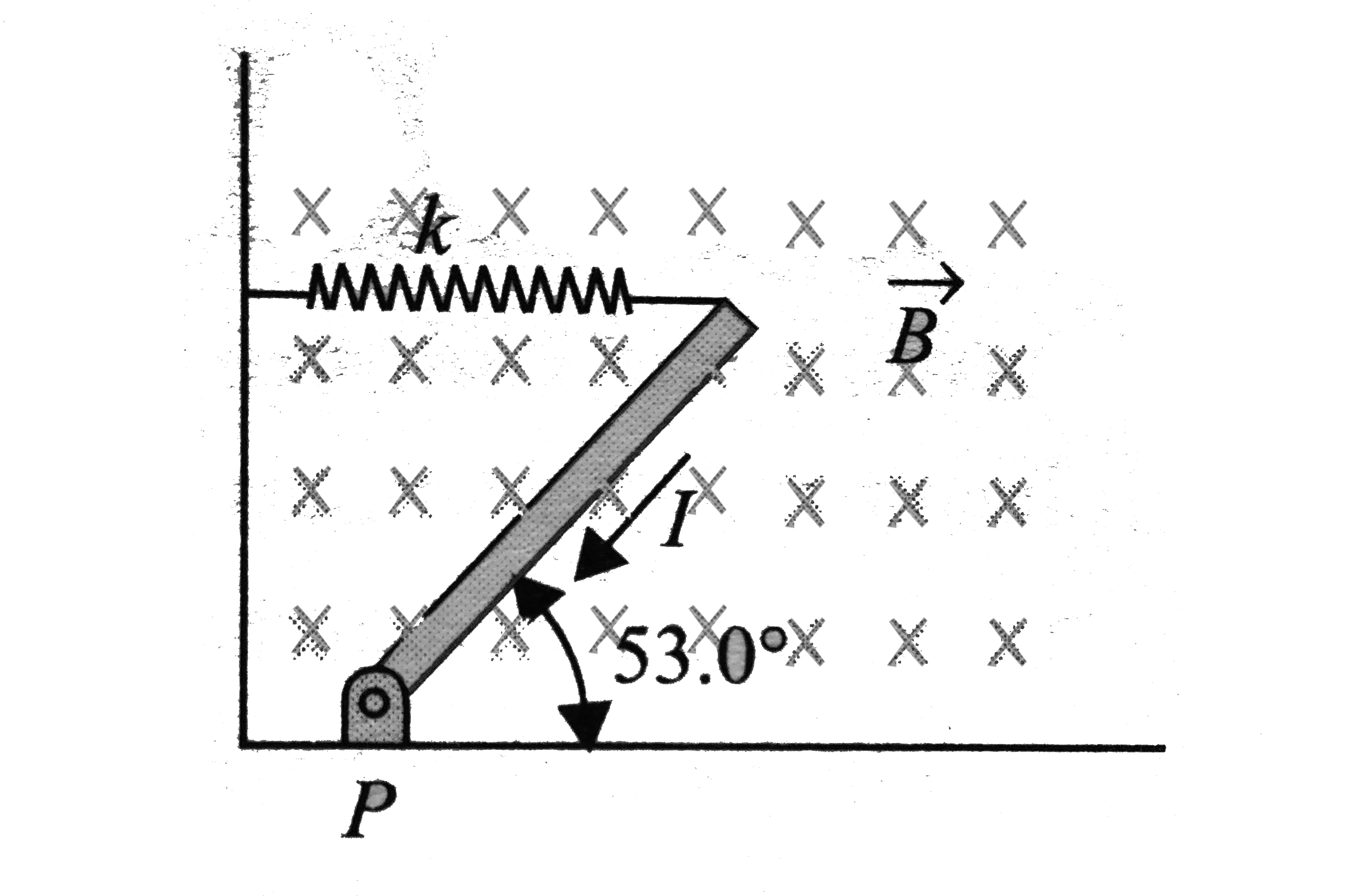
Calculate the torque due to the magnetic force on the rod, for an axis at P.
View SolutionA thin, uniform rod with negligible mass and length 0.200m is attached to the floor by a frictionless hinge at point P (as shown in fig) A horizontal spring with force constant `k=4.80Nm^-1` connects the other end of the rod to a vertical wall. The rod to a vertical wall. The rod is in a uniform magnetic field B=0.340T directed into the plane of the figure. There is current I=6.50 A in the rod, in the direction shown.
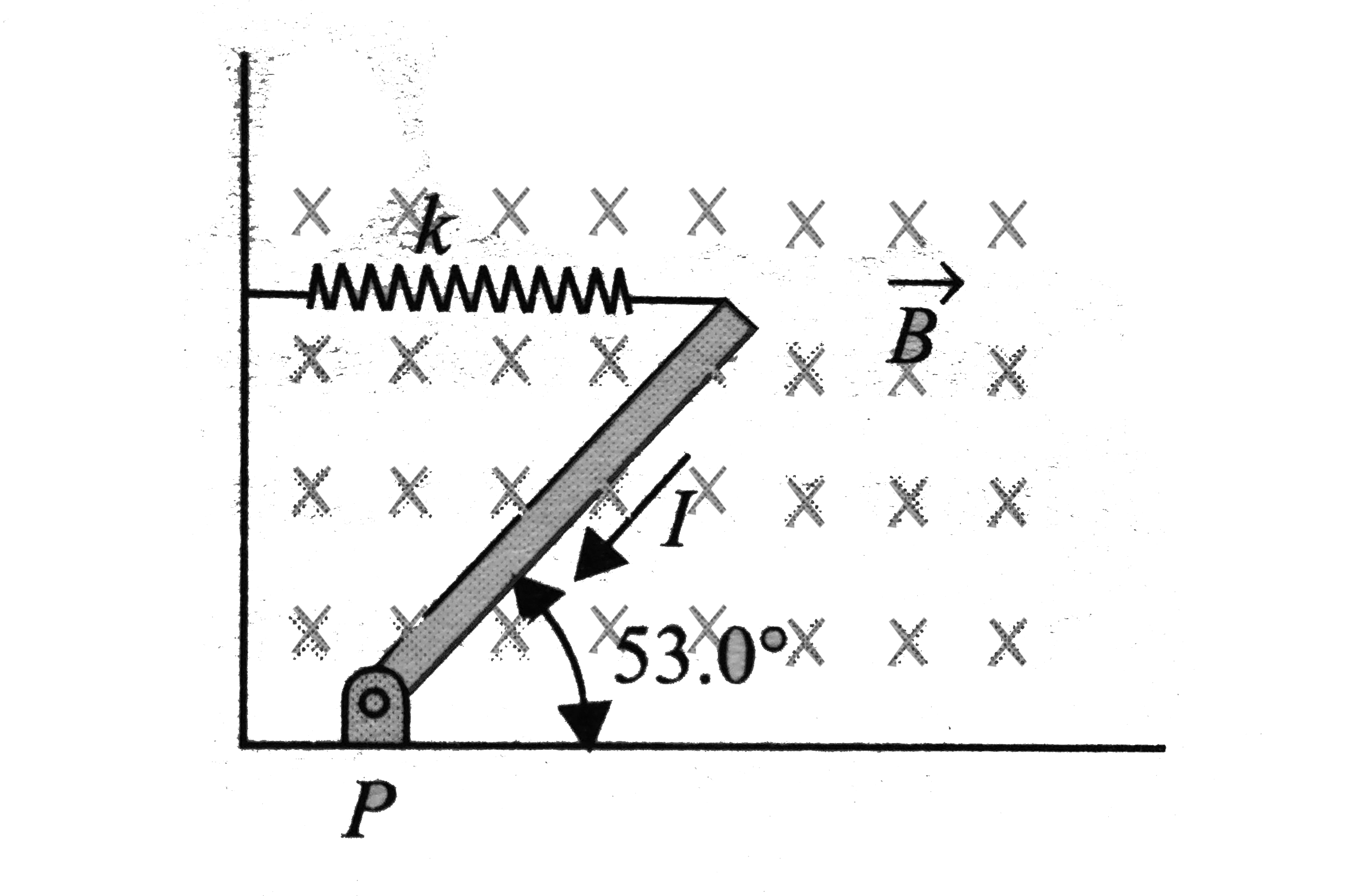
When the rod is in equilibrium and makes an angle of `53.0^@` with the floor, is the spring stretched or compressed?
View SolutionA wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field `vecB=(2hati-3hatj_)T` is present in the region.

Find the net force on the loop shown.
View SolutionA wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field `vecB=(2hati-3hatj-hatk)T` is present in the region.

Find the magnetic moment vector of the loop.
View SolutionA wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field `vecB=(2hati-3hatj+hatk)T` is present in the region.

Find the net torque on the loop.
View Solution
Exercises Linked Comprehension questions and complete solutions for chapter MAGNETIC FIELD AND MAGNETIC FORCES of CENGAGE PHYSICS (ENGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS MAGNETIC FIELD AND MAGNETIC FORCES
- Archives Assertion-reasion
- Archives Comprehension
- Archives Fill In The Blank
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives True /false
- Comphension Based
- Comprehension type
- Exercise 1.1
- Exercise 1.2
- Exercise1.3
- Exercises Assertion -reasoning
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises Subjective
- Illustration
- Multiple
- Multiple Correct Answer type
- Single Correct Answer Type
- Solved Example
- Subjective
- Subjective type