Complete Solutions to Exercises Single Correct of chapter MAGNETIC FIELD AND MAGNETIC FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD AND MAGNETIC FORCES |
| CENGAGE PHYSICS | Exercises Single Correct |
| Number Of Questions | 70 |
| Academic Year | 2023-24 |
A neutron, a proton, an electron and an `alpha-`particle enter a region of uniform magnetic field with equal velocities. The magnetic field is perpendicular to the paper and directed into it. The tracks of particles are labeled in Fig. 1.132. The neutron follows the track

View SolutionA U tube of uniform square cross-sectional side a has mercury in it. Current I is passed between sealed electrodes x and y. A magnetic field `B` is applied across horizontal section perpendicular to the plane of diagram. The difference in mercury levels is [Given: `rho` = density of mercury]
 .
.
View SolutionWhen an electron is accelerated through a potential difference `V`, it experience a force `F` through as uniform transverse magnetic field. If the potential difference is increased to `2 V,` the force experoenced by the electron in the same magnetic field is
View SolutionAn electron is moving along positive x-axis. To get it moving on an anticlockwise circular path in x-y plane, a magnetic field is applied
View SolutionTwo particles X and Y having equal charges, after being accelerated through the same potential difference, enter a region of uniform magnetic field and describe circular paths of radii `R_1 and R_2,` respectively. The ratio of masses of X and Y is
View SolutionAn electron of mass `0.90 xx 10^(-30)` kg under the action of a magnetic field moves in a circle of 2.0 cm radius at a speed `3.0 xx 10^6 ms^-1`. If a proton of mass `1.8 xx 10^(-27) kg` was to move in a circle of the same radius in the same magnetic field, then its speed will be
View SolutionA charged particle of mass `10^-3 kg` and charge `10^-5 C` enters a magnetic field of induction 1 T. If `g = 10 ms^-2,` for what value of velocity will it pass straight through the field without deflection?
View SolutionA particle of mass `2 xx 10^-5 kg` moves horizontally between two horizontal plates of a charged parallel plate capacitor between which there is an electric field of `200 NC^-1` acting upward. A magnetic induction of 2.0 T is applied at right angles to the electric field in a direction normal to both `vec B and vec v.` If g is `9.8 ms^-2` and the charge on the particle is `10^-6 C,` then find the velocity of charge particle so that it continues to move horizontally
View SolutionA charged particle moves along a circle under the action of possible constant electric and magnetic fields. Which of the following are possible?
View SolutionTwo particles Y and Z emitted by a radioactive source at P made tracks in a chamber as illustrated in the Fig. 1.134. A magnetic field acts downward into the paper. Careful measurements showed that both tracks were circular, the radius of Y track being half that of the Z track. Which one of the following statements is certainly true?

View SolutionA proton and an `alpha-`particle enter a uniform magnetic field moving with the same speed. If the proton takes `25 mu s` to make 5 revolutions, then the periodic time for the `alpha-` particle would be
View SolutionAn electron is launched with velocity `vec v` in a uniform magnetic field `vec B.` The angle `theta` between `vec v and vec B` lies between 0 and `pi /2`. Its velocity vector `vec v` returns to its initial value in a time interval of
View SolutionA charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one pint. If a magnetic field is switched on in the vertical direction, the tension in the string
View SolutionA charged particle moves with velocity `vec v = a hat i + d hat j` in a magnetic field `vec B = A hat i + D hat j.` The force acting on the particle has magnitude F. Then,
View SolutionA particle with a specific charge s is fired with a speed v toward a wall at a distance d, perpendicular to the wall. What minimum magnetic field must exist in this region for the particle not to hit the wall?
View SolutionA charged particle begins to move from the origin in a region which has a uniform magnetic field in the x-direction and a uniform electric field in the y-direction. Its speed is v when it reaches the point (x, y, z). Then, v will depend
View SolutionTwo metal strips of length l each are placed parallel to each other in contact with an electric circuit as shown in Fig. 1.135. The entire structure is placed on a smooth horizontal floor in a region in which magnetic field is existing in vertical direction. The distance travelled by the wire as a function of time is best given by
where `t_0 = sqrt ((2lmR)/(EBb))`

View SolutionA particle of charge q and mass m is projected with a velocity `v_(0)` towards circular region having uniform magnetic field B perpendicular and into the plane of paper, from point Pas shown in figure. R is the radius and O is the centre of the circular region. If the line OP makes an angle `theta` with the direction of `v_(0)` then the value of `v_(0)` so that particle passes through O is

View SolutionAn electron moving with a speed u along the positive x-axis at `y=0` enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then

View SolutionAn electron is accelerated from rest through a potential difference V. This electron experiences a force F in a uniform magnetic field. On increasing the potential difference to V', the force experienced by the electron in the same magnetic field becomes 2F. Then, the ratio `(V'//V)` is equal to
View SolutionA particle of charge q and mass m starts moving from the origin under the action of an electric field `vec(E) = E_(0)hat(i)` and a magnetic field `vec(B) = B_(0)hat(i)` with a velocity `vec(v) = v_(0)hat(j)`. The speed of the particle will become `2v_(0)` after a time
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface . A unifrom magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed throught the red it accquire an initnal velocity on the surface , then q is equal to
View SolutionChoose the correct option:
A particle of charge per unit mass `alpha` is released from origin with a velocity `vecv=v_(0)hati` in a magnetic field
`vec(B)=-B_(0)hatk` for `xle(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
and `vec(B)=0` for `xgt(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
The `x`-coordinate of the particle at time `t((pi)/(3B_(0)alpha))` would be
View SolutionLet current `i=2A` be flowing in each part of a wire frame as shown in Fig. 1.138. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field ` B= 4 T` acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is
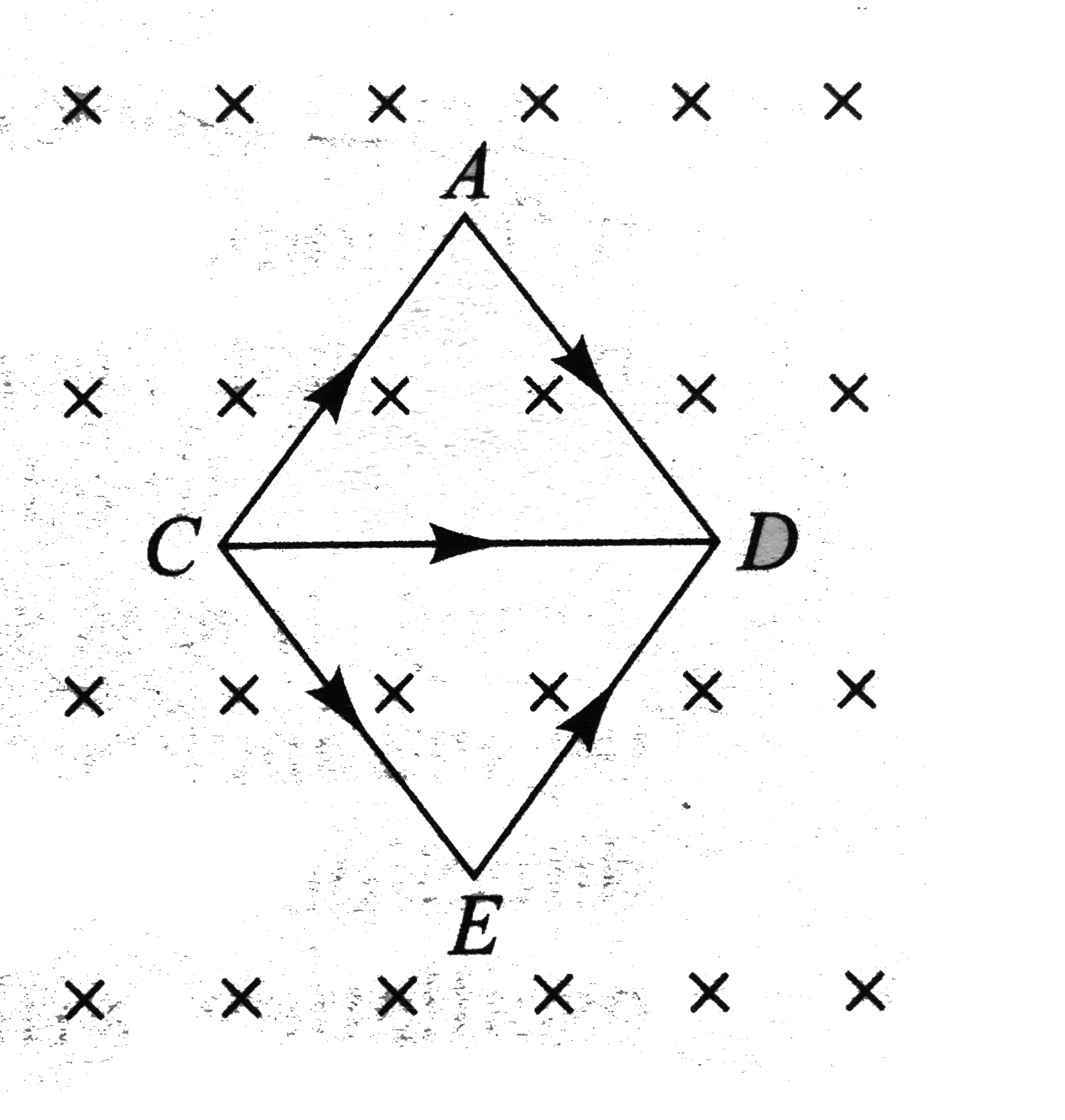
View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of `45^(@)` with the magnetic field . The pitch of the helical path followed by the particles is `rho` . The radius of the helix will be
View SolutionA charge praticule of sepeific charge (charge/ mass ) `alpha` is realsed from origin at time t=0 with velocity `v= v_(0)(hati+hatj)` in unifrom magnetic fields `B= B_(0)hati`. Co-ordinaties of the particle at time `t = (pi)/(B_(0)alpha)` are
View SolutionTwo identical particles having the same mass m and charges `+q` abnd `-q` separeted by a distance d enter in a unifrom magentic field B directed perpendicular to paper inwards with speeds `v_(1)` and `v_(2)` as shown in figure. The particles will not collide if (Ignore electrosatatic force)

View SolutionThe plane of a rectangular loop of wire with sides 0.05 m and 0.08 m is parallel to a uniform magnetic field of induction `1.5 xx 10^-2 T.` A current of 10.0 ampere flows through the loop. If the side of length 0.08 m is normal and the side of length 0.05 m is parallel to the lines of induction, then the torque acting on the loop is
View SolutionA loop of flexible conducting wire of length l lies in magnetic field B which is normal to the plane of loop. A current l is passed through the loop. The tension developed in the wire to open up is
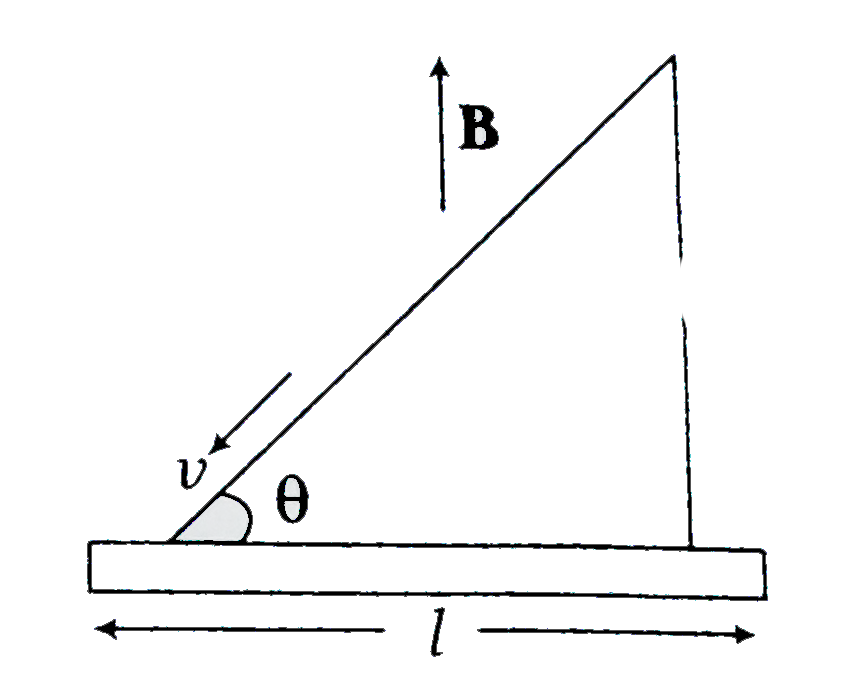
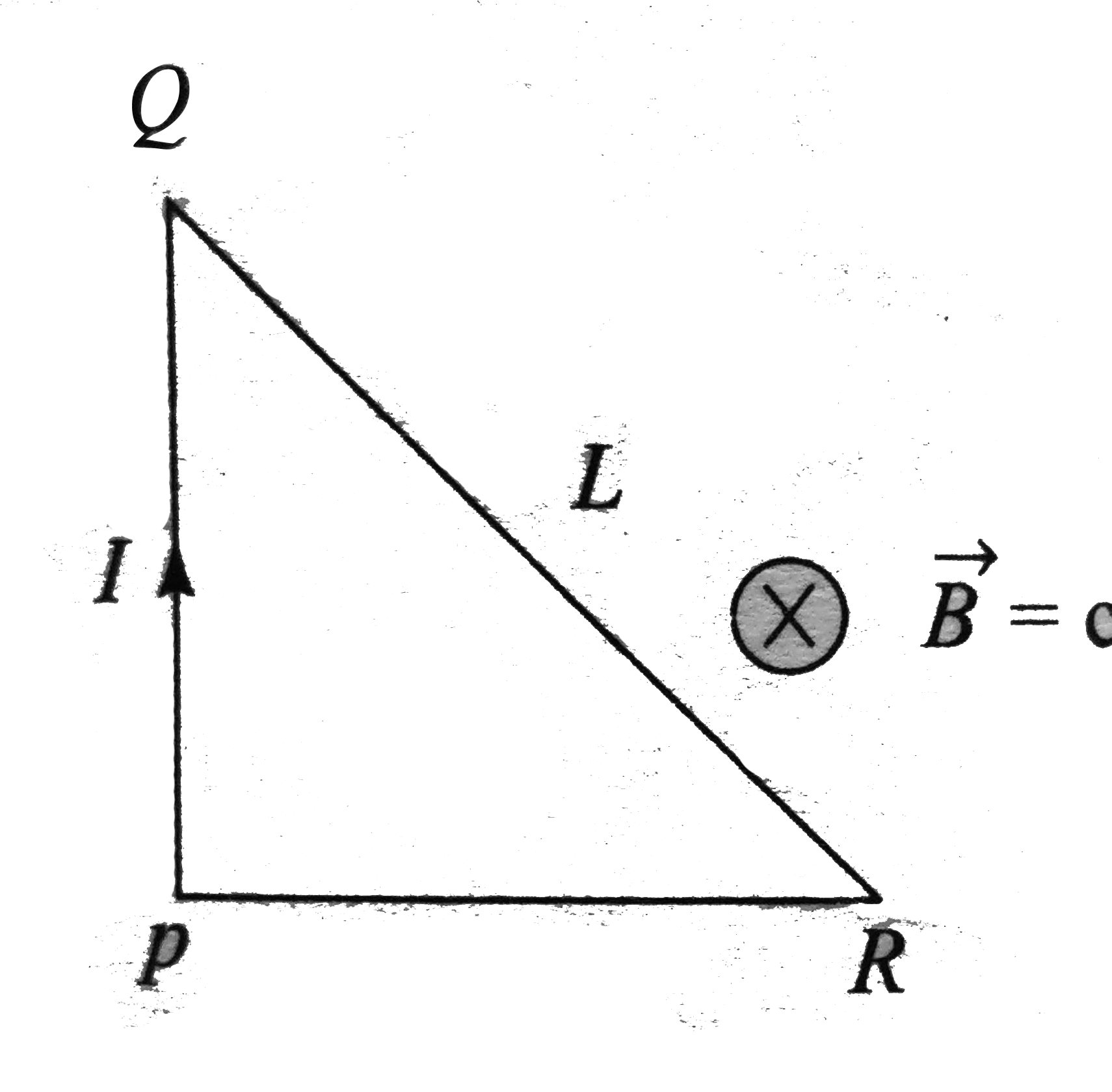
View SolutionA conducting rod of length and mass m is moving down a smooth inclined plane of inclination `theta` with constant velocity V. A current I is flowing in the conductor in a direction perpenducular to paper inwards.A veticallly upwards magnetic fleld B exists in space.Then find magnitude of magnetic field b
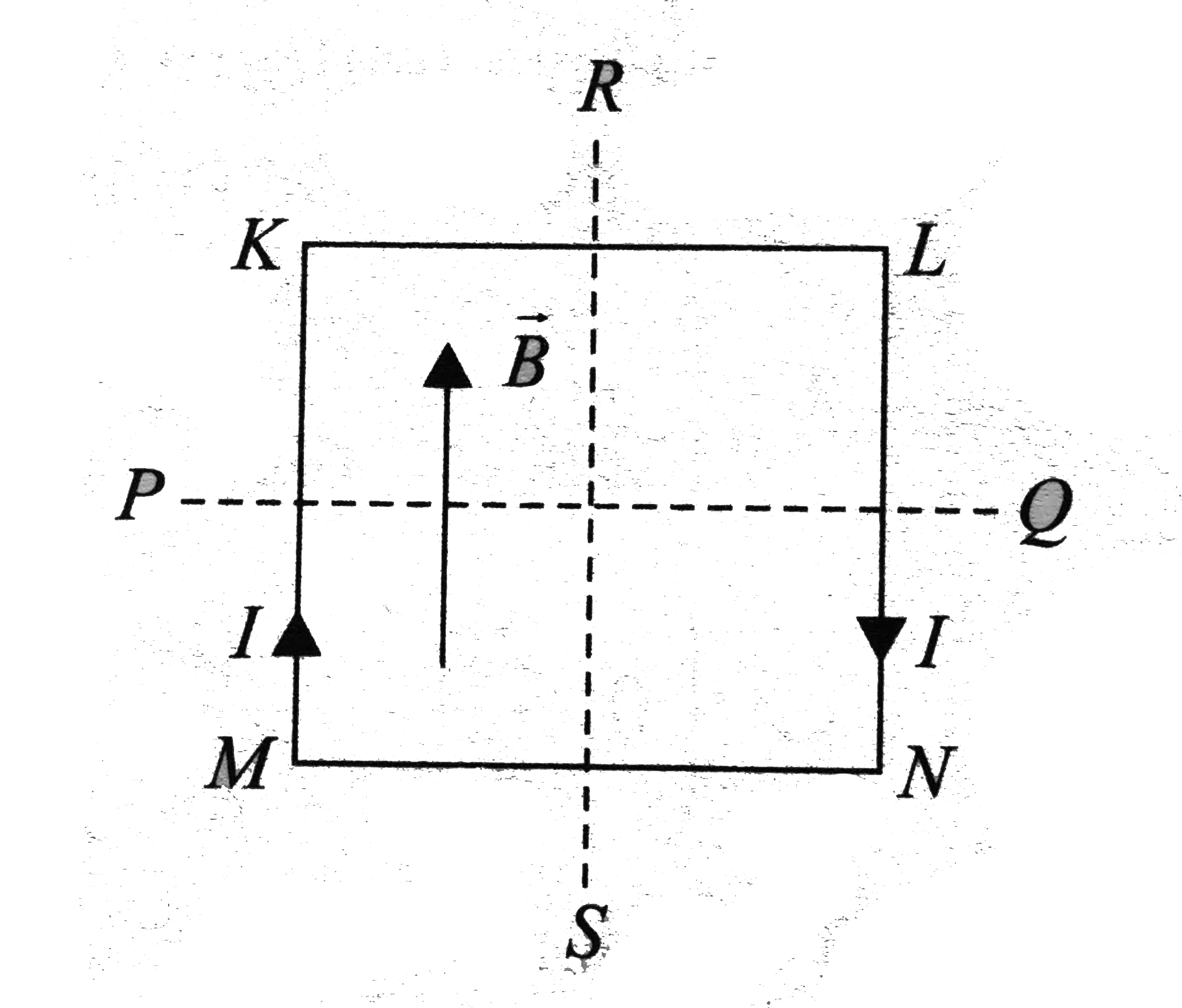
View SolutionA square loop of wire carrying current I is lying in the plane of paper as shown in Fig. 1.141. The magnetic field is present in the region as shown. The loop will tend to rotate
View SolutionA uniform current carrying ering of mass `m` and radius `R` is connected by as massless string as shown. A uniform megnetic field `B_0` exists in the region to keep the ring in horizontal position, then the current in the ring is
View SolutionA circular coil having mass m is kept above the ground (x-z plane) at show height . Coil carries a curretn i in the direaction shown is figure. In which direaction a unifrom magnetic field B be applied so that the magnetic force balances the weight of the coil
View SolutionA charged particle moving along positive x-direction with a velocity v enters a region where there is a uniform magnetic field `B=-hatk`, from `x=0` to `x=d.` The particle gets deflected at an angle `theta` its initial path. The specific charge of the particle is
View SolutionIn the figure shown a coil of single turns is would on a sphere of radius R and mass m .The palne the coil is parallel to the planes and lies in the equatorial plane of the sphere . Current in the coil is i. The vaule of B if the sphere is in equailibrum is

View SolutionThree paticles, an electron (e), a proton (p) and a helium atom (He) are moving in circular paths with constant speeds in the x-y plane in a region where a uniform magnetic field B exists along z-axis. The times taken by e, p and He inside the field to complete one revolution are `t_e, t_p and t_He` respectively. Then,
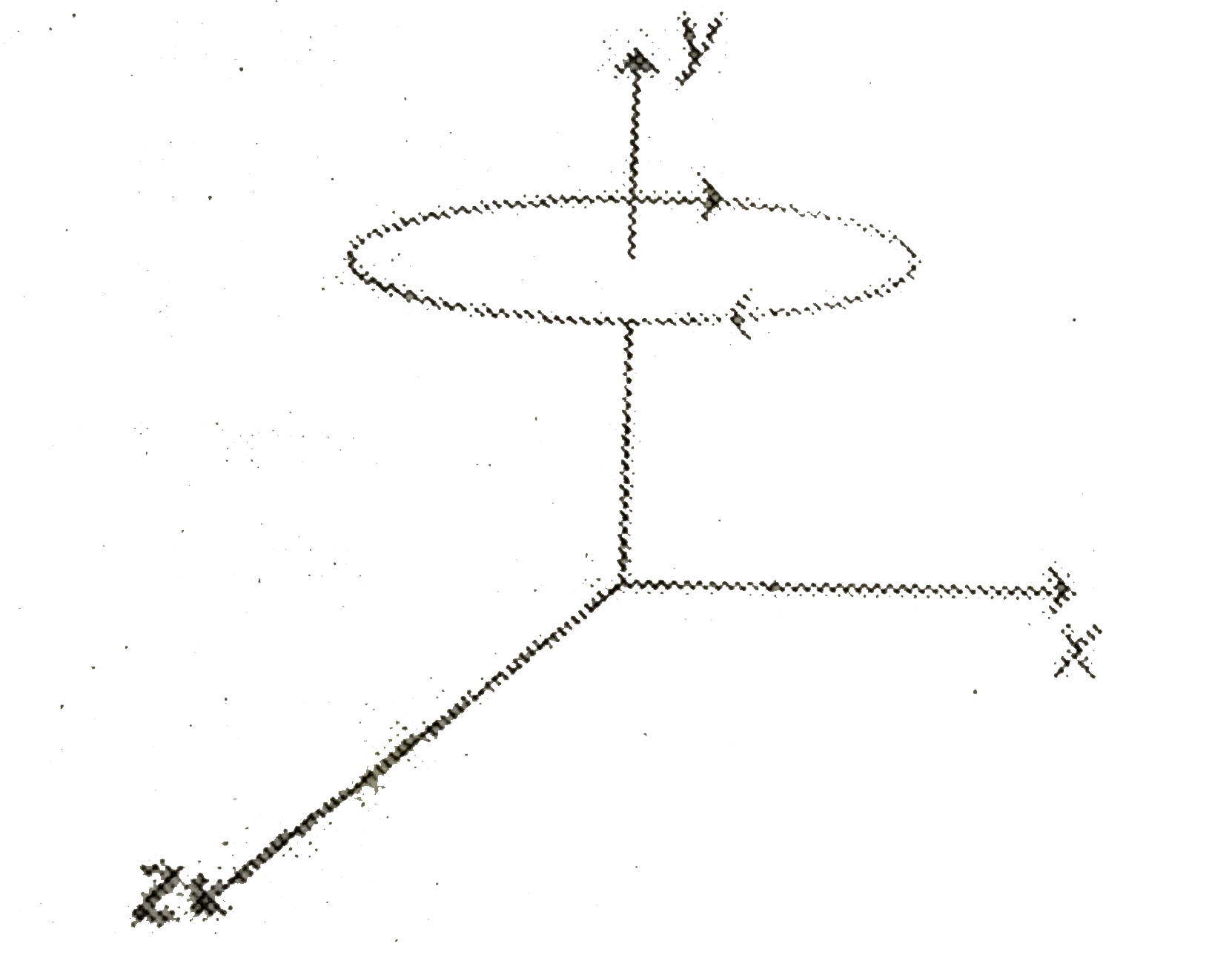
View SolutionThe rigid conducting thin wire frame carries an electric current I and this frame is inside a uniform magnetic field `vec B` as shown in Fig. 1.146. Then,
View SolutionFigure. shows a conducting loop ABCDA placed in a uniform magnetic field (strength B) perpendicular to its plane. The part ABC is the (three-fourth) portion of the square of side length l. The part ADC is a circular arc of radius R. The points A and C are connected to a battery which supplies a current I to the circuit. The magnetic force on the loop due to the field B is

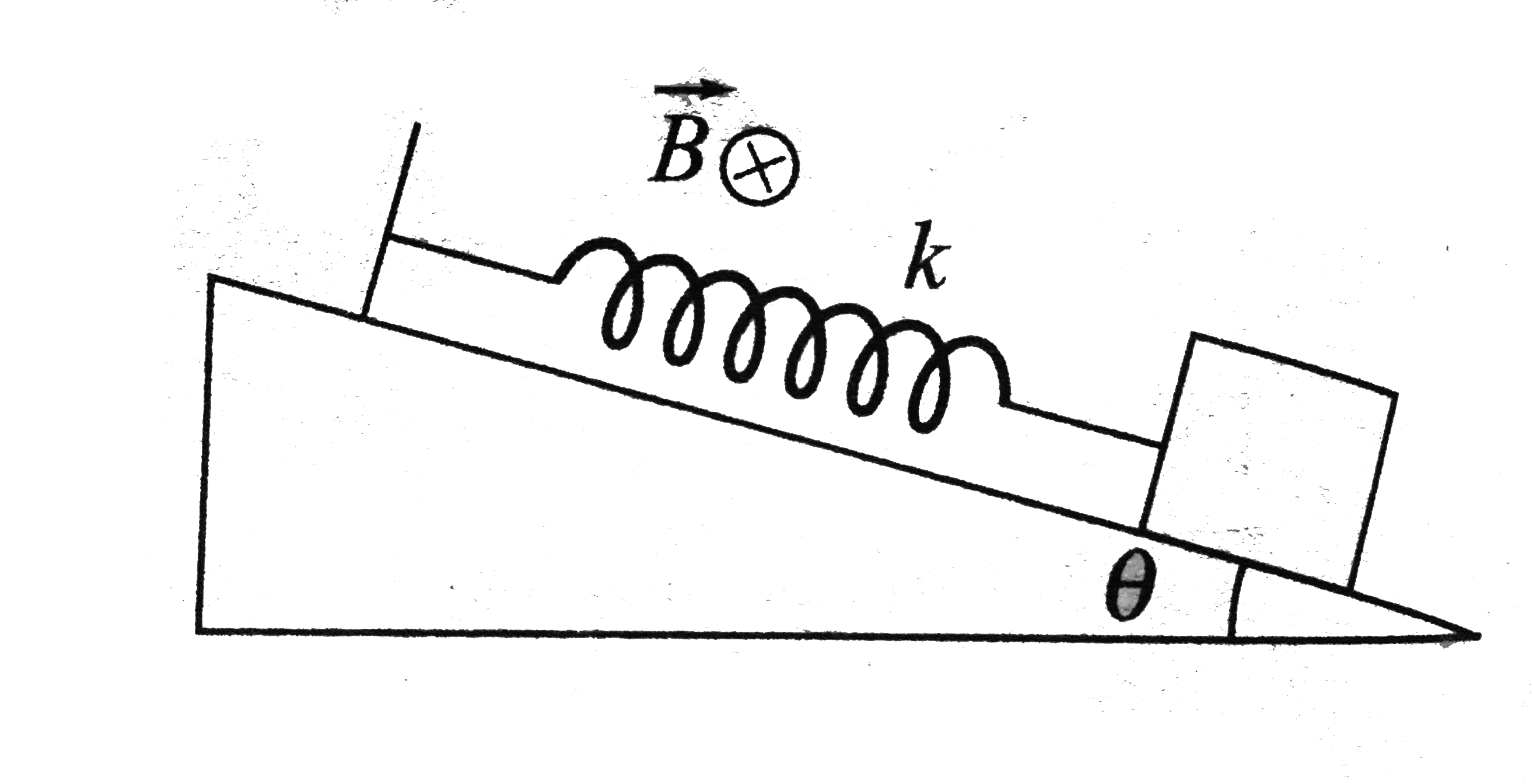
View SolutionA small block of mass m, having charge q, is placed on a frictionless inclined plane making an angle `theta` with the horizontal. There exists a uniform magnetic field B parallel to the inclined plane but perpendicular to the length of spring. If m is slightly pulled on the incline in downward direction, the time period of oscillation will be (assume that the block does not leave contact with the plane)
View SolutionA uniform conducting rectangular loop of sides l, b and mass m carrying current i is hanging horizontally with the help of two vertical strings. There exists a uniform horizontal magnetic field B which is parallel to the longer side of loop. The value of tension which is least is

View SolutionA particle of specific charge `q/m = pi C kg^-1` is projected from the origin toward positive x-axis with a velocity of `10 ms^-1` in a uniform magnetic field `vec B = -2 hat k T.` The velocity `vec v` of particle after time `t=1/12 s` will be (in `ms^-1`)
View SolutionIn Fig. there is a uniform conducting structure in which each small square has side a. The structure is kept in a uniform magnetic field B. Then the magnetic force on the structure will be

View SolutionA charged particle moves insides a pipe which is bent as shown in Fig. 1.151. If `Rlt (mv)/(qB)` , then force exerted by the pipe on charged particle at P is (Neglect gravity)
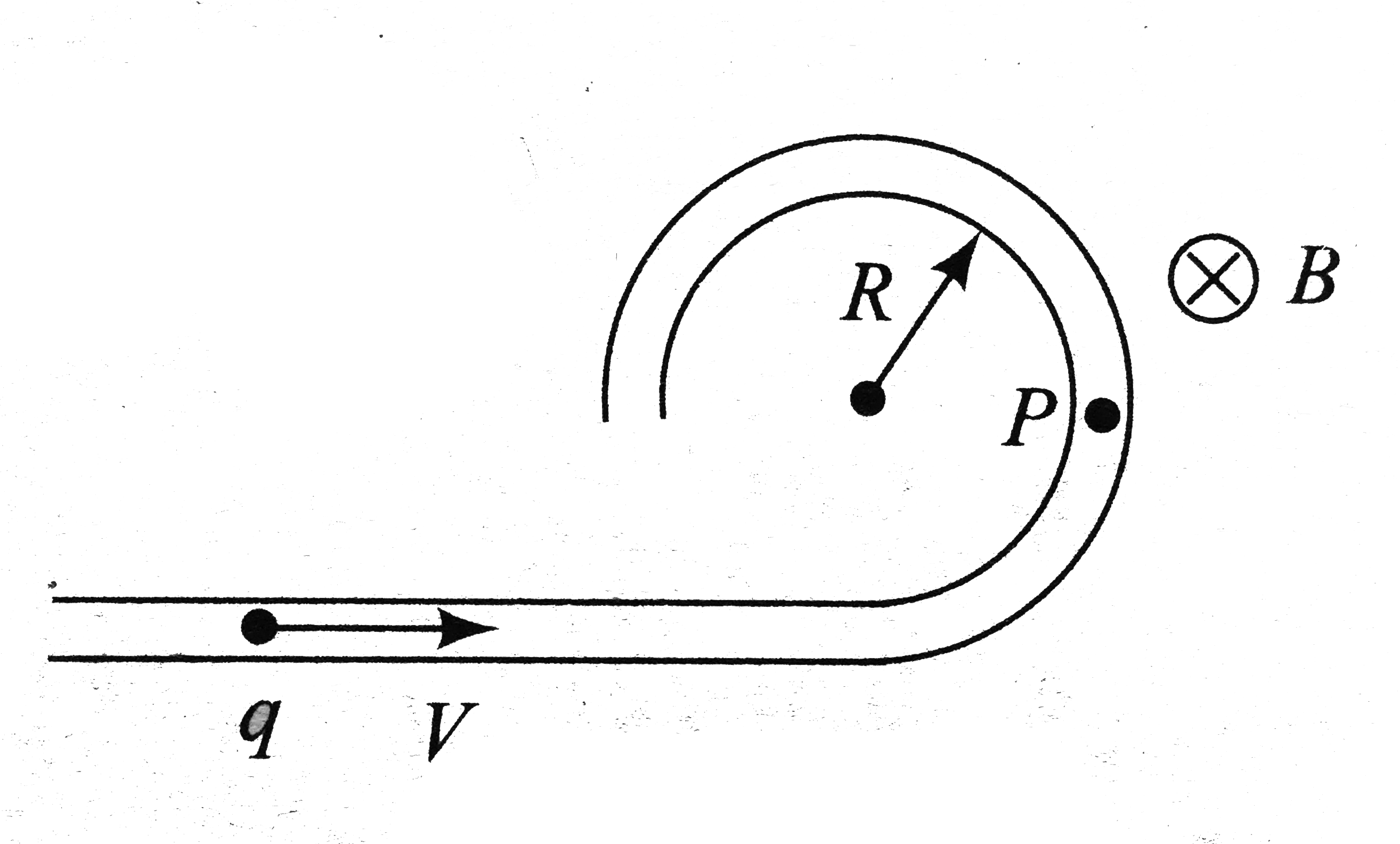
View SolutionConsider a hypothetic spherical body. The body is cut into two parts about the diameter. One of hemispherical portion has mass distribution m while the other portion has indentical charge distribution q. The body is rotated about the axis with constant speed `omega.` Then, the ratio of magnetic moment to angular momentum is
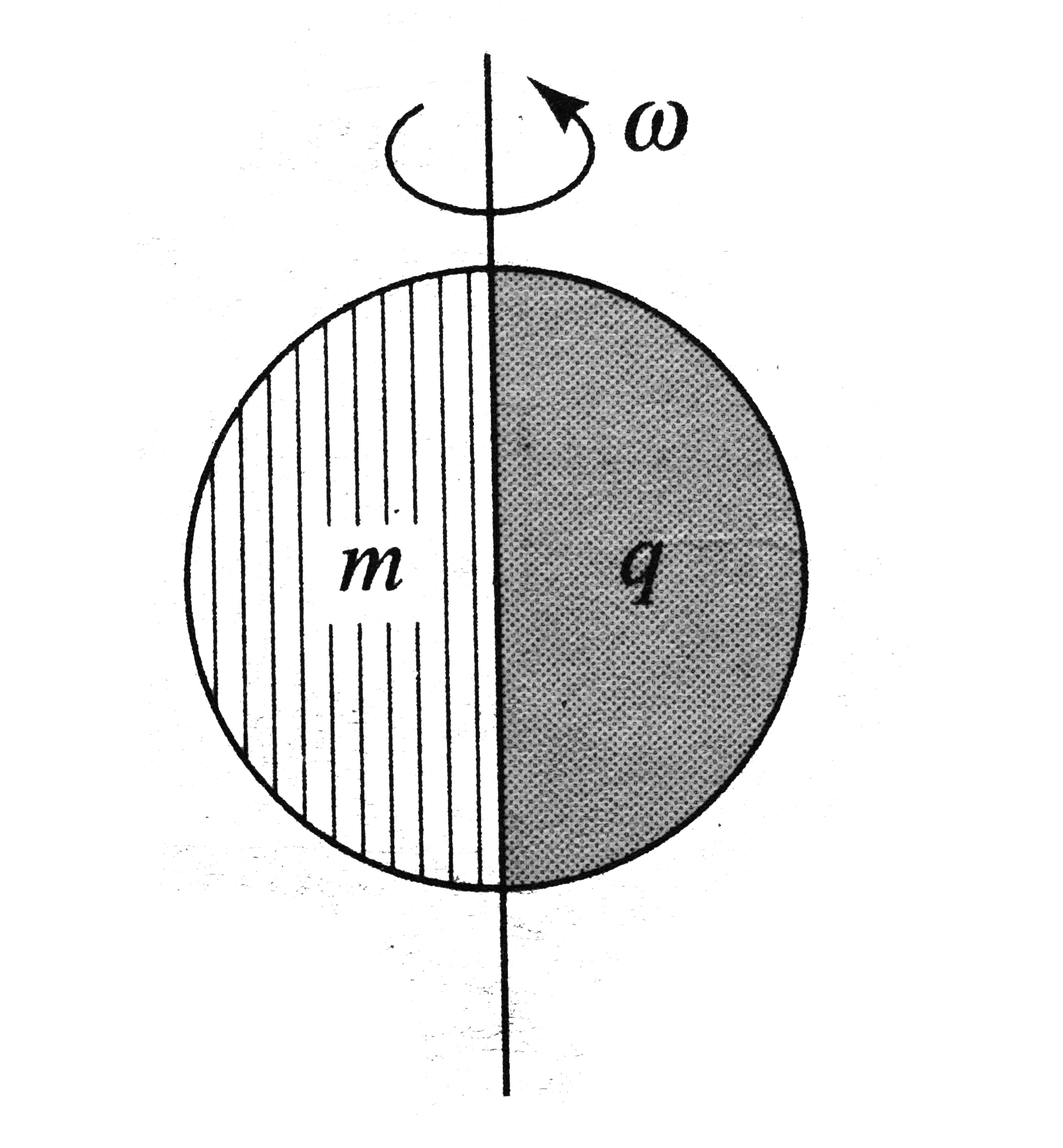
View SolutionAn electron and a proton each travel with equal speeds around circular orbits in the same uniform magnetic field as indicated (not to scale) in Fig. The field is into the page on the diagram. The electron travels ____ arount the _____circle.

View SolutionIn a region of space, a uniform magnetic field B exists in the x-direction. An electron is fired from the origin with its initial velocity u making an angle `alpha` with the y direction in the y-z plane. In the subsequent motion of the electron,

View SolutionIf a charged particle of charge to mass ratio `(q/m) = alpha` centers in a magnetic field of strength B at a speed `v=(2 alpha d) (B),` then

View SolutionA conducting ring of mass 2kg and radius `0.5m` is placed on a smooth plane. The ring carries a current of `i=4A`. A horizontal magnetic field `B=10 T` is switched on at time `t=0` as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is

View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and `1Vm^-1` respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity `1ms^-1` along x-axis and is at origin at t=0. Then, the coordinates of the particle at time `pis` will be
View SolutionA uniform magnetic field exist in a region which forms an equilateral triangle of side a. The magnetic field is perpendicular to the plane of the triangle . A charged q enters into this magnetic field perpendicular to a side with speed v. The charge enters from midpoint and leaves the field from midpoint of other side. Magnetic induction in the triangles is
View SolutionA particle of positive charge q and mass m enters with velocity `Vhatj` at the origin in a magnetic field `B(-hatk)` which is present in the whole space. The charge makes a perfectely inelastic collision with an identical particle (having same charge) ar rest but free to move at its maximum positive y-coordinate. After collision, the combined charge will move on trajectory where `r=(mV)/(qB)`.
View SolutionIn the plane mirror, the coordinates of image of a charged particle (initially at origin as shown in fig. after two and a half time periods are (initial velocity of charge particle `v_0` in the x-y plane and the plane mirror is perpendicular to the x-axis. A uniform magnetic field `Bhati` exists in the space. `P_0` is pitch of helix, `R_0` is raduis of helix.)

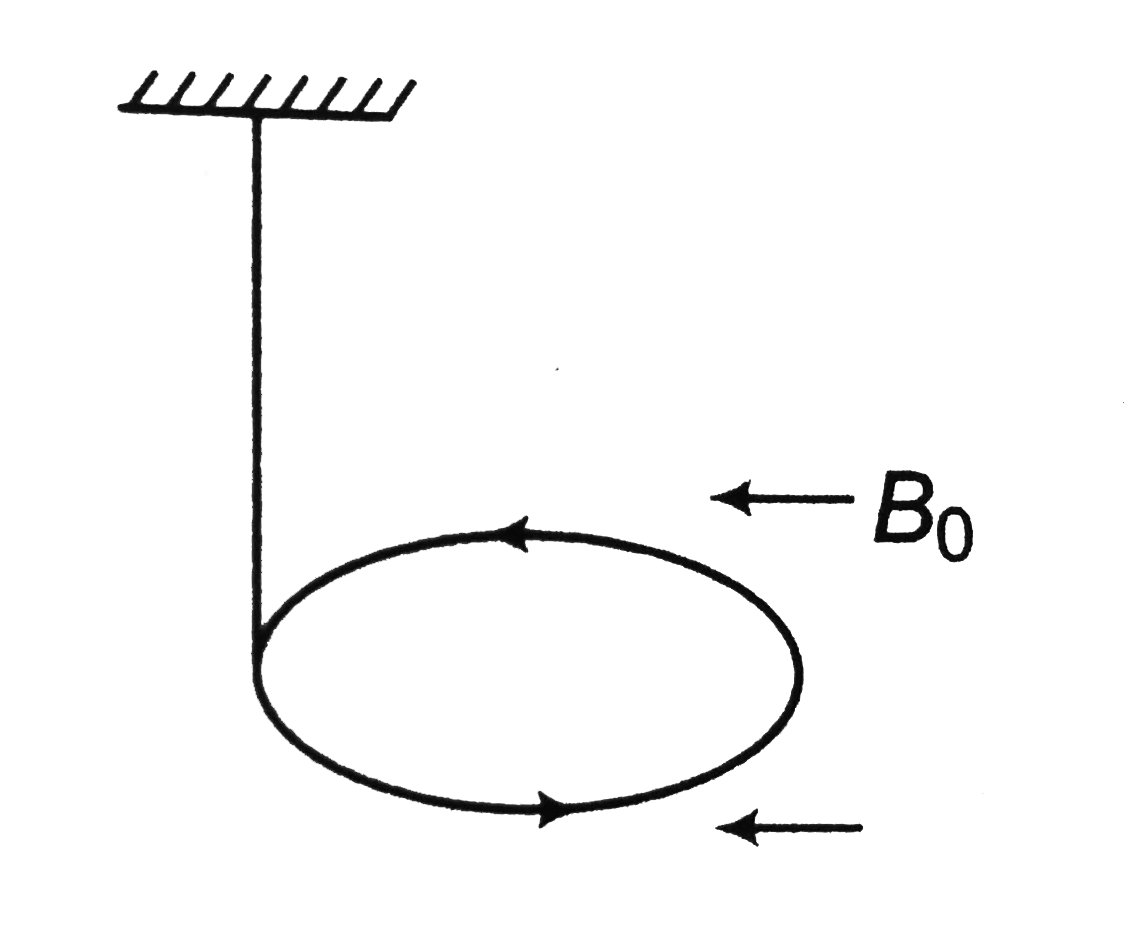
View SolutionA uniform magnetic field of 1.5T exists in a cylinderical region of radius 10.0 cm, its direction being parallel to the axis along east to west. A current carrying wire in north-south direction passes through this region. The wire intersects the axis and experience a force of 1.2N downwards. If the wire is turned from north south to northest-southwest direction. then magnitude and direction of force is
View SolutionAn insulating rod of length I carries a charge q distrubuted uniformly on it. The rod is pivoted at its mid-point and is rotated at a frequency f about a fixed axis perpendicular to the the rod and passing through the pivot . The magnetic moment of the rod system is
View SolutionTwo straight segments of wire ab and bc each carrying current I, are placed as shown in fig. The cube edge is 50 cm and magnetic field is uniform along y-axis having magnitude 0.4T. If I=3A, the force experienced by the wire abc in the presence of magnetic field

View SolutionA current carrying loop is placed in the non-uniform magnetic field whose variation in space is shown in fig. Direction of magnetic field is into the plane of paper. The magnetic force experienced by the loop is
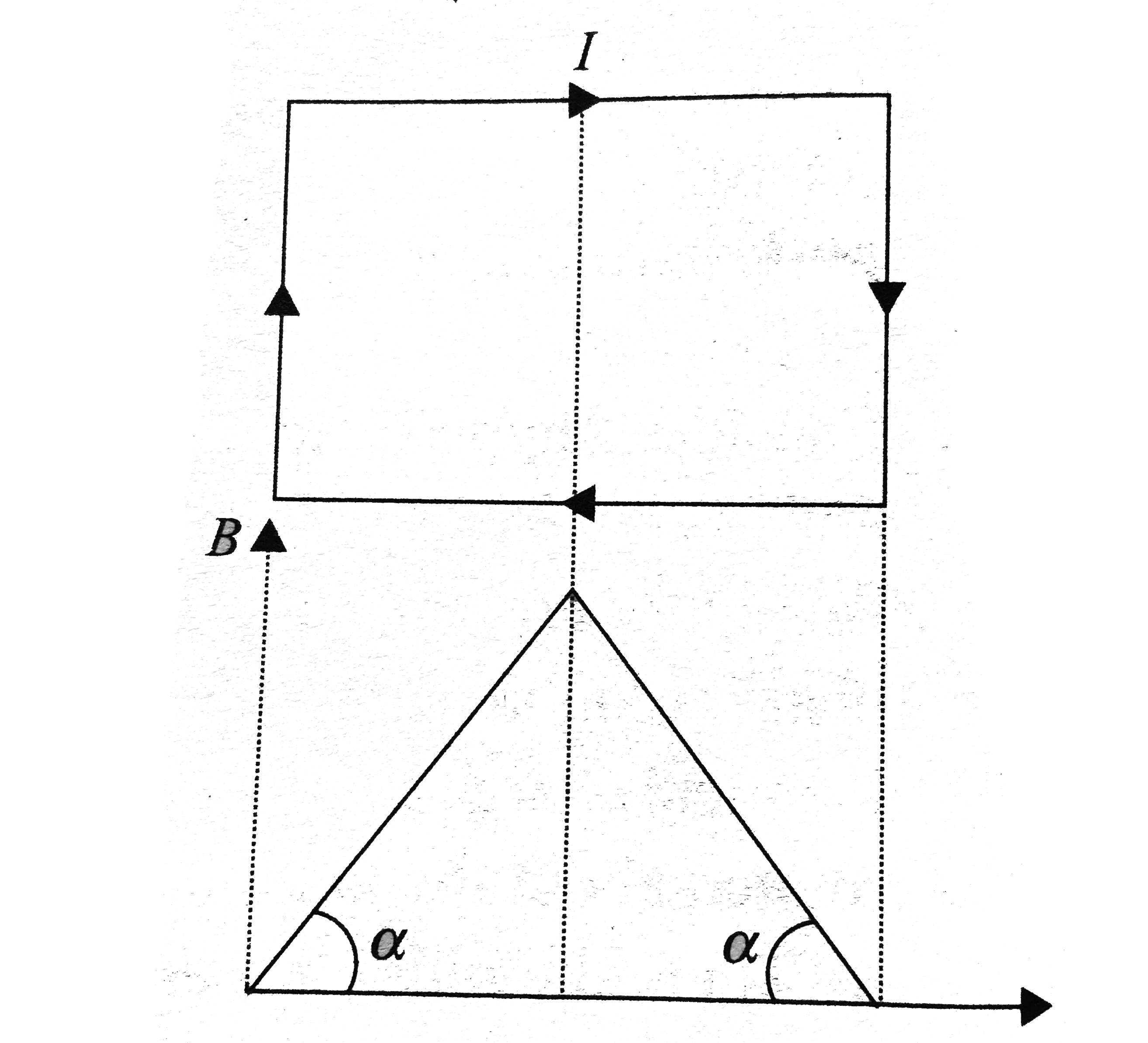
View SolutionA current carrying loop lies on a smooth horizontal plane. Then,
View SolutionA semicircular wire of radius R, carrying current I, is placed in a magnetic field as shown in Fig. On left side of X'X, magnetic field strength `B_0`. On right side of X'X, magnetic field strength `2B_0`Both fields are directed inside the page. The magnetic force experienced by the wire would be

View SolutionA wire of cross-sectional area A forms three sides of a square and is free to rotate about axis OO'. If the structure is deflected by an angle `theta` from the vertical when current i is passed through it in a magnetic field B acting vertically upward and density of the wire is `rho`, then the value of `theta` is given by

View SolutionA proton of mass `1.67xx10^(-27)` kg charge `1.6xx10^(-19) C` is projected in xy-plane with a speed of `2xx10^(6) m//s` at an angle of `60^(@)` to the X-axis. If a uniform magnetic field of 0.14 T is applies along the Y-axis, then the path of the proton is
View SolutionA beam of mixture of `alpha` particle and protons are accelerted through same potential difference before entering into the magnetic field of strength B. if `r_1=5` cm then `r_2` is

View SolutionAn electron is projected at an angle `theta` with a uniform magnetic field. If the pitch of the helical path is equal to its radius, then the angle of projection is
View SolutionA charged particle moves in a uniform magnetic field perpendicular to it, with a radius of curvature 4 cm. On passing through a metallic sheet it loses half of its kinetic energy. Then, the radius of curvature of the particle is
View SolutionA particle of specific charge `alpha` is projected from origin with velocity `v=v_0hati-v_0hatk` in a uniform magnetic field `B=-B_0hatk`. Find time dependence of velocity and position of the particle.
View SolutionA straight peice of conducting wire with mass M and length L is placed on a frictionless incline tilited at an angle `theta` from the horizontal (as shown in fig) There is a uniform. Vertical magnetic field at all points (produced by an arrangement of magnets not shown in fig. To keep the wire from sliding down the incline, a voltage source is

attached to the ends of the wire. When just the right amount of current flows through the wire, the wire remains at rest. Determine the magnitude and direction of the current in the wire that will cause the wire to remain at rest.
View SolutionIn a moving coil galvanometer is based on the
View SolutionIn a moving coil galvanometer, we use a radial magnetic field so that the galvanometer scale is
View SolutionThe current that must flow through the coil of a galvanometre so as to produce a deflection of one division on its scale is called
View SolutionIn a moving coil galvanometer, the deflection of the coil `theta` is related to the electrical current I by the relation
View Solution
Exercises Single Correct questions and complete solutions for chapter MAGNETIC FIELD AND MAGNETIC FORCES of CENGAGE PHYSICS (ENGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS MAGNETIC FIELD AND MAGNETIC FORCES
- Archives Assertion-reasion
- Archives Comprehension
- Archives Fill In The Blank
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives True /false
- Comphension Based
- Comprehension type
- Exercise 1.1
- Exercise 1.2
- Exercise1.3
- Exercises Assertion -reasoning
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises Subjective
- Illustration
- Multiple
- Multiple Correct Answer type
- Single Correct Answer Type
- Solved Example
- Subjective
- Subjective type