Complete Solutions to Solved Example of chapter MAGNETIC FIELD AND MAGNETIC FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD AND MAGNETIC FORCES |
| CENGAGE PHYSICS | Solved Example |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
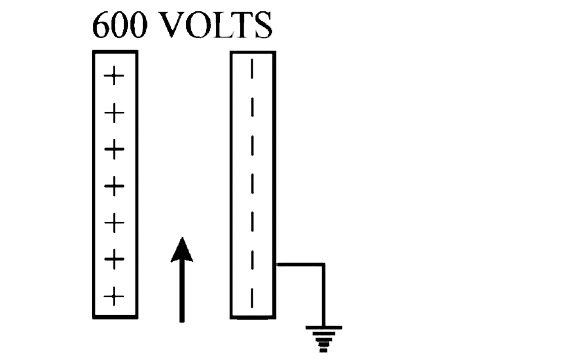
A potential difference of `600 volts` is applied across the plates of a parallel plate consenser . The separation between the plates is `3mm`. An electron projected vertically, parallel to the plates , with a velocity of `2 xx 10^(6) m//sec` moves underflected between the plates. Find the magnitude and direction of the magnetic field in the region between the condenser plates. ( Neglect the edge effects). ( Charge of the electron `= -1.6xx10^(-19) coulomb)
View SolutionA particle of mass `1xx 10^(-26) kg` and charge `+1.6xx 10^(-19) C` travelling with a velocity `1.28xx 10^6 ms^-1` in the `+x` direction enters a region in which uniform electric field E and a uniform magnetic field of induction B are present such that `E_x = E_y = 0, E_z= -102.4 kV m^-1, and B_x = B_z =0, B_y = 8xx 10^-2.` The particle enters this region at time `t=0.` Determine the location (x,y,z coordinates) of the particle at `t= 5xx10^-6 s.` If the electric field is switched off at this instant (with the magnetic field present), what will be the position of the particle at `t= 7.45xx10^-6 s` ?
View SolutionA particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

View SolutionA beam of proton with a velocity of `4xx10^(5)ms^(-1)` enters a uniform magnetic field of 0.3 T at an angle of `60^(@)` to the magnetic field/The radius of helical path taken by proton beam is
View SolutionAn electron gun `G` emits electons of energy `2 keV` travelling in the positive x-direction. The electons are required to hit the spot `S` where `GS=0.1 m`, and the line `GS` makes an angle of `60^@` with the x-axis as shown in figure. A uniform magnetic field `B` parallel to `GS` exists in the region outside the electron gun.

find the minimum value of `B` needed to make the electrons hit `S`.
View SolutionAn electron in the ground state of hydrogen atom is removing in unanticlockwise direction in a circle orbit of radius `R`

a. Obtain an expression for the orbital magnetic dipole moment of the electron .
b. The atom is placed in a uniform magnetic indution `bar B` such that the plane normal to the electron orbitmakes an angle of `30^(@)` with the magnetic induction. Find the tarque experienced by the orbiting electron .
View SolutionA particle of mass m and charge q is moving in a region where uniform, constant electric and mangetic fields `vec E and vec B` are present. `vec E and vec B` are parallel to each other. At time `t=0,` the velocity `vec v_0` of the particle is perpendicular to `vec E` (Assume that its speed is always `lt lt c`, the speed of light in vacuum). Find the velocity `vec v` of the particle at time `t`. You must express your answer in terms of `t, q, m,` the vector `vec v_0, vec E` and `vec B` and their magnitudes `vec v_0, vec E` and `vec B`.
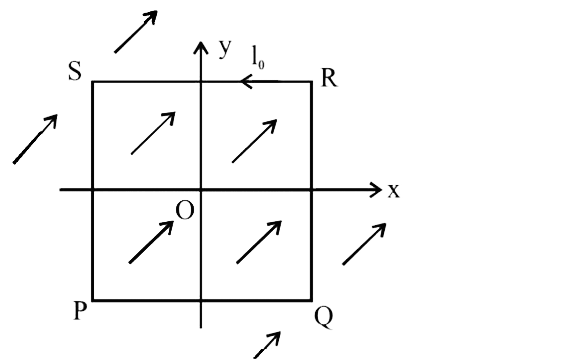
View SolutionA uniform constant magnetic field `B` is directed at an angle of `45^(@)` to the `x axis` in the ` xy`- plane . ` PQRS` is a rigid, square wire frame carrying a steady current `I_(0)`, with its centre at the origin `O`. At time ` t = 0`, the frame is at rest in the position as shown in figure , with its sides parallel to the ` x and y` axis. Each side of the frame is of mass `M` and length `L`.
(a) What is the torque `tau` about `O` acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time `Deltat`, and the axis about this rotation occurs .`( Deltat is so short that any variation in the torque during this interval may be neglected .) Given : the moment of interia of the frame about an axis through its centre perpendicular to its about an axis through its centre perpendicular to its plane is `(4)/(3) ML^(2)`.
View SolutionThe region between `x=0` and `x=L` is filled with uniform steady magnetic field `B_0hatk`. A particle of mass m, positive charge q and velocity `v_0hati` travels along x-axis and enters the region of the magnetic field. Neglect the gravity throughout the question.
a. Find the value of `l` if the particle emerges from the region of magnetic field with its final velocilty at an angel `30^@` to its initial velocity.
b. Find the final velocity of the particle and the time spent by it in the magnetic field, if themagnetic field now extends upto 2.1`L`.
View SolutionA rectangular loop `PQRS` made from a uniform wire has length a, width `b` and mass `m`.It is free to rotate about the arm `PQ` which remasins hinged along a horizontal line taken as the y-axis (see figure). Take the vertically upward direction as the z-axis. A uniform magnetic fiedl `B=(3hati+3hatk)B_0` exists in the region. The lop is held in the xy-plane and a current `I` is passed through it. The loop in now released and is found to stay in the horizontal position in equilibrium.
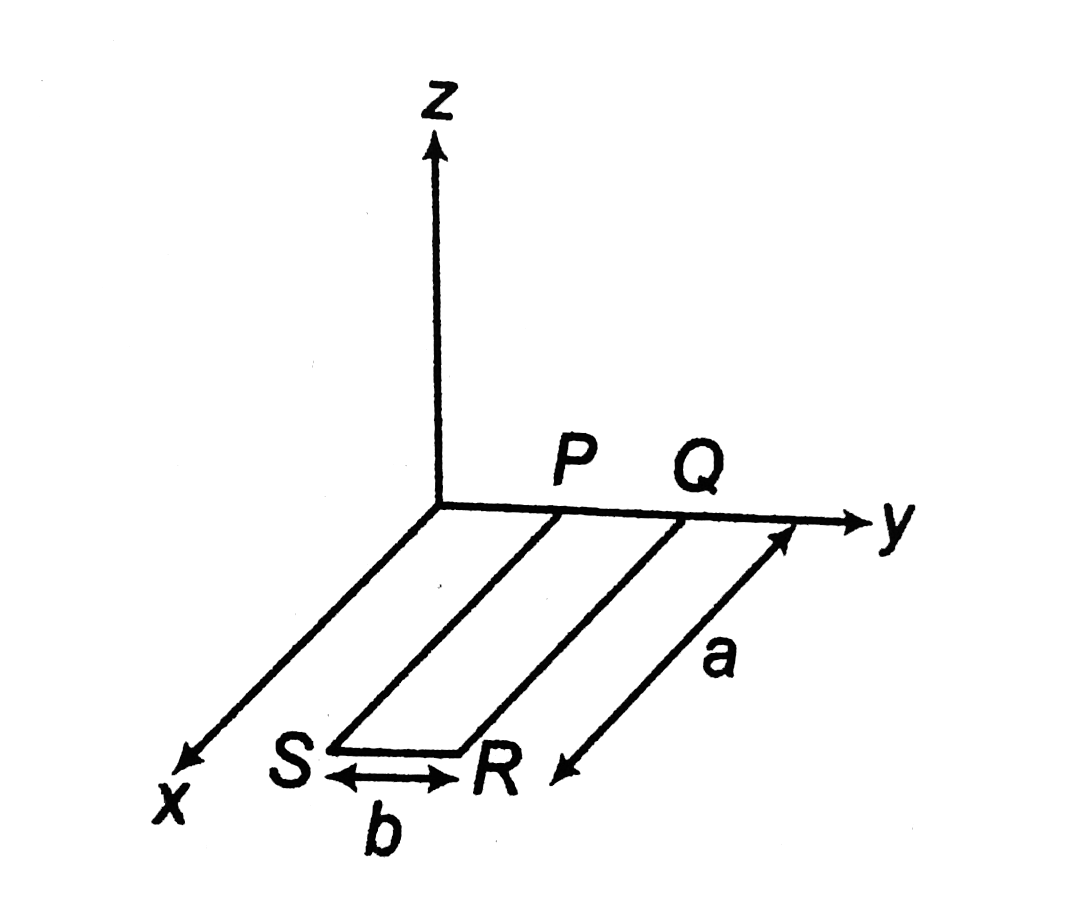
a. What is the direction of the current `I` in `PQ`?
b. Find the magnetic force on the arm `RS`.
c. Find the expression for I in terms of `B_0`, a, b` and m`.
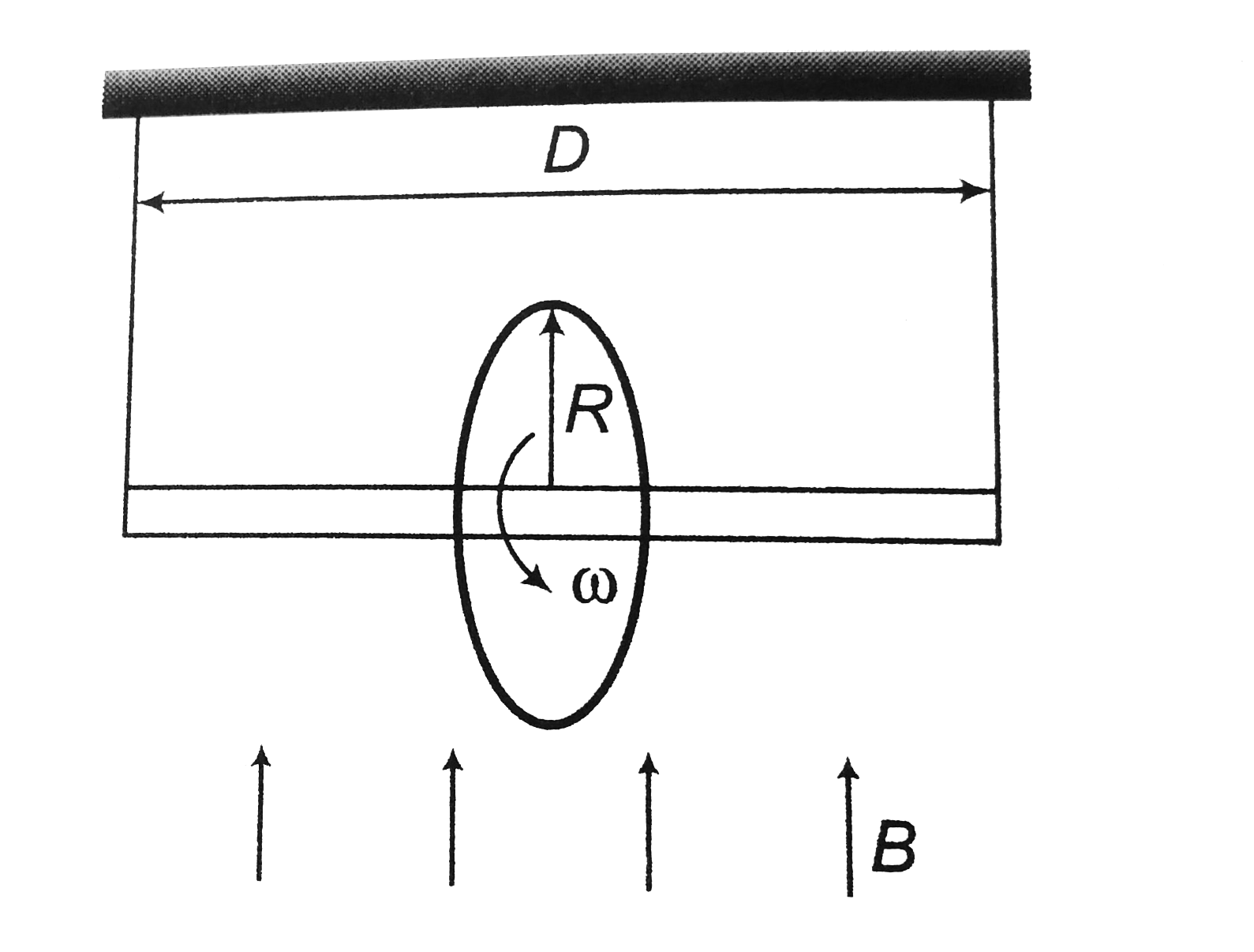
View SolutionA ring of radius `R` having uniformly distributed charge `Q`. is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is `T_0`. Now, a vertical magnetic field is switched on and ring is rotated at constant angular velocity co. Find the maximum value of co h which the ring can be rotated if the strings can withstand a maximum tension of `(3T_0)/2`
View SolutionIn a moving coil galvanometer, torque on the coil can be experessed as `tau = ki`, where `i` is current through the wire and `k` is constant . The rectangular coil of the galvanometer having number of turns `N` , area `A` and moment of interia `I` is placed in magnetic field `B`. Find
(a) `k` in terms of given parameters `N,I,A andB`
(b) the torsion constant of the spring , if a current `i_(0)` produces a deflection of `(pi)//(2)` in the coil .
(c) the maximum angle through which the coil is deflected, if charge `Q` is passed through the coil almost instaneously. ( ignore the daming in mechinal oscillations).
View SolutionA slightly divergent beam of charged particles accelerated by a Potential difference V propogates from a point A along the axis of a solenoid. The beam is brought into focus at a distance l from the point A at two successive values of magnetic induction `B_1 and B_2.` Find the specific charge `q//m` of the particles.
View SolutionA small charged ball having mass m and charge q is suspended from a rigid support by means of an inextensible thread of length l. It is made to rotate on a horizontal circular path in a uniform, time independent magnetic field of induction B which is directed upward. The time period of revolution of the ball is `T_0.` If the thread is always stretched, calculate the radius of circular path on which the ball moves.
View SolutionNon-relativistic protons move reactilinearly in the region of space where there are uniform mutually perpendicular electric and magnetic fields with E and B. The trajectory of the protons lie in the plane X-Y as shown in Fig. 1.107 and forms an angle `phi` with X-axis. Find the pitch of the helical trajectory along which the protons will move after the electric field is switched off.

View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction `B` is applied at right angle to the strip.
(a) Calculate the drift velocity `v_d` of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field `E` Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field `E_H` across the conductor until the forces of this electrostatic field `E_H` balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field `E_H`?
Assume that n, the number of conductor electrons per unit volume is `1.1xx10^(29) m^-3, h = 0.02 m, w= 0.1 cm, i = 50 A, and B=2 T.`

View SolutionA straight conductor of weight 1 N and length 0.5 m, is located in a plane making an angle `30^@` with the horizontal so that it is perpendicular to a uniform mangetic field of induction `B= 0.109 T.` Given that the conductor carries a current of 10 A away from the reader, and coefficient of static friction is 0.1, find the force needed to be applied parallel to the plane to sustain the conductor at rest.
View SolutionThere is a constant homogeneous electric field of `100 Vm^-1` within the region `x=0 and x=0.167 m` pointing in x-direction. There is a constant homogeneous mangetic field B within the region `x=0.167 m and x=0.334 m` pointing in the z-direction. A proton at rest at the origin is released in positive x-direction. Find the minimum strength of the magnetic field B, so that the proton is detected back at `x=0, y=0.167 m.` (mass of proton `= 1.67 xx 10^(-27) kg)`
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by `vec E = - E_0 hat k and vec B= -B_0 hat k` , respectively. The particle enters into the field at `(a_0, 0, 0)` with velocity `vec v = v_0 hat j`. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is `mu`. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View SolutionA loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0 T perpendicular to the plane of the loop. Show that when a current as shown in Fig. 1.112 is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 A.

View SolutionA circular coil of 100 turns has an effective radius of 0.05 m and carries a current of 0.1 A. How much work is required to turn it in an external magnetic field of `1.5 Wb m^-2` through `180^@` about an axis perpendicular to the magnetic field. The plane of the coil is initially perpendicular to the magnetic field.
View SolutionA positively charged particle of charge `1 C` and mass `40 g`, is revolving along a circle, of radius `40 cm` with velocity `5 m/s` in a uniform magnetic field with centre at origin 0 in xy-plane. At `t = 0`, the particle was at (`0, 0.4 m, 0`) and velocity was directed along positive x-direction. Another particle having charge `1 C` and mass `10 g` moving uniformly parallel to z-direction 40 with velocity `40/pi m/s`collides with revolving particle at `t = 0` andgets stuck with it. Neglecting `7C` gravitational force and colombians force, calculate `x, y` and `z`-coordinates of the combined particle at `t=pi/40sec`
View SolutionAn electron accelerated by a potential difference `V= 3` volt first enters into a uniform electric field of a parallel plate capacitor whose plates extend over a length `l= 6 cm` in the direction of initial velocity. The electric field is normal to the direction of initial velocity and its strength varies with time as `E= alpha t,` where `alpha= 3600 V m^-1 s^-1.` Then the electron enters into a uniform magnetic field of induction `B = pi xx 10^-9 T.` Direction of magnetic field is same as that of the electric field. Calculate pitch of helical path traced by the electron in the magnetic field. (Mass of electron, `m = 9 xx 10^-31 kg`)
View SolutionA particle having mass m and charge `q` is released from the origin in a region in which ele field and magnetic field are given by `B=-B_0hatj`and `E=E_0hatk`.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View SolutionA non-relativistic charge q of mass m originates at a point A lying on x-axis and moves with velocity v at an angle to the x-axis. A screen is located at a distance l from A. Find the distance r from the x-axis to the point on the screen into which the charge strikes.

View Solution
Solved Example questions and complete solutions for chapter MAGNETIC FIELD AND MAGNETIC FORCES of CENGAGE PHYSICS (ENGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS MAGNETIC FIELD AND MAGNETIC FORCES
- Archives Assertion-reasion
- Archives Comprehension
- Archives Fill In The Blank
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives True /false
- Comphension Based
- Comprehension type
- Exercise 1.1
- Exercise 1.2
- Exercise1.3
- Exercises Assertion -reasoning
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises Subjective
- Illustration
- Multiple
- Multiple Correct Answer type
- Single Correct Answer Type
- Solved Example
- Subjective
- Subjective type