Complete Solutions to Illustration of chapter GEOMETRICAL OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GEOMETRICAL OPTICS |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Show that for a light ray incident at an angle i on getting reflected the angle of deviation is `delta=pi-2i` or `pi +2i`.
View SolutionFor a fixed incident light ray, if the mirror be rotated through and angle `theta` (about an axis which lies in the plane of mirror and perpendicular to the plane of incidence), show that the reflected ray turns through an angle 2`theta` in same sense.
View SolutionFigure. (a)shows an object placed in front of a plane mirror. P,Q and R are the three positions where the image of object may be seen, Observer A is able to see the image at position Q. Where does the observer B see the image of the object?
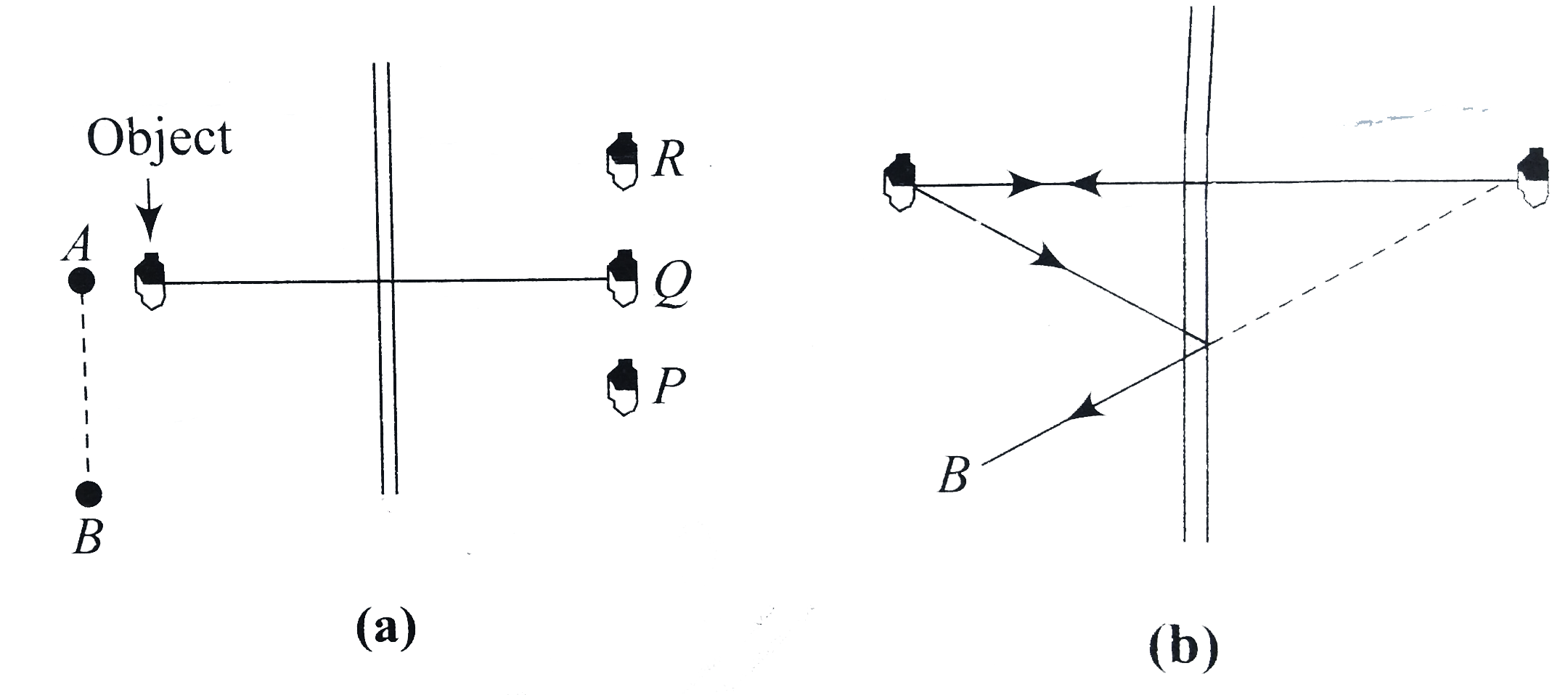
View SolutionA light ray is incident on a plane mirror at an angle of `30^(@)` with horizontal. At what angle with horizontal must a plane mirror be placed in its path so that it becomes vertically upwards after reflection?
View SolutionFigure. Shows a point object A and a plane mirror MN. Find the position of the image of object A, in mirror MN, by drawing ray diagram. Indicate the region in which the observer's eye must be present in order to view the image. (This region is called field of view.)
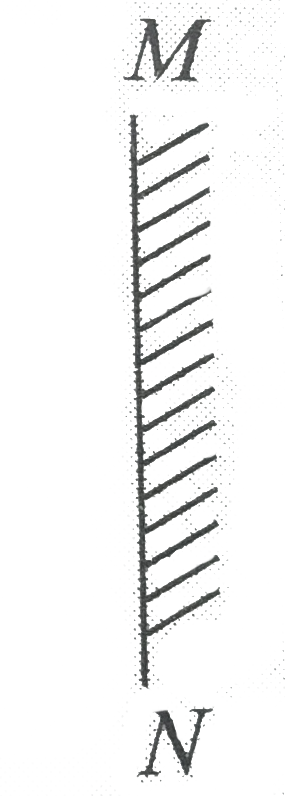
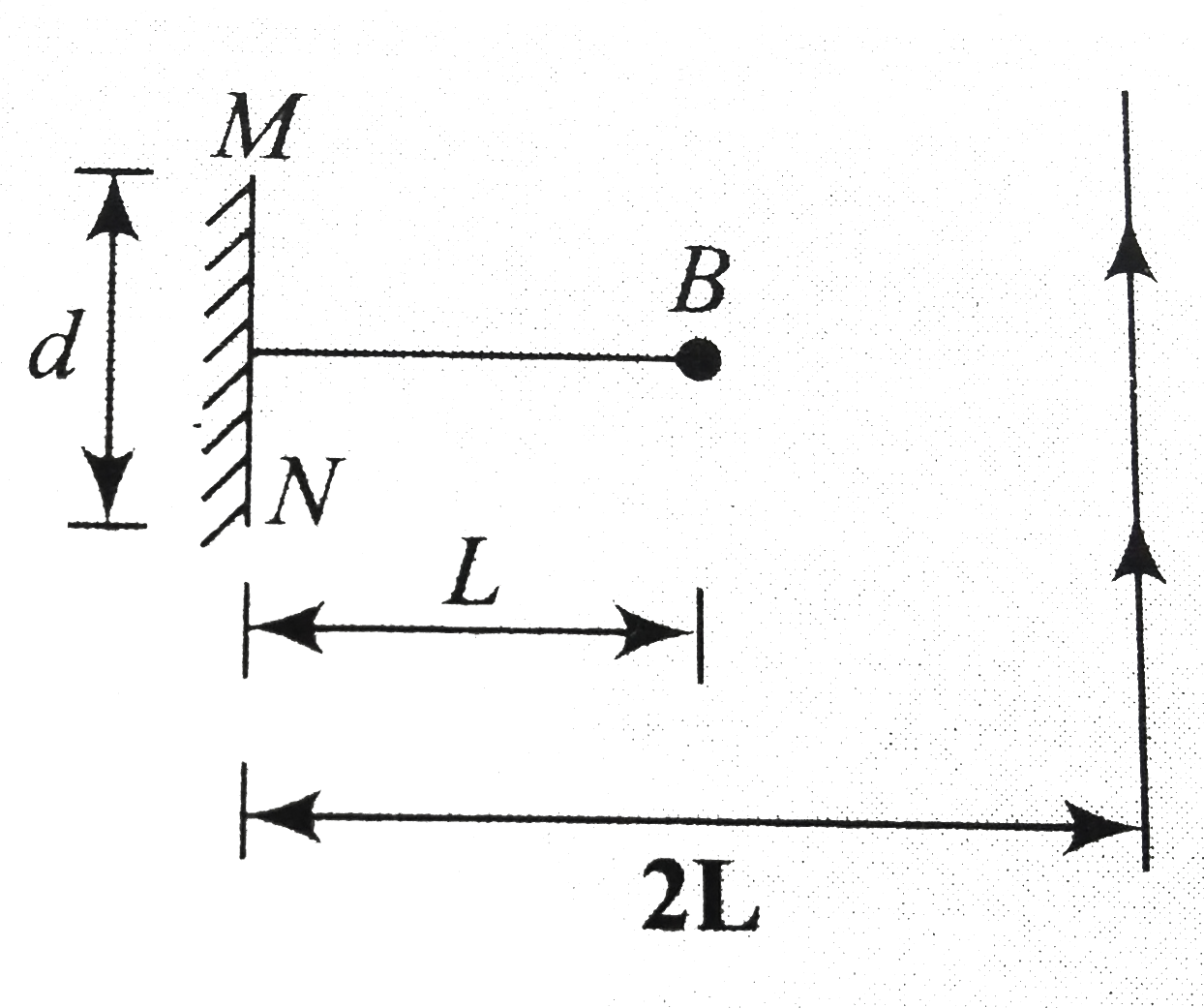
View SolutionA point source of light B is placed at a distance L in front of the center of a mirror of width d hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it, as shown in Fig . Find the greated distance over which he can see the image of the light source form the mirror.
View SolutionShow that the minimum size of a plane mirror required to see the full image of an observer is half the size of that observer.
View SolutionFigure shows a plane mirror and an object that are moving towards each other. Find the velocity of image.

View SolutionConsider two perpendicular mirrors `M_(1)` and `M_(2)` and a point object O. Taking origin at the point of intersection of the mirrors and the coordinates of object as (x,y), find the position and number of images.
View SolutionFind the angle of incidence of the ray shown in Fig. for which it passes through the pole, given that `MI|\|CP`.
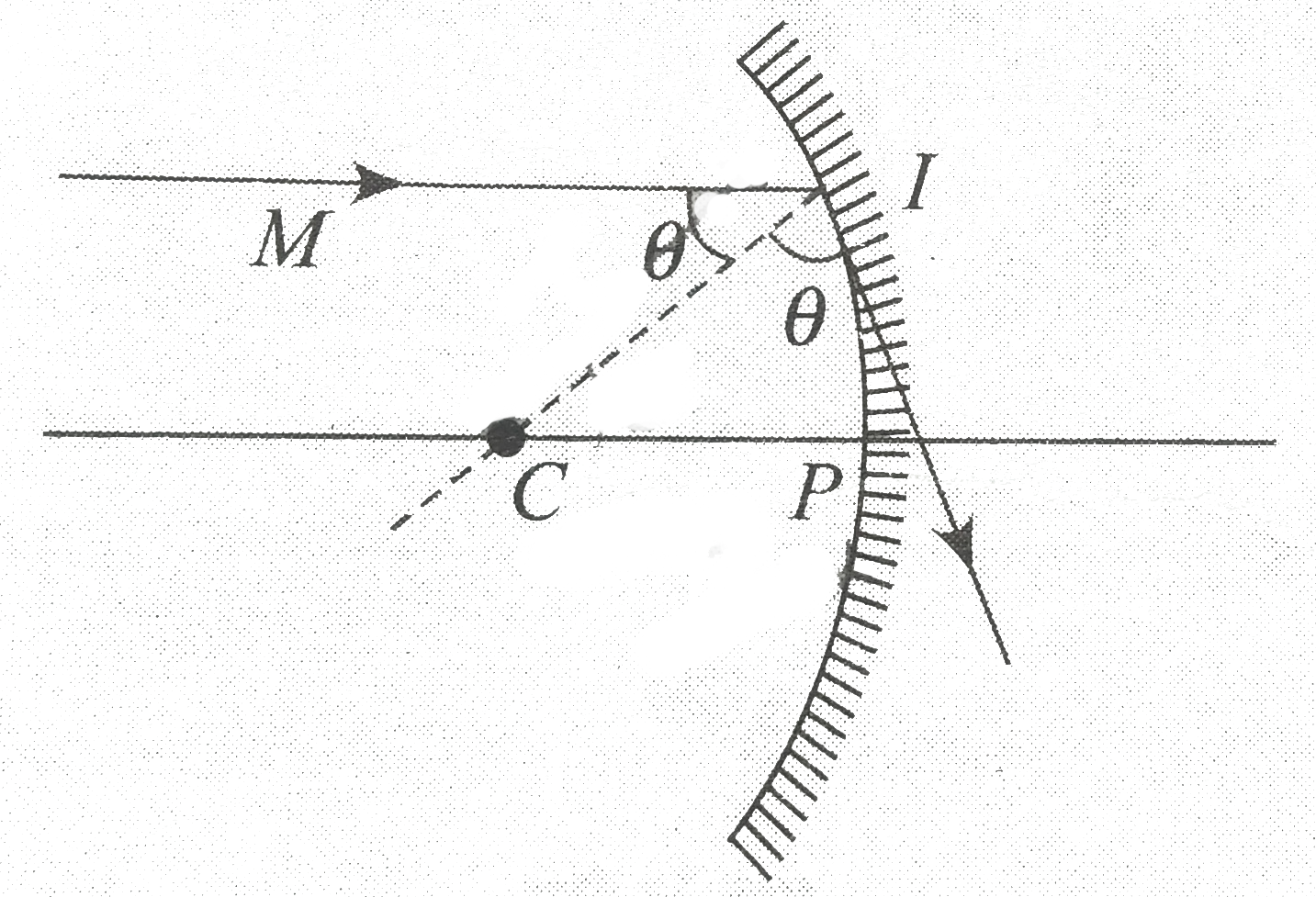
View SolutionFind the distance CQ if incident light ray parallel to principal axis is incident at an angle i. Also, find the distance CQ if `irarr0` .

View SolutionCan a convex mirror form a real image! Explain.
View SolutionAn extended object is placed perpendicular to the principal axis of a concave mirror of radius of curvature 20cm at a distance of 15 cm from the pole. Find the lateral magnification produced.
View SolutionA peson looks into a spherical mirror. The size of image of his face is twice the actual size of his face. If the face is at a distance of 20cm, then find the radius of curvature of the mirror.
View SolutionAn image of a candle on a screen is found to be double its size. When the candle is shifted by a distance of 5cm, then the image becomes triple its size. Find the nature and radius of curvature of the mirror.
View SolutionA point object is placed 60 cm from the pole of a concave mirror of focal length 10 cm on the principal axis.
Find:
a. the position of image.
b. If the object is shifted 1 mm towards the mirror along principal axis, find the shift in image. Explain the result.
View SolutionThe distance between a real object and its image in a convex mirror of focal length 12cm is 32cm. Find the size of image if the object size if 1cm.
View SolutionA plane mirror is placed at a distance of 50 cm from a concave mirror of focal length 16 cm. Where should a short object be placed between the mirrors and facing both the mirrors so that its virtual image in the plane mirror coincides with the real image in concave mirror? What is the ratio of the sizes of the two images?
View SolutionShown in Fig. is a vertically erect object placed on the optic axis at a distance `(5//2)f` from a concave mirror of focal length f. If a plane mirror is placed perpendicular to the optic axis at a distanc `(4//3)f` from the pole, facing concave mirror, find the position and nature of the final image formed.
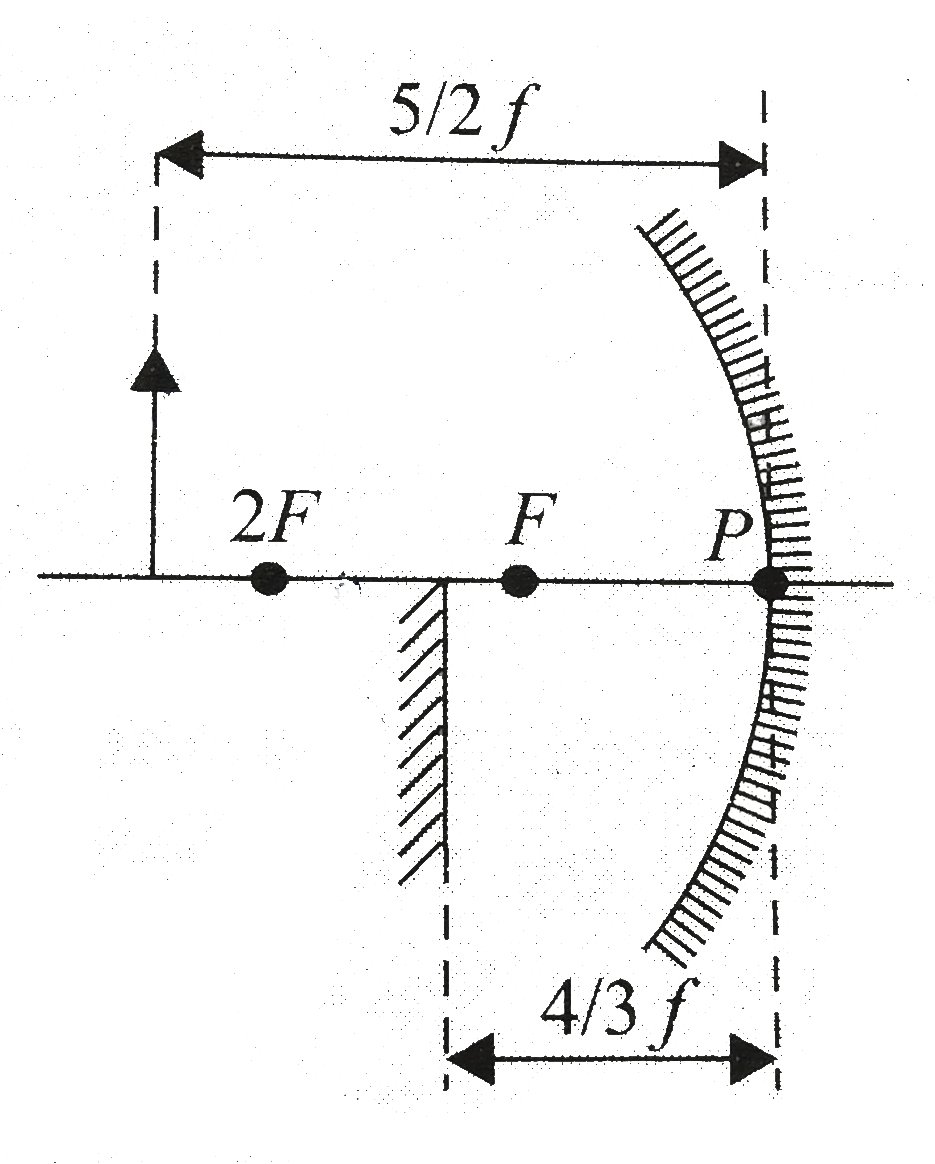
View SolutionTwo concave mirrors are places 40cm apart and are facing each other. A point object lies between them at a distance of 12cm from the mirror of focal length 10cm. The other mirror has a focal length of 15cm. Find the location of final image formed after two reflections - first at the mirror nearer to the object and second at the other mirror.
View SolutionFigure shows a shperical concave mirror of focal length f=5cm with its pole at (0,0) and principal axis along x-axis. There is a point object at (-40cm, 1cm), find the postion of image.

View SolutionA thin rod of length `f//3` is placed along the optical axis of a concave mirror of focal length f such that its image whichis real and elongated just touches the rod. Calculate the magnification.
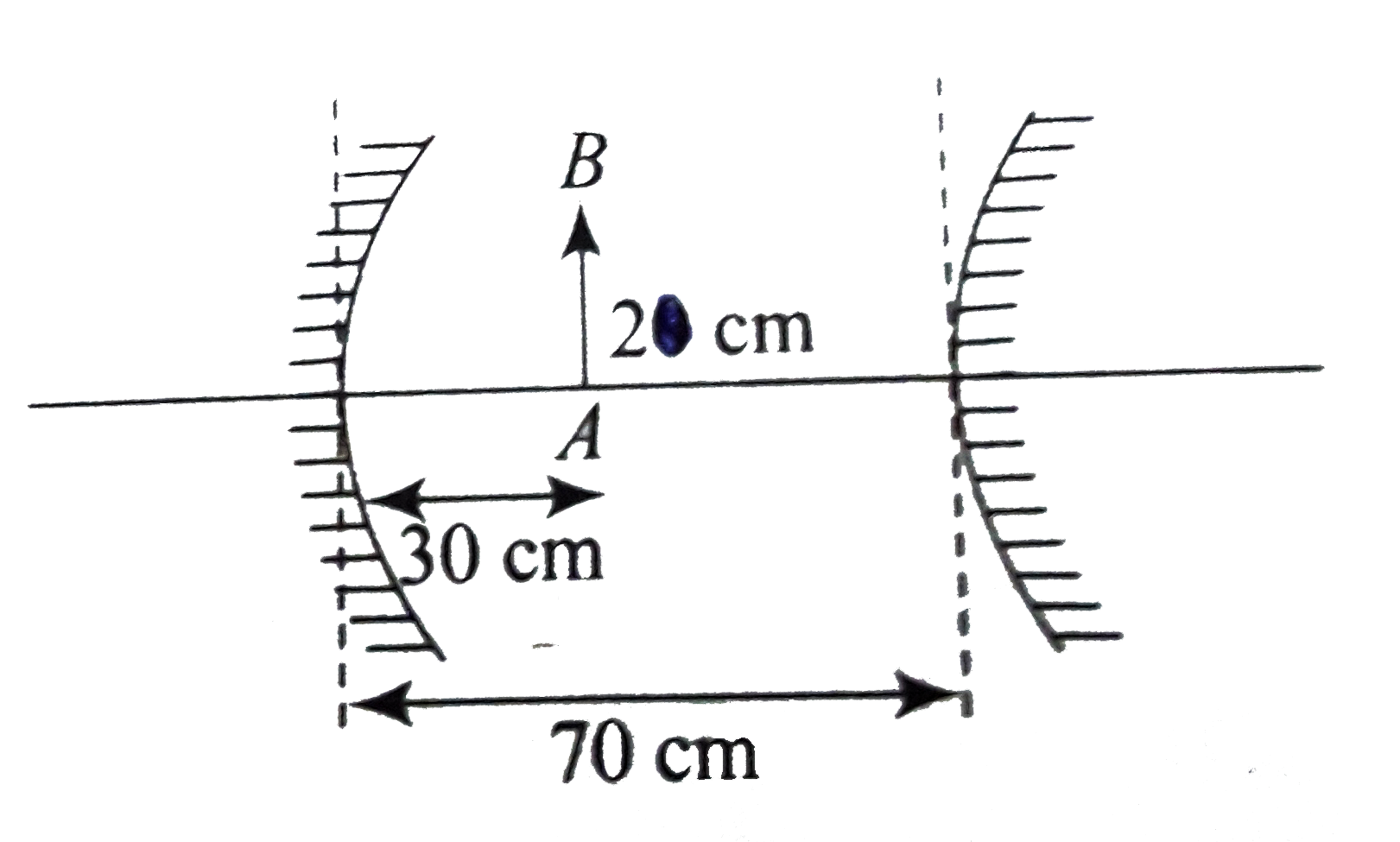
View SolutionA concave mirror and a convex mirror of focal lengths 10cm and 15cm are places at a distance of 70cm. An object AB of height 2cm is places at a distance of 30cm from the concave mirror. First ray is incident on the concave mirror then on the convex mirror. Find size, position, and nature of the image.
View SolutionTwo concave mirrors each of radius of curvature 40cm are placed such that their principal axes are parallel to each other and at a distance of 1cm to each other. Both the mirrors are at a distance of 100cm to each other. Consider first reflection at `M_(1)` and then at `M_(2)` , find the coordinates of the image thus formed. Take location of object as the origin

View SolutionA mirror of radius of curvature 20cm and an object which is placed at a distance of 15cm are both moving with velocities `1ms^(-1)` and `10ms^(-1)` as shown in Fig. Fing the velocity of image at this situation.

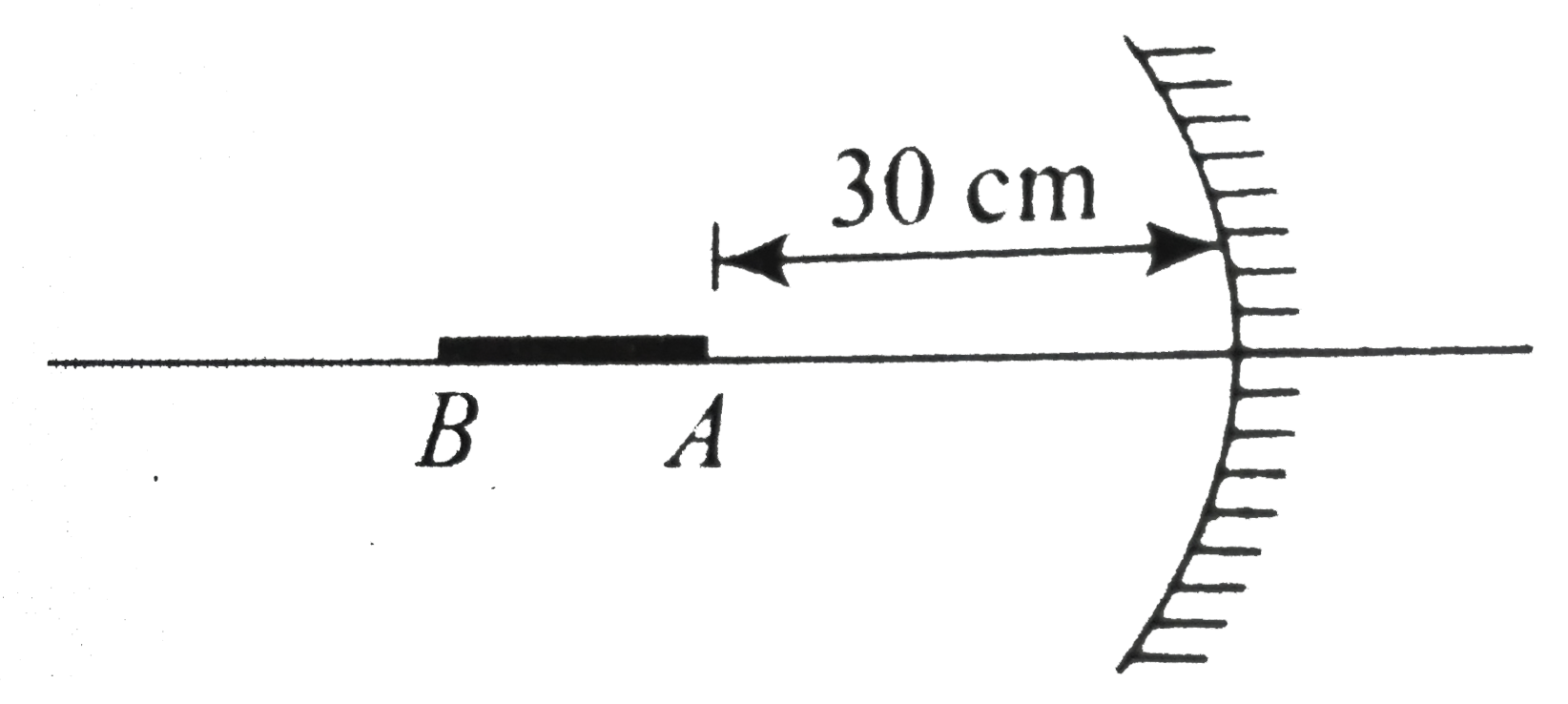
View SolutionObject AB is placed on the axis of a concave mirror of focal length 10cm. End A of the object is at 30cm from the mirror. Find the length of the image
a. if length of object is 5cm.
b. if length of object is 1 mm.
View SolutionDeterming the refractive index of glass with repext to water. Given that `mu=3//2, mu_w=4//3`.
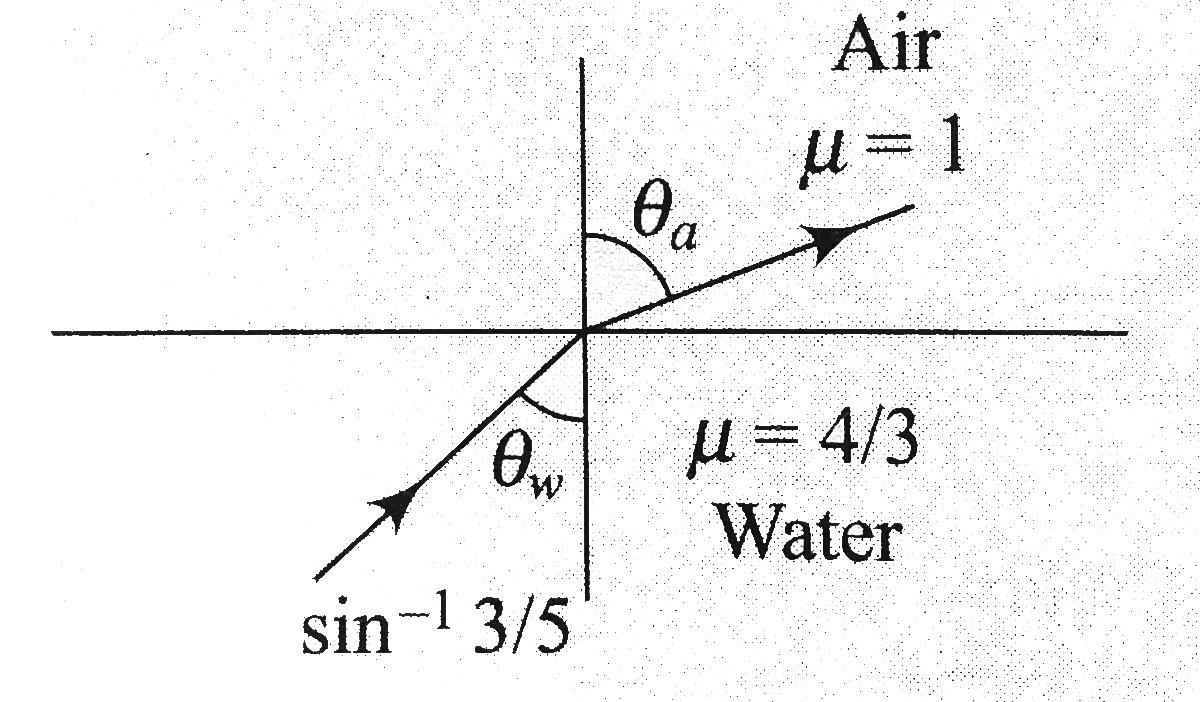
View SolutionFind the angle `theta_a` made by the light ray when it gets refracted from water to air, as shown in Fig .
View SolutionFind the speed of light in medium 'a' if speed of light in medium 'b' is `c//3`, where c =speed of light in vacuum and light refracts from medium 'a' to medium 'b' making `45^(@)` and `60^(@)`, respectively, with the normal.
View SolutionA ray of light is incident on a transparent glass slab of refractive index `sqrt3`. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?
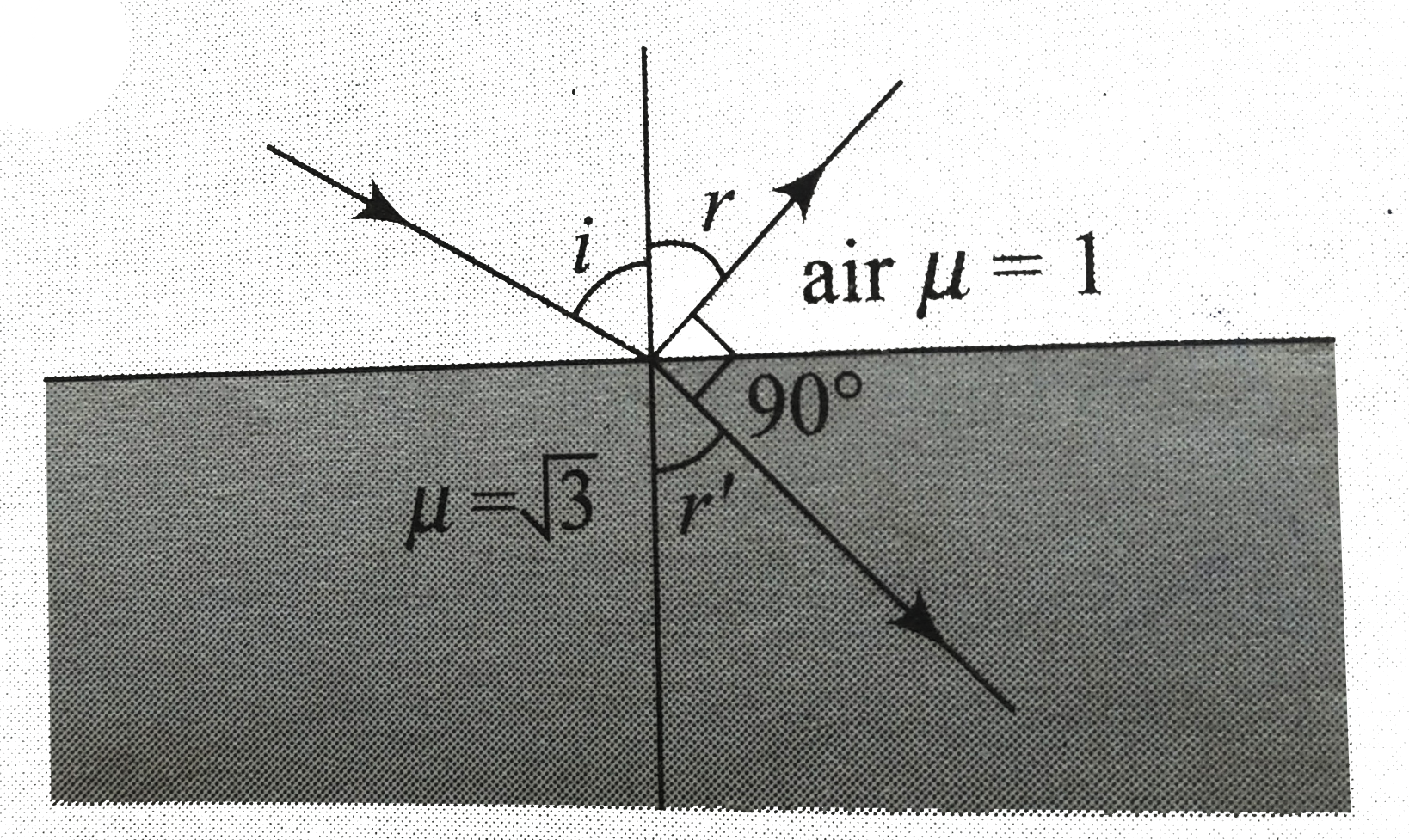
View SolutionA light ray is incident on a glass sphere of reflective index `mu = sqrt3` at an angle of incidence `60^(@)` as shown in Fig. Find the angles r, `r^(')` e and the total deviation after two refractions.
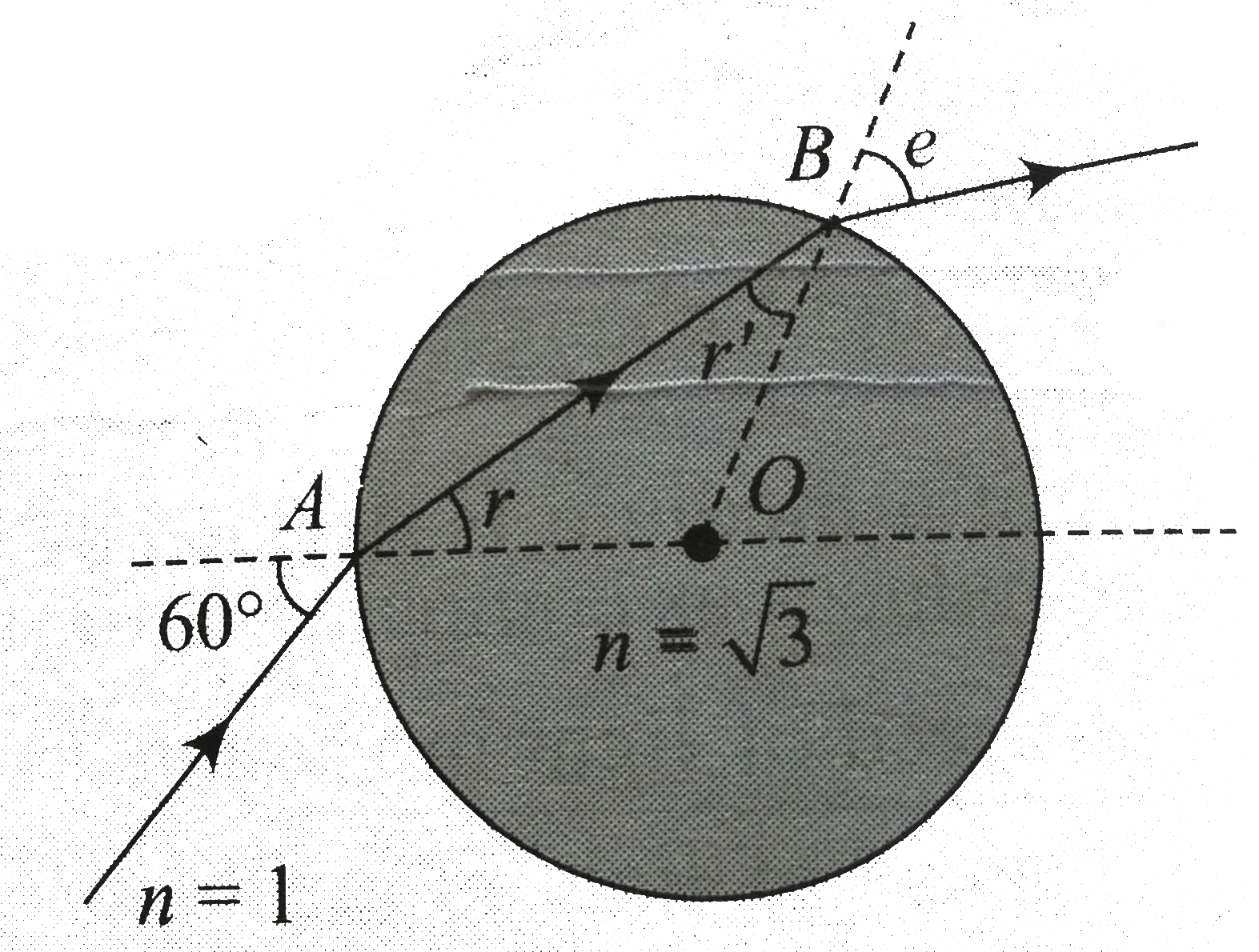
View SolutionA cylindrical vessel, whose diameter and height both are equal to 30 cm, is placed on a horizontal surface and a small particla P is placed in it at a distance of 5.0 cm from the center. An eye is placed at a position such that the edge of the bottom is just visible. The particl P is in the plane of drawing. Up to what minimum height should water be poured in the vessel to make the particle P visible?
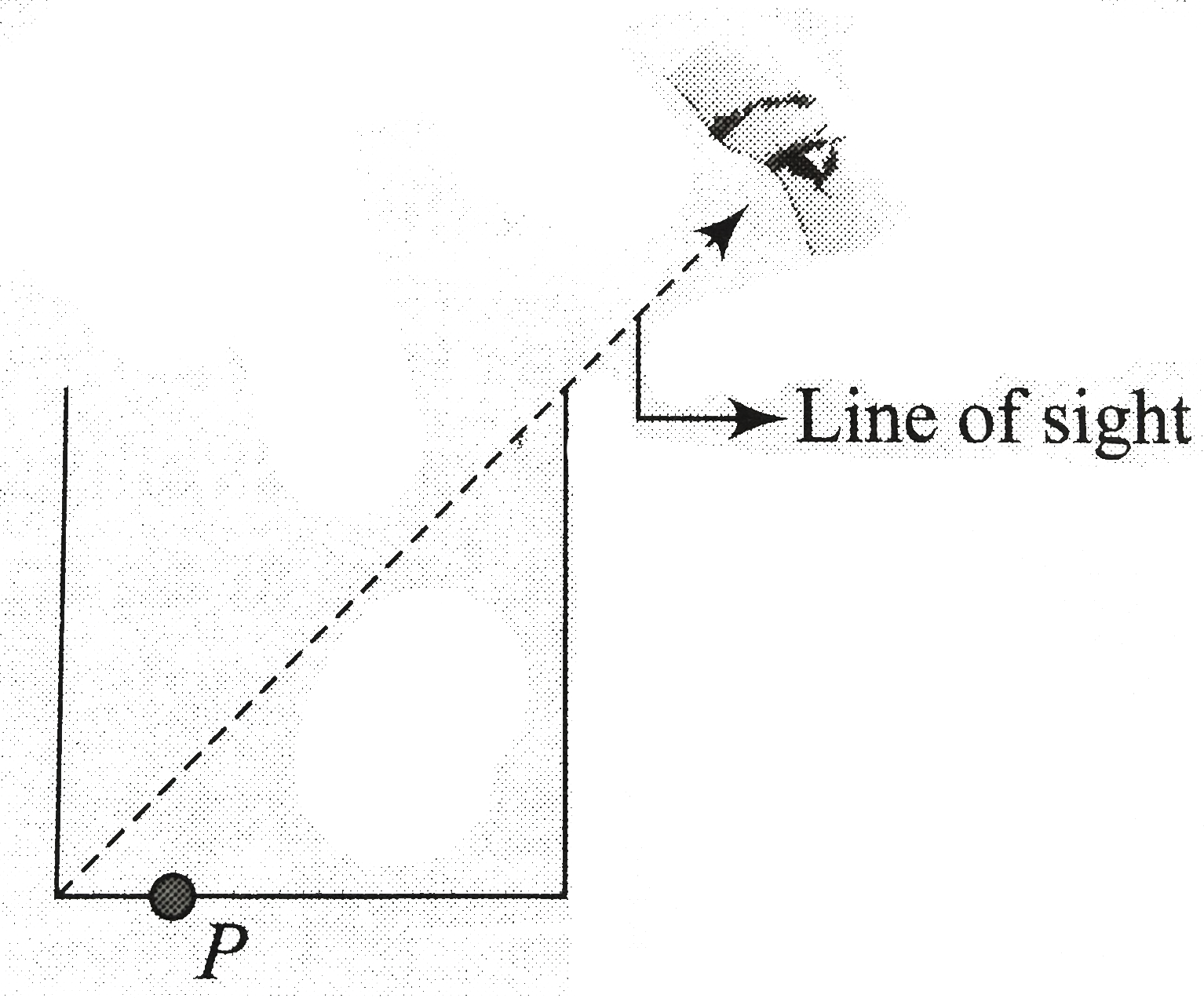
View SolutionLet the x-z plane be the boundary between two transparent media. Medium 1 in `zge0` has a refractive index of `sqrt2` and medium 2 with `zlt0` has a refractive index of `sqrt3`. A ray of light in medium 1 given by the vector `vecA=6sqrt3hati+8sqrt3hatj-10hatk` is incident on the plane of separation. The angle of refraction in medium 2 is:
View SolutionFind the maximum angle that can be made in glass medium `(mu=1.5)` if a light ray is refreacted from glass to vacuum.
View SolutionFind the angle of refraction in a medium `(mu=2)` if light is incident in vacuum, making an angle equal to twice the critical angle.
View SolutionWhat should be the value of angle `theta` so that light entering normally through the surface AC of a prism `(n=3//2)` does not cross the second refracting surface AB?

View SolutionA glass rod having square cross-section is bent into the shape as shown in the figure. The radius of the inner semi-circle is R and width of the rod is d. Find the minimum value of `d//R` so that the light that enters at A will emerge at B. Refractive index of glass is `mu=1.5`

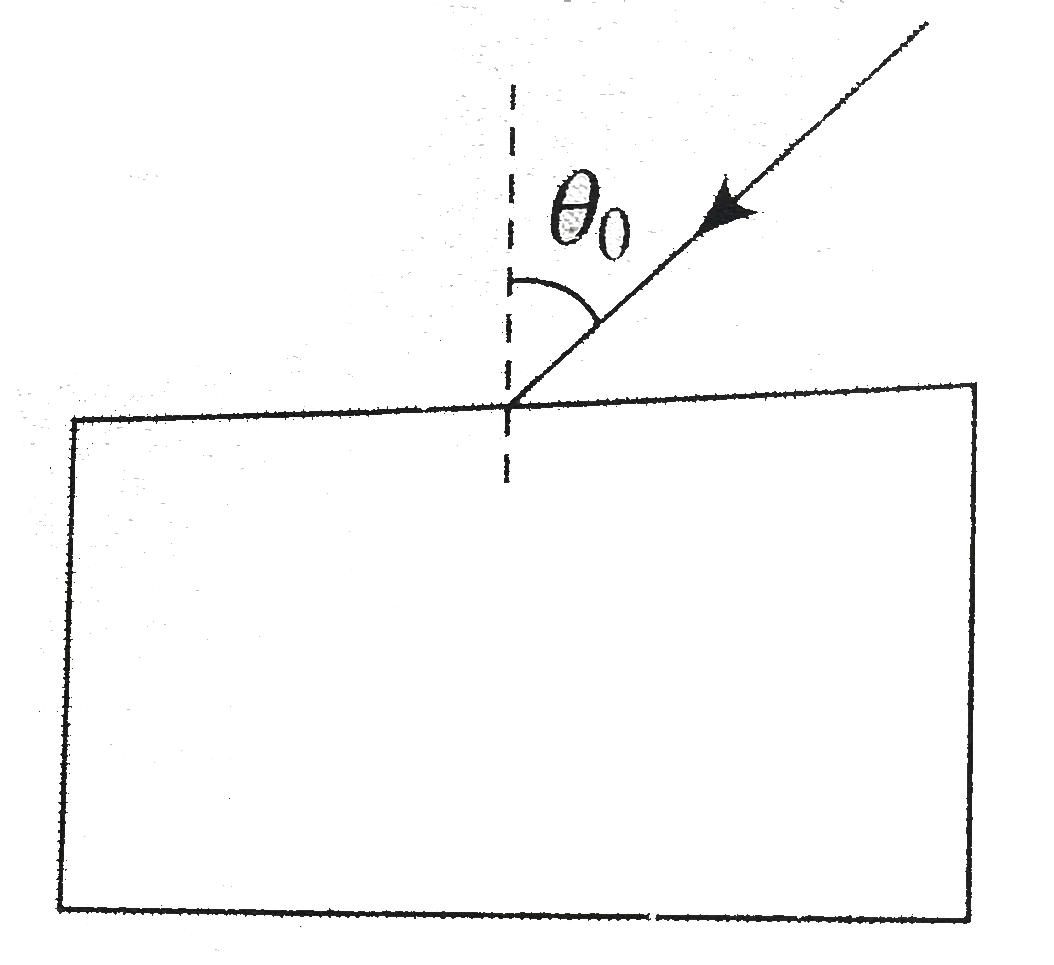
View SolutionA slab of refractive index `mu` is placed in air and light is incident at maximum angle `theta_0` from vertical. Find minimum value of `mu` for which total internal reflection takes place at the vertical surface.
View SolutionA rectangular slab ABCD, of refractive index `n_1` , is immersed in water of refractive index `n_2(n_1 lt n_2)`. A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence `alpha_(max)`, such that the ray comes out only from the other surface CD.
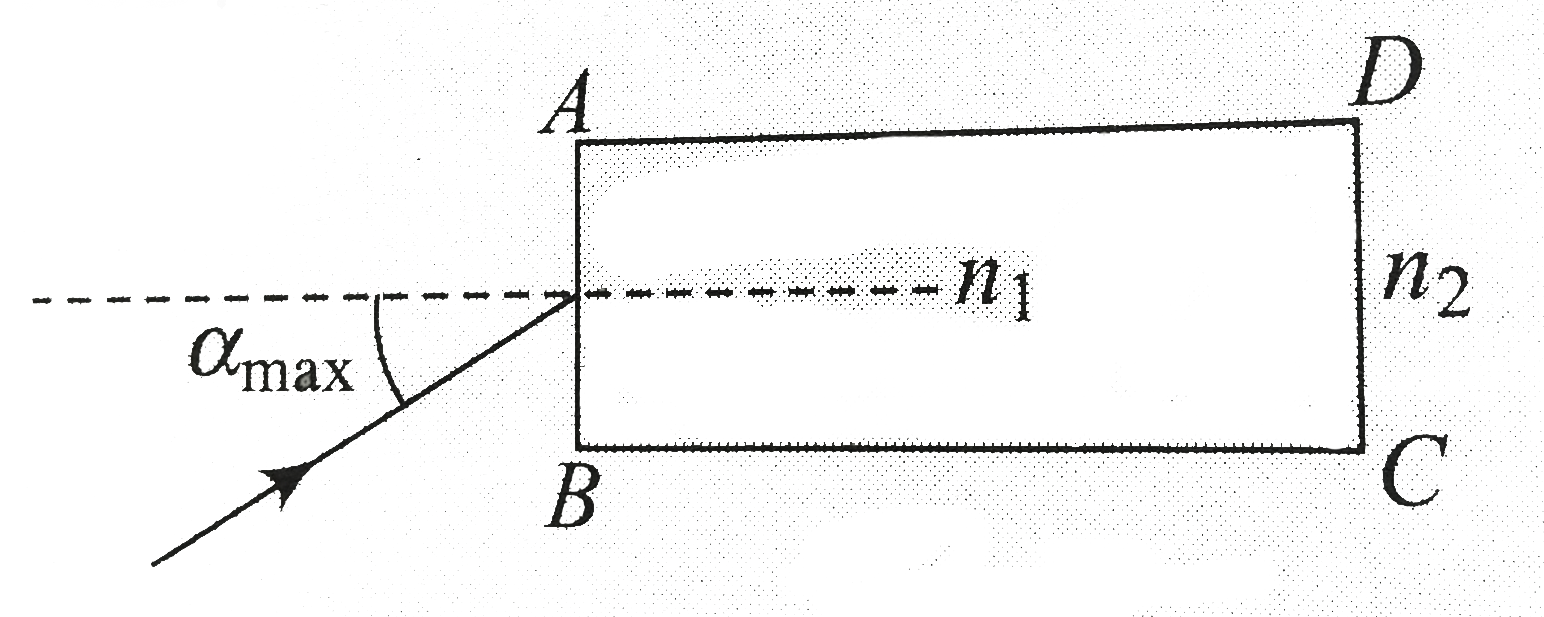
View SolutionA point source of light is placed at distance h below the surface of a large and deep lake. What fraction of light will escape through the surface of water?
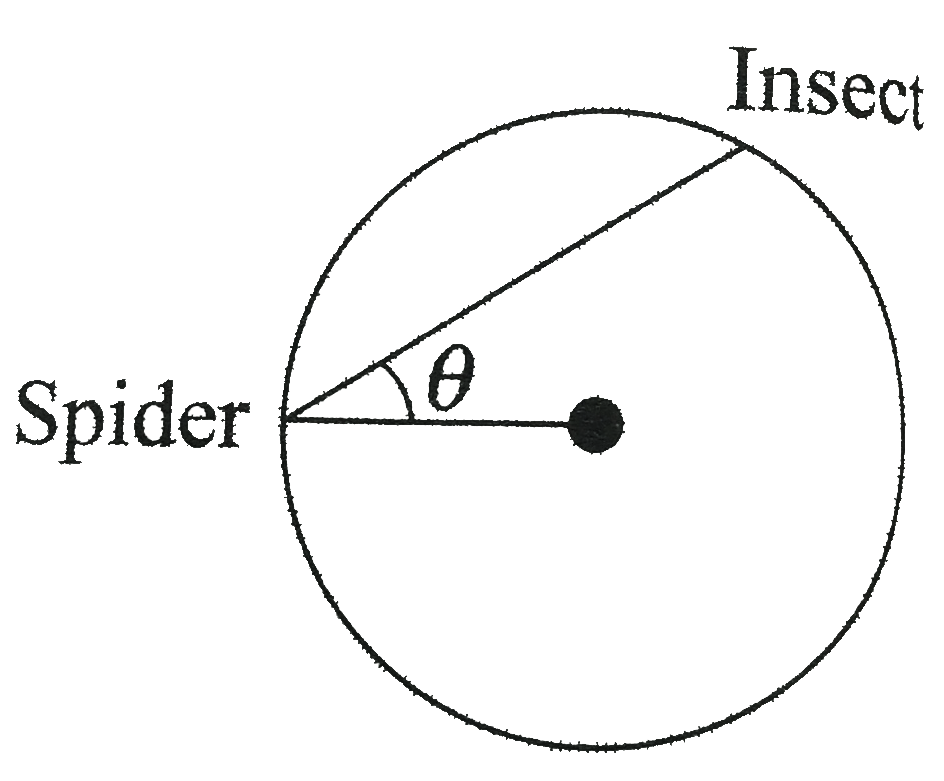
View SolutionA spider is on the surface of a glass sphere with a refractive inndex of `1.5` . An insect crawls on the other side of the sphere as shown in Fig. For what maximum value of `theta` will the spider be able to still see the insect. Assume the spiders eye is in air.
View SolutionA monochromatic light is incident on the plane interface AB between two media of refractive indices `mu_(1)` and `(mu_(2)gtmu_(1))` at an angle of incidence `theta` as shown in Fig.
The angle `theta` is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index `mu_(3)` is introduced on the interface (as shown in the figure), show that for any value of `mu_(3)` all light will ultimately be reflected back into medium II.

View SolutionAn object lies 100 cm inside water `(mu=4//3)`. It is viewed from air nearly normally. Find the apparent depth of the object.
View SolutionSee Fig. and answer the following question.
a. Find apparent height of the bird.
b. Find apparent depth of the fish.
c. At what distance will the bird appear to the fish ?
d. At what distance will the fish appear to the bird?

View SolutionConsider the situation in Fig. The bottom of the pot is a reflecting plane mirror, S is a small fish, and T is a human eye. Refractive index of water is `mu`.
a. At what distance(s) from itself will the fish see the image(s) of the eye?
b. At what distance(s) from itself will the eye see the image(s) of the fish?

View SolutionConsider the situation skteched. A fish lies 40 cm under the surface of water `(mu_(water)=4//3)`, 80 cm above a concave spherical mirro whose radius of curvature is 120cm. An observer looking down from above in the air `(mu_(air)=1)` sees two images of fish. Find distance (in meters) between these two images.

View SolutionA fish in an aquarium approaches the left wall at a rate of `3ms^(-1)` observes a fly approaching it at `8ms^(-1)`. If the refractive index of water is `(4//3)`, find the actual velocity of the fly.

View SolutionFind the lateral shift of a light ray while it passws through a parallel glass slab of thickness 10 cm places in air. The angle of incidence in air is `60^(@)` and the angle of refraction in glass is `45^(@)`.
View SolutionIn Fig. , find the apparent depth of the object seen below surface AB.

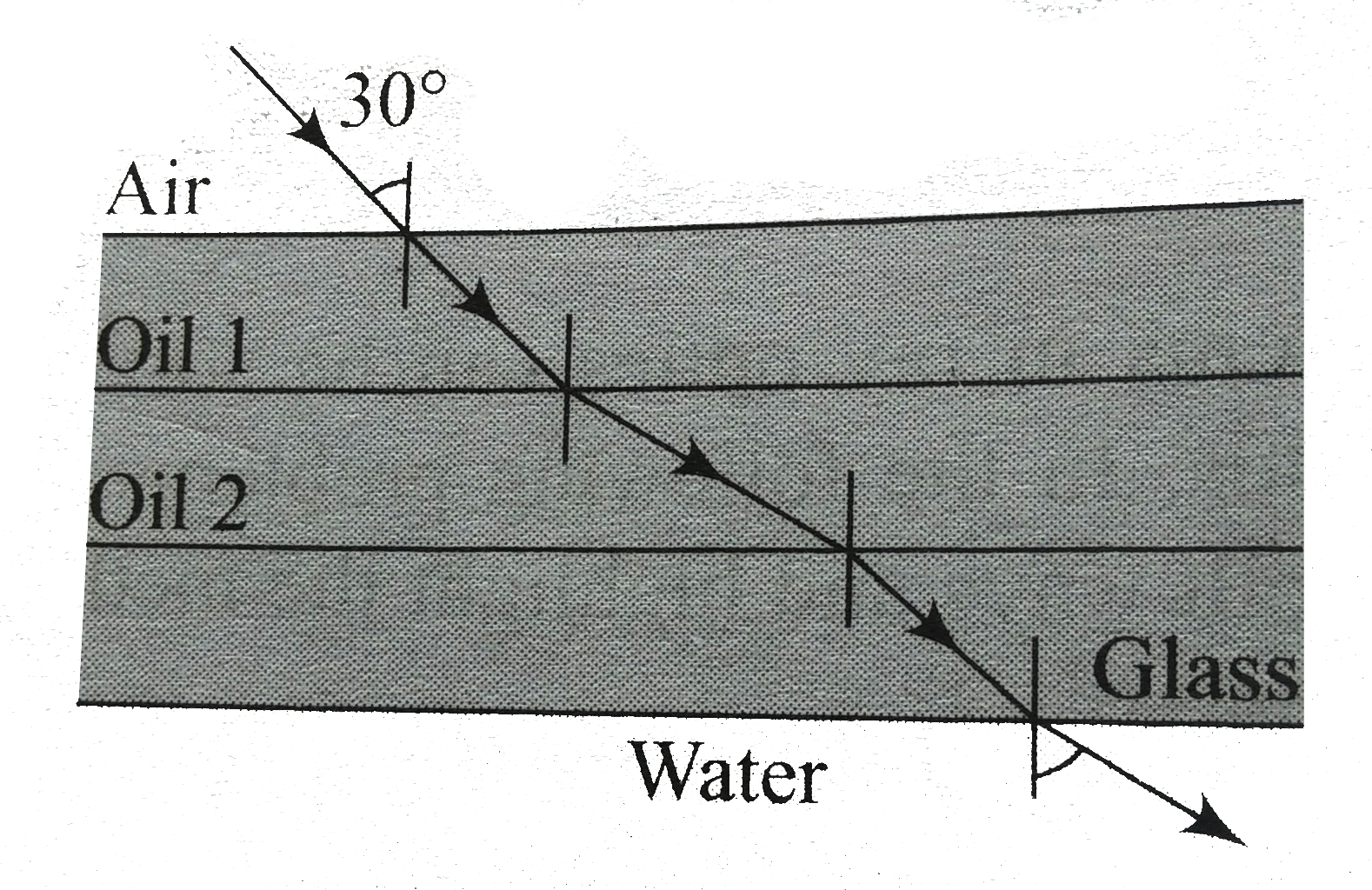
View SolutionLight is incident from air on an oil layer at an incident angle of `30^(@)`. After moving through the oil 1, oil 2, and glass it enters water. If the refraction index of glass and water are `1.5` and `1.3`, respectively. Find the angle which the ray makes with the normal in water.
View SolutionA layer of oil 3 cm thick is floating on a layer of coloured water 5 cm thick. Refractive index of coloured water is `5//3` and the apparent depth of the two liquids appears to be `36//7`cm. Find the refractive index of oil.
View SolutionIn Fig., determine the apparent shift in the position of the coin. Also, find the effective refractive index of the combinatino of the glass and water slab.

View SolutionA small object is placed 20 cm in front of a block of glass 10 cm thick and its farther side silvered. The image is formed 22 cm behind the silvered face. Find the refractive index of glass.
View SolutionA `20cm` thick glass slab of refractive index `1.5` is kept in front of a plane mirror. Find the position of the image (relative to mirror) as seen by an observer through the glass slab when a point object is kept in air at a distance of `40 cm` from the mirror.
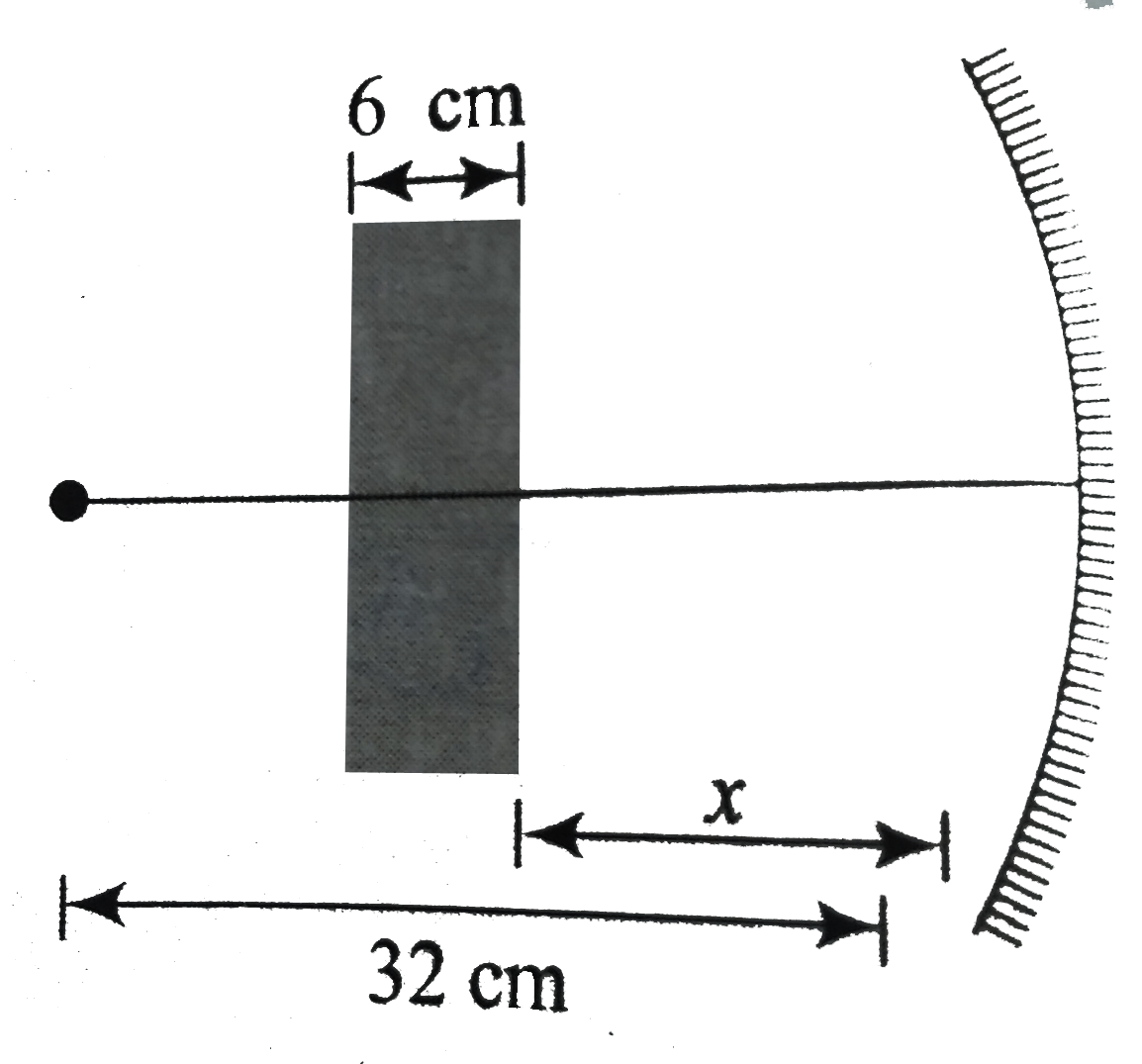
View SolutionA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index `mu=3//2` and thickness 6cm is inserted between the object and mirror.
Find the position of final image when the distance x shown in Fig... is, (a) 5cm and (b) 20 cm.
View SolutionA vessel having perfectly reflecting plane botton is filled with water `(mu=4//3)` to depth d. A point source of light is placed at a height h above the surface of water. Find the distance of final image from water surface.
View SolutionA concave mirror of focal length `20cm` is placed inside water with its shining surface upwards and principal axis vertical as shown in Fig. Rays are incident parallel to the principal, axis of concave mirror. Find the position of final image.

View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by `mu=sqrt((1+y)` . If the thickness of the slab is `d=2m`, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionDue to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as `n=n_(0)``sqrt(1+ay)`, where `n_(0)` is the index of refraction at the surface and `a=2.0xx10^(-6)m^(-1)` . A person of height `h=2.0 m` stands on a level surface. Beyond what distance will he not see the runway?

View SolutionWhat should be the minimum value of refractive index of a prism, refracting angle A, so that there is no emergent ray irrespective of the angle of incidence?

View SolutionAn isosceles prism has one of the refracting surfaces silvered. A ray of light is incident normally on the refracting face AB. After two reflections, the ray emerges from the base of the prism perpendicular to it. Find the angle of the prism.
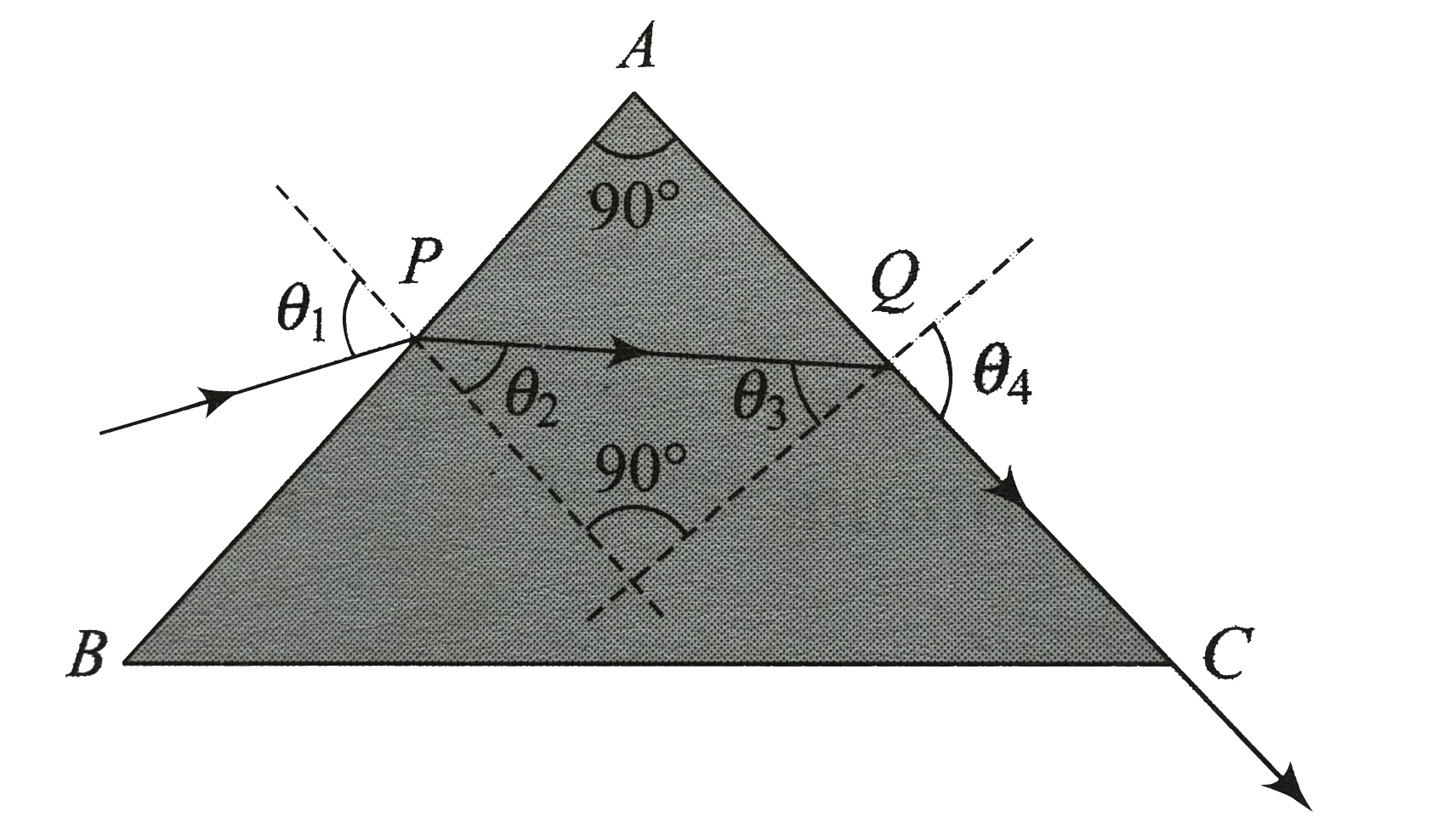
View SolutionFigure.. Shows a triangular prism of refracting angle `90^(@)` . A ray of light incident at face AB at an angle `theta _(1)`, refracts at point Q with an angle of refraction `90^(@)`.
a. What is the regractive index of the prism in terms of `theta_(1)`?
b. What is the maximum value that the refractive inde can have?
c. What happens to the light at Q if the incident angle at Q is (i) increased slightly, and (ii) decrease slightly?
View SolutionA prism has refracting angle equal to `pi//2`. It is given that `gamma` is the angle of minimum deviation and `beta` is the deviation of the ray entering at grazing incidence. Prove that `singamma=sin^(2)beta` .
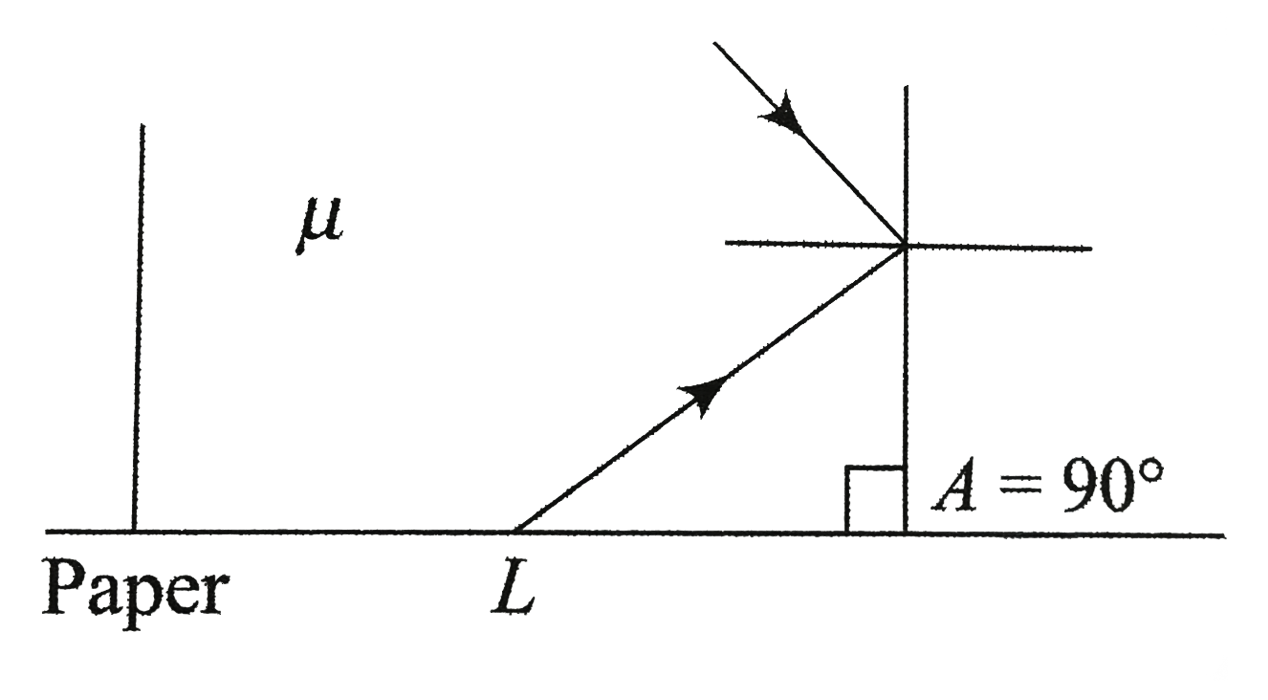
View SolutionA rectangulat block of refractive index `mu` is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of `mu` so that the letter L on the page is not visible from any of the vertical sides.
View SolutionThe cross section of a glass prism has the form of an isosceles triangle. One of th erefracting faces is silvered. A ray of light falling normally on the other refracting face, being reflected twice, emerges through the base of the prism perpendicular to it. Find the angles of the prism.
View SolutionFor a prism, `A=60^(@), n=sqrt(7//3)` . Find the minimum possible angle of incidence, so that the light ray is refracted from the second surface. Also, find `delta_(max)`.
View SolutionA thin biprism (see Fig..) of obtuse angle `alpha=178^(@)` is places at a distance `l=20cm` from a slit. How many images are formed and what is the separation between them? Refrative index of the material `mu=1.6` .
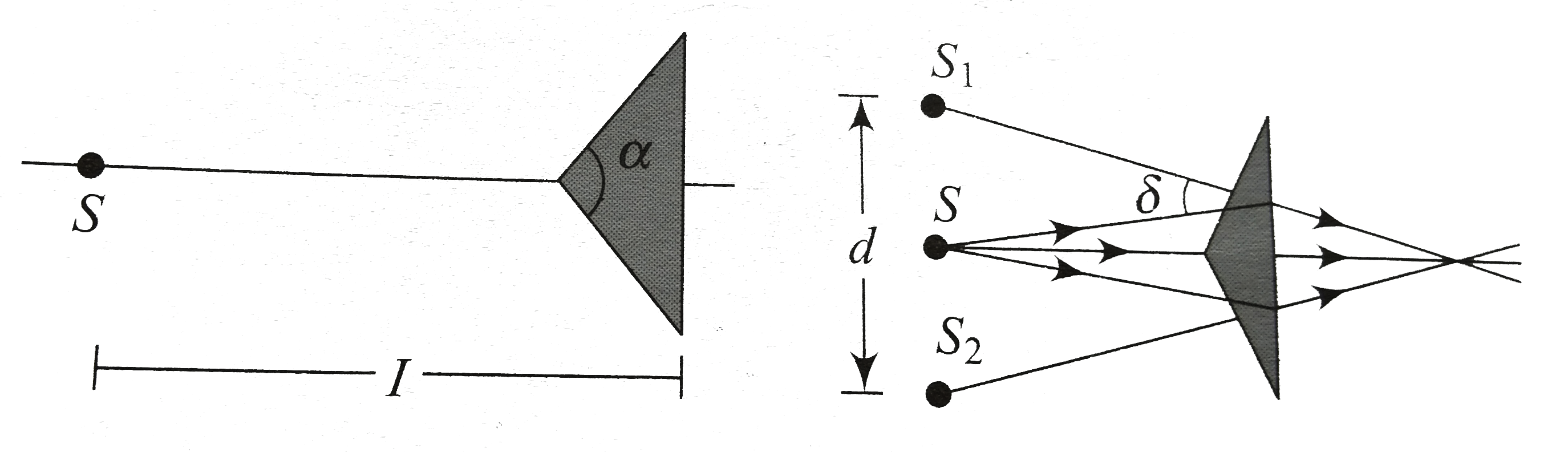
View SolutionA thin prism of angle `A=6^(@)` produces a deviation `d=3^(@)`. Find the refractive index of the material of prism.


View SolutionCalculate the dispersive power for crown glass from the given data
`mu_(v)=1.523` and `mu_(r)=1.5145`.
View SolutionFind the dispersion produced by a thin prism of `18^(@)` having refractive index for red ligh `=1.56` and for violet light `=1.68`.
View SolutionTwo thin prisms are combined to form an achromatic combination. For prism I, `A=4^(@),mu_(R)=1.35, mu_(Y)=1.40,mu_(v)=1.42` For prism II, `mu_(R)^(')=1.7, mu_(Y)^(')=1.8 and mu_(V)^(')=1.9` . Find the prism angle of prism II and the net mean deviation.
View SolutionA crown glass prism of angle `5^(@)` is to be combined with a flint prism in such a way that the mean ray passes undeviated. Find (a) the angle of the flint glass prism needed and (b) the angular dispersion produced by the combinatino when white light goes through it. Refractive indices for red, yellow, and violet light are 1.541, 1.517 and 1.523, repectively, for crown flass and 1.613, 1.620 and 1.632 for flint glass.
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View SolutionShown in the Fig. is a spherical surface of radius of curvature R and R.I. `(=n)1.5`. Find the distance of the silvering of the plane surface so as to form an image at the pole due to a very far object.
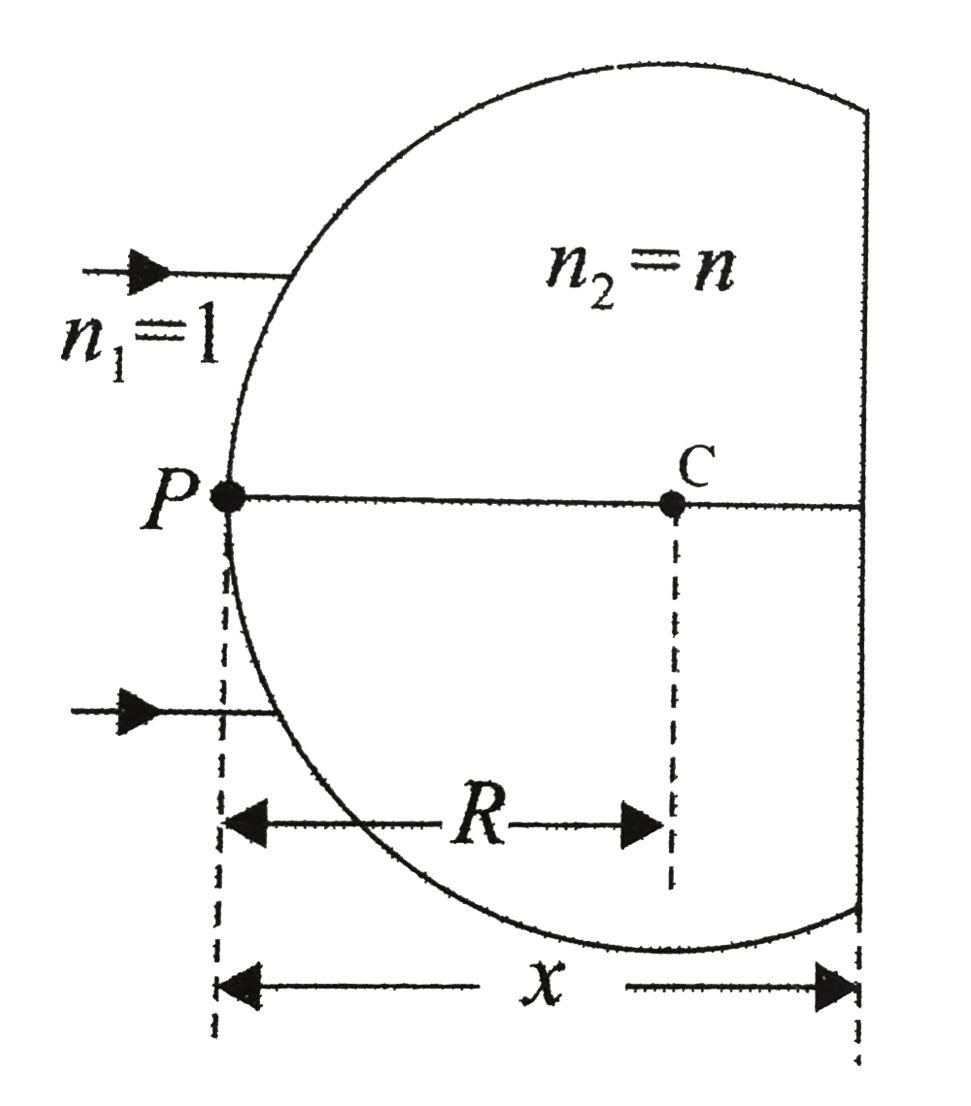
View SolutionA ring of radius 1cm is placed 1m in front of a spherical glass ball of radius 25cm with refractive index 1.50. Determing the positiion of the final image of the ring and its magnification.
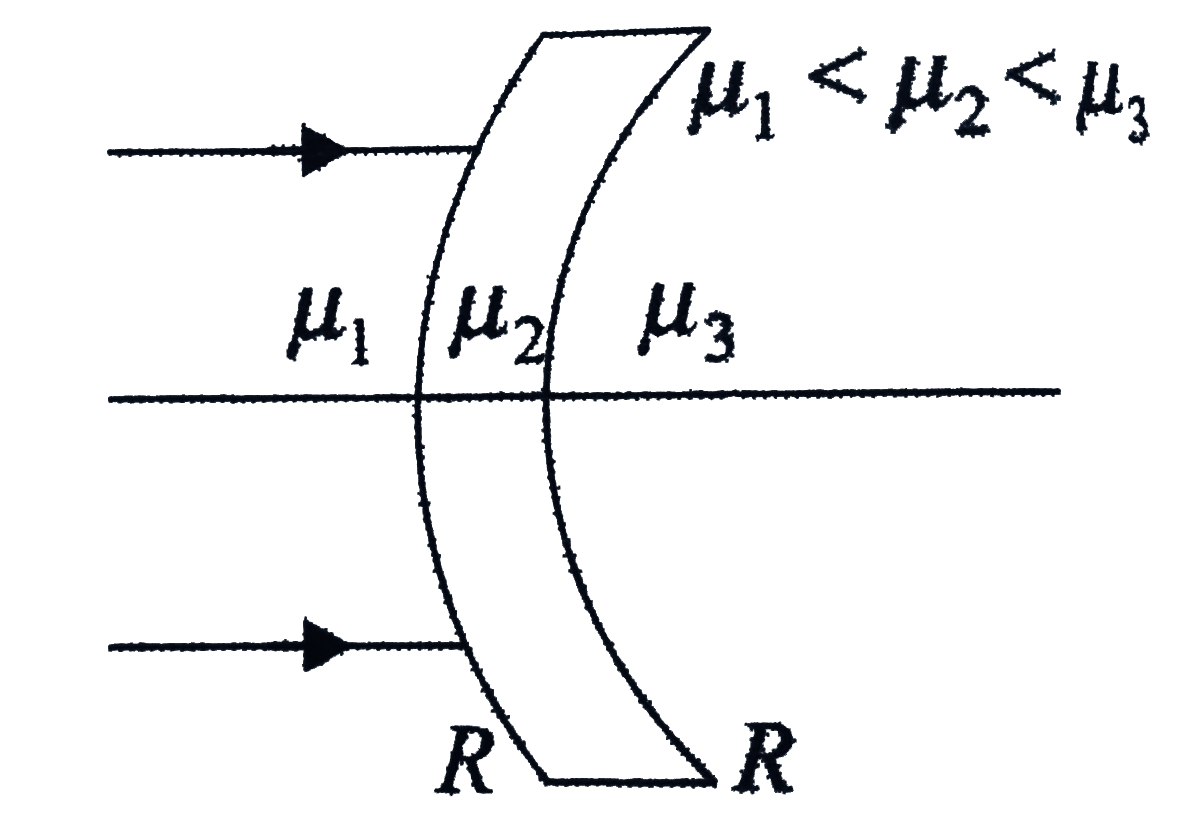
View SolutionA glass sphere of radius 2R, refractive index n has a spherical cavity of radius R, concentric with it. A black spot on the inner surface of the hollow sphere is viewed from the left as well as right. Obtain the shift in position of the object.
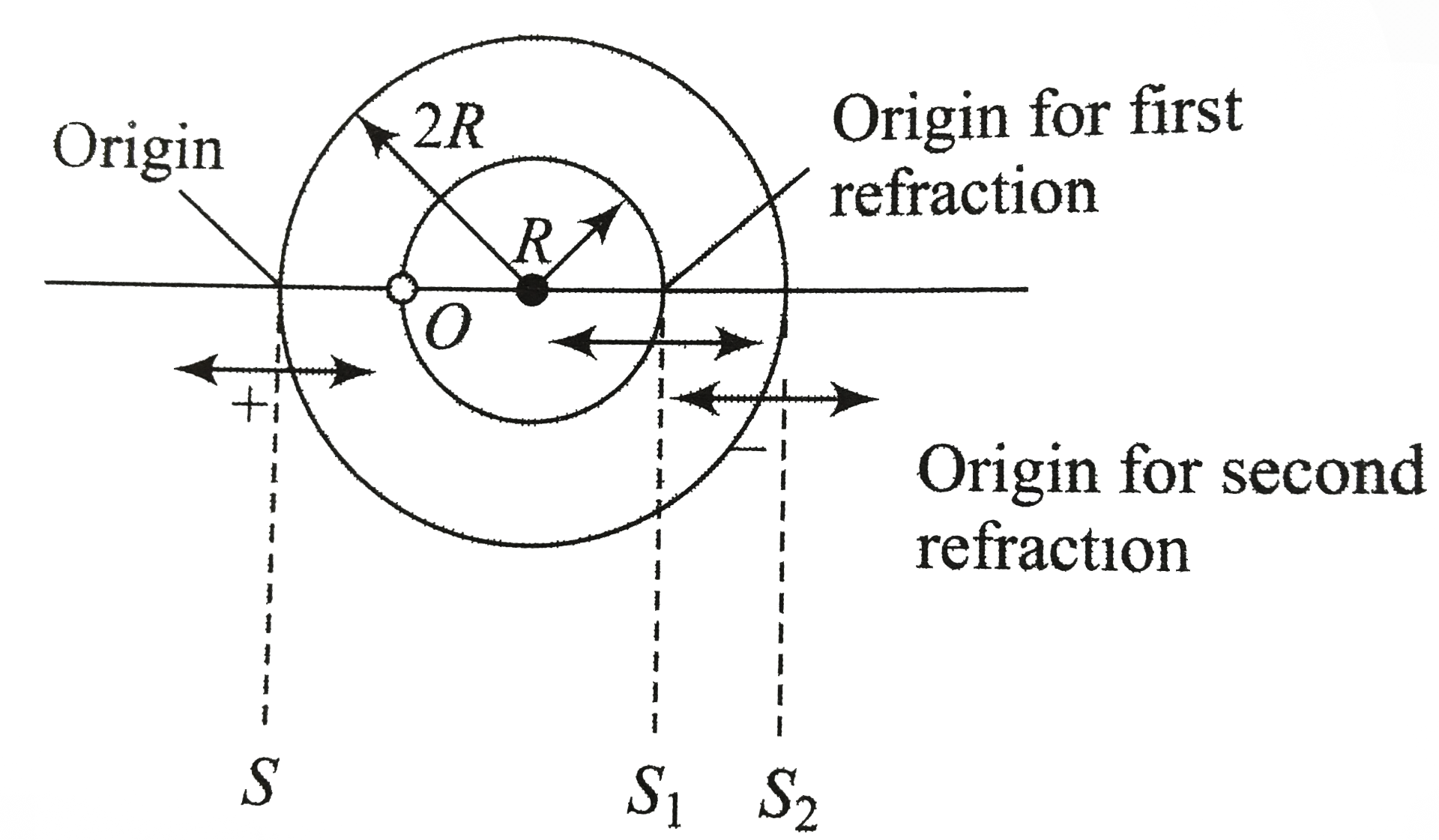
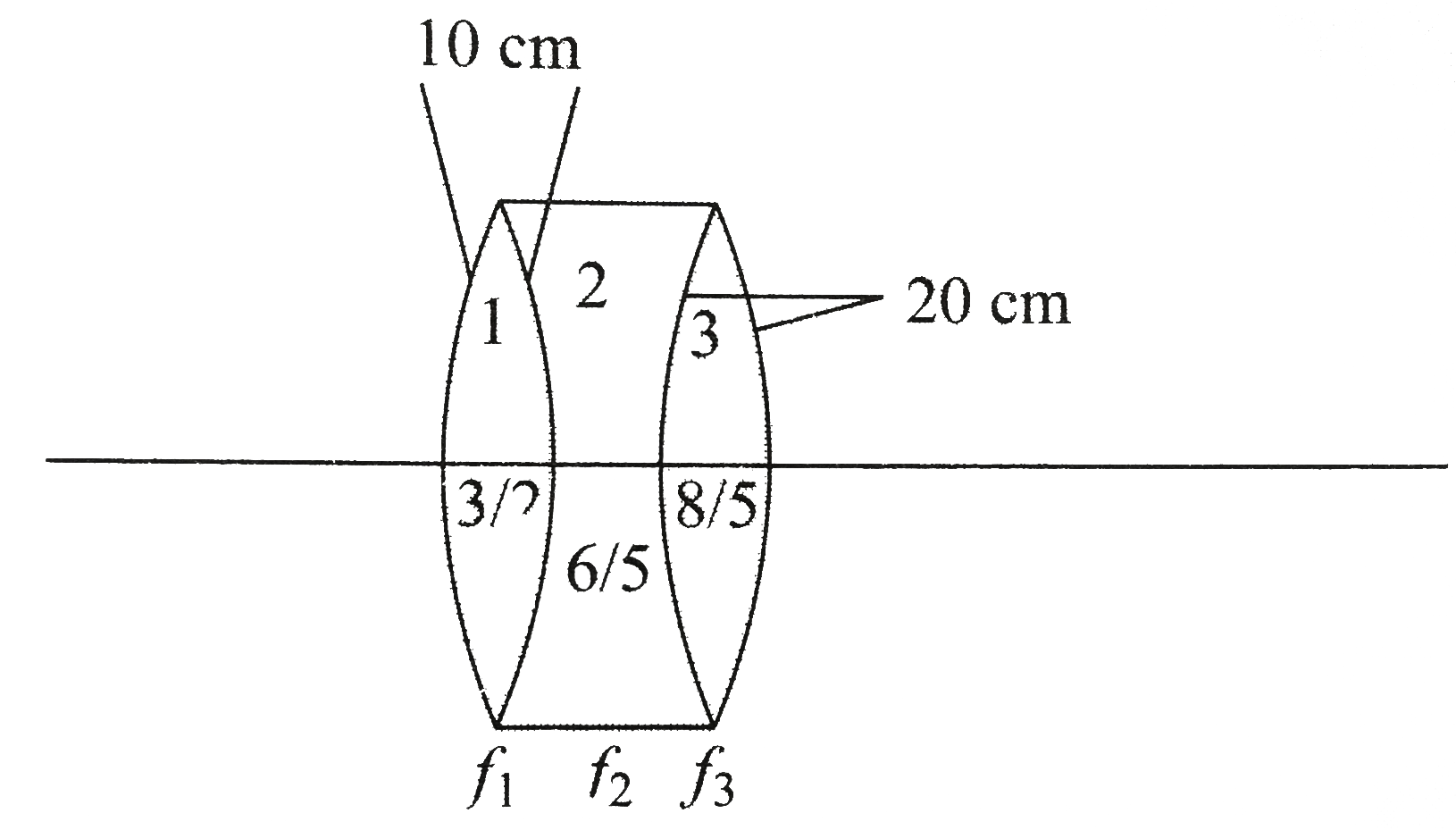
View SolutionFind the focal length of the lens shown in the Fig..
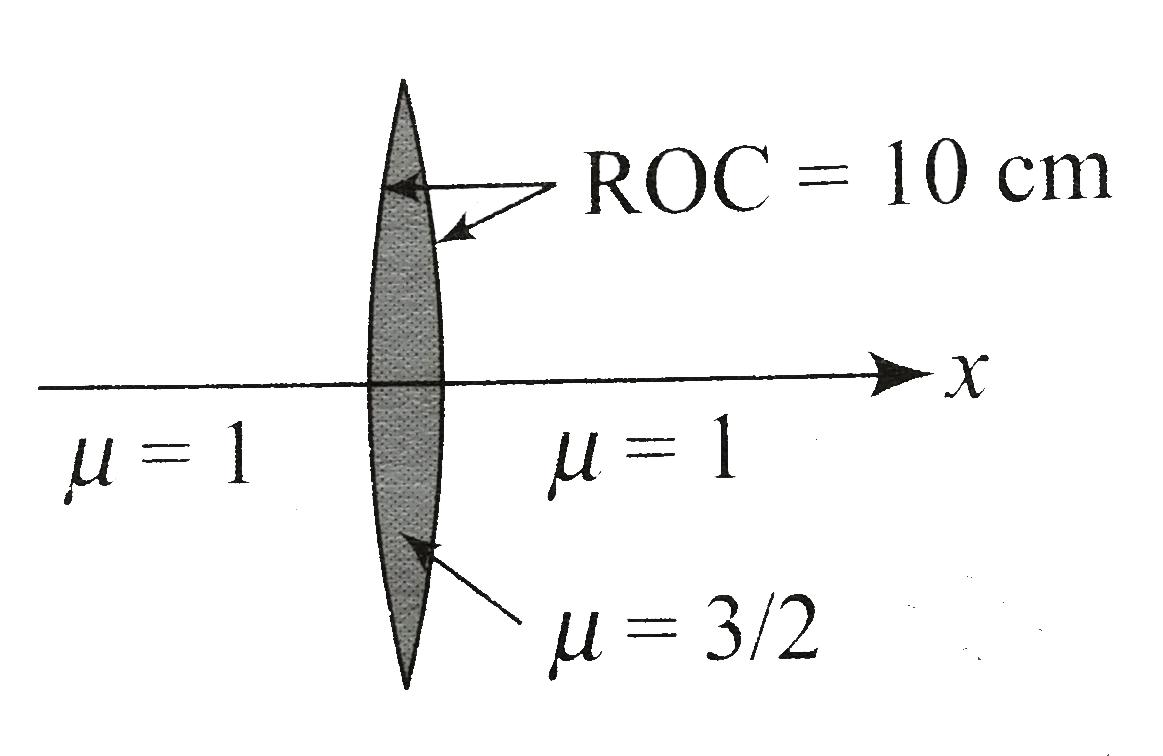
View SolutionFind the focal length of the lens shown in Fig.
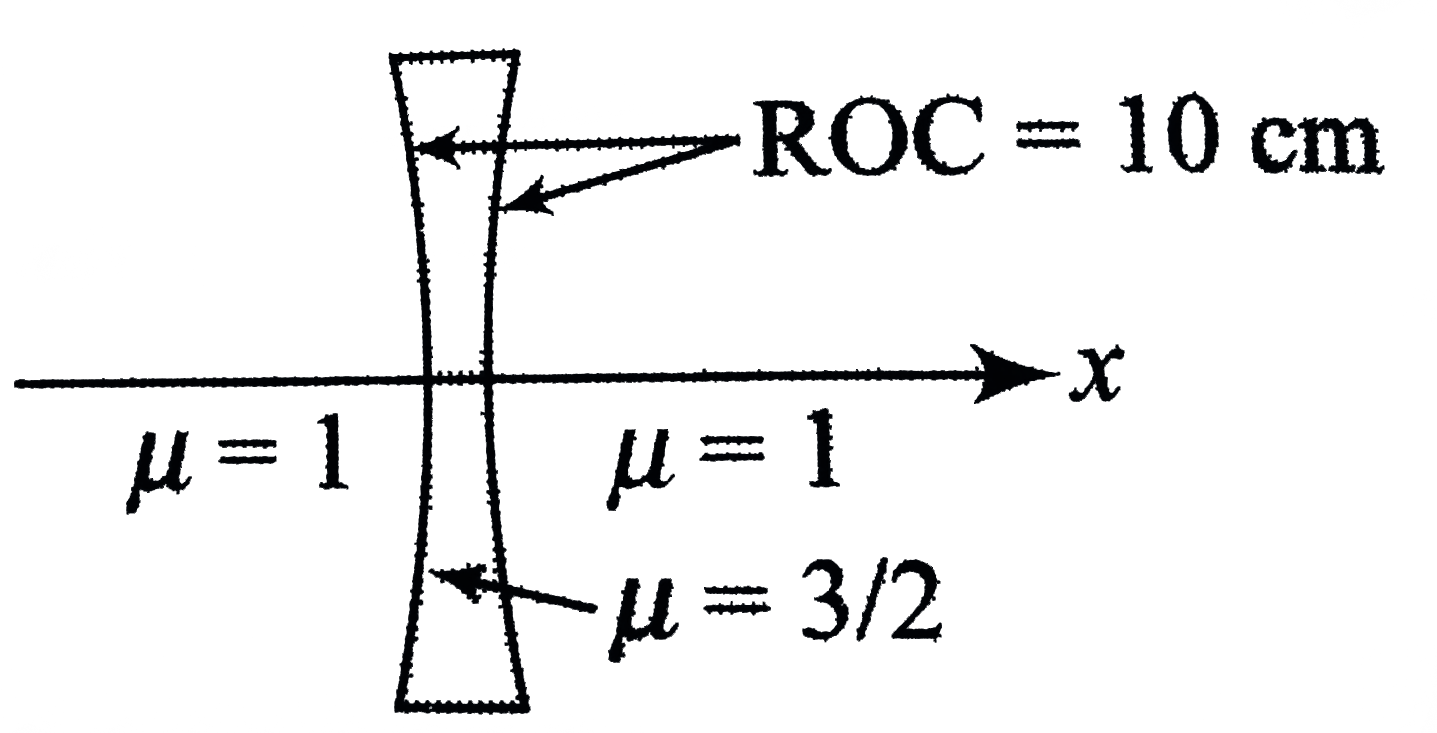
View SolutionA point object is places on the principal axis of a thin lens with parallel curved boundaries, i.e., having same radii of curvature. Discuss about the position of the image formed.
View SolutionFocal length of a thin lens in air is 10cm. Now, medium on one side of the lens is replaced by a medium of refractive inidex `mu=2`. The radius of curvature of the surface of lens, in contact with the medium, is 20cm. Find the new focal length.
View SolutionA glass or glycerin convex lens of refractive index `3//2` has got a focal length equal to 50 cm. Find the focal length of the lens, if it is immersed in ethyl alcohol of refractive index 1.36.
View SolutionThere are two spherical surfaces of radii `R_(1)=30cm` and `R_(2)=60cm`. In how many ways these surfaces may be arranged to get different lenses. If all the lenses are made of glass `(mu=1.5)` , find the focal length of each lens.

View SolutionA thin lens made of a material of refractive index `mu_(0)` has a focal length `f_(0)` in air. Find the focal length of this lens if it is immersed in a liquid of refractive index `mu`.
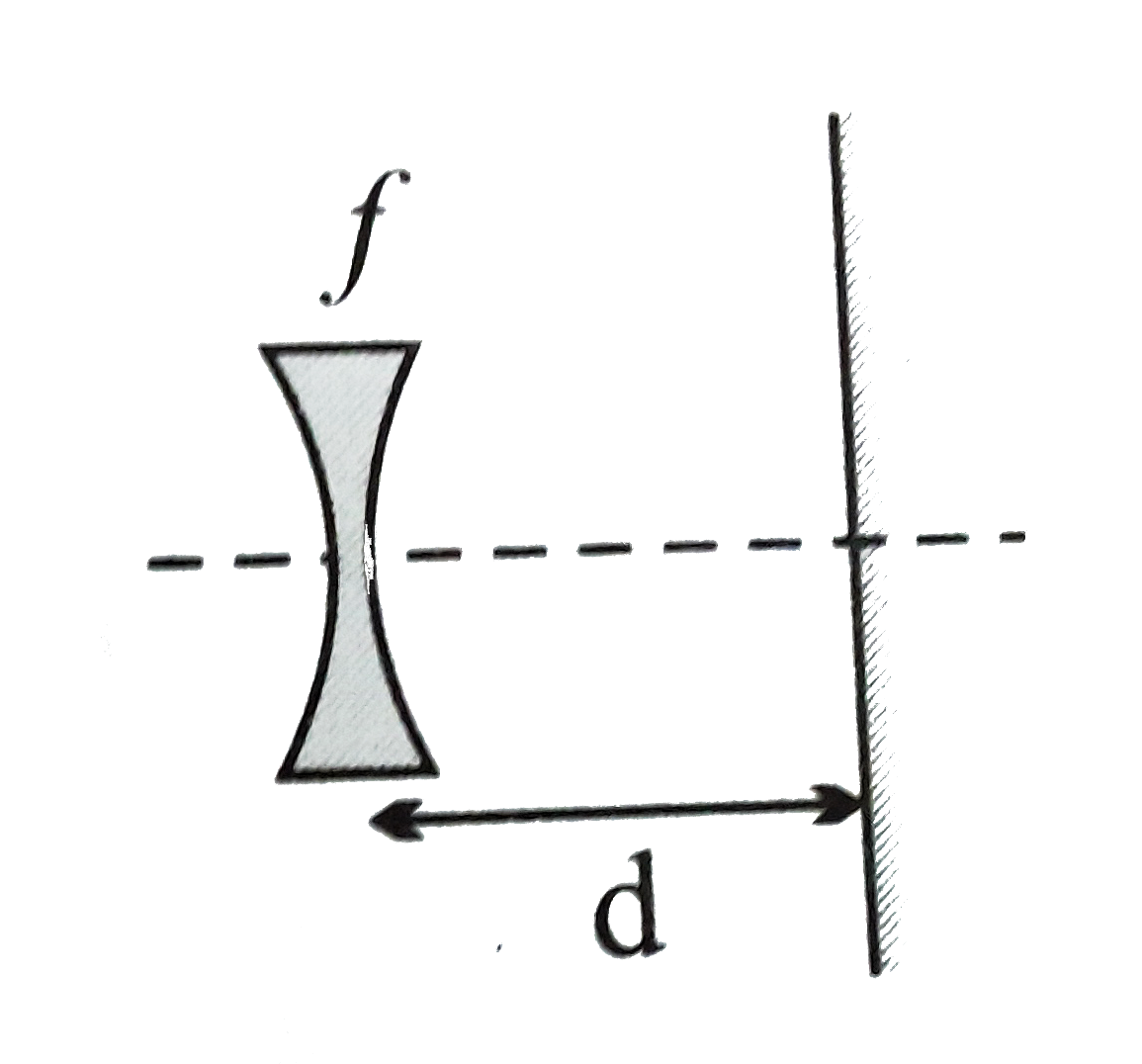
View SolutionA diverging lens of focal length 10cm is placed 10cm away in front of a plane mirror as shwon in figure. Light from a very far away source falls on the lens. An observer is situated some where in between lens and mirror, and observer is looking towards mirror. The observer will see the image behind teh mirror at a distance.
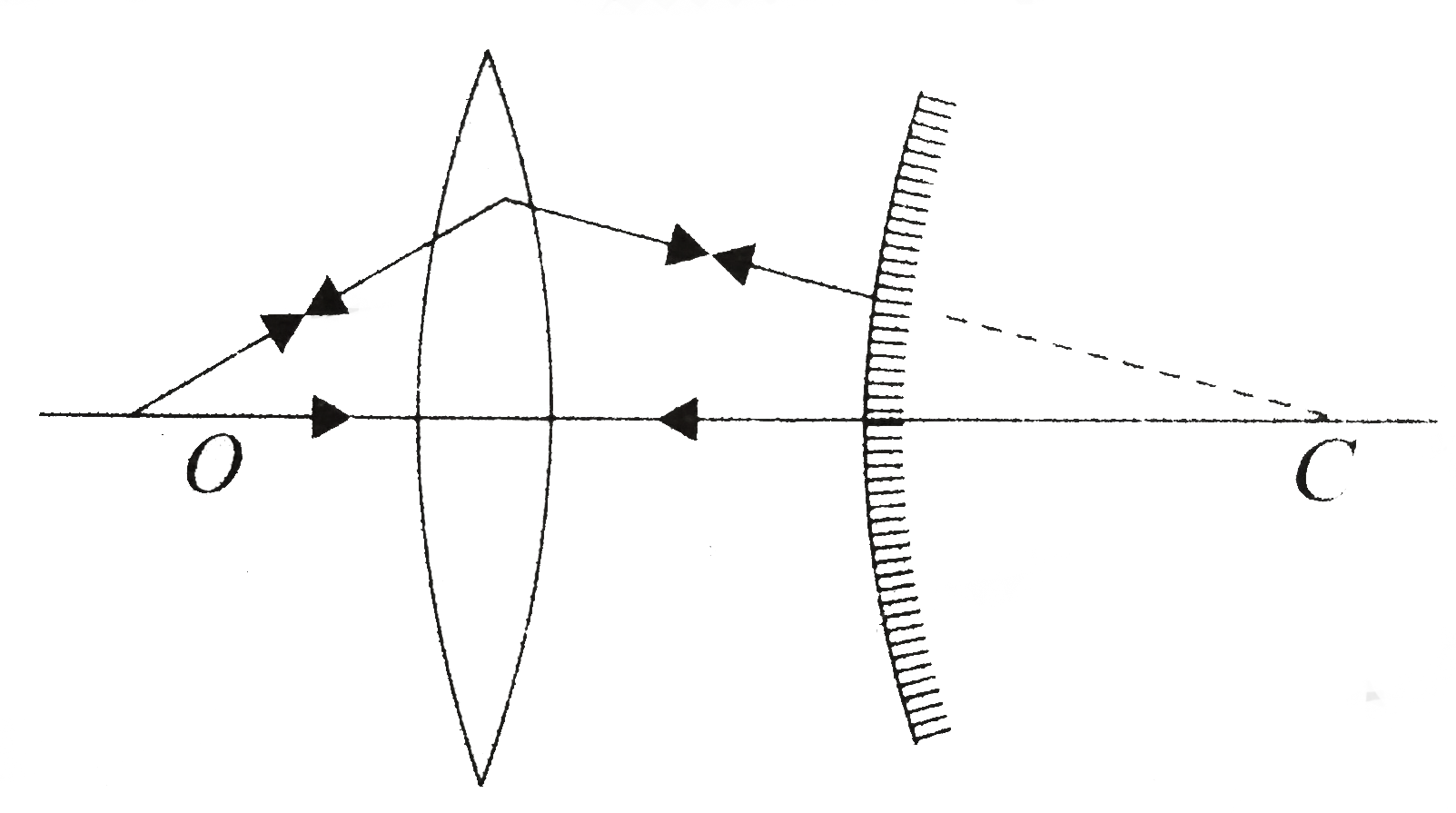
View SolutionAn object if placed at a distance of 15cm from a convex lens of focal length 10cm on the other side of the lens, a convex mirror is placed at its foxus such that the image formed by combination coincides with the object itself. Find the focal length of concave mirror.
View SolutionA point source of light is placed 60 cm away from screen. Intensity detected at point P is `I` . Now a diverging lens of focal length 20cm is placed 20cm away from S between S and P. The lens transmits `75%` of light incident on it. Find the new value intensity at P.

View SolutionA point source of light S is placed on the axis of a lens of focal length 20cm at a distance 25cm from lense. A screen is placed normal to the axis of lens at a distance x from it (treat all rays as paraxial). Identify the true or false statements.
a. As x is increased from zero , intensity continuously decreases.
b. As x is increased from zero, intensity first increases then decreases.
c. Intensity at center of screen for `x =90 cm` and `x=110 cm` is same.
View SolutionA converging lens and a converging mirror are placed with their principal axis coinciding. Their separation equals 40cm. A point source S is placed on the principal axis at a distance of 12 cm from the lens as shown in Fig. It is found that the final beam comes out parallel to the principal axis. Focal length of the lens equals 15 cm. Find the focal length of the mirror.

View SolutionA thin bi-convex lens made up of glass of refractive index `3//2` is placed is front of a plane mirror. The space between the lens and the mirror is filled with water of refractive index `4//3` . The radii of curvatures of the lens are `R_(1)=15cm` and `R_(2)=25 cm ` . A point object is placed at distance x from the surface whose curvature is `R_(1)`. The distance x is greater than the separation between the lens and the mirror. Find the value of x so that image must coincide with the object.
View SolutionA convex lens is held directly above a con lying on a table and forms an image of it. After the lens has been moved vertically a distance equal to its focal length, it forms another image of the coin equal in size with the previous image. If the diameter of the coin is 16 mm, what is the diameter in milimeters of the image?
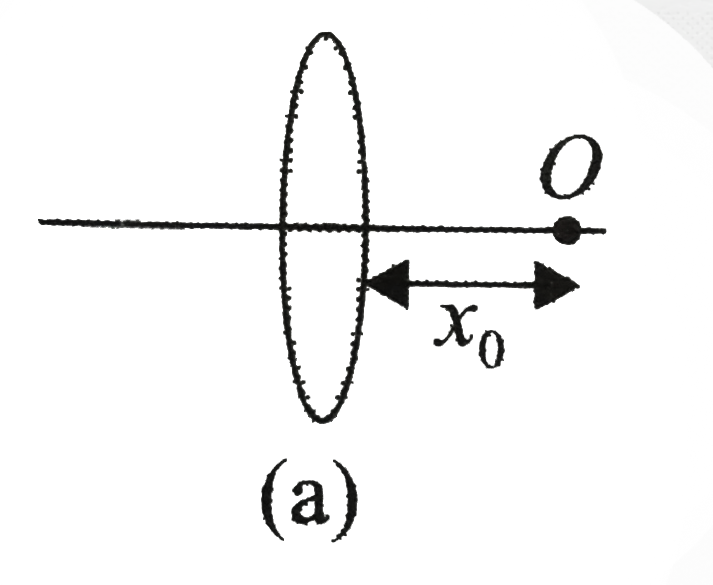
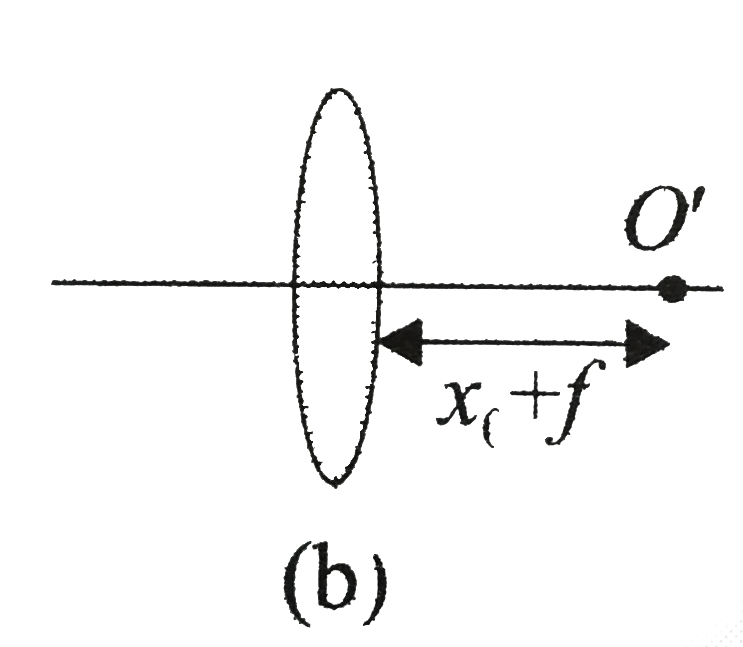
View SolutionA lens has a power of `+-` diopeters in air. What will be its power if completely immersed in water? `(._amu_(w)=4//3 and _amu_(g)=3//2)`
View Solution(a) A screen is kept at a distance of 1m from the object. A converging lens between the object and the screen, when placed at any of the two positions which are 60cm apart, forms a sharp image of the object on the screen. Find the focal length of the lens.
(b) In the two positions of the lens, lateral size of the image is 4cm and 9cm. Find the size of the object.
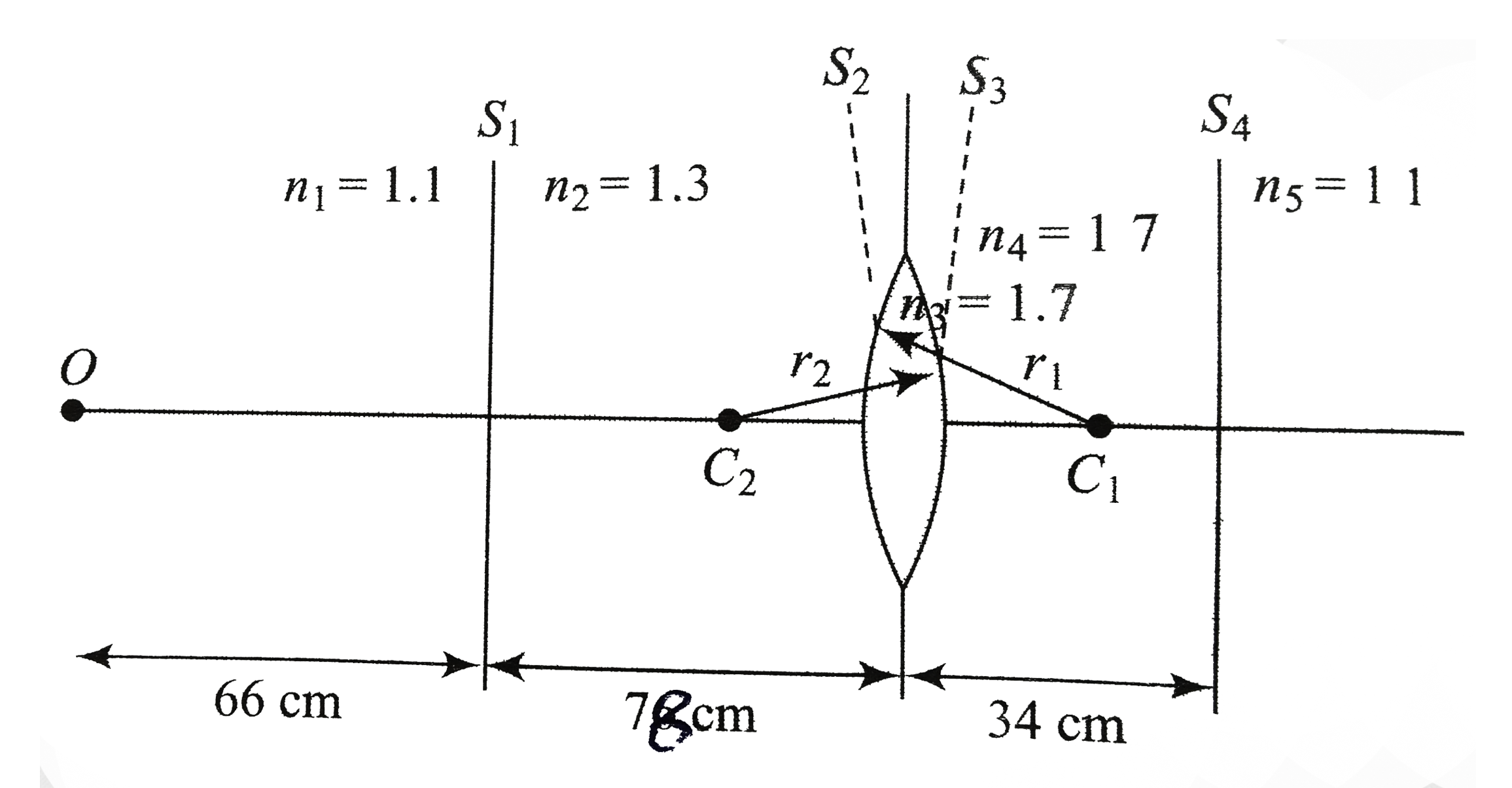
View SolutionA biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are `r_(1)=10cm` and `r_(2)=60cm` .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.
View SolutionA thin equiconvex lens made of glass of refractive index `3//2` and of focal length `0.3m` in air is sealed into an opening at one end of a tank filled with water `(mu=(3)/(2))`. On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis as shown in Figure. The separation between the lens and mirror is `0.8m. ` A small object is placed outside the tank in front of the lens at a distance oa `0.9m` from the lens along its axis. Find the position (relative to lens) of the image of the object formed by the system.

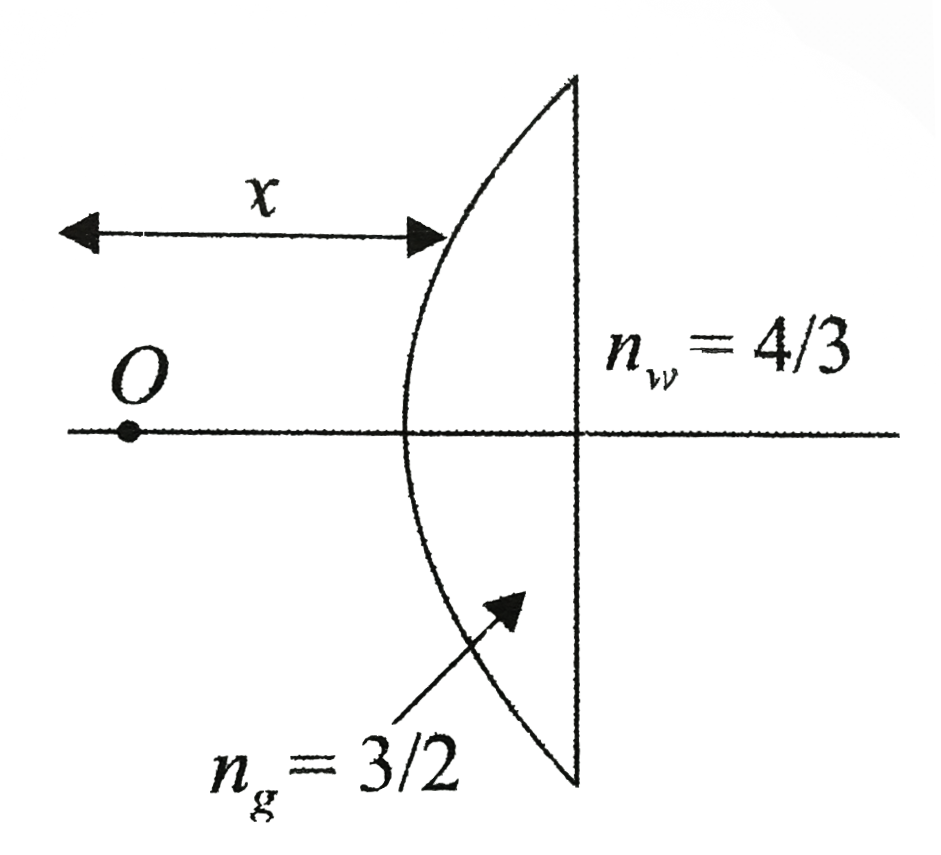
View SolutionObject O is kept in air in fron of a thin plano convex lens of radius of curvature 10cm. It's refractive index is `3//2` and the medium toward right of plane surface is water of refractive indec `4//3` . What should be the distance x of the object so that the rays become parrallel finall?
View SolutionThe diagram shows an equiconvex lens. What should be the condition on the refractive indices so that the lens becomes diverging?
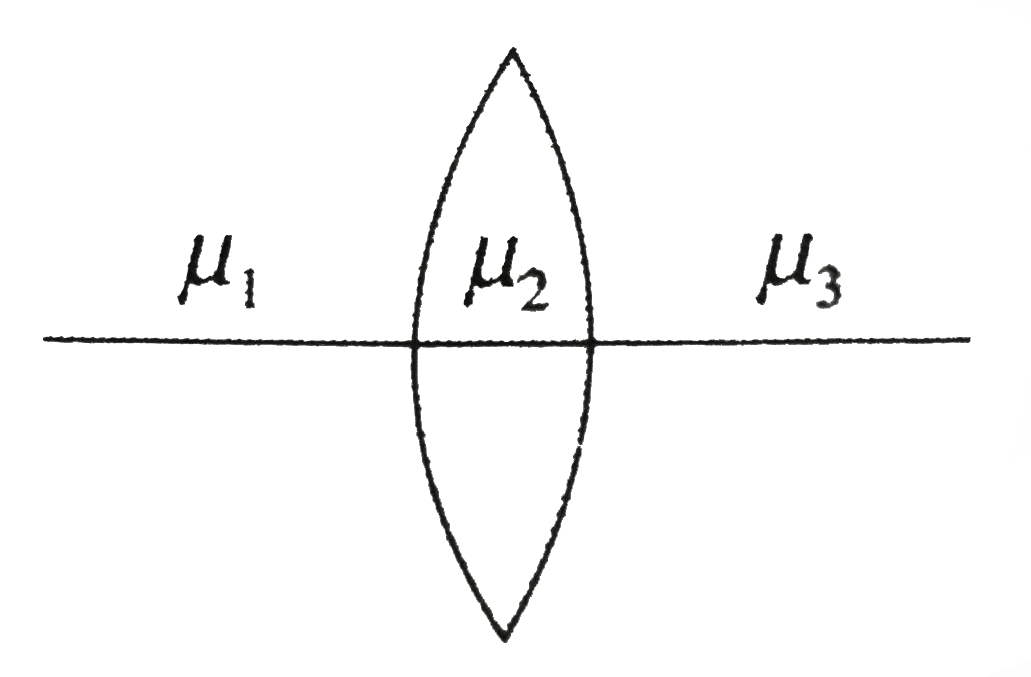
View SolutionFind the lateral magnification produced by the combination of lenses shown in Figure.
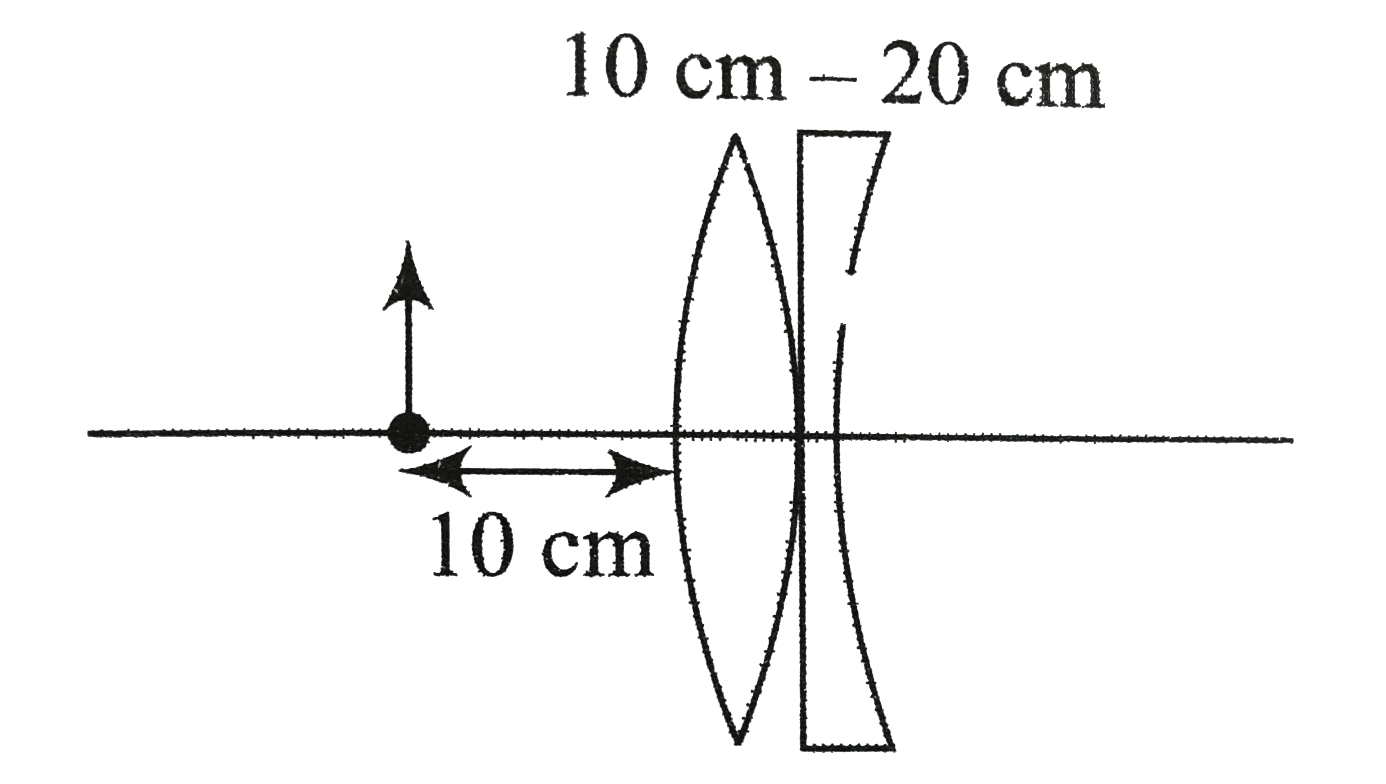
View SolutionFind the focal length of equivalent system shown in Figure.
View SolutionTwo convex lenses of focal length 20cm each are placed coaxially with a separation of 60cm between them. Find the image of a distant object formed by the combination by:
a. Using thin lense formul separately for the two lenses, and
b. Using the equivalent lens. Note that although the combination forms a real image of a distant object on the other side, it is equivalent to a diverging lens as far as the location of the final image is concerned.
View SolutionConsider a coaxial system of two thin convex lenses of focal length f each separated by a distance d. Draw ray diagrams for image formation corresponding to an object at infinity placed on the principal axis in the following cases: (a) `d lt f`,(b)`d=f`, (c ) `f lt d lt 2f`, (d) `d=2f`, and (e) `d gt 2f`. Indicate the nature of the combination (concave, convex or plane) in each case.
View Solution
Illustration questions and complete solutions for chapter GEOMETRICAL OPTICS of CENGAGE PHYSICS (HINGLISH) of Class 12