Complete Solutions to Solved Examples of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| CENGAGE PHYSICS | Solved Examples |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
In a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength `6000 Å` and intensity `(10//pi)` W `m^(-2)` is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness `2000 Å` and refractive index 1.5 for the wavelength of `6000 Å` is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
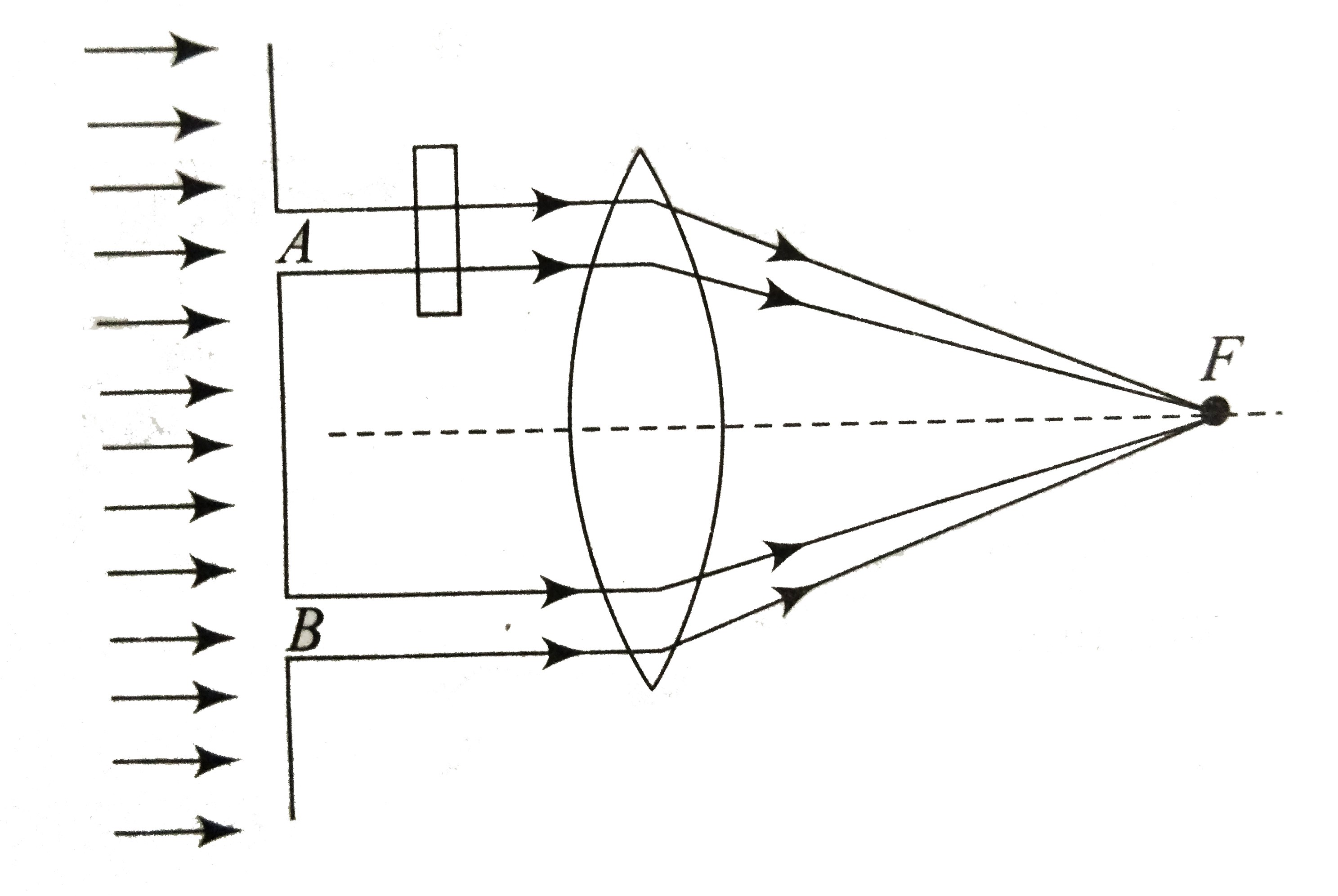
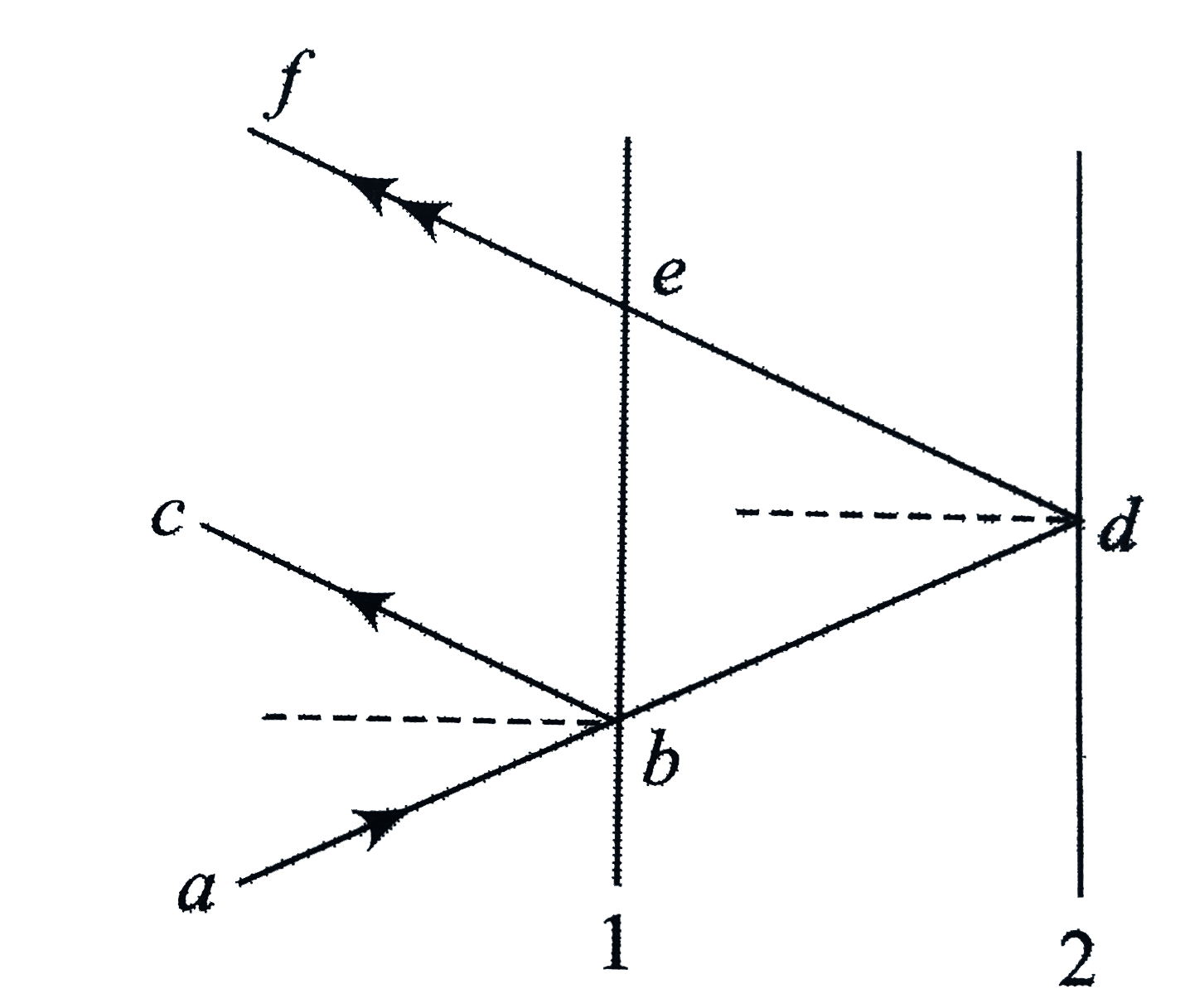
View SolutionA narrow monochromatic beam of light of intensity 1 is incident on a glass plate as shown in figure Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects `25%` of the light incident on it and transmits intensities in the interference pattern formed by two beams obtained after one reflection at each plate.
View SolutionIn figure S is a monochromatic point source emitting light of wavelength `lambda=500 nm`. A thin lens of circular shape and focal length `0.10 m` is cut into two identical halves `L_(1)` and `L_(2)` by a plane passing through a doameter. The two halves are placed symmetrically about the central axis `SO` with a gap of `0.5 mm`. The distance along the axis from `A` to `L_(1)` and `L_(2)` is `0.15 m`, while that from `L_(1)` and `L_(2)` to `O` is `1.30 m`. The screen at `O` is normal to `SO`.
(a) If the `3^(rd)` intensity maximum occurs at point `P` on screen, find distance `OP`.
(b) If the gap between `L_(1)` and `L_(2)` is reduced from its original value of `0.5 mm`, will the distance `OP` increases, devreases or remain the same?

View SolutionA double-slit apparatus is immersed in a liquid of refractive index 1.33. in It has slit separation of 1 mm and distance between the plane of slits and screen is 1.33 m. The slits are illuminated by a parallel beam or light whose wavelength in air is `6300 Å.`
a. Calculate the fringe width.
b. One of the slits of the apparauts is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring the adjacent minimum on the axix.
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index `1.4` while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index `1.7` interference pattern is observed using light of wavelength `5400 Å`
It is found that point P on the screen where the central maximum `(n = 0)` fell before the glass plates were inserted now has `3//4` the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
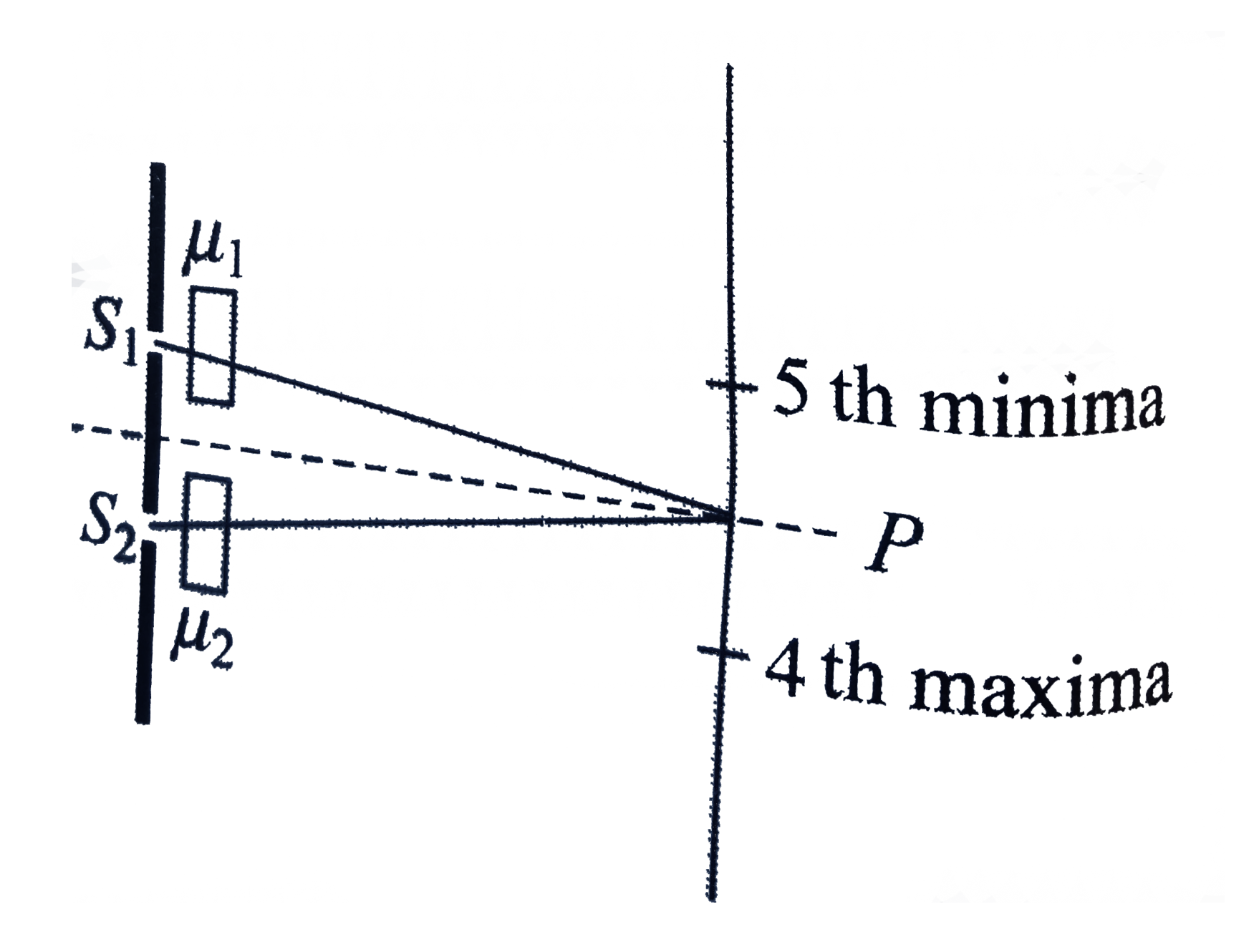 .
.
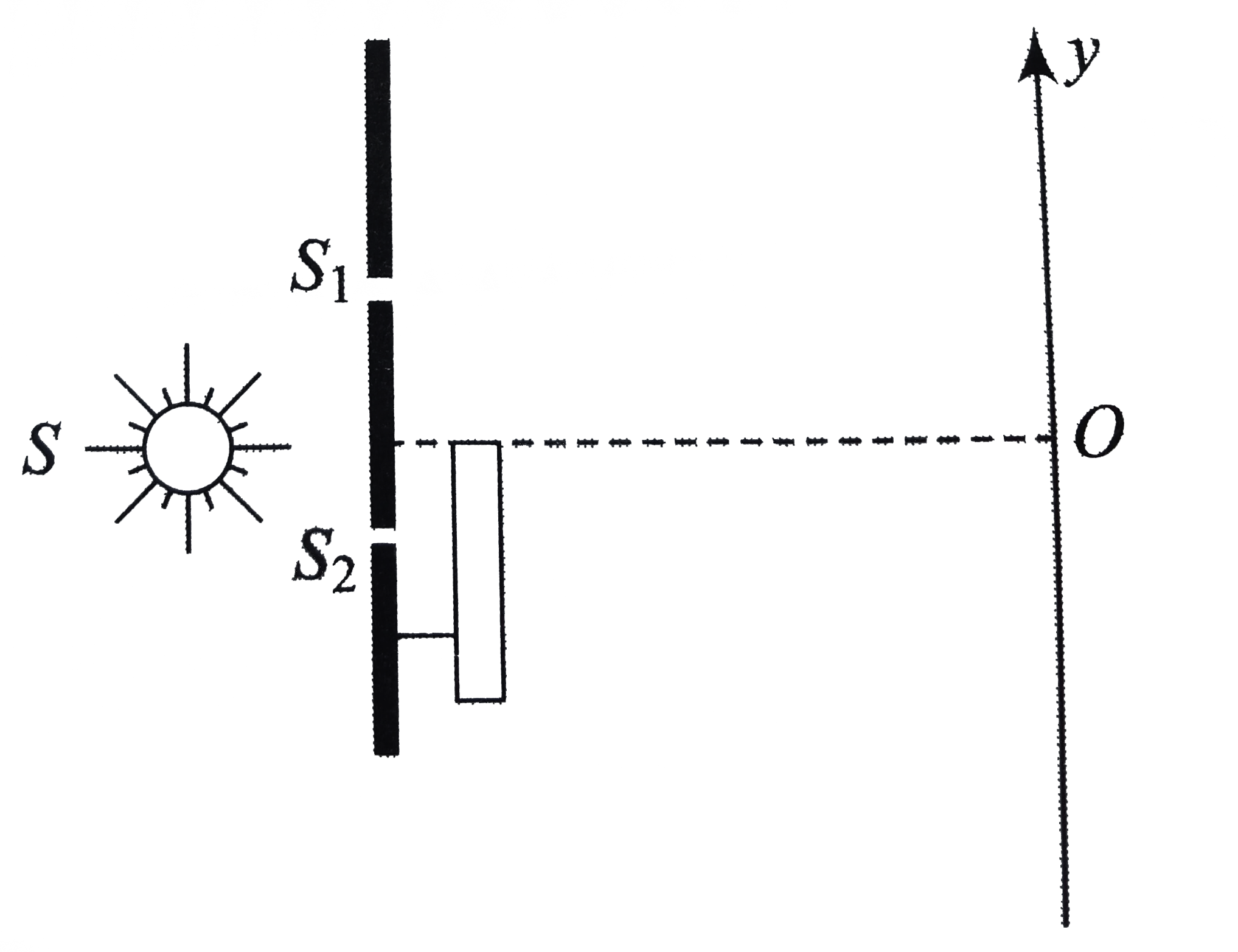
View SolutionThe Young's double-slit experiment is done in a medium of refractive index `4//3`. A light of 600 nm wavelength isfalling on the slits having 0.45 mm separation. The lower shift `S_(2)` is covered by a thin glass sheet of refractive index. 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in Figure
a. Find the location of central maximum (bright fringe with zero path difference) on the y-axis.
b. Find the light intensity of point O relative to the maximum fringe intensity.
c. Now , if 600 nm light is replaced by white light of range 400 - 700 nm, find the wavelengths of the light that from maxima exaclty at point O.
(All wavelength in the problem are for the given medium of refractive index `4//3` Ignoe dispersion.)
View SolutionA glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength `lambda` travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If `lambda = 648 nm`, obtain the least value of `t ("in" 10^(-8)m )` which the rays interface constructively.
View SolutionA vessel ABCD of `10 cm` width has two small slits `S_(1)` and `S_(2)` sealed with idebtical glass plates of equal thickness. The distance between the slits is `0.8 mm`. POQ is the line perpendicular to the plane AB and passing through O, the middle point of `S_(1)` and `S_(2)`. A monochromatic light source is kept at `S, 40 cm` below `P` and `2 m` from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line `OQ`. Now, a liquid is poured into the vessel and filled up to `OQ`. The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.

View SolutionA point sources `S` emitting light of wavelength `600nm` is placed at a very small height `h` above the flat reflecting surface `AB`(see figure).The intensity of the reflected light is`36%` of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance `D` from it.
(A)What is the shape of the interference fringes on the screen?
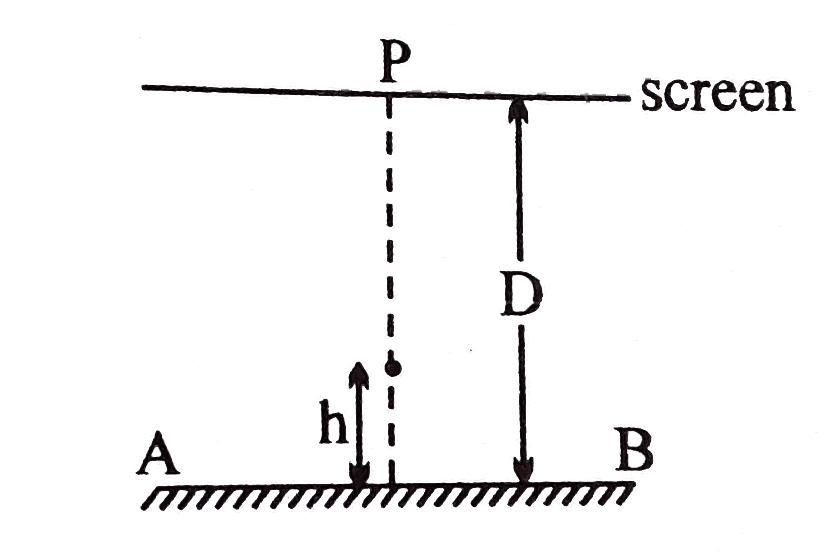
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point `P` (shown in the figure) (c) if the intenstities at point `P` corresponds to a maximum,calculate the minimum distance through which the reflecting surface `AB` should be shifted so that the intensity at `P` again becomes maximum.
View SolutionA prism `(mu_(P)=sqrt(3))` has an angle of prism `A=30^(@)`.A thin film `(mu_(f)=2.2)` is coated on face `AC` as shown in the figure.Light of wavelength `550nm` is incident on the face `AB`at`60^(@)`angle of incidence,find
(I)the angle of its emergence from the face`AC`and
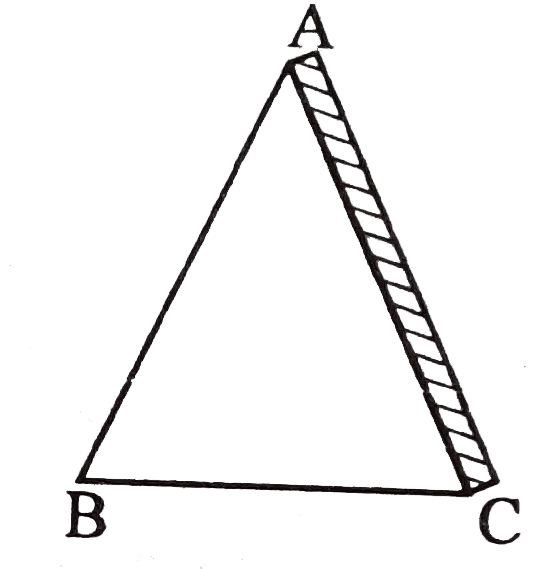
(ii)the minimum thickness (in mn) of the film for which the emerging light is of maximum possible intensity.
View Solution
Solved Examples questions and complete solutions for chapter WAVE OPTICS of CENGAGE PHYSICS (HINGLISH) of Class 12