Complete Solutions to Single Correct of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Microwaves from a transmitter are directed normally toward a plane reflector. A detector moves along the normal to the reflector. Between positionsof 14 m successive maxima the detector travels a distance 0.14 m. The frequency of the transmitter is `(c = 3 xx 10^(8) m s^(-1))`.
View SolutionIn Young's double-slit experiment, the separation between the slits is d, distance between the slit and screen is `D (D gt gt d)`, In the interference pattern, there is a maxima exactly in front of each slit. Then the possilbe wavelength(s) used in the experiment are
View SolutionIn a double-slit experiment, two parallel slits are illuminated first bylight of wavelength 400 nm and then by light of unknown wavelength. The fourth-order dark fringe resulting from the known wavelength of light falls in the same place on the screen as the second-order bright fringe from the unknown wavelength. The value of unknown wavelength of light is
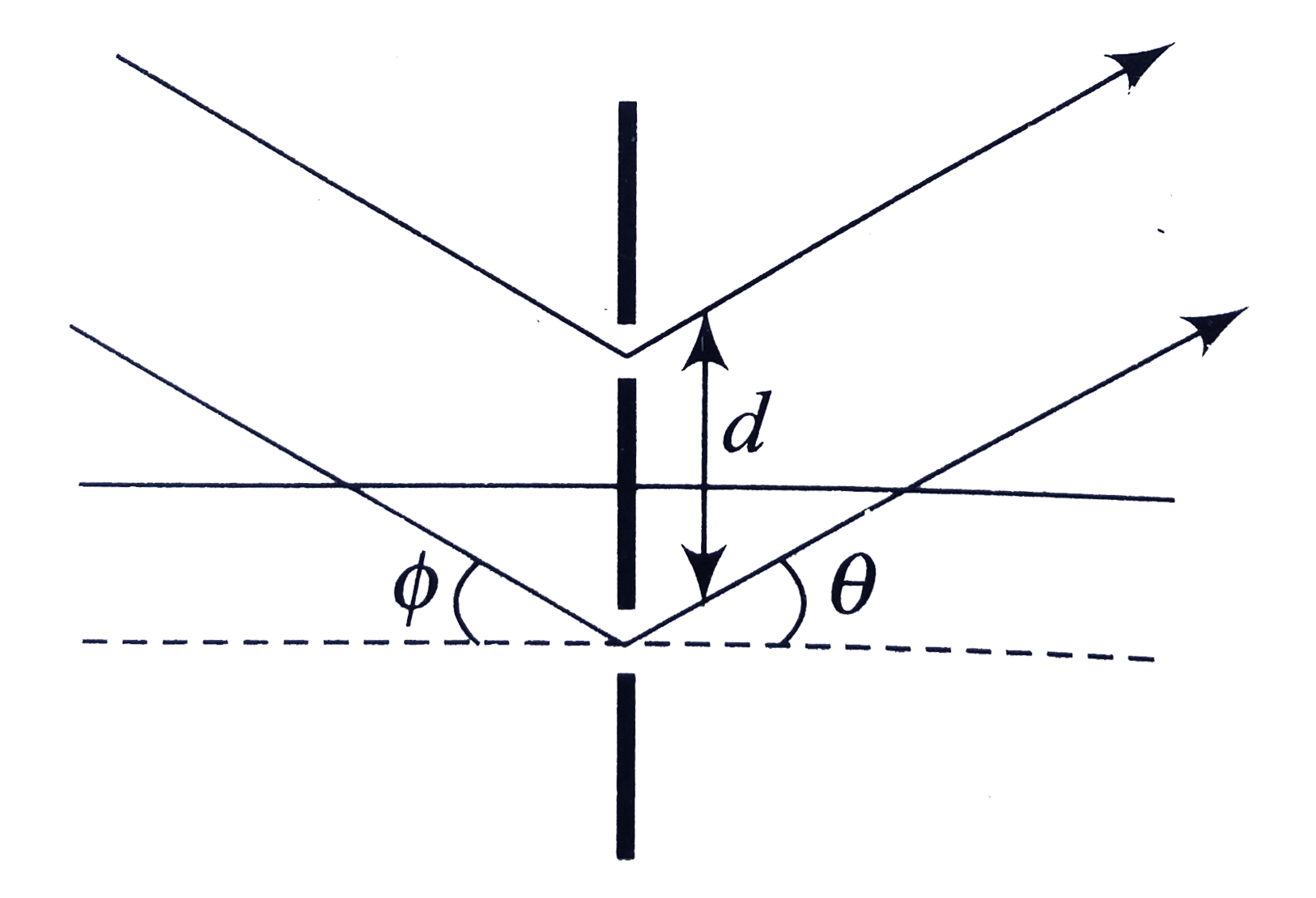
View SolutionLight is incident at an angle `phi` with the normal to a plane containing two slits of separation d. Select the expression that correctly describes the positions of the interference maxima in terms of the incoming angle `phi` and outgoing angle `theta`.
View SolutionIn Young's double-slit experiment, the slit are illuminated by monochromatic light. The entire set-up is immersed in pur water. Which of the following act cannot restore the oringinal fringe width?
View SolutionBlue light of wavelength 480 nm is most strongly reflected off a thin film of oil on a glass slab when viewed near normal incidence. Assuming that the index of refraction of the oil is 1.2 and that of the glass is 1.6, what is the minimum thickness of the oil film (other then zero)?
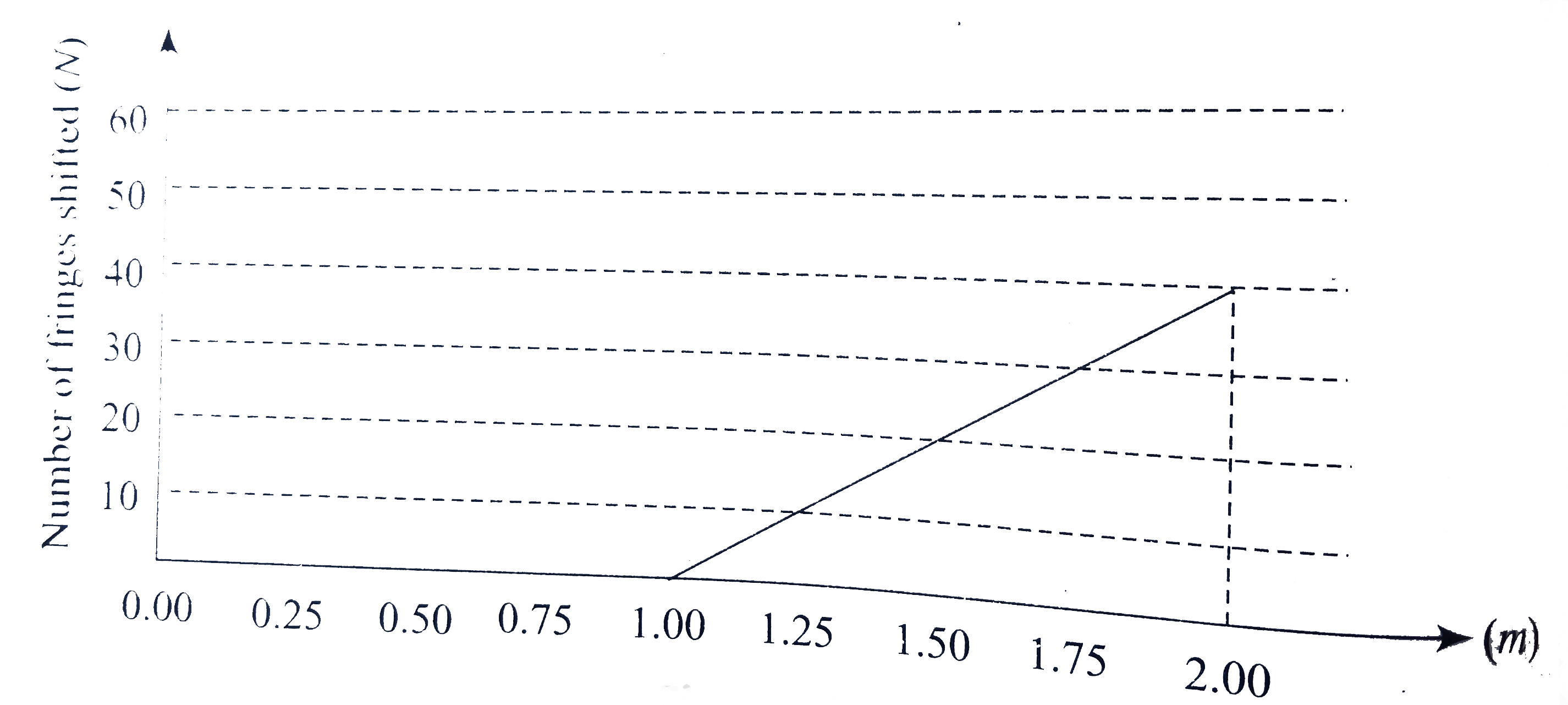
View SolutionThe slits in a double-slit interference experiment are illuminated by orange light `(lambda = 60 nm)`. A thin transparent plastic of thickness t is placed in front of one of the slits. The nunber of fringes shifting on screen is plotted versus the refractive index `mu` of the plastic in graph shown in figure. The value of t is
View SolutionIn a YDSE with identical slits, the intensity of the central bright fringe is `I_(0)`. If one of the slits is covered, the intensity at the same point is
View SolutionThe maximum intensity in young's double-slit experiment is `I_(0)`. Distance between the slit is `d = 5 lambda`, where `lambda` is the wavelength of monochromatic light used in the experiment. What will be the intensity of light in front of one of the slits on a screen at a distance `D = 10 d`?
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at separation x `(lt lt R)` symmetrical about the center of the circle. The sources emit identical wavelength `lambda` each. The number of points on the circle of maximum intensity is `(x = 5 lambda)`
View SolutionIn Young's double-slit experiment `d//D = 10^(-4)` (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit `I_(0)`. Then, the distance of point P from the central maximum is `(lambda = 6000 Å)`
View SolutionTo produce a minimum reflection of wavelength near the middle of visible spectrum (550 nm), how thick should a coating of `MgF_(2) (mu = 1.38)` be vaccum-coated on a glass surface?
View SolutionA thin film of refractive index 1.5 and thickness `4 xx 10^(-5)` cm is illuminated by light normal to the surface. What wavelength within the visible spectrum will be intensified in the reflected beam?
View SolutionA plane wave of monochromatic light falls normally on a uniform thin or oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive is observed for `lambda = 5000 Å` and `lambda = 1000 Å` and for no other wavelength in between. If `mu` of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
View SolutionA light ray of frequency v and wavelength `lambda` enters a liquid of refractive index `3//2`. The ray travels in the liquid with
View SolutionIn a double-slit experiment, instead of taking slits of equal width, one slit is made twice as wide as the other Then in the interference pattern
View SolutionTwo light waves having the same wavelength `lambda` in vacuum are in phase initially. Then the first ray travels a path of length `L_(1)` through a medium of refractive index `mu_(1)`. Then second ray travels a path of length `L_(2)` throug a medium of refractive index `mu_(2)`. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View SolutionLight of wavelength `lambda = 5890 Å` fall on a double-slit arrangement having separation `d = 0.2 mm`. A thin lens of focal length `f = 1 m` is placed near the slits. The linear separation of fringes on a screen placed in the focal plane of the lens is
View SolutionIn Young's double-slit experiment, the two slits act as coherent sources of equal amplitude `A` and of wavelength `lamda`. In another experiment with the same set-up the two slits are sources of equal amplitude `A ` and wavelength `lamda`, but are incoherent. The ratio of the intensity of light at the midpoint of the screen in the first case to that in the second case is....
View SolutionIn Young'double-slit interference experiment, if the slit separation is made threefold, the fringe width becomes
View SolutionSources 1 and 2 emit lights of different wavelengths whereas sources 3 and 4 emit light of different intensities.
The coherence
View SolutionIf one of the two slits og Young's double-slit experiment is painted so that it transmits half the light intensity as the second slit, then
View SolutionA wave front AB passing through a system C emerges as DE. The system C could be
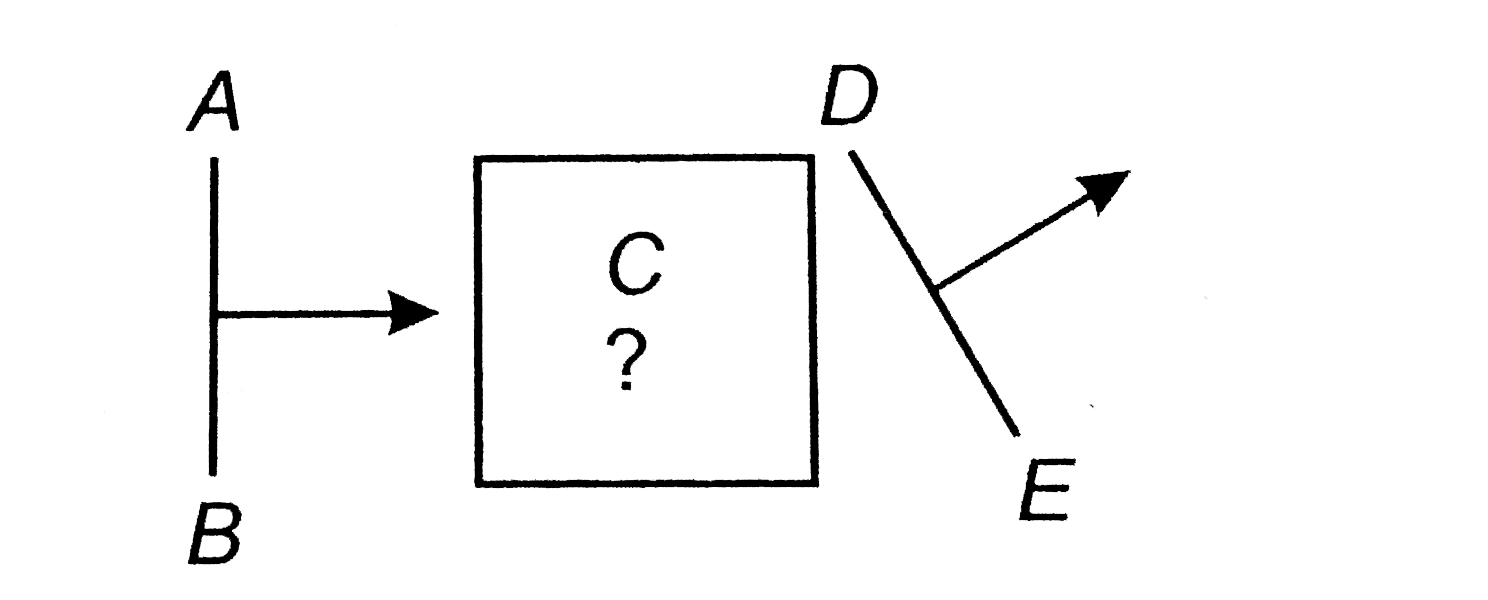
View SolutionFigure shows wavefront P Passing through two systems A and B, and emerging as Q and then as R. Then systems A and B could, respectively, be

View SolutionLight waves travel in vacuum along the y-axis. Which of the following may represent the wavefront?
View SolutionIn Young's double-slit experiment, the y-coordinate of central maxima and 10th maxima are 2 cm and 5 cm, respectively, When the YDSE apparatus is immersed in a liquid of refreactive index 1.5, the corresponding y-coordinates will be
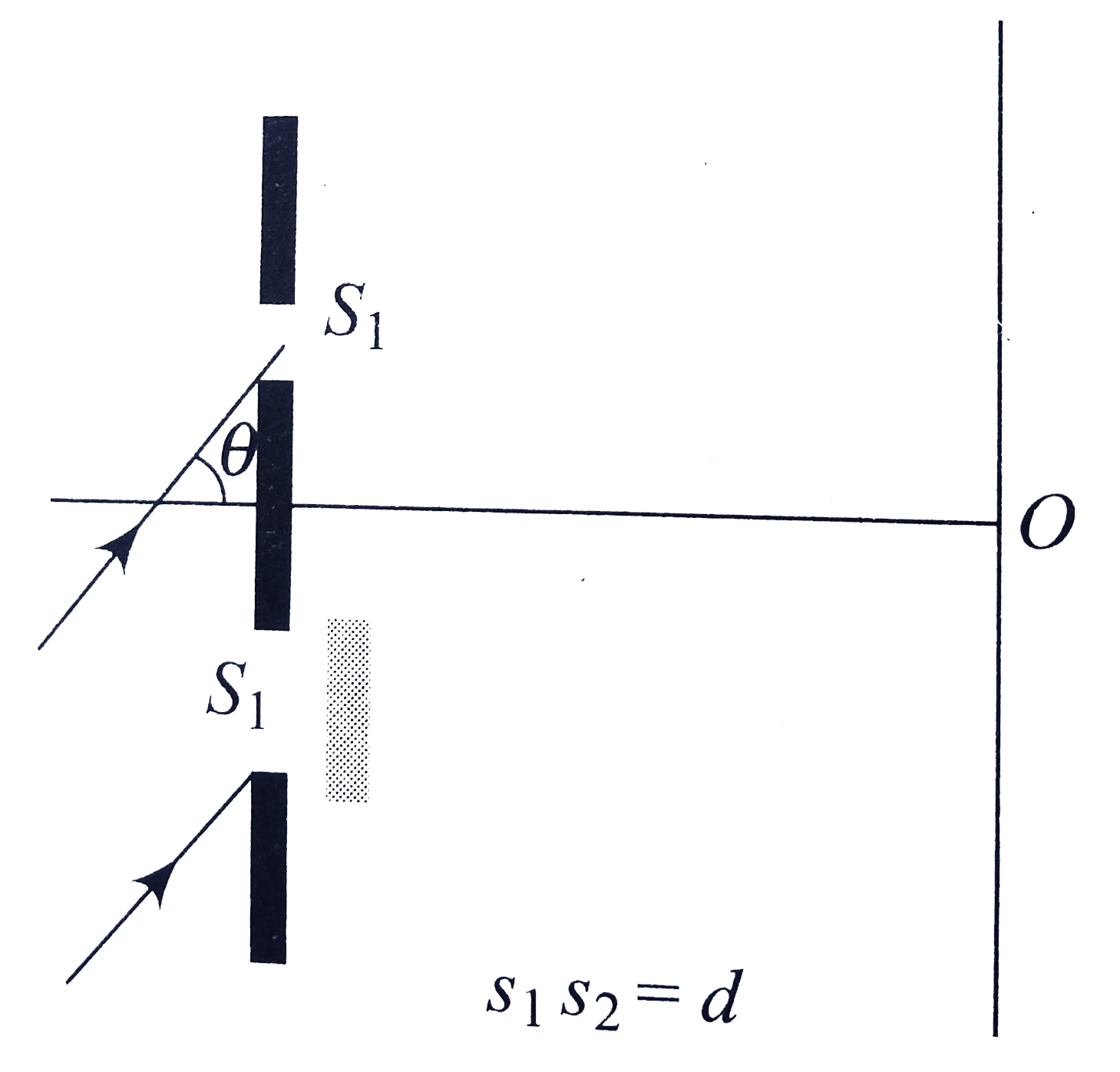
View SolutionA monochromatic beam of light fall on YDSE apparatus at some angle (say `theta`) as shown in figure. A thin sheet of glass is inserted in front of the lower slit `s_(2)`. The central bright fringe (path difference `= 0`) will be obtained
View SolutionA plate of thickness t made of a material of refractive index `mu` is placed in front of one of the slits in a double slit experiment. (a) Find the changes in he optical path due to introduction of the plate. (b) Wht should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ? Wavelength of the light used is `lamda`. Neglect any absorption of light in the plate.
View SolutionIn Young's double-slit experiment, how many maxima can be obtained on a screen (including the central maximum) on both sides of the central fringe `(lambda = 2000 Å)`?
View SolutionYoung's double slit experiment is made in a liquid. The tenth bright fringe in liquid lies in screen where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
View SolutionWhat happens to the interference pattern if the two slits in Young's experiment are illuminated by two independent sources such as two sodium lamps S and S' as shown in figure
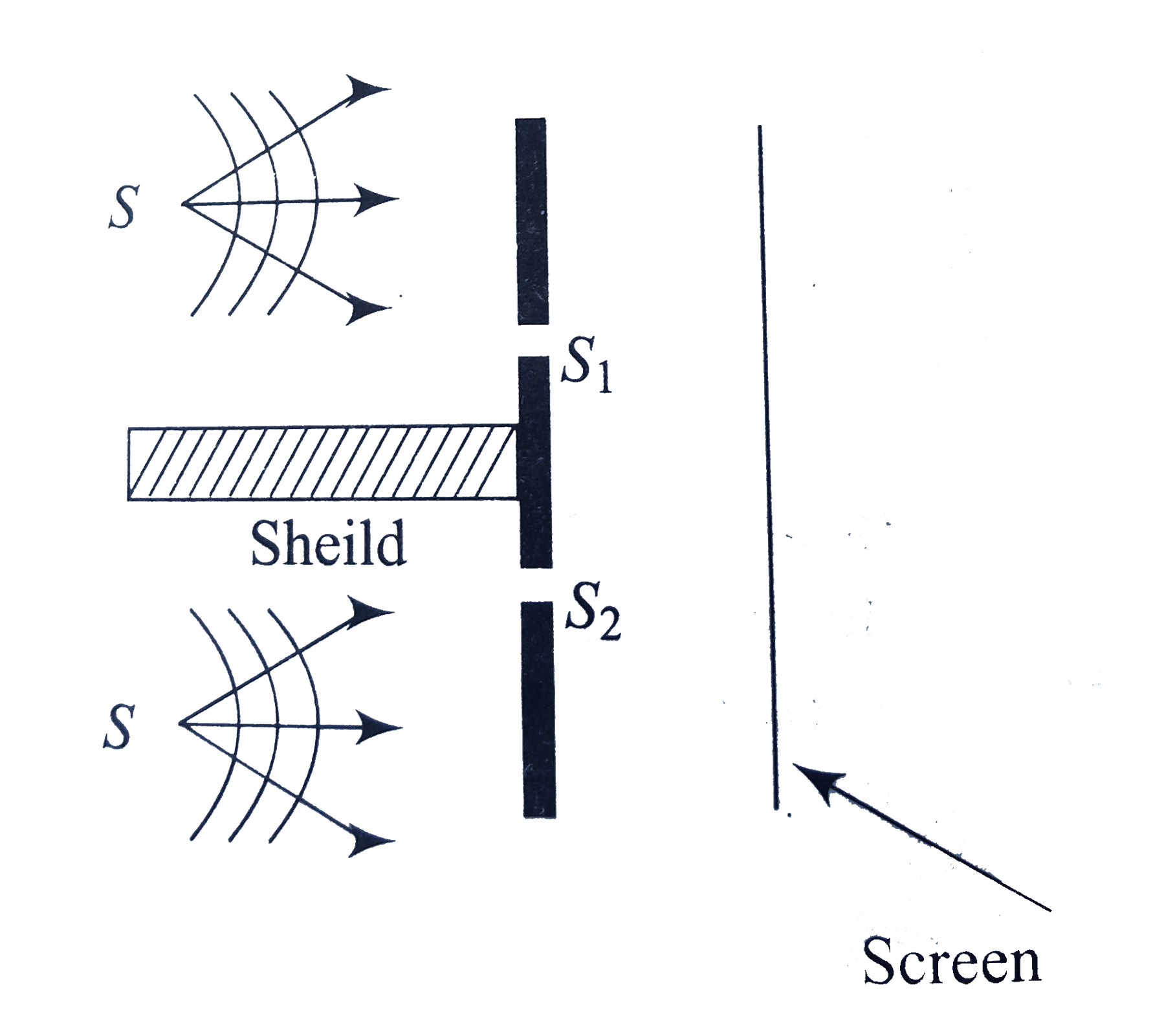
View SolutionIn Young's double-slit experiment, 30 fringes are obtained in the field of view of the observing telescope, when the wavelength of light used is `4000 Å`. If we use monochromatic light of wavelength `6000 Å`, the number of fringes obtained in the same field of view is
View SolutionIn a standard Young's double-slit experiment with coherent light of wavelength 600 nm, the fringe width of the fringes in the central region (near the central fringe, `P_(0)`) is observed it to be 3 mm. An extremely thin glass plate is introduced to be displaced by 11 mm. Another thin plate is placed before the second slit and it is observed that the fringe are now displaced by an additional 12 mm. If the additional optical path lengths introduced are `Delta_(1)` and `Delta_(2)` then
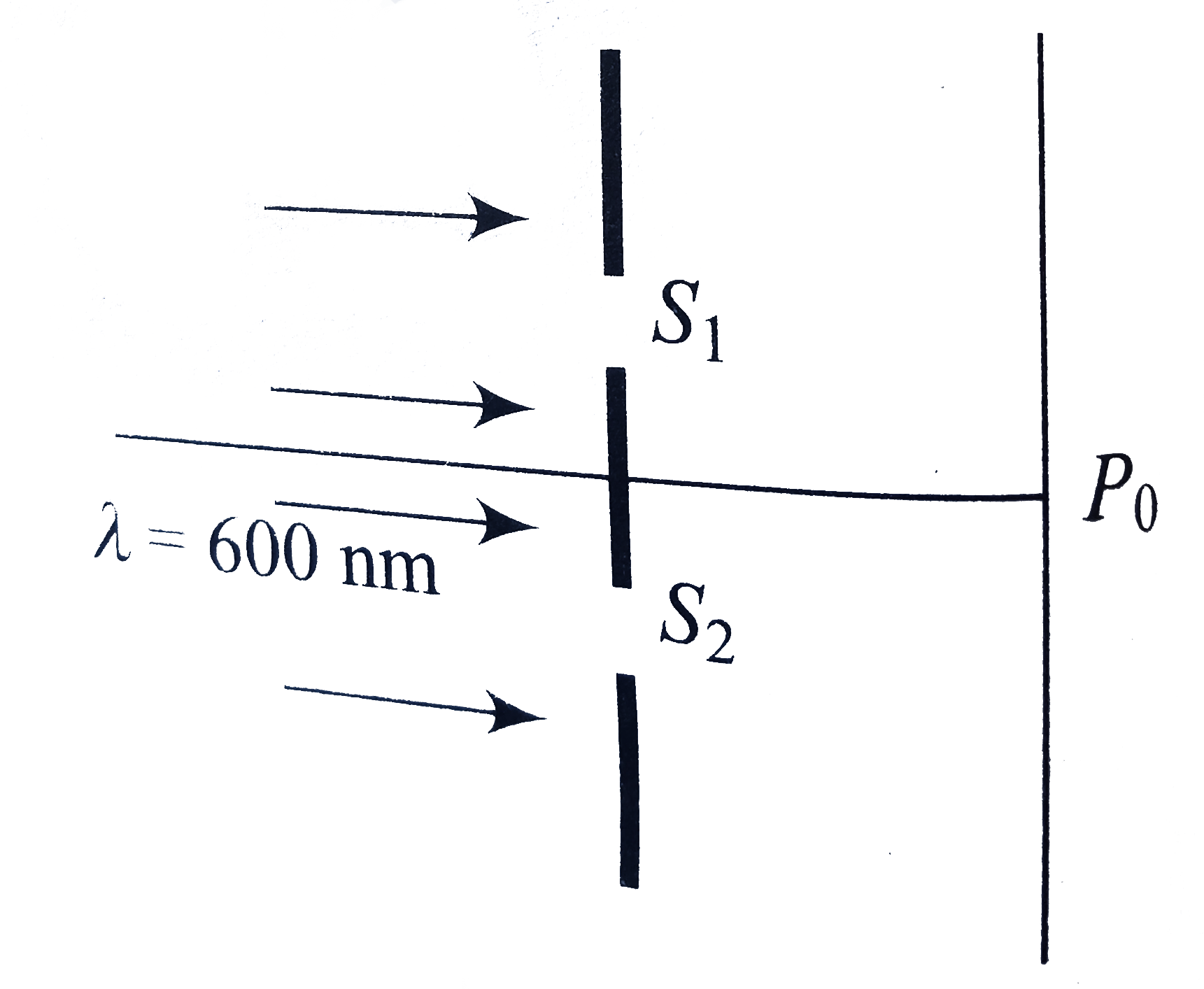
View SolutionIn Young's doulbe-slit experiment the separation between two coherent sources `S_(1)` and `S_(2)` is d and the distance between the source and screen is D. In the interference pattern, it is found that exactly in front of one slit, there occurs a minimum. Then the possible wavelengths used in the experiment are
View SolutionLet `S_(1)` and `S_(2)` be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle `/_ S_(1) P S_(2) = theta`, then fringe width for the light of wavelength `lambda` will be
View SolutionIn a two slit experiment with white light, a white fringe is observed o a screen kept behind the slits When the screen in moved away by 0.05 m, this white fringe
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index `mu_1` as shown in figure. A thin transparent slab of refractive index `mu_2` is placed in front of the slit `s_2`. The magnitude of optical path difference at 'O' is
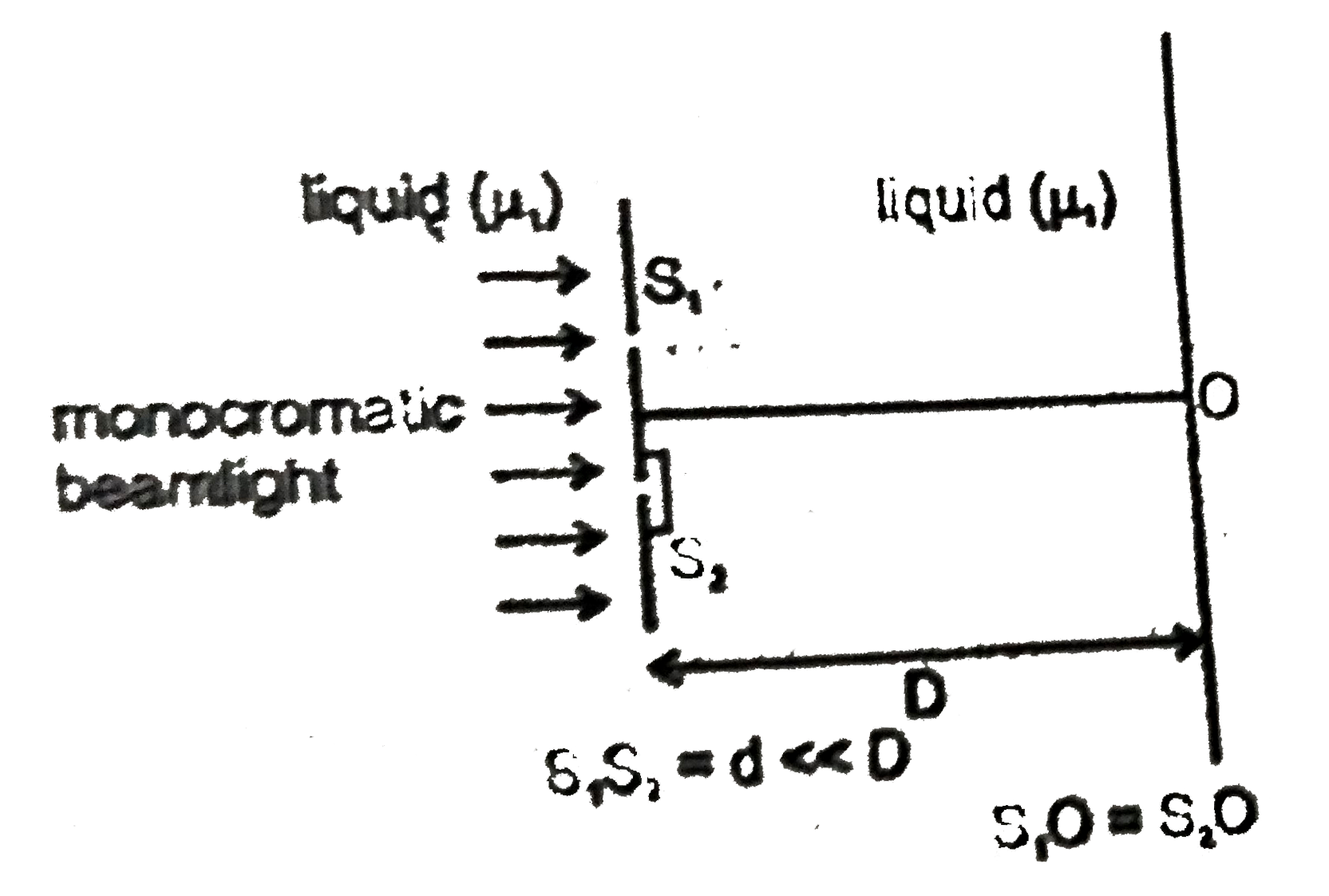
View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)

View SolutionMicrowaves from a transmitter are directed normally toward a plane reflector. A detector moves along the normal to the reflector. Between positions of 14 successive maxima the detector travels a distance 0.14 m. The frequency of the transmitter is `(c = 3 xx 10^(8) m s^(-1))`.
View SolutionIn a double-slit experiment, the slits are separated by a distance d and the screen is at a distance D from the slits. If a maximum is formed just opposite to each slit, then what is the order or the fringe so formed?
View SolutionA parallel beam of white light is incident on a thin film of air of uniform thickness. Wavlength `7200 Å` and `5400 Å` are observed to be missing from the spectrum of reflected light viewed normally. The other wavelength in the visible region missing in the reflected spectrum is
View SolutionTwo beams of ligth having intensities I and 4I interface to produce a fringe pattern on a screen. The phase difference between the beams is `(pi)/(2)` at point A and `pi` at point B. Then the difference between the resultant intensities at A and B is
View SolutionIn a Young's double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600nm is used. If the wavelength of light is changed to 400nm, number of fringes observed in the same segment of the screen is given by
View SolutionIn the ideal double-slit experiment, when a glass-plate(refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wave-length `lamda`), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View SolutionA double-slit experiment, arrangement produces interference fringes for sodium light `(lambda = 589 nm)` that have an angular separation of `3.50 xx 0^(-3)` rad . For what wavelength would the angular separation to `10%` greater?
View SolutionIn Young's double-slit experimetn, the intensity of light at a point on the screen, where the path difference is `lambda`,is `I` . The intensity of light at a point where the path difference becomes `lambda // 3` is
View SolutionTwo point sources separated by 2.0 m are radiating in phase with `lambda = 0.50 m`. A detector moves in a circular path around the two sources in a plane containing them. How many maxima are detected?
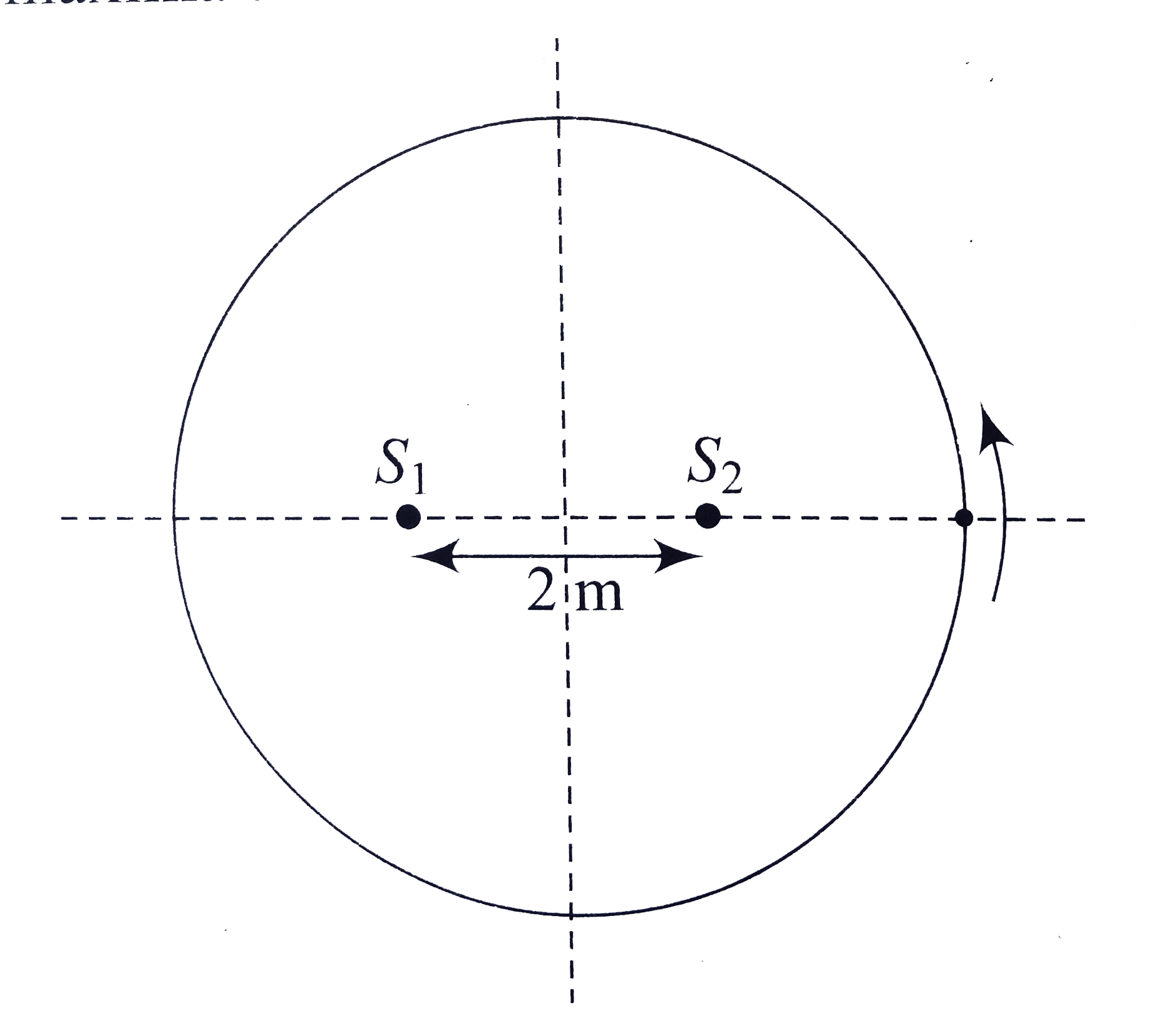
View SolutionIn YDSE, light of wavelength `lamda = 5000 Å` is used, which emerges in phase from two a slits distance `d = 3 xx 10^(-7) m` apart. A transparent sheet of thickness `t = 1.5 xx 106(-7) m`, refractive indes `n = 1.17`, is placed over one of the slits. Where does the central maxima of the interference now appear from the center of the screen? (Find the value of y?)
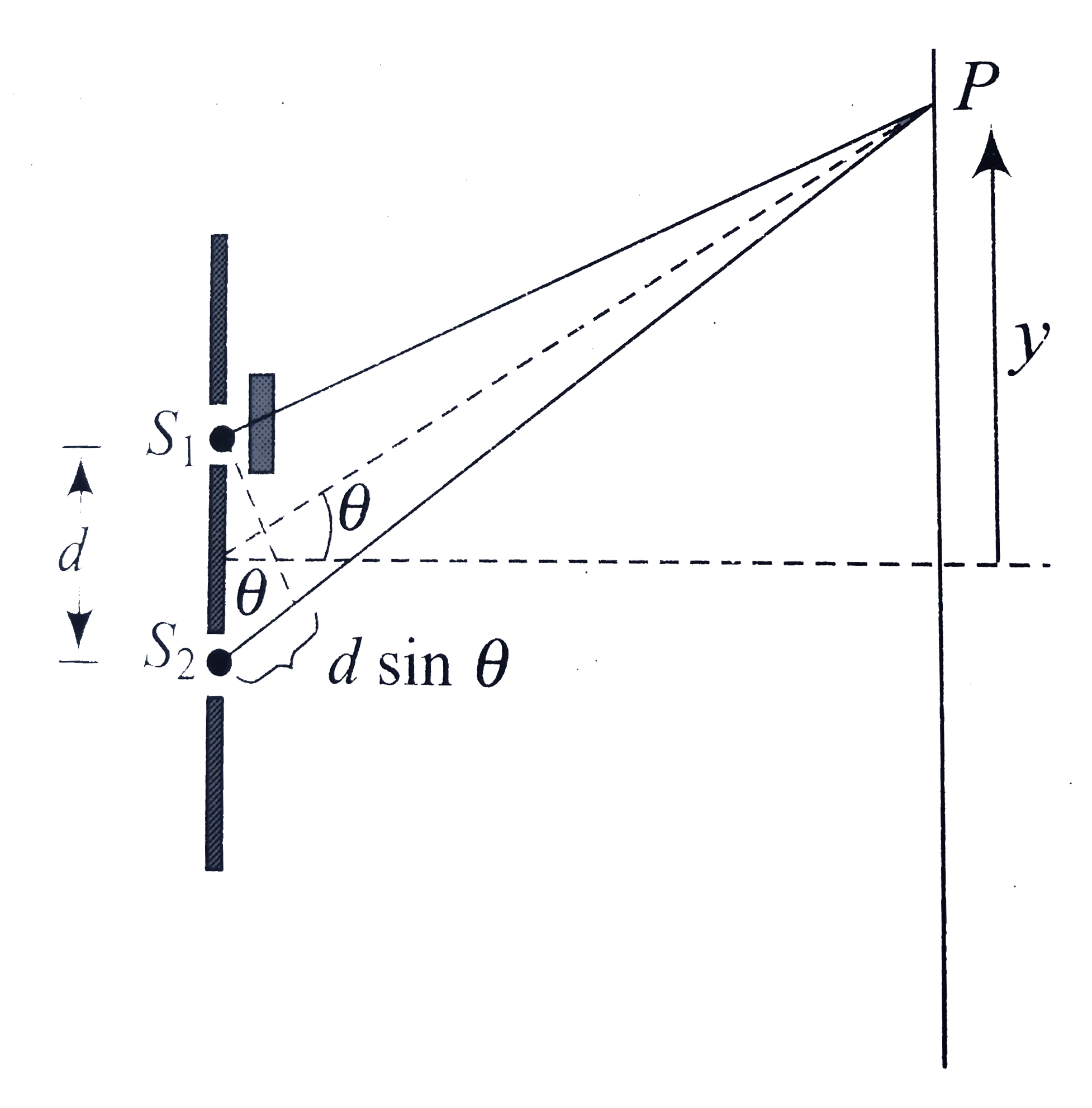
View SolutionA double-slit experiment is immersed in a liquid of refractive index 1.33. It has slit separation of 1 mm and distance between the plane of slits and screen is 1.33 m. The slits are illuminated by a parallel bam of light whose wavelength in air is `6830 Å`. Then the fringe width is
View SolutionIn Young's double-slit experiment, the slit separation is 0.5 mm and the screen is 0.5 m away from the slit. For a monochromatic light of wavelength 500 nm, the distance of 3rd maxima from the 2nd minima on the other side of central maxima is
View SolutionA light of wavelength `6000 Å` shines on two narrow slits separeted by a distance 1.0 mm and illuminates a screen at a distance 1.5 m away. When one slit is covered by a thin glass plate of refractive index 1.8 and other slit by a thin glass plate of refractive index `mu`, the central maxima shifts by 0.1 rad. Both plates have the same thickness of 0.5 mm. The value of refractive index `mu` of the glass is
View SolutionA plane wavefront travelling in a straight line in vacuum encounters a medium ofrefractive index m. At P, the shape of the wavefront is
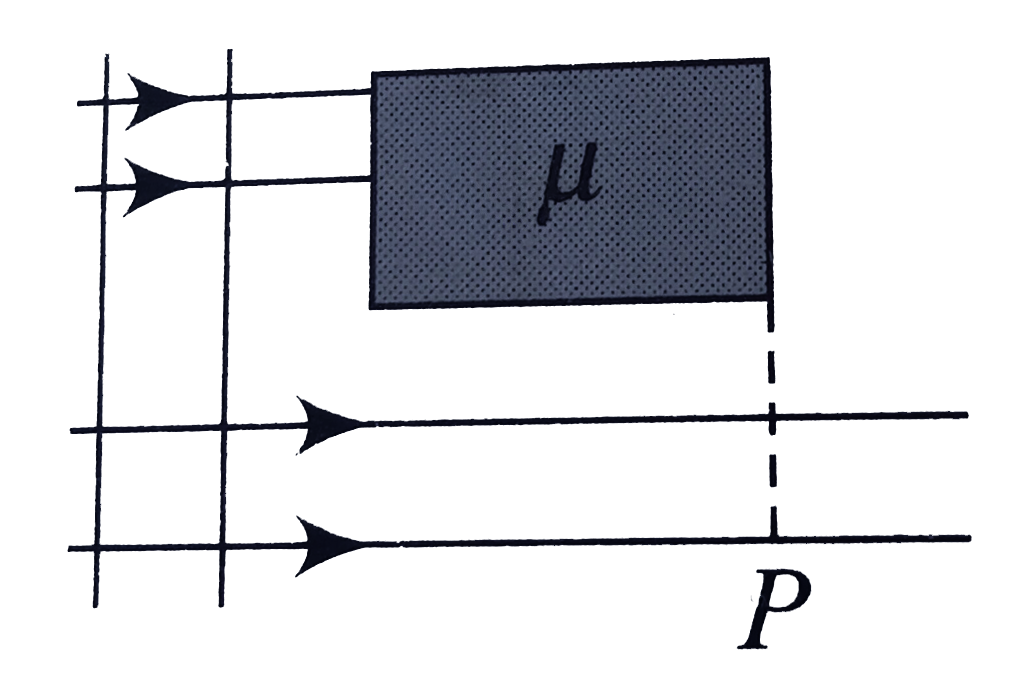
View SolutionIn Young's double-slit experiment, the wavelength of light was changed from `7000 Å` to 3500 Å`. While doubling the separation between the slits, which of the following is not true for this experiment?
View SolutionCalculate the wavelength of light used in an interference experiment from the following data: Fringe width = 0.03 cm. Distance between slits and eyepiece through which the interference pattern is observed is 1 m. Distance between the images of the virtural when a convex lens of focal length 16 cm is used at a distance of 80 cm from the eyepiece is 0.8 cm.
View SolutionIn Young's double-slit experiment the angular width of a fringe formed on a distant screen is `1^(@)`. The wavelength of light used is `6000 Å`. What is the spacing between the slits?
View SolutionIn a double-slit experiment, the slits are separated by a distance d and the screen is at a distance D from the slits. If a maximum is formed just opposite to each slit, then what is the order or the fringe so formed?
View SolutionIn a Young's double slit experiment using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the slits and screen is doubled. It is found that the distance between successive maxima now is the same as observed fringe shift upon the introduced of the mica sheet . Calculate the wavelength of the monochromatic light used in the experiment .
View SolutionIn YDSE, find the thickness of a glass slab `(mu=1.5)` which
should be placed in front of the upper slit `S_1` so that the central maximum now
lies at a point where 5th bright fringe was lying earlier (before inserting the
slab). Wavelength of light used is `5000 Å`.
View SolutionIn Young's double-slit experiment, the slit are 0.5 mm apart and the interference is observed on a screen at a distance of 100 cm from the slits, It is found that the ninth bright fringe is at a distance of 7.5 mm from the second dark fringe from the center of the fringe pattern. The wavelength of the light used is
View SolutionFigure shows two coherent sources `S_(1)` and `S_(2)` emitting wavelength `lambda`. The separation `S_(1) S_(2) = 1.5 lambda` and `S_(1)` is ahead in phase by `pi // 2` relative to `S_(2)` Then the maxima occur in direction `theta` given by `sin^(-1)` of
(i) 0 (ii) `1// 2` (iii) `-1//6` (iv) `-5 // 6`
Correct option are

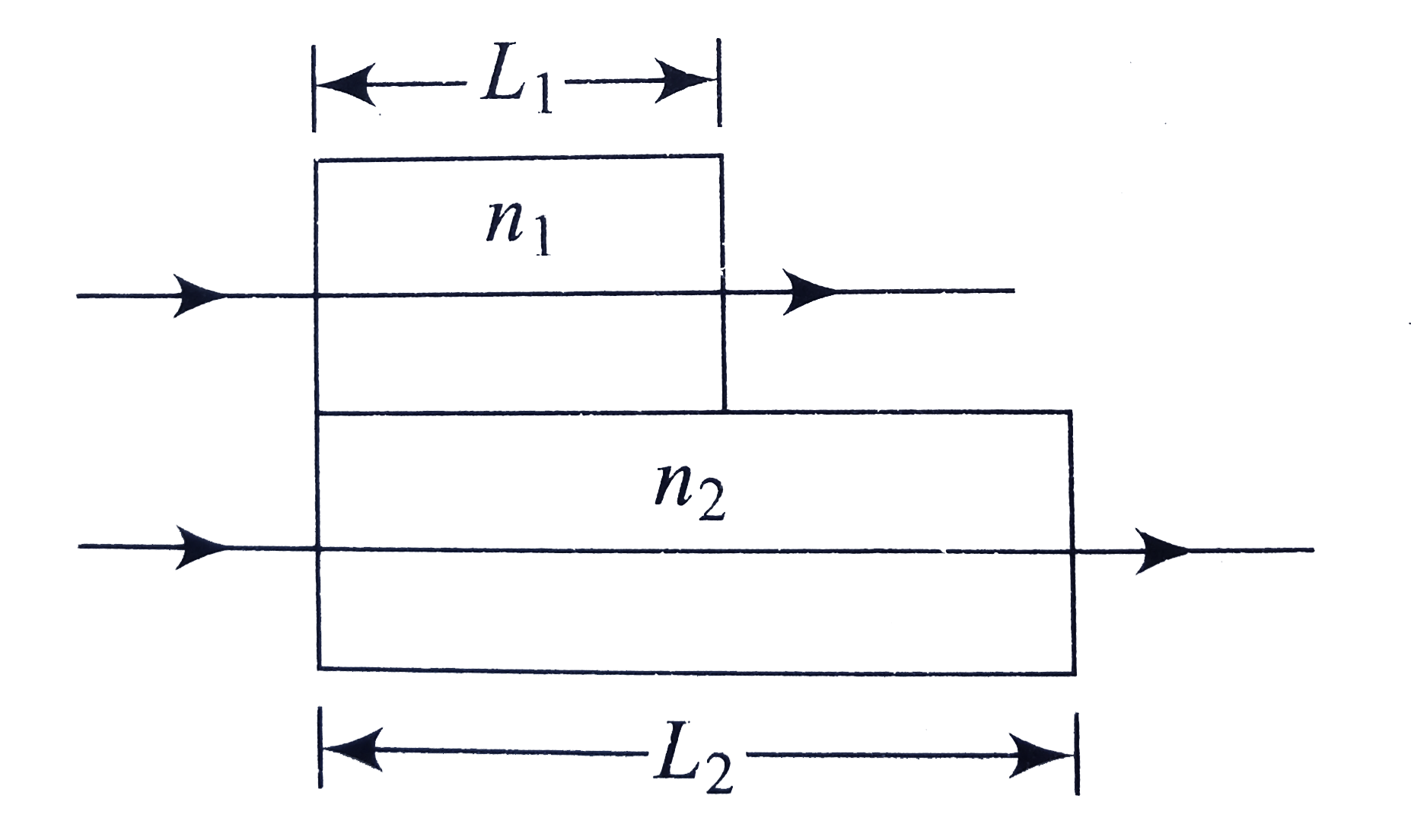
View SolutionTwo waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of `L_(1) = 3.5 mm` and `L_(2) = 5.0 mm` and indices of refraction `n_(1) = 1.7` and `n_(2) = 1.25` as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
View SolutionLight from a sources emitting two wavelengths `lambda_(1)` and `lambda_(2)` is allowed to fall on Young's double-slit apparatus after filtering one of the wavelengths. The position of interference maxima is noted. When the filter is removed both the wavelengths are incident and it is found that maximum intensity is produced where the fourth maxima occured previously. If the other wavelength if filtered, at the same location the third maxima is found. What is the raito of wavelength?
View SolutionThe wavefront of a light beam is given by the equation `x + 2y + 3x = c` (where c is arbitrary constant), then the angle made by the direction of light with the y-axis is
View SolutionAs shown in figure waves with identical wavelengths and amplitudes and which are intially in phase travel through difference media. Ray 1 travels through air and Ray 2 through a transparent medium for equal length L, in four different situations. Rays reach a common point on the screen. The number of wavelengths in length L is `N_(2)` for Ray 2 and `N_(1)` for Ray 1. In the following table, values of `N_(1)` and `N_(2)` are given for all four situations. The order or the situations according to the intensity of the light at the common point in descending order is Situations
1 2 3 4
`N_(1)` 2.75 1.80 3.00 3.25
`N_(2)` 2.75 2.80 3.25 4.00
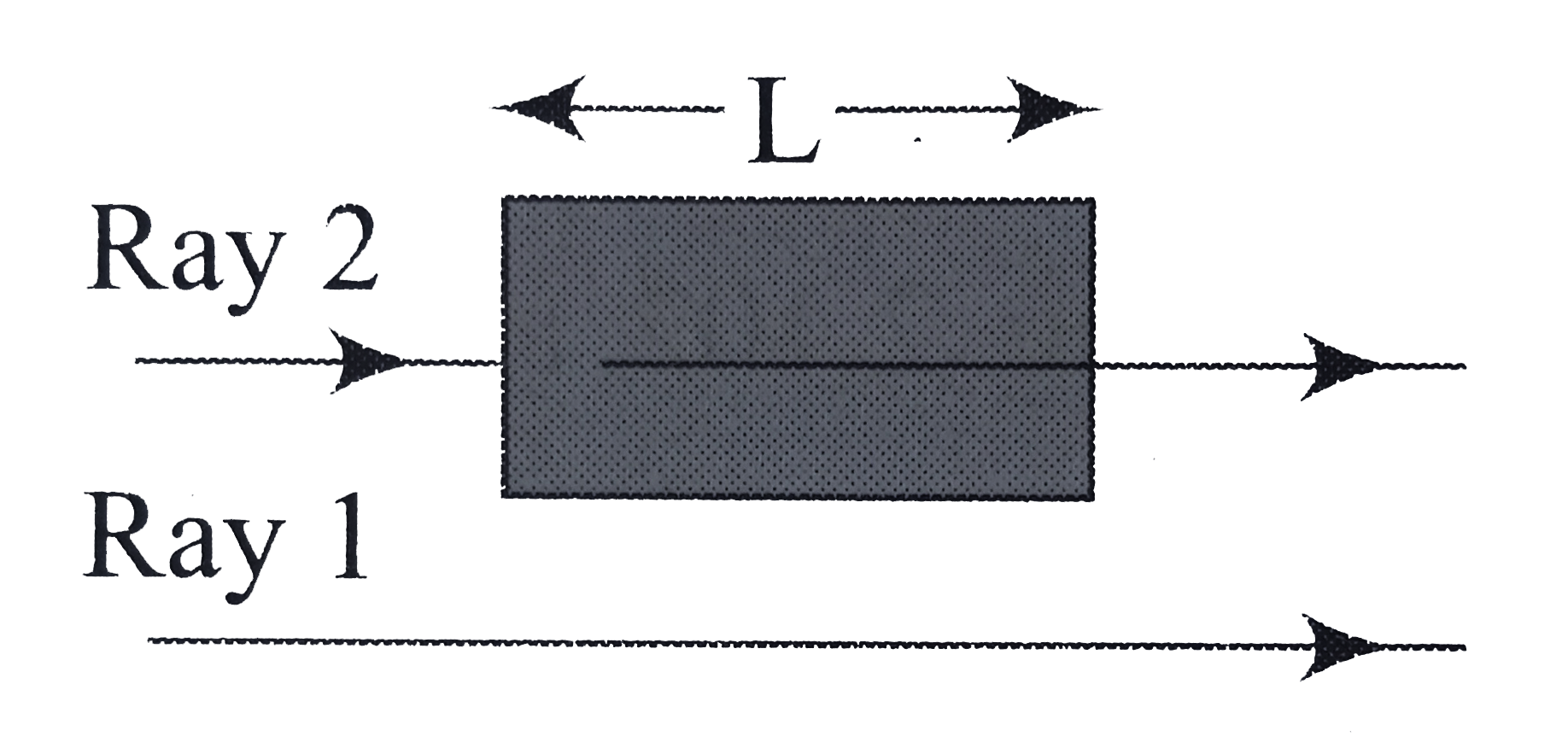
View SolutionIf the distance between the first maxima and fifth minima of a double-slit pattern is 7 mm and the slits are separated by 0.15 mm with the screen 50 cm from the slits, then wavelength of the light used is
View SolutionIn YDSE, `D = 1 m, d = 1 mm`, and `lambda = 5000 nm`. The distance of the 100th maxima from the central maxima is
View SolutionLet `S_(1)` and `S_(2)` be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle `/_ S_(1) P S_(2) = theta`, then fringe width for the light of wavelength `lambda` will be (assume `theta` to be a small angle)
View SolutionFigure shows two coherent sources `S_(1)-S_(2)` vibrating in same phase. `AB` is an irregular wire lying at a far distance from the sources `S_(1)` and `S_(2)`. Let `(lamda)/d=10^(-3)m,/_BOA=0.12^(@)`. How many bright spots will be seen on the wire, including points `A` and `B`

View SolutionThe path difference between two interfering waves at a point on the screen is `lambda // 6`, The ratio of intensity at this point and that at the central bright fringe will be (assume that intensity due to each slit is same)
View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index `n_(1)`. The wavelength of light in this medium is `lambda_(1)`. A transparent of thickness t and refractive index `n_(3)` is put in front of one slit. The medium between the screen and the plane of the slits is `n_(2)`. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
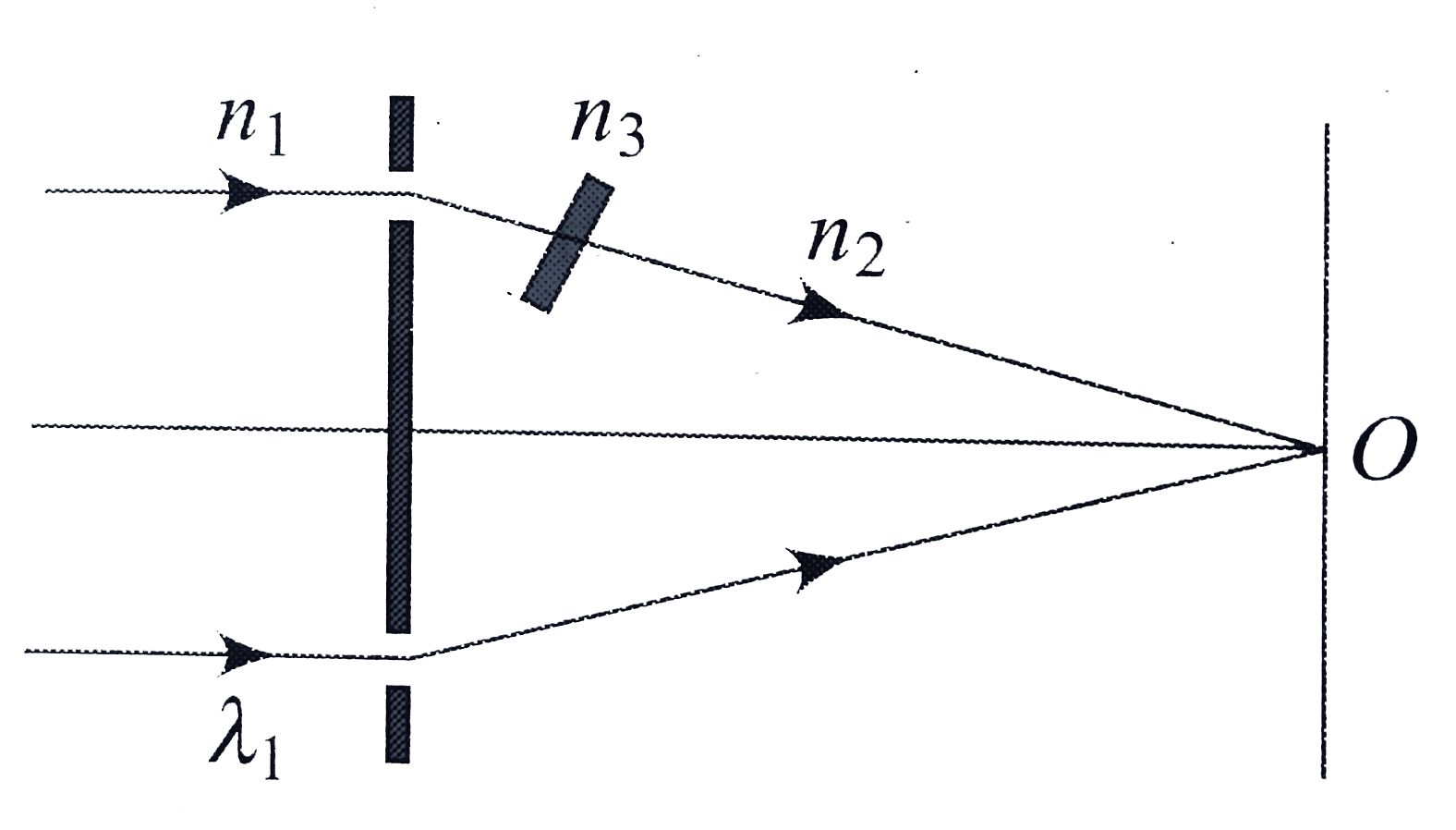
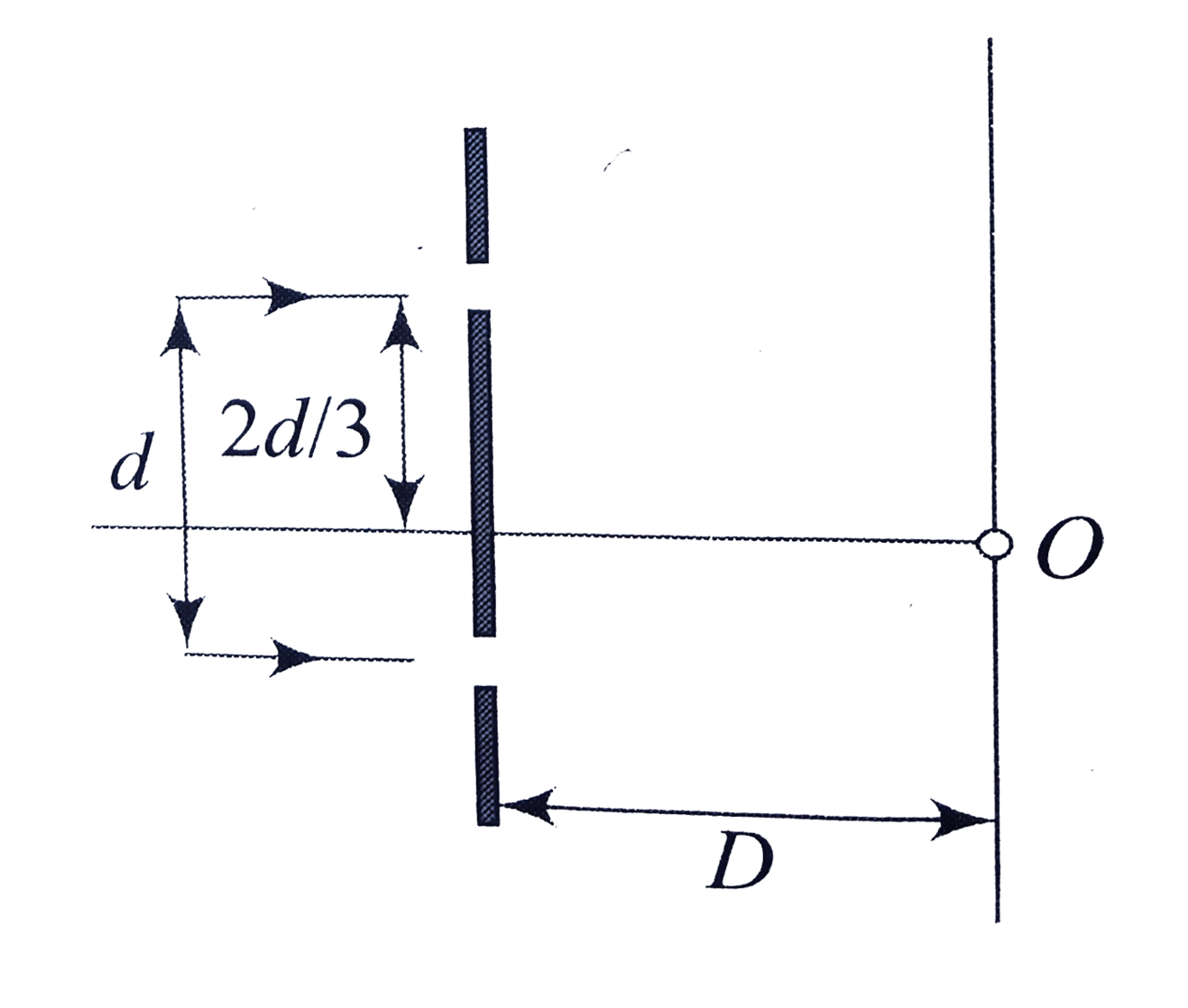
View SolutionIn figure, if a parallel beam of white light is incident on the plane of the slit, then the distance of the nearest white spot on the screen form O is [assume `d lt lt D, lambda lt lt D`]
View SolutionIn figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit `S_(1)` passes through a medium of variable refractive index `mu = 1 + ax` (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on `S_(1)`. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength `lambda` in air) is
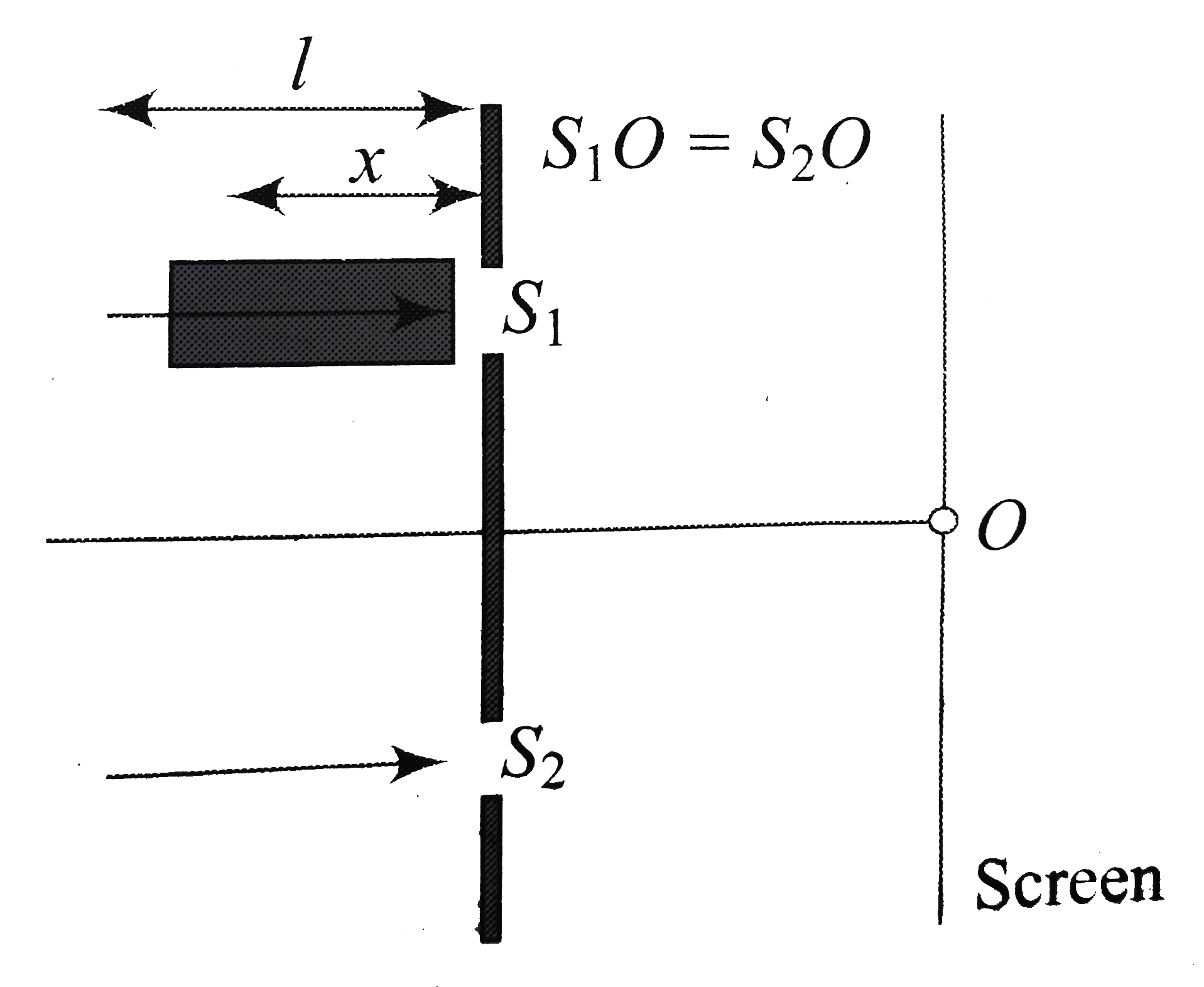
View SolutionInterference fringes were produced using light in a doulbe-slit experiment. When a mica sheet of uniform thickness and refractive index 1.6 (relative to air) is placed in the path of light from one of the slits, the central fringe moves through some distance. This distance is equal to the width of 30 interference bands if light of wavelength 4800 is used. The thickness (in `mu m`) of mica is
View SolutionTwo coherent light sources, each of wavelength `lambda`, are separated by a distance `3 lambda`, The maximum number of minima formed on line AB, which funs from `-oo` to `+oo`, is

View Solution`M_(1)` and `M_(2)` are plane mirrors and kept parallel to each other. At point O, there will be a maxima for wavelength `lambda`. Light from a monochromatic sources S of wavelength `lambda` is not reaching directly on the screen. Then, `lambda` is
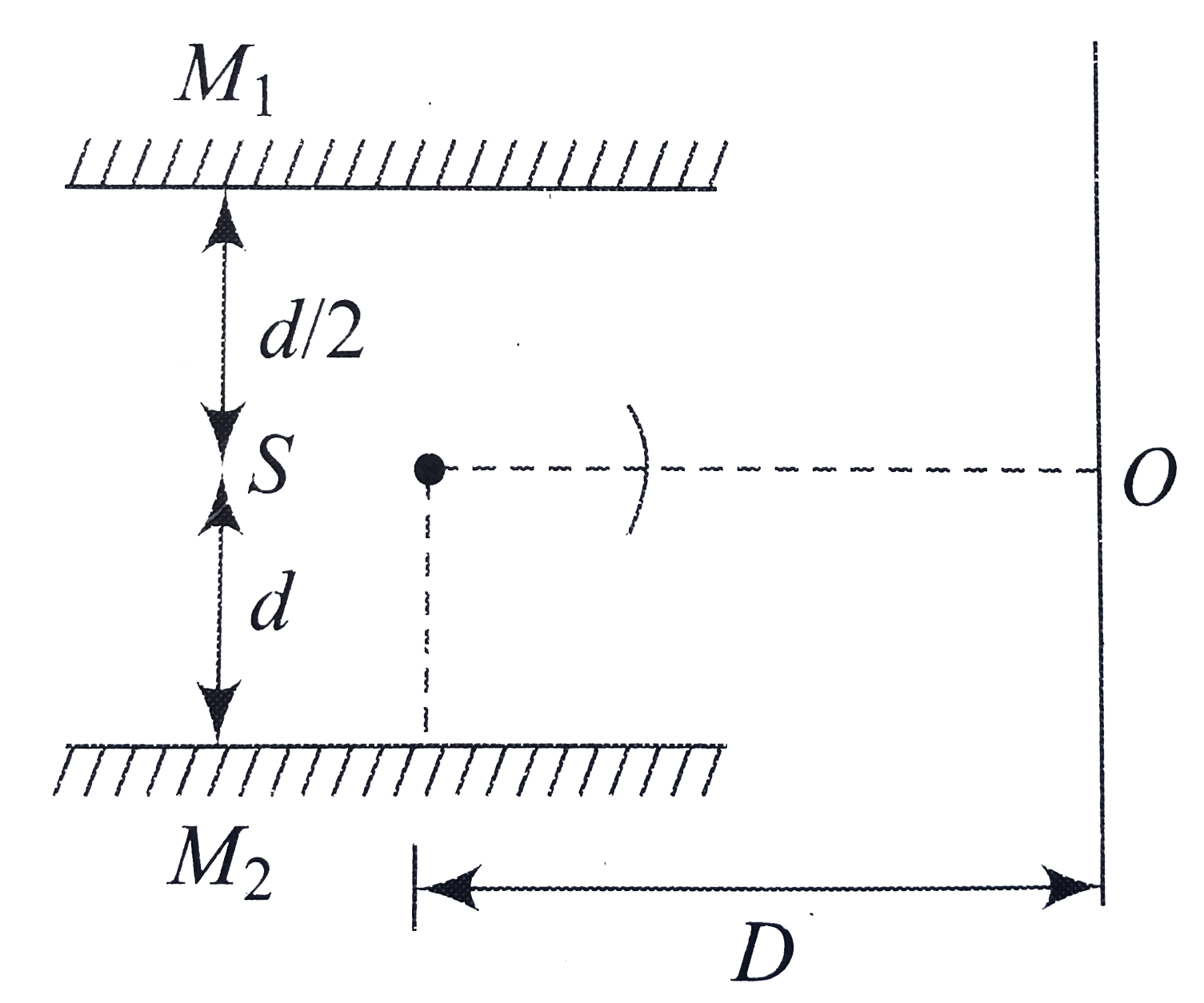
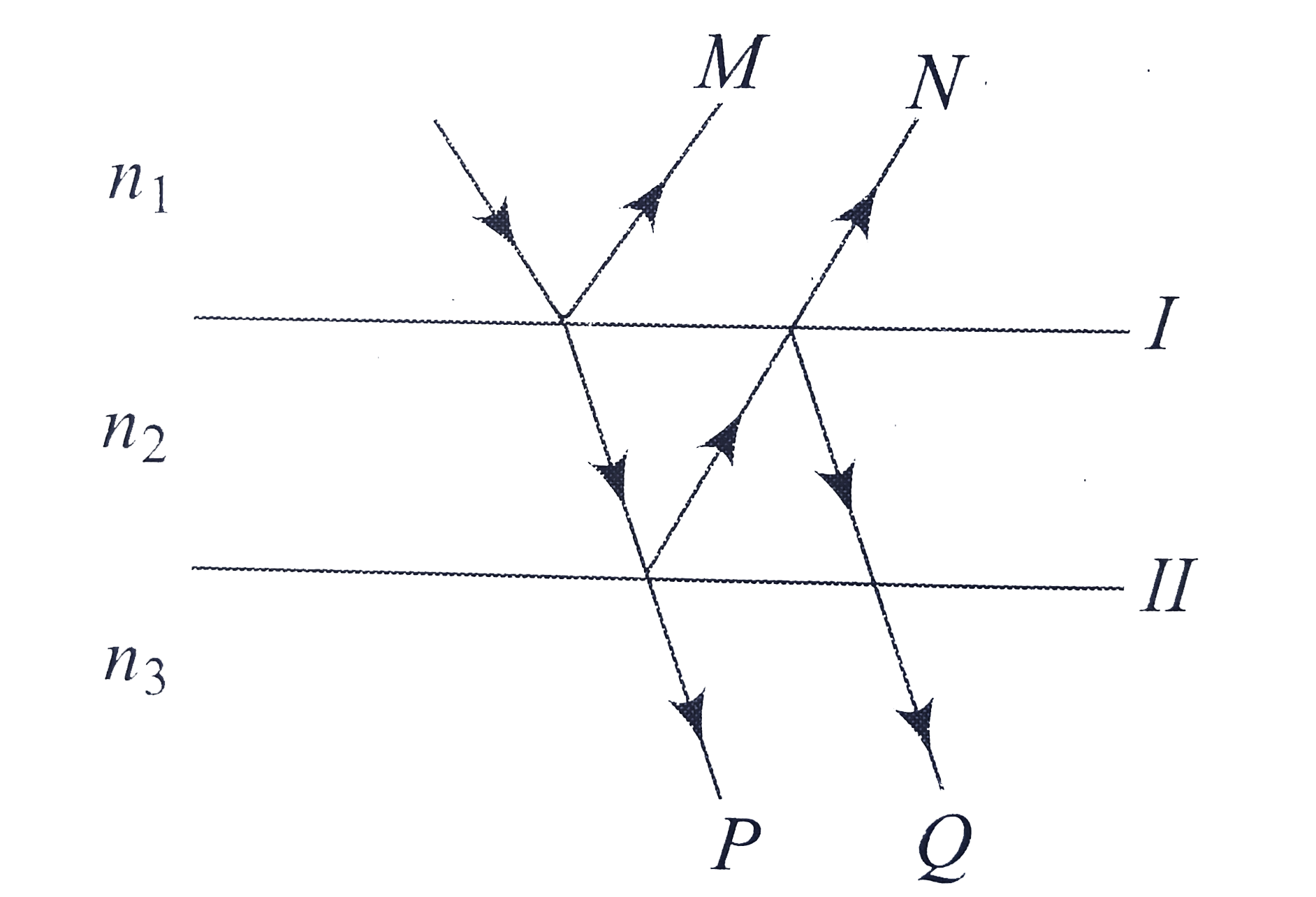
View SolutionA ray of light is incident on a thin film, As shown in figure, M and N two reflected rays while P and Q are two transmitted rays. Rays N and Q undergo a phase change of `pi`. Correct ordering of the refracting indices is
View SolutionIf one of the two slits of Young's double-slit experiment is painted so that it transmits half the light intensity as the second slit, then
View SolutionIn YDSE, coherent monochromatic light having wavelength 600 nm falls on the slits. First-order bright fringe is at 4.84 mm from central maxima. Determine the wavelength for which the first-order dark fringe will be observed at the same location on screen. `(Take D = 3 m.)`
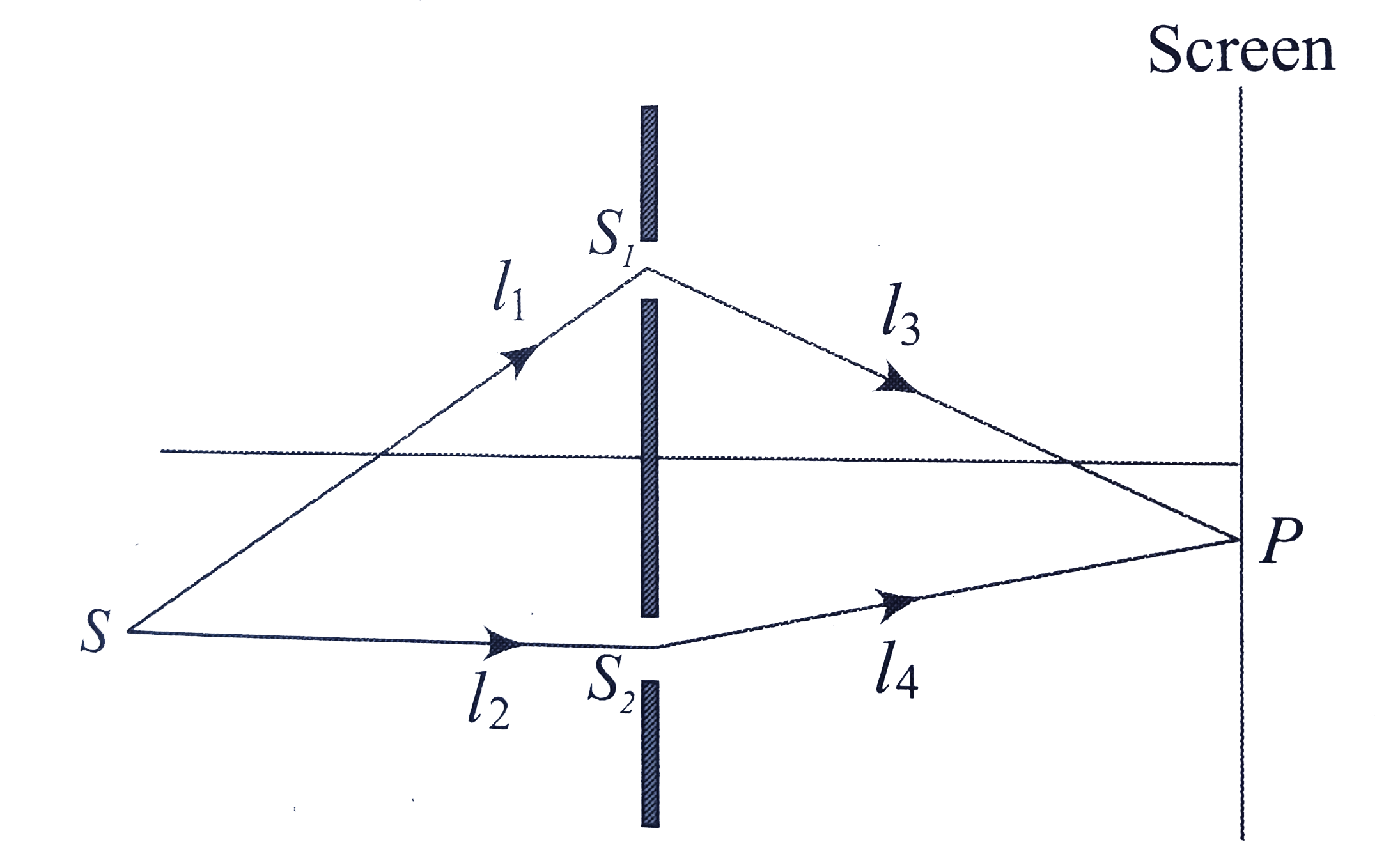
View SolutionThe YDSE apparatus is as shown in figure. The condition for point P to be a dark fringe is
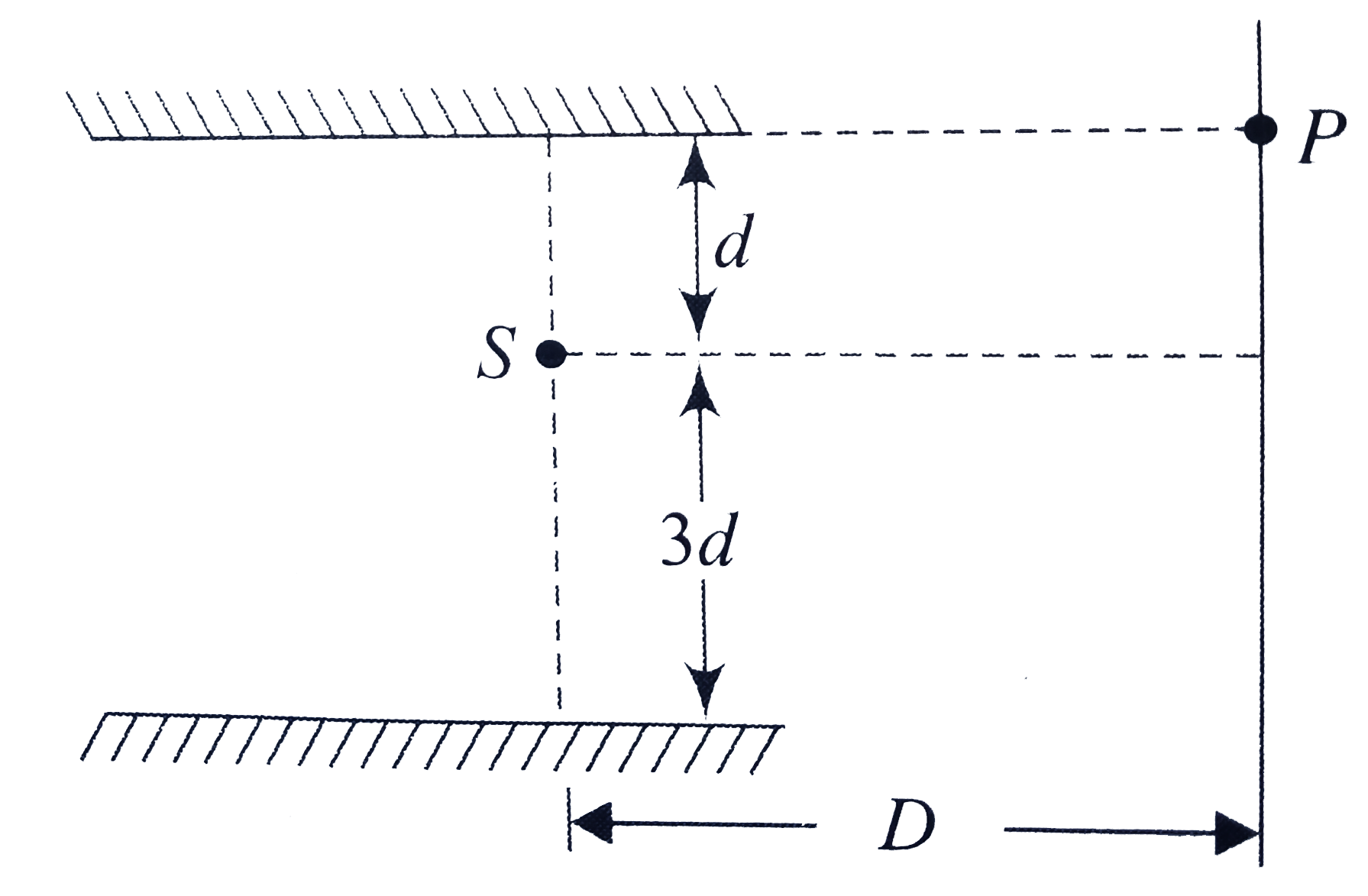
View SolutionConsider the optical system shown in figure. The point source of ligth S is having wavelength equal to `lambda`. The light is reaching screen only after reflection. For point P to be socond maxima, the value of `lambda` would be (`D gt gt d` and ` d gt gt lambda`)
View SolutionIn YDSE, if a bichromatic light having wavelengths `lambda_(1)` and `lambda_(2)` is used, then maxima due to both lights will overlaps at a certain distance y from the central maxima. Take separation between slits as d and distance between screen and slits as D. Then the value of y will be
View SolutionIn YDSE, `D = 2 mm, D = 2 m,` and `lambda = 500 nm`. If intensities of two slits are `I_(0)` and `9I_(0)`, then find intensity at `y = (1)/(6) mm`.
View SolutionIn YDSE, let A and B be two slits. Films of thickness `t_(A)` and `t_(B)` and refractive `mu_(A)` and `mu_(B)` are placed in front of A and B, respectively. If `mu_(A) t_(A) = mu_(A) t_(B)`, then the central maxima will
View SolutionIn YDSE, find the missing wavelength at `y = d`, where symbols have their usual meaning `(take Dgt gt d)`.
View SolutionIn YDSE, the amplitude of intensity variation fo the two sources is found to be `5%` of the average intensity. The ratio of the intensities of two interfering sources is
View SolutionIn YDSE, water is filled in the space between the slits and screen. Then
View SolutionIn YDSE, having slits of equal width, let `beta` be the fringe width and `I_(0)` be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be
View SolutionTwo identical coherent sources of wavelength `lambda` are placed at `(100 lambda, 0)` and `(-50 lambda, 0)` along x-axis. The number of maxima and minima detected are ,respectively [include origin and `(5 lambda, 0)]`
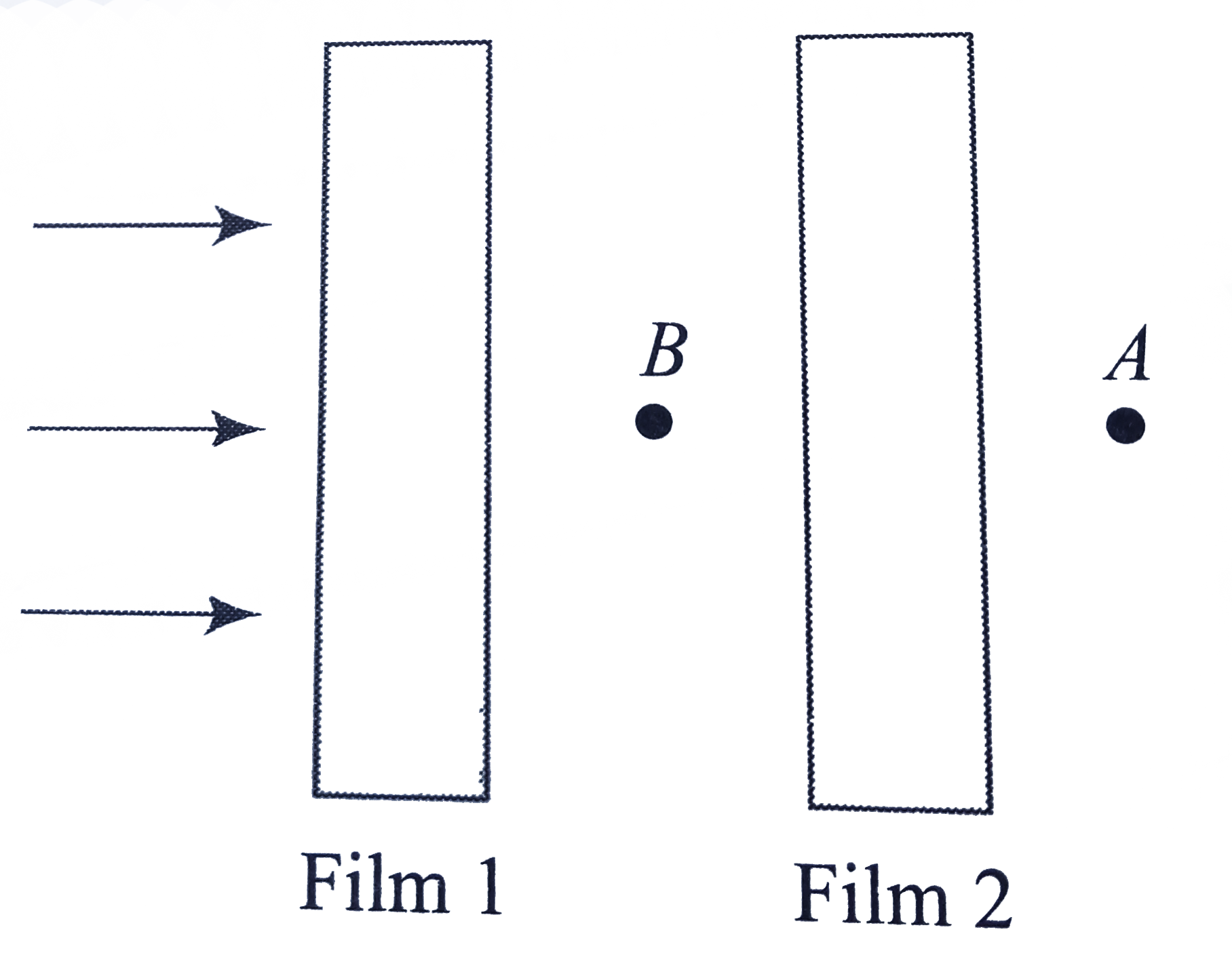
View SolutionTwo thin films of the same material but different thickness are separated by air. Monochormatic light is incident on the first film. When viewed normally form point A, the second film appears dark.
View SolutionConsider an YDSE that has different slit width. As a result, amplitude of waves from two slits are A and 2A, respectively. If `I_(0)` be the maximum intensity of the interference pattern, then intensity of the pattern at a point where phase difference between waves is `phi` is
View SolutionIn YDSE of equal width slits, if intensity at the center of screen is `I_(0)`, then intensity at a distance of `beta // 4` from the central maxima is
View SolutionTwo transparent slabs have the same thickness as shown in figure. One in made of material A of refractive index 1.5. The other is made of two materilas B and C with thickness in the ratio 1:2. The refractive index of C is 1.6. If a monochromatic parallel beam passing through the slabs has the same number of wavelengths inside both, the refractive index of B is

View SolutionLight of wavelength `lambda_(0)` in air enters a medium of refractive index n. If two points A and B in this medium lie along the path of this light at a distance x, then phase difference `phi_(0)` between these two point is
View SolutionIn a Young's double slit experiment, the slits are `2mm` apart and are illuminated with a mixture of two wavelength `lambda_0=750nm` and `lambda=900nm`. The minimum distance from the common central bright fringe on a screen `2m` from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other is
View SolutionIn Young's interference experiment, if the slit are of unequal width, then
View SolutionTwo wavelengths of light `lambda_(1)` and `lambda_(2)` and sent through Young's double-slit apparatus simultaneously. If the third-order bright fringe coincides with the fourth-order bright fringe, then
View SolutionIn Young's interference experiment, the central bright fringe can be indentified due to the fact that it
View SolutionA flake of glass (refractive index 1.5) is placed over one of the opening of a double-slit apparatus. The interference pattern displaced itself through seven successive maxima toward the side where the flake is placed. If wavelength of the light is `lambda = 600 nm`, then the thickness of the flake is
View SolutionTwo identical sources each of intensity `I_(0)` have a separation `d = lambda // 8`, where `lambda` is the wavelength of the waves emitted by either source. The phase difference of the sources is `pi // 4` The intensity distribution `I(theta)` in the radiation field as a function of `theta` Which specifies the direction from the sources to the distant observation point P is given by
View SolutionIn a double slit experiment instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
View Solution
Single Correct questions and complete solutions for chapter WAVE OPTICS of CENGAGE PHYSICS (HINGLISH) of Class 12