Complete Solutions to Comprehension Type of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| CENGAGE PHYSICS DPP | Comprehension Type |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
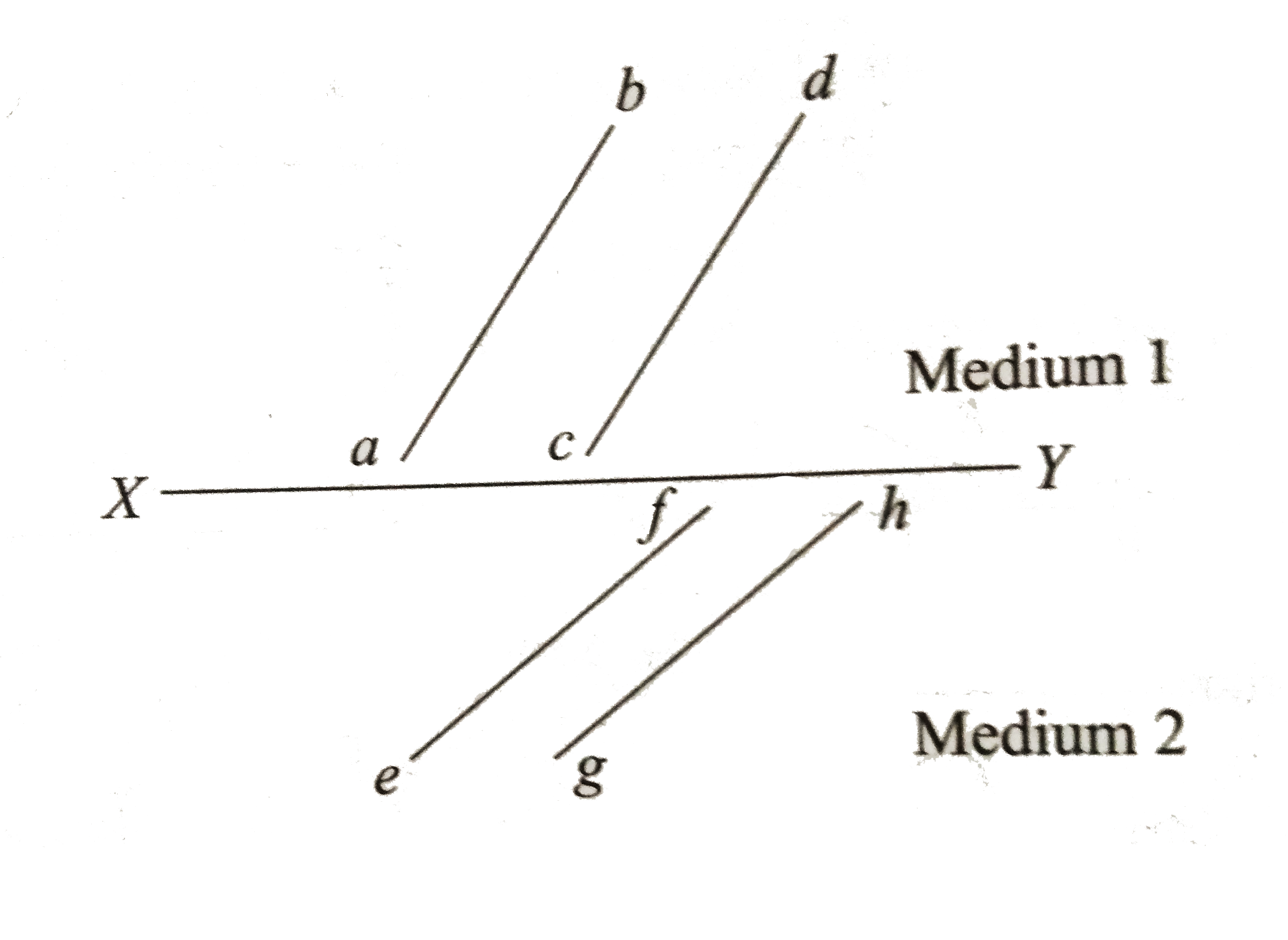
Fig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.

Light travel as a
View SolutionFig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.

The phase of the ligth wave at c, d, e, and f are `phi_(c)`, phi_(d), `phi_(e)` and `phi_(f)`, respectively. It is given that `phi_(c ) != phi_(f)`. Then
View SolutionFig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.
 Speed of light is
Speed of light is
View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at `S.S_(1)` and `S_(2)` are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from `S_(1) and S_(2)`. P is a point on the screen 1 mm from O at which path difference between waves from `S_(1) and S_(2)` is 11250Å. Position of amy point on the screen can be expressed by `theta`. The path difference is zero at O and a central bright fringe of intensity `I_(0)` is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is `(1)/(90)` radian. Answer the following question [assume D to be large and `theta` very small so taht `sinapproxtantheta approxtheta`]
Q. When the screen is at position (1), phase difference of waves from `S_(1)` and `S_(2)` at point P is effectively.

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at `S.S_(1)` and `S_(2)` are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from `S_(1) and S_(2)`. P is a point on the screen 1 mm from O at which path difference between waves from `S_(1) and S_(2)` is 11250Å. Position of amy point on the screen can be expressed by `theta`. The path difference is zero at O and a central bright fringe of intensity `I_(0)` is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is `(1)/(90)` radian. Answer the following question [assume D to be large and `theta` very small so taht `sinapproxtantheta approxtheta`]
Q. Intensity at P when the screen is at positio (1), is

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at `S.S_(1)` and `S_(2)` are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from `S_(1) and S_(2)`. P is a point on the screen 1 mm from O at which path difference between waves from `S_(1) and S_(2)` is 11250Å. Position of amy point on the screen can be expressed by `theta`. The path difference is zero at O and a central bright fringe of intensity `I_(0)` is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is `(1)/(90)` radian. Answer the following question [assume D to be large and `theta` very small so taht `sinapproxtantheta approxtheta`]
Q. Fringe width when screen is at position (1) will be

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at `S.S_(1)` and `S_(2)` are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from `S_(1) and S_(2)`. P is a point on the screen 1 mm from O at which path difference between waves from `S_(1) and S_(2)` is 11250Å. Position of amy point on the screen can be expressed by `theta`. The path difference is zero at O and a central bright fringe of intensity `I_(0)` is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is `(1)/(90)` radian. Answer the following question [assume D to be large and `theta` very small so taht `sinapproxtantheta approxtheta`]
Q. Intensity at point Q when screen is at position (1) is

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at `S.S_(1)` and `S_(2)` are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from `S_(1) and S_(2)`. P is a point on the screen 1 mm from O at which path difference between waves from `S_(1) and S_(2)` is 11250Å. Position of amy point on the screen can be expressed by `theta`. The path difference is zero at O and a central bright fringe of intensity `I_(0)` is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is `(1)/(90)` radian. Answer the following question [assume D to be large and `theta` very small so taht `sinapproxtantheta approxtheta`]
Q. Distance d between `S_(1) and S_(2)` is

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at `S.S_(1)` and `S_(2)` are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from `S_(1) and S_(2)`. P is a point on the screen 1 mm from O at which path difference between waves from `S_(1) and S_(2)` is 11250Å. Position of amy point on the screen can be expressed by `theta`. The path difference is zero at O and a central bright fringe of intensity `I_(0)` is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is `(1)/(90)` radian. Answer the following question [assume D to be large and `theta` very small so taht `sinapproxtantheta approxtheta`]
Q. When the screen is at position (2), its distance from the double slits is nearly

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at `S.S_(1)` and `S_(2)` are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from `S_(1) and S_(2)`. P is a point on the screen 1 mm from O at which path difference between waves from `S_(1) and S_(2)` is 11250Å. Position of amy point on the screen can be expressed by `theta`. The path difference is zero at O and a central bright fringe of intensity `I_(0)` is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is `(1)/(90)` radian. Answer the following question [assume D to be large and `theta` very small so taht `sinapproxtantheta approxtheta`]
Q. Angular position of a bright fringe of order 5 when the screen is at position (1), will be nearly

View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the shape of interference fringes on the screen?

View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the percentage intensity of the reflected light to the intensity of the reflectd light to the intensity of incident light?

View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. If the intensity of P correspoonds to a maximum, calculate the minimum distance through which the reflecting surface AB should so that intensity at P again becomes maximum.

View SolutionA YDSE is performed in a medium of refractive index `4 // 3`, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit `S_(2)` is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index `4 // 3`, ignore absorption.)
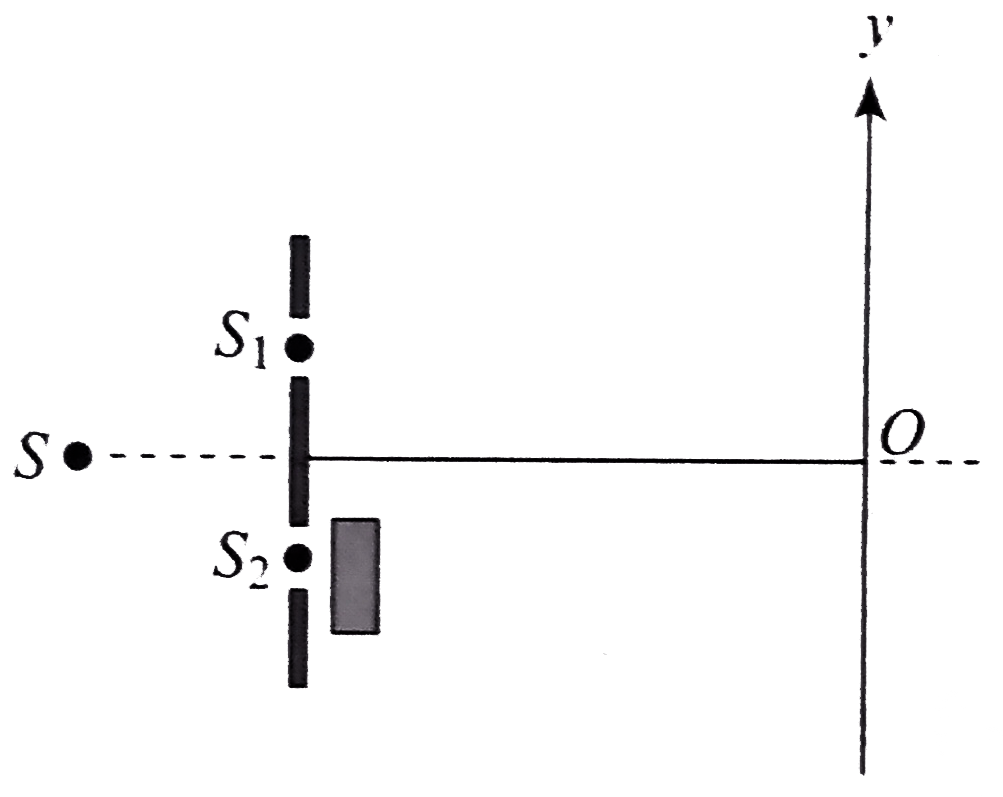
The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
View SolutionA YDSE is performed in a medium of refractive index `4 // 3`, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit `S_(2)` is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index `4 // 3`, ignore absorption.)

Find the light intensity at point O relative t maximum fringe intensity.
View SolutionIn YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit `S_(2)` is covered by a thin glass sheet of thickness 10.4`mum` and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:

View Solution
Comprehension Type questions and complete solutions for chapter WAVE OPTICS of CENGAGE PHYSICS (HINGLISH) of Class 12